Anton Rize

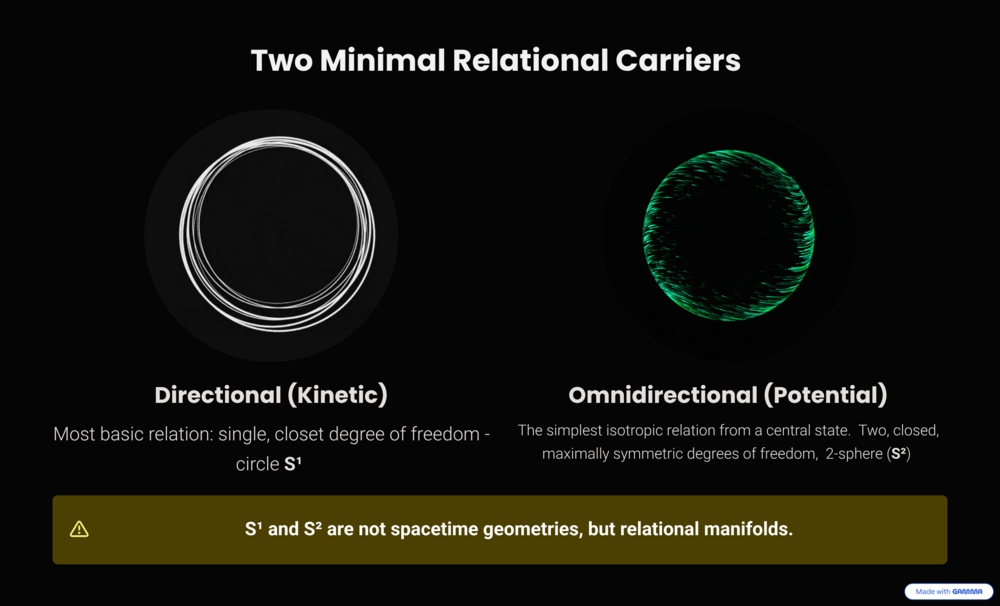
I really appreciate that, @studiot . It’s encouraging to see someone open to exploring new formulations. The S² projection is indeed the gravitational analogue of the same closure logic — I’ll outline it briefly below so you can see how it parallels the S¹ derivation: Potential Energy Projection on S² (SI Formulation) (Important note) S¹ and S² are relational manifolds of conservation, not physical spacetime surfaces. They describe how a single energy resource divides between two complementary projections - internal (phase) and external (amplitude). 1. Relational Conservation on S²The components  κₓ — internal (phase) projection  κᵧ — external (amplitude) projection obey  κₓ² + κᵧ² = 1. An increase in κᵧ corresponds to a higher gravitational potential (external relation), and a decrease in κₓ reflects contraction of proper length and slowing of proper time. These geometric redistributions generate all known gravitational effects. 2. Gravitational Tangent FormulationAnalogous to the SR relation using β = v / c, we define for the gravitational case:  κ = vₑ / c  where vₑ = √(2GM / r) is the escape velocity. Thus, κ is a dimensionless gravitational ratio, and κₓ = √(1 − κ²) defines the internal projection. (a) Kinematic relation (S¹)β = v / c = cos θ₁ E = E₀ / sin θ₁  p = (E₀ / c) cot θ₁  → E² = (p c)² + (E₀)² where E is total energy (J), E₀ = m c² (J), p is momentum (kg·m/s). (b) Gravitational relation (S²)κ = sin θ₂  κₓ = cos θ₂ E_g = E₀ / κₓ  p_g = (E₀ / c) tan θ₂  → E_g² = (p_g c)² + (E₀)² Both have the same invariant structure once dimensions are restored. 3. Unified InterpretationSR circle: (E βᵧ = E₀) with (β, βᵧ) = (cos θ₁, sin θ₁) GR circle: (E_g κₓ = E₀) with (κₓ, κ) = (cos θ₂, sin θ₂) Therefore:  E² = (p c)² + (m c²)²  E_g² = (p_g c)² + (m c²)² and  β ↔ κ,  cot θ₁ ↔ tan θ₂. Summary (SI-consistent): All physical quantities retain their standard dimensions:  [c] = m · s⁻¹  [m] = kg  [E] = J = kg · m² · s⁻²  [p] = kg · m · s⁻¹. Relativistic and gravitational relations are duals - two geometric projections of the same conserved quantity E₀ = m c². If you interested in the next post I’ll show how their composition leads directly to the Equivalence Principle, where m_g = m_i appears not as a postulate but as a geometric identity. Hilbert’s variational principle is an elegant route to GR - but it relies on an external time parameter and a freedom to vary trajectories. In the relational framework, both of these assumptions dissolve naturally: change itself defines the temporal order. I’ll show later how this leads to a reformulation of dynamics without equations of motion - a purely geometric self-consistency where energy redistribution replaces the action principle. Its quite fascinating.

@studiot There are two notational layers. In natural units (c = 1) the mass shell is E² = p² + m², (c = 1) and in SI (or any dimensional system) the same statement is E² = (p·c)² + (m·c²)². (SI units) If you want to substitute SI units, use the dimensional form above. Nothing is dimensionally incorrect there. For completeness, the projections used in the derivation are: β := v/c, β_Y := √(1 − β²) E = E₀ / β_Y, with E₀ := m·c² p·c = E₀ · (β / β_Y) ⇒ p = (E₀/c) · (β/β_Y) = γ m v Check: (p·c)² + (m·c²)² = [E₀·(β/β_Y)]² + E₀² = E₀²[(β²/β_Y²) + 1] = E₀²[(β² + β_Y²)/β_Y²] = E₀²/β_Y² = (E₀/β_Y)² = E². Units (SI) for bookkeeping: [c] = m·s⁻¹, [m] = kg, [E] = J = kg·m²·s⁻², [p] = kg·m·s⁻¹, [v] = m·s⁻¹. So: substitute your SI values into E² = (p·c)² + (m·c²)². The shorter E² = p² + m² line I quoted earlier was in c = 1 notation only. But this is really just the tip of the iceberg. The same geometric logic extends beautifully to gravity through the S² projection - that’s where the equivalence principle and curvature emerge directly from the same closure rules. If you’d like, I can show that next - it’s quite elegant and completes the SR/GR connection without introducing tensors.

The interesting thing is that in RG, all primary quantities (β, κ, τ, Q etc.) are dimensionless by construction. It operates entirely through normalized relational ratios, not dimensional measures. That means the equations remain valid under any consistent unit system - SI, Planck, geometrized, or even a hypothetical alien metric. As long as their constants are internally consistent, the relational structure behaves identically. This scale-independence is deliberate: it reflects the idea that physics should describe relations rather than magnitudes. Units are a linguistic layer - the grammar of measurement, not the content of reality. For numerical predictions or comparison with empirical data, it’s always practical to restore SI units for bookkeeping: • [c] = m·s⁻¹ • [m] = kg • [E] = J = kg·m²·s⁻² • [p] = kg·m·s⁻¹ • [v] = m·s⁻¹ Nothing unconventional here - all formulas reduce to standard dimensional identities once SI is restored. I must admit I didn’t expect the discussion to turn to unit conventions - I was hoping for comments on the derivation I posted earlier. The structure itself is what matters; units are just the language we use to read it.

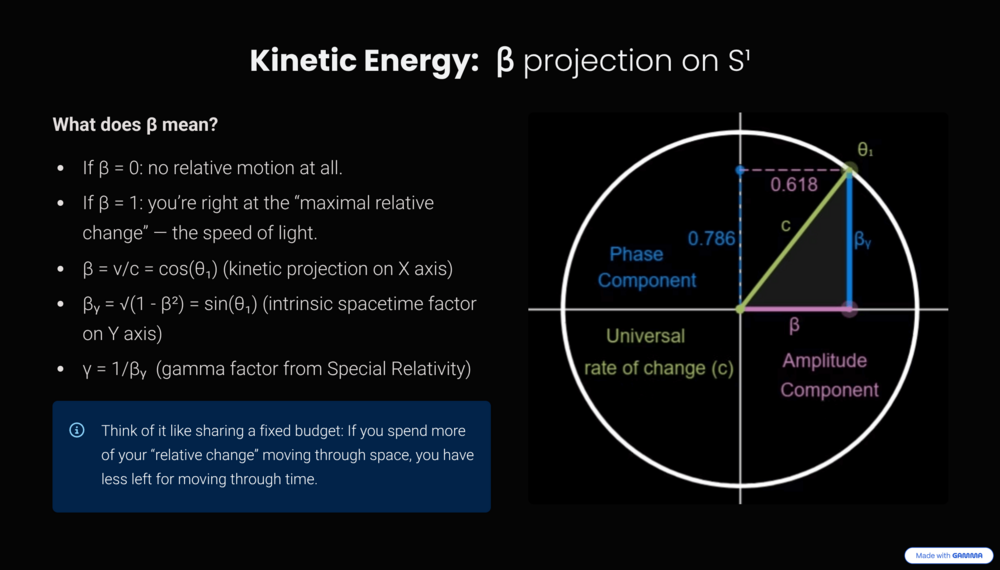
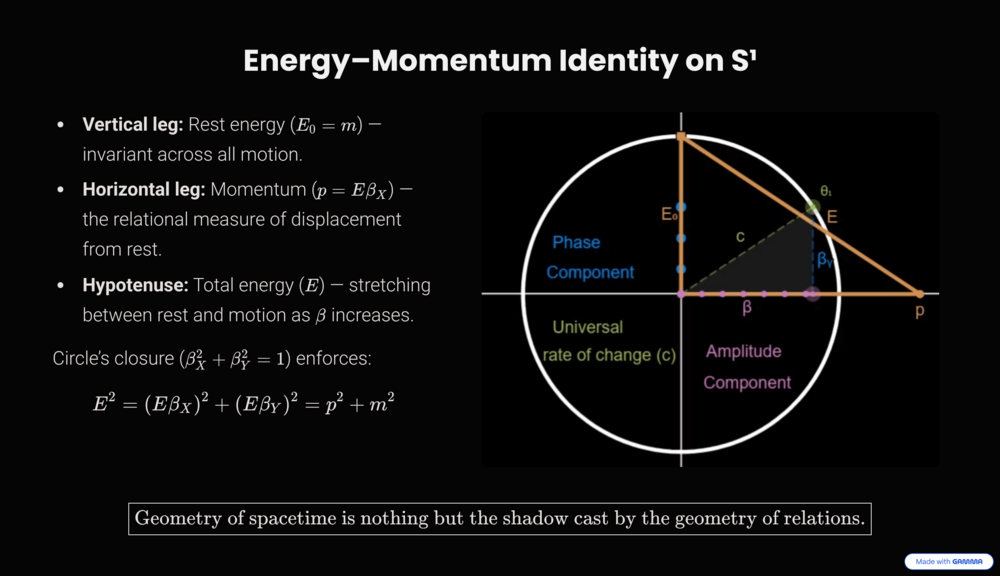
Thank you, noted. Here’s the formal glossary for clarity, as all quantities are defined geometrically within the relational circle: E – total energy of the closed relational system E₀ – invariant rest energy (vertical projection of E) p – momentum (horizontal projection of E) m – rest mass, identical to E₀ in c = 1 normalization βₓ, βᵧ – normalized projections on S¹, satisfying βₓ² + βᵧ² = 1 θ₁ – angular coordinate on S¹, βₓ = cos θ₁, βᵧ = sin θ₁ KINETIC ENERGY PROJECTION ON S¹ Since S¹ encodes one-dimensional displacement, the total energy E of the system must project consistently onto both axes: Eₓ = E·βₓ , Eᵧ = E·βᵧ. THEOREM - Invariant Projection of Rest Energy: For any state (βₓ, βᵧ) on the relational circle, the vertical projection of the total energy is invariant: E·βᵧ = E₀. PROOF: When βₓ = 0, closure enforces βᵧ = 1, yielding E = E₀. Since closure applies for all θ₁, the vertical projection E·βᵧ remains equal to this rest value in every state. COROLLARY - Total Energy Relation: E = E₀ / βᵧ = E₀ / √(1 − βₓ²) REMARK - Lorentz Factor: The historical Lorentz factor γ is simply 1 / βᵧ. No additional structure is introduced: all content is already present in E·βᵧ = E₀. SUMMARY: γ = 1 / βᵧ. REST ENERGY AND MASS EQUIVALENCE Within normalization c = 1, the invariant rest energy equals mass: E₀ = m. PROOF: From the invariant projection E·βᵧ = E₀ and closure of S¹, no additional scaling parameter is required. Hence conventional bookkeeping identities E₀ = m·c² or m = E₀ / c² reduce to tautologies. Mass is therefore not independent, but the rest-energy invariant itself. REMARK: In a framework that is genuinely fundamental and free from arbitrary human units, the natural normalization is always c = 1. With this normalization, the identities E₀ = m·c² or m = E₀ / c² lose all significance. They collapse into the only consistent statement: E₀ = m. Thus mass is the invariant projection of total rest energy. ENERGY–MOMENTUM RELATION PROPOSITION - Horizontal Projection as Momentum: On the relational circle, the unique relational measure of displacement from rest is the horizontal projection E·βₓ; hence p ≡ E·βₓ (c = 1). PROOF: The rest state is (βₓ, βᵧ) = (0, 1). A displacement measure must (i) vanish at rest, (ii) grow monotonically with |βₓ|, and (iii) flip sign under βₓ → −βₓ. The only relational candidate satisfying (i)–(iii) is E·βₓ. Thus the identification is necessary rather than conventional. COROLLARY - Energy–Momentum Relation: With p identified by the previous definition and m = E₀, the closure identity yields E² = p² + m² (c = 1). Equivalently, restoring c: E² = (p·c)² + (m·c²)². PROOF: By closure, (E·βₓ)² + (E·βᵧ)² = E². Substituting p = E·βₓ and m = E₀ proves the claim. Restoring c is dimensional bookkeeping: p → p·c and m → m·c², while E remains E, yielding the standard form. REMARK - Geometric Forms: E² = ( (βₓ / βᵧ)·E₀ )² + E₀² = ( cot(θ₁)·E₀ )² + E₀². These are equivalent renderings of the same geometric necessity. REMARK - Units sanity check (bookkeeping): Using βₓ = v/c, the identification p ≡ E·βₓ gives p·c = E·(v/c) ⇒ p = (E·v) / c². With E = (1/βᵧ)·m·c² = γ·m·c², this reduces to p = (βₓ/βᵧ)·m·c = γ·m·v, the standard relativistic momentum. No new parameters introduced. TABLE - Representation of relativistic effects: βₓ = β , β = v/c , θ₁ = arccos(β) Algebraic form: 1/βᵧ = 1/√(1−β²) = 1/√(1−(v/c)²) βᵧ = √(1−β²) = √(1−(v/c)²) Trigonometric form: 1/βᵧ = 1/sin(θ₁) = 1/sin(arccos(β)) βᵧ = sin(θ₁) = sin(arccos(β)) SUMMARY: The energy–momentum relation E² = p² + m² is a geometric identity of S¹. If you’re interested, next I can show how the same logic extends from the kinetic S¹ projection to the gravitational S² projection, yielding the equivalence principle directly from symmetry. It’s quite elegant, and it closes the SR/GR bridge naturally.

@studiot @studiot Thanks. Let me address your points precisely and ask you to pinpoint the exact step you dispute. 1) “E² = p² + m² is derived but not as you said.” The derivation I gave uses only: (i) the circle identity βₓ² + βᵧ² = 1, (ii) E₀ ≡ E·βᵧ (rest-invariant projection), (iii) p ≡ E·βₓ (displacement projection). Then (E·βₓ)² + (E·βᵧ)² = E² ⇒ p² + E₀² = E². If you think this is illegitimate, please say which identification you reject: A) E₀ ≡ E·βᵧ, or B) p ≡ E·βₓ, or C) the use of βₓ²+βᵧ²=1. “Generally wrong” doesn’t help; name the line and I’ll fix it or show the algebra. 2) On Gμν = (8πG/c⁴)Tμν “not meaning spacetime = energy.” Agreed: the equation does not identify kinds. It states a structural constraint: curvature equals (constant)×stress-energy. My “≡” denotes ontological equivalence of descriptions (mutual definability), not sameness of substance. Your analogies “F = ma ⇒ force is mass”, “distance = speed×time ⇒ distance is time” actually make my point: equality of relations ≠ identity of categories. That’s exactly how I’m reading EFE. 3) “Spacetime is not even a real space.” Yes. And in WILL neither S¹ nor S² are treated as “real space”; they are bookkeeping manifolds enforcing closure/isotropy of a conserved relational resource. Ordinary spacetime is an emergent coordinate representation. So here we agree. 4) “Relational geometry” caricature and the sugar–honey–vinegar example. Composing arbitrary predicates (“sweet”, “brown”) has no algebra and no invariant - of course it doesn’t compose. RG, relations compose because they share a common invariant budget: • Kinematics: β²+βᵧ²=1, • Gravity: κₓ²+κ²=1, • Exchange (closed orbits): κ²=2β². Those are quadratic constraints with a well-defined composition law (projections on one conserved quantity). That is why A–B and B–C imply a determinate A–C. 5) “Tensorial equation quoted inappropriately.” Nothing inappropriate was inferred beyond what I’ve just clarified: EFE links geometry and energy-momentum by equality of relations, not by identity of entities. That’s exactly my usage. So the crux is simple: if you accept (i)–(iii) above, the mass shell follows as an identity. If you reject one of (i)–(iii), which one and why? Point me to the exact line you find unsound, and I’ll respond with the full derivation you prefer (metric, rapidity χ, or purely algebraic). Let me take a brief pause from the line-by-line debate to clarify what kind of question this discussion actually belongs to. What we are discussing here is not really whether one can write “spacetime ≡ energy” or which algebraic symbol is more proper. It is the continuation of a philosophical debate that began more than three centuries ago - between Newton’s substantivalism and Leibniz’s relationalism, later echoed in Mach and Einstein. Newton’s view: space and time exist as independent containers - an absolute background in which events unfold. Leibniz’s view: space and time are nothing over and above the relations among entities and their changes. General Relativity kept Newton’s mathematics but never fully escaped his ontology: spacetime in GR still exists even in the absence of matter (the vacuum solution). That is substantivalism in disguise - geometry treated as an independent thing. Einstein himself was never satisfied with this. In his later correspondence with Schilpp and Besso, he called GR “a provisional synthesis” and wrote explicitly that a truly Machian theory would eliminate spacetime as an independent entity altogether. RG continues that unfinished line - it is not a denial of GR, but the completion of Einstein’s own relational intent. Its principle (Structure ⇔ Dynamics) simply removes the last residue of substantivalism: geometry and energy are two projections of a single relational resource. So when someone objects that “spacetime = energy makes no sense,” they are unknowingly taking Newton’s side of the same 300-year-old debate. The question is not whether GR’s equations work - of course they do. The question is whether they describe the world as it is or a mathematical prosthesis that still carries Newton’s metaphysics. That is the level at which RG operates. Everything else - tensors, topology, units - follows from that one epistemic decision.

@ exchemist Ha! Good reference - though self-satisfied toasters could probably solve most of my philosophical dilemmas. I already posted the short version of this derivation earlier, but I’ll quote it again here for clarity: Let me know if any step seems unclear or if you’d like to see the full version. I’m happy to go through it line by line - that’s exactly what makes discussions like this valuable. Like all of you, I just want to get closer to the Truth, and the fastest path forward is by correcting mistakes; the slowest is by confirming biases. There’s no loss for me in this debate as long as I stay scientifically honest - to you guys, and most importantly, to myself.

@joigus Thanks for jumping in - appreciate the GR-specific angle. A few clarifications to address your points directly: First, on infographics: These aren't just visuals - they illustrate the logical flow of derivations (e.g., from ontological blind spot in separating structure/dynamics to constraints leading to S¹/S² carriers, then projections yielding identities like E² = p² + m²). They're backed by theorems/lemmas in the docs (e.g., Appendix I derives EFE as κ² = κ² identity). If they seem superficial, happy to post the equations here instead - let me know which part (e.g., Schwarzschild equivalence?). On EFE not saying "spacetime = energy": You're right - EFE (Gμν = (8πG/c⁴)Tμν) is a relation (curvature proportional to energy-momentum), not literal equality. But in WILL, "≡" is ontological equivalence: Structure (geometry) and dynamics (energy) are mutually defining aspects of one relational system, not separate. EFE emerges as the tt-component identity (G_tt ⇔ κ², T_tt ⇔ ρ), derived algebraically without metrics (see Appendix I: d/dr(κ² r) = (8πG/c²) r² ρ(r) → κ² = ρ/ρ_max). It's not a misreading - it's a reinterpretation resolving GR's substantival assumptions. Which brings me to the key: This debate is substantivalism (spacetime as independent substance) vs. relationalism (spacetime as emergent relations) - and it's very much open in physics/philosophy. Standard GR leans substantival (vacuum solutions imply independent spacetime), but Einstein himself saw it as relational (influenced by Mach's principle) and spent his later years trying to make GR fully Machian (no absolute effects; e.g., letters to Schilpp). Relational views (e.g., Barbour, Rovelli, Smolin) argue substantivalism adds unnecessary ontological burden (a "container" without content), while relationalism minimizes it (Occam's razor). Judging WILL from GR axioms embeds that burden circularly - it's a category error. Burden of proof: Substantivalists must justify the extra entity (independent spacetime), as relationalism explains the same data with less (e.g., WILL derives EFE, conserves energy relationally via ΔE_{A→B} + ΔE_{B→A} = 0 but globally redistributes via projections - no global non-conservation issue, as no independent arena). On energy in GR: Yes, not globally conserved in general metrics (no Killing vector), but WILL avoids this by making spacetime emergent - energy is conserved in relations (closures like κ²=2β²), with "loss" as phase redistribution (e.g., redshift/cosmo in Part II). It's a useful concept everywhere in WILL, not just local patches. If this line of reasoning makes sense, you can see the formal derivations on the website (https://antonrize.github.io/WILL/) or via the archived DOI (https://doi.org/10.5281/zenodo.17115270). Alternatively, if you'd prefer, I can post the algebraic sequence for a specific case right here - for example, how κ² = 2β² emerges from the angular relations. Open to any concrete test or line-by-line examination.

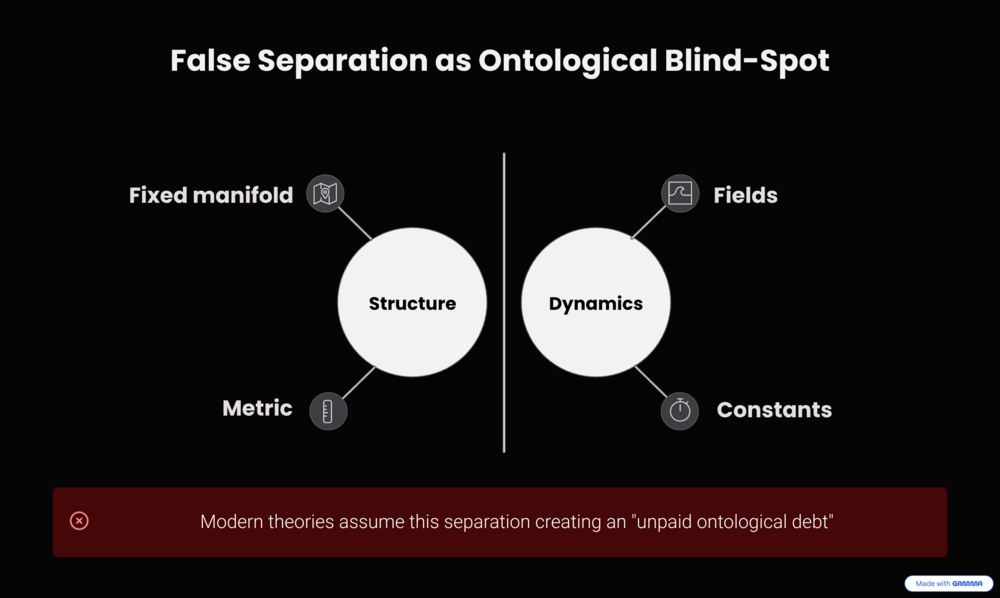
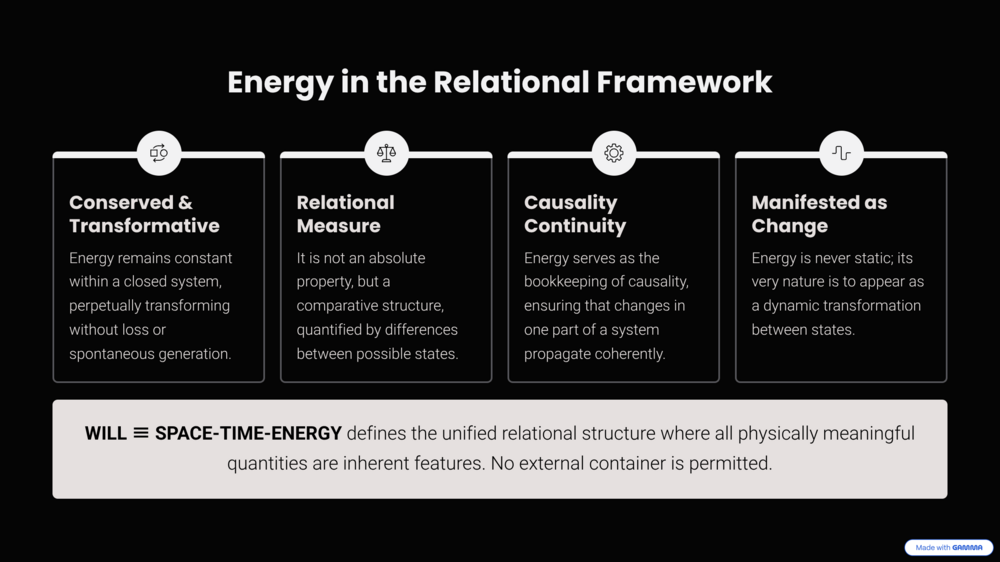
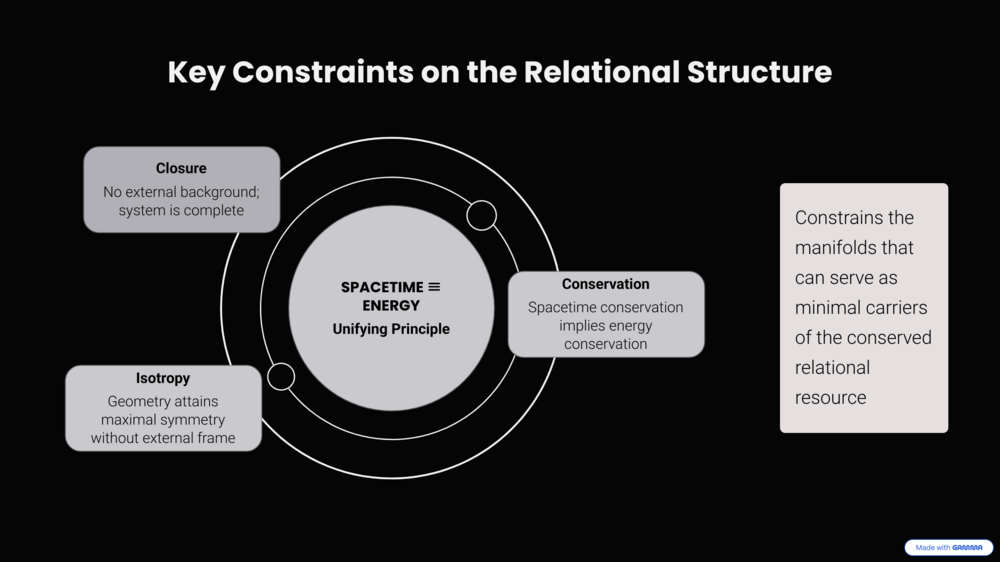
@studiot, thank you for the follow-up and the detailed critique. You've clearly articulated several key objections regarding: (1) the use of the '≡' symbol, (2) a perceived tautology (that the physics is "embedded" beforehand), and (3) a false association with other non-mathematical posts. These points clearly represent the core misunderstanding of the model's foundations, and I will address them in order. 1. On the notation “SPACETIME ≡ ENERGY” You are formally correct that “≡” denotes a mathematical identity, and I understand the discomfort. My choice of this symbol was deliberate, precisely because standard mathematics lacks a specific notation for “ontological equivalence” or “mutual definition” (at least as far as I know - if you can suggest a more accurate one, I’m open to it). The foundational principle (W1) is that “Spacetime” and “Energy” are not two separate entities that happen to interact; they are two perspectives on a single, self-consistent relational structure. What we perceive as spacetime geometry is the structure of energy relations. This leads directly to your second point. You wrote: “This is especially misleading as the terms energy and spacetime do not refer to identical entities, and there is no Physics or Mathematics in which they may be related by the equals sign either.” I must strongly object to this specific claim, as it is demonstrably incorrect. The very foundation of 20th-century physics is built on precisely such an equation: Gμν = (8πG / c⁴) Tμν On the Left-Hand Side (LHS): The Einstein tensor Gμν (Geometry / Spacetime). On the Right-Hand Side (RHS): The Stress-Energy tensor Tμν (Energy / Matter). This is the mathematical equation that directly relates spacetime geometry and energy distribution through the equals sign. Relational Geometry (RG) merely takes this established physical principle to its logical conclusion. As demonstrated in Appendix I, the geometric field equation is proven to be mathematically equivalent to the corresponding component of the Einstein Field Equations. Here is the derivation summarized from Appendix I: The standard form for the tt-component of Einstein’s field equations (one of the TOV equations) is: (1 / r²) d/dr [r (1 - 1/g_rr)] = (8πG / c²) * ρ(r) where g_rr (a component of spacetime geometry) is related to the enclosed energy m(r) by: 1 - 1/g_rr = 2Gm(r) / (r * c²) The RG defines its potential projection κ using this exact geometric term: κ²(r) ≡ 2Gm(r) / (r * c²) Substituting this definition into the EFE yields: (1 / r²) d/dr (r κ²(r)) = (8πG / c²) * ρ(r) which simplifies to the differential form of the RG field equation: d/dr (r κ²) = (8πG / c²) r² * ρ(r) Furthermore, RG defines energy density algebraically as ρ(r) = κ²(r) c² / (8πG r²). This leads to the central equivalence: κ²(r) = ρ(r) / ρ_max(r) As shown in the Appendix, differentiating this algebraic form confirms its consistency with the differential EFE form. Therefore, the apparent complexity of the Einstein Field Equation is mathematically equivalent to a simple algebraic identity: (EFE differential form) ⇔ (κ²(r) = ρ(r) / ρ_max(r)) ⇔ (κ² = κ²) This demonstrates that “SPACETIME ≡ ENERGY” is not a metaphysical claim but the underlying simplified algebraic reality already encoded within General Relativity. Therefore, my use of “≡” was intended to capture this fundamental equivalence - which is at the heart of modern physics - expressed in its most direct, algebraic form. 2. On the charge of “Tautology” (that the physics is already embedded)This is indeed your central objection, and it deserves a clear answer. You argue that the diagrams are meaningless because: and that I am merely “verifying the arithmetic.” That interpretation is not correct. The model is generative, not descriptive. Relational Geometry (RG) does not assume the E² = p² + m² relation - it derives it. Here is the explicit derivation. It follows a strictly logical sequence, beginning from only one methodological principle: 1. Methodological minimalism - we start with nothing beyond epistemic hygiene: a refusal to accept unjustified assumptions. 2. Identifying the ontological blind spot - applying this minimalism to modern physics reveals a hidden separation between “Structure” (the spacetime container) and “Dynamics” (the energy content). 3. Deriving the W₁ principle - removing this single unjustified separation forces the logical conclusion that Structure and Dynamics are mutually defining: Structure ⇔ Dynamics. This becomes the foundational principle (W₁), derived, not postulated. “WILL ≡ SPACETIME ≡ ENERGY” is the shorthand for this unified relational structure. All physically meaningful quantities are internal relations within WILL; no external container is permitted. 4. Derived constraints - from (W₁), three necessary conditions follow: • Closure: the system is self-contained - no external reservoir of “energy” exists. • Conservation: within WILL, the total relational transformation resource is conserved. • Isotropy: if no external background is allowed, no direction can be privileged; hence the relational geometry must be maximally symmetric. 5. Derivation of the carrier (S¹): applying minimalism again, the simplest possible closed 1D structure satisfying the closure condition is the circle S¹. 6. Geometric law: S¹ geometry has an intrinsic property - its projections obey the Pythagorean identity βₓ² + βᵧ² = 1. This is pure mathematics, not a physical assumption. 7. Physical identification: we now interpret these projections according to their invariant roles: • βᵧ → the component equal to 1 at rest corresponds to the rest invariant, E₀ = E·βᵧ. • βₓ → the component vanishing at rest corresponds to displacement, p = E·βₓ. 8. Generated theorem: substituting these identifications into the geometric identity gives: (E·βₓ)² + (E·βᵧ)² = E² ⇒ p² + E₀² = E² Thus, E² = p² + m² is not an assumption within the framework; it is a derived theorem. The physics of Special Relativity emerges as a necessary algebraic consequence of the derived geometry itself. 3. On the association with “similar non-mathematical proposals”You also compared this work to another post: (“The Fundamental Interrelationships Model”) and implied that the two share the same nature. With respect - that comparison is misplaced. The cited thread discusses a speculative synthesis of physics, biology, and sociology. It makes no quantitative claims, provides no mathematical derivations, and does not reproduce any empirical results. Its aim is philosophical speculation. The RG, in contrast, reproduces established relativistic and gravitational relations (Lorentz factor, Schwarzschild radius, perihelion precession, GPS corrections, and many more) to full numerical accuracy using only algebraic geometry. Every result can be verified directly with a calculator, without invoking tensors or metaphysical language. If two works both use the word “framework,” that does not make them equivalent - any more than the word “field” makes Newton and astrology the same discipline. My model stands or falls by calculation, not by vocabulary. I appreciate your caution - skepticism is essential - but precision demands that criticism target the content of the equations, not the titles of other threads. I trust that in our further discussion, you will apply that same skepticism to substance rather than association - with full respect.

@studiot Thanks for engaging I would like to see it if someone already posted something like this. Id be grateful if you could give the link to this post. To clarify: when I write “Spacetime ≡ Energy”, it is not a dimensional equation or a metaphysical claim. It means that what we call spacetime geometry and what we call energy dynamics are two complementary aspects of a single conserved structure. In standard formulations, geometry provides the arena and energy fills it; here, that distinction is removed. Geometry is the bookkeeping of energy transformations, not their container. The framework uses two closure relations: \[ \beta_X^2 + \beta_Y^2 = 1, \qquad \kappa_X^2 + \kappa_Y^2 = 1, \] describing directional (kinematic) and omnidirectional (gravitational) transformations. From these, the usual SR/GR relations emerge algebraically - for example \(E^2 = p^2 + m^2\) and the gravitational time-dilation factor. So “Spacetime ≡ Energy” is shorthand for removing the last unnecessary separation in physics - between structure and dynamics. If anyone is interested, I can post the short derivation of these closure relations directly here. Thanks for the comment. In standard formulations energy is indeed treated as a property within spacetime - derived from the stress-energy tensor or Hamiltonian of a given system. Here, “Spacetime ≡ Energy” does not equate two things, but removes an unnecessary logical separation: if every geometric property (metric, curvature, causal structure) is inferred only through energy distributions, then treating spacetime as an independent background duplicates ontology. In this FRAMEWORK, energy is defined relationally - as the conserved measure of transformation between possible states. Spacetime geometry then becomes the representation of that conservation, not its container. So it’s not that spacetime “is made of energy,” but that both are two sides of the same relational bookkeeping. Yes, precisely - and I’m glad you mentioned Eddington (though my knowledge of his work is quite shallow). His idea that “a coordinate system is strictly unnecessary” is very close to what I’m doing here. In my approach, the physical and mathematical content remain intact - what changes is what we treat as fundamental. Instead of embedding energy inside geometry, I treat geometry itself as the algebraic closure of relational energy transformations. So the equations of SR/GR still hold - they simply emerge as different projections of one conserved relational structure. Fair point and I completely understand the suspicion. A lot of LLM-written physics have made the word framework radioactive lately. But no, this is just me a very human person trying to simplify how we look at SR/GR algebraically. If it reads a bit too polished, that’s probably because I’ve been refining it for months, not minutes. Still, I appreciate the caution we probably need more of it in modern discussions.

This post is for peer testing and discussion. I'm posting this to spark discussion – has anyone seen similar geometric approaches? Students, if you're learning relativity and frustrated with the math, try these derivations and let me know if they click. Test the code, replicate the algebra for other cases (like Mercury's orbit etc), and share your thoughts/results. Could this simplify teaching GR? All equations are purely algebraic and reproduce known results of Special and General Relativity exactly. Feedback on mathematical structure, reproducibility, and numerical testing is welcome. --- Abstract I’m an independent researcher working on a framework called WILL Relational Geometry, which reproduces the main results of SR and GR using only simple algebraic projections on circles and spheres — no tensors, metrics, or differential equations. The model is based on one principle: Spacetime ≡ Energy — meaning geometry and dynamics are not separate but mutually defined. Paper: https://doi.org/10.5281/zenodo.17115270 (October 2025) Full text (PDF): https://github.com/AntonRize/WILL/blob/46ed9a336bd99607033a811cd3160088a07d3851/documents/WILL_PART_I_SR_GR.pdf --- Core Summary - Everything emerges from normalized projections on S¹ and S²: β → kinematic (v/c) κ → potential (√(Rₛ / r)) - Closure rule: κ² = 2β² — a purely geometric relation similar to the virial condition but derived geometrically. - SR and GR factors appear as projections of the same conserved energy relation. - Spacetime and energy transformations are two faces of one invariant. (Full symbolic table attached as image for clarity.) --- Test 1: Photon Sphere Radius GR: Derived via geodesics → r = 1.5 Rₛ. WILL: Set equilibrium θ₁ = θ₂ ⇒ β² + κ² = 1 ⇒ κ² = 2β² ⇒ κ² = 2/3 ⇒ r = Rₛ / κ² = 1.5 Rₛ. For the Sun (M ≈ 1.989×10³⁰ kg, Rₛ ≈ 2.95 km) → r ≈ 4.425 km. Matches GR exactly. --- Test 2: GPS Time Dilation Offset Known value: net +38.5 μs/day (satellite runs faster). WILL: Unified equation for both effects: τ = √(1 – κ²) × √(1 – β²) where κ² = 2GM/(c²r), β = v/c. Python verification (if python not your thing - down below there's link to Desmos projects ready to go): import numpy as np # Constants G = 6.67430e-11 c = 2.99792458e8 # Earth / GPS parameters (SI) M_earth = 5.972e24 # kg R_earth = 6.37e6 # m (mean radius) r_gps = 2.6571e7 # m (GPS orbital radius) # Orbital speed (circular) v_gps = np.sqrt(G * M_earth / r_gps) # Dimensionless parameters beta = v_gps / c kappa_gps = np.sqrt(2 G M_earth / (c**2 * r_gps)) kappa_earth = np.sqrt(2 G M_earth / (c**2 * R_earth)) # Proper-time factors (WILL unified form) tau_gps = np.sqrt(1 - kappa_gps**2) np.sqrt(1 - beta*2) tau_earth = np.sqrt(1 - kappa_earth**2) # Net daily offset (satellite clock faster => positive) offset_us_per_day = (1 - tau_earth / tau_gps) 86400 1e6 print(f"beta = {beta:.9e}") print(f"kappa_gps = {kappa_gps:.9e}, kappa_earth = {kappa_earth:.9e}") print(f"tau_gps = {tau_gps:.12f}, tau_earth = {tau_earth:.12f}") print(f"Offset ≈ {offset_us_per_day:.2f} μs/day") Result: 38.52 μs/day — perfect match. --- Discussion The same framework reproduces: - Lorentz factor and energy–momentum relation. - Schwarzschild potential without curvature formalism. - ISCO (3 Rₛ) and Kerr limits algebraically. - Natural singularity removal without extra assumptions. Interactive demonstrations with ready desmos projects: https://antonrize.github.io/WILL/relativistic-foundations/ https://antonrize.github.io/WILL/ https://antonrize.github.io/WILL/predictions/ https://antonrize.github.io/WILL/results/ --- Invitation This post invites independent testing of a fully algebraic approach to SR and GR that replaces tensor formalism with geometric projections If you reproduce the above results — or find where it fails — please share your numbers. Constructive criticism and falsification proposals are very welcome. --- License: CC BY-NC 4.0 — free for scientific use and replication. © 2025 Anton Rize