Everything posted by Anton Rize
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
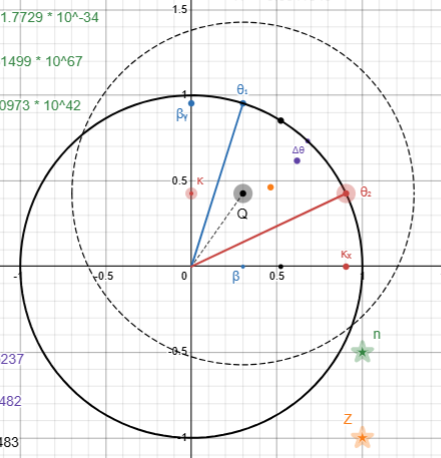
Now I am. It took me a while to decipher your message... And I'm not sure that I understand it correctly. Problem is that I can't see the actual physics behind it. Can you? What I understood in lame terms. Correct me if I'm wrong please: You start by postulating some background structure with the symbols [math]x^\nu[/math], and then introduce another mapping [math]\bar{x}^\mu[/math] Already at this step I have questions: a. On what basis are we justified in postulating any background at all? b. Were all other possible backgrounds proven incompatible before choosing this one? c. Why must a background exist in the first place? d. Does it introduce inconsistencies? e. Is it directly measurable, or purely a descriptive assumption? Then, in order to keep physics “the same” (covariant) within this background, you introduce dummy indices and transformation rules. But again - are these operationally real quantities, or formal devices? Can we measure it? Finally, the “coordinate transformation law for contravariant vectors.” At that point it begins to look like mathematical bookkeeping designed to preserve internal consistency of an unjustified background assumption, rather than expressing physical content. In short, what I see is scaffolding built to stabilise a non-observable, unmeasured, metaphysical claim that the Universe possesses an underlying background structure. There’s no physics in it - only a scaffolding to prevent contradiction within its own premises. --- Earlier you were asking me about [math]\frac{2\pi Q_{\mathrm{orbit}}^{2}}{1-e^{2}},\qquad Q_{\mathrm{orbit}}^{2}:= \beta^2(a)+\kappa^2(a)[/math] and interpretation of the Q parameter. I think I finally got it. And it's so simple: Relational Displacement as Q Parameter Each observer places itself at the relational origin [math](\beta,\kappa)=(0,0)[/math]. When I (as an observer) look at another system, I measure its relational projections [math](\beta,\kappa)[/math] in my own frame. The scalar [math]\boxed{Q^2=\beta^2+\kappa^2}[/math] is the radius at which that other system’s centre appears in my relational plane. If the other system now looks back at me, it again puts itself at [math](0,0)[/math] and applies the same rule. It measures my [math](\beta,\kappa)[/math] and again obtains [math]\boxed{Q^2=\beta^2+\kappa^2}[/math] This expression represents the total deviation of the object from the observer’s relational origin [math](\beta,\kappa)=(0,0)[/math]. Geometrically, the observer is always located at the centre of its own relational circle [math]S^{1}[/math] (or sphere [math]S^{2}[/math]), and any external object appears as a point [math](\beta,\kappa)[/math] on that plane. The scalar [math]Q[/math] therefore measures the radius of relational displacement between two systems. --- Covariance doesn't need to be scaffolded from some arbitrary rules. It's a fundamental property of Relational Geometry.
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
Hahaha! Yeh I agree the "Ouroboros" does sound isosteric. But it also accurately depicts the idea. What can do? I just cant stop my self from being poetic sometimes 🙃. Physics is beautiful and I cant resist it charms ☺️. I understand its unusual and im not asking anyone to believe me. In fact im finding it hard to believe myself. All I did is questioned this assumption about there separation and now im sharing results. Its grate that you brought QM. When this approach applied in QM results are even more unbelievable. I will create a separate topic in QM forum so we can discuss it properly. But for now a little teaser about "infinitely fuzzy": In WILL RG the uncertainty principle isn’t postulated; it arises directly from the closure of energy projection on the unit circle [math]S^1[/math]. When you require that the energy projection returns to its phase after [math]n[/math] full rotations (topological winding number), the minimal definable phase increment is [math]\Delta\theta \ge 2\pi/n[/math]. Two orthogonal projections on [math]S^1[/math], [math]\beta_X = \cos\theta[/math] (momentum-like) and [math]\beta_Y = \sin\theta[/math] (spacetime-like), then satisfy the purely geometric relation [math]\Delta\beta_X \, \Delta\beta_Y \ge \tfrac{1}{2}|\sin 2\theta|\,(\Delta\theta)^2 \;\ge\; \tfrac{1}{2}|\sin 2\theta|\,(2\pi/n)^2.[/math] When mapped to physical quantities through [math]\Delta p \propto \Delta\beta_X[/math] and [math]\Delta x \propto \lambda \propto \Delta\beta_Y[/math], this becomes the familiar Heisenberg bound: [math]\boxed{\Delta x \, \Delta p \gtrsim \hbar.}[/math] So the uncertainty principle appears not as a statistical rule or operator property, but as a geometric consequence of closure on [math]S^1[/math]. Planck’s constant [math]\hbar[/math] then plays the role of a conversion factor between topological winding and dimensional scale - not a “fundamental mystery,” but a calibration invariant. I’ll open a topic in the QM forum to show the derivation step-by-step - it’s quite beautiful, and surprisingly simple once you see it geometrically. A small clarification: my statement [math]\text{SPACETIME} \equiv \text{ENERGY}[/math] isn’t a numerical or dimensional equation like [math]E = S T[/math]. It denotes ontological equivalence - the inseparability of structure and dynamics. In this sense, energy is not something that exists within spacetime, but what constitutes it. I’m using “≡” in the logic/philosophy sense of equivalence (non-separability / mutual definability), not as a numeric equality. In logic, “≡” commonly denotes logical or definitional equivalence (see e.g. ‘Triple bar’ and ‘Logical equivalence’ https://en.wikipedia.org/wiki/Triple_bar), whereas “=” is plain equality. So “SPACETIME ≡ ENERGY” is an ontological equivalence, not a formula like E = S·T. The best way to understand is through category theory - a structural equivalence. Just as two categories can be equivalent (mutually definable but not identical), in RG spacetime and energy are two fully intertranslatable aspects of the same relational structure. So “SPACETIME ≡ ENERGY” means categorical equivalence, not metric equality.
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
It’s also worth noting that the “proportionality constant” between geometry and energy, which GR must import from the Newtonian limit, arises automatically in RG from internal normalization. In GR this constant is written as: [math]\alpha = \frac{8\pi G}{c^2}.[/math] In RG the same quantity follows algebraically from the geometric normalization of energy density: [math]\rho_{\max} = \frac{c^2}{8\pi G r^2},[/math] hence [math]\alpha = \frac{1}{\rho_{\max}\,r^2}.[/math] This shows that the coupling between curvature and energy is not something imposed externally to fit Newtonian gravity - it’s already embedded in the relational structure itself. Philosophically, this means that the very bridge GR must borrow from an older, dualistic theory based on independent background is in RG replaced by an intrinsic self-consistency: the measure of geometry and the measure of energy are the same thing, merely expressed through different projections of a single underlying relation.
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
GR is incredibly complex theory and there's so much remains for me to learn. I don't claim that I have a "proper" understanding of it. In fact Im not even sure that I ever will. Thanks great question! it’s really helpful in focusing the discussion on what the Relational Geometry model is actually doing. Let me clarify my position and outline the core logical chain in a concise way. 1. I’m not questioning background independence in GR itself. (though I'm not fully convinced that it is...) What I’m questioning is the implicit separation between structure and dynamics - between geometry as a pre-existing container and energy as something evolving inside it. In RG, that distinction is removed entirely. Geometry is the relational manifestation of energy. 2. Once this split is removed, the formulation becomes both simpler and fully self-consistent. No differential equations are postulated at the base level (so far works without). Any differential rewriting implicitly commits to a specific parameterisation (and thus extra structure). RG derives relations as coordinate-free algebraic identities; the differential expressions shown are translations into the GR language after a chart is chosen. [math]\kappa^2 = \frac{R_s}{r}.[/math] Here [math]\kappa^2[/math] represents the normalized curvature–energy projection, and [math]R_s = 2Gm_0/c^2[/math] defines the mass scale factor. 4. From this relation, the local energy density follows directly from geometric normalization over the spherical surface due to [math] \kappa [/math] l "lives" on 2-sphere [math] S^2 [/math]: [math]\rho = \frac{\kappa^2 c^2}{8\pi G r^2}.[/math] At the bound condition [math]\kappa^2 = 1[/math] (the horizon limit for non rotation systems [math]r = R_s[/math]) the maximal energy density is reached: [math]\rho_{\max} = \frac{c^2}{8\pi G r^2}.[/math] Hence the relational normalization identity is immediate: [math]\kappa^2 = \frac{\rho}{\rho_{\max}}.[/math] 5. This naturally leads to the expression for geometric pressure, which in this framework arises not as a thermodynamic assumption but from closure constrains as the curvature-tension of the surface itself: [math]P = \frac{c^4}{8\pi G}\frac{1}{r}\frac{d\kappa^2}{dr} = -\,\frac{\kappa^2 c^4}{8\pi G r^2} = -\,\rho c^2.[/math] Thus the equation of state [math]P = -\rho c^2[/math] is not inserted - it’s a necessary condition of curvature balance. The “vacuum pressure” of GR therefore appears as an intrinsic property of energy–geometry itself. 6. Substituting these relations yields a purely algebraic form equivalent to the GR mass function identity: [math]\frac{d}{dr}(r\,\kappa^2) = \frac{8\pi G}{c^2} r^2 \rho(r).[/math] This is not an additional equation - it’s simply the differential translation of the same algebraic closure into GR notation. 7. The same closure produces the scale–curvature relation: [math]\Lambda(r) = \frac{1}{r^2}.[/math] This quantity is not a “cosmological constant” added by hand; it’s the inherent geometric normalization that replaces the need for an external Λ–term. In GR, Λ must be postulated to restore balance between geometry and energy - a consequence of treating them as distinct entities. In RG, the balance is intrinsic, so Λ emerges automatically and scale–dependently. 8. Because the entire construction is scale invariant, the usual distinction between “local” and “global” regimes loses meaning. All scales obey the same algebraic identity [math]\kappa^2 = \rho / \rho_{\max}.[/math] Hence cosmological and microscopic domains are connected by the same relational geometry, not separated by arbitrary boundaries. 9. The singularity problem also dissolves naturally. Since [math]\rho \le \rho_{\max}[/math] by definition, the energy density and curvature can never diverge; [math]\kappa^2 \le 1[/math] sets an intrinsic upper bound. Therefore no infinite curvature or energy density can appear - the geometry self-limits by construction. 10. To summarize the closure loop: [math]\boxed{\kappa^2 = \frac{R_s}{r} = \frac{\rho}{\rho_{\max}}}, \qquad P = -\rho c^2, \qquad \Lambda(r) = \frac{1}{r^2}.[/math] This single algebraic structure captures the full equivalence of geometry and energy without any external parameters, shows scale invariance, eliminates singularities, and matches the empirical curvature–mass–pressure relations observed in both astrophysical and cosmological systems. P. S. All of this remains open for independent verification - that’s precisely why I’m sharing these derivations here.
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
Completely agree. Due to forum format I cant just lay on you guys pages and pages of derivations so Im posting shorted versions and by doing so losing rigor and logical sequence. Maybe if Ill portion it in to digestible peace's?... Lets try and start from the top. This first part is mainly philosophy but we cant move forward without establishing foundations: This document must be read literally. All terms are defined within the relational framework of WILL RG. Any attempt to reinterpret them through conventional notions absolute energies, external backgrounds, hidden containers will produce distortions and misreading. Just like responsibility of formulating lies with the author, the responsibility of interpretation lies with the reader: take the words as written, not as filtered through prior formalisms. Foundational ApproachGuiding Principle [math]\boxed{\textbf{Nothing is assumed. Everything is derived.}}[/math] Epistemic Hygiene — Refusal to Import Unjustified AssumptionsThis framework is constructed under a single epistemic constraint: to derive all of physics by removing one hidden assumption, rather than introducing new postulates. This construction is deliberate and contains zero free parameters. No assumptions are introduced, and no constructs are retained unless they are geometrically or energetically necessary. Principle — Ontological MinimalismAny fundamental theory must proceed from the minimum possible number of ontological assumptions. The burden of proof lies with any assertion that introduces additional complexity or new entities. This is not a statement about the nature of reality, but a rule of logical hygiene for constructing a theory. No Ontological CommitmentsThis model makes no ontological claims about the "existence" of space, particles, or fields. Instead, all phenomena are treated as observer-dependent relational projections. Principle — Relational OriginAll physical quantities must be defined by their relations. Any introduction of absolute properties risks reintroducing metaphysical artefacts and contradicts the foundational insight of relativity. Mathematical Transparency"Mathematics is a language, not a world. Its symbols must never outnumber the physical meanings they encode." 1) Each mathematical object must correspond to an explicitly identifiable relation between observers with transparent ontological origin. 2) Every symbol must be anchored to a unique physical idea. 3) Introducing symbols without explicit necessity constitutes semantic inflation: the proliferation of symbols without corresponding physical meaning. 4) Number of symbols = Number of independent physical ideas. Mathematical Hygiene[math]\boxed{\textbf{Mathematical hygiene is the geometry of reason}}[/math] Ontological Blind Spot in Modern PhysicsThe standard formulation of General Relativity often relies on the concept of an asymptotically flat spacetime, introducing an implicit external reference frame beyond the physical systems under study. While some modern approaches (e.g. shape dynamics) seek greater relationality, we proceed from strict epistemic minimalism — disallowing all background structures, even hidden or asymptotic ones. Historical Pattern: breakthroughs delete, not add - Copernicus eliminated the Earth/cosmos separation. - Newton eliminated the terrestrial/celestial law separation. - Einstein eliminated the space/time separation. - Maxwell eliminated the electricity/magnetism separation. Each step widened the relational circle and reduced the number of unexplained absolutes. The spacetime–energy split is the only survivor of this pruning sequence. The Contemporary Split: An Unpaid Ontological Bill All present-day theories (SR, GR, QFT, ΛCDM, Standard Model) are built with a bi-variable syntax: [math]\underbrace{\text{fixed manifold + metric}}_{\text{structure}} \;+\; \underbrace{\text{fields + constants}}_{\text{dynamics}}[/math] No observation demands this duplication; it is retained only because the resulting Lagrangians are empirically adequate inside the split. The split is not an empirical discovery but an unpaid ontological debt. Empirical Bankruptcy of the Separation - Local energy conservation is verified only after the metric is declared fixed; no experiment varies the volume of flat space and checks calorimetry. - Universality of free fall tests [math]m_i = m_g[/math] numerically, not the claim that inertia resides in the object rather than in a geometric scaling relation. - Gravitational-wave polarisations test spin content, not ontology; extra modes can still be called "matter on spacetime". - Casimir/Lamb shift measure differences of vacuum energy between two geometries; the absolute bulk term is explicitly subtracted, leaving the split intact. In short, every “test” is an internal consistency check of a formalism that already presupposes two substances. None constitute positive evidence for the split. Consequence Until an experiment varies the amount of space while holding everything else fixed, the spacetime–energy separation remains an un-evidenced metaphysical postulate — the last geocentric epicycle in physics. Ontological Minimalism If no empirical or logical ground justifies the distinction between structure and dynamics, the distinction must be dissolved. [math]\textbf{SPACETIME} \equiv \textbf{ENERGY}[/math] This equivalence is not algebraic but ontological: spacetime and energy are two descriptive projections of a single invariant entity we call WILL. Unifying Principle Removing the Hidden AssumptionFalse Separation (Lemma) Any model that treats processes as unfolding within an independent background necessarily assigns to that background structural features (metric, orientation, or frame) not derivable from the relations among the processes themselves. Such a background constitutes an extraneous absolute. Proof Suppose an independent background exists. Then at least one of its structural attributes — metric relations, a preferred orientation, or a class of inertial frames — remains fixed regardless of interprocess data. This attribute is not relationally inferred but posited a priori. It violates relational closure by introducing a non-relational absolute external to the system. Hence the separation is illicit. Corollary (Structure–Dynamics Coincidence) To avoid the artifact of False Separation, the structural arena and the dynamical content must be identified: geometry is energy, and energy is geometry. Working Principle: Removing the Hidden Assumption (Principle) [math]\boxed{\textbf{SPACETIME} \;\equiv\; \textbf{ENERGY}}[/math] This is not introduced as a new ontological entity but as a principle with negative ontological weight: it removes the hidden unjustified separation between “geometry” and “dynamics.” Space and time are not containers but emergent descriptors of relational energy. Remark (Auditability) The Working Principle is foundational but testable: it is subject to (i) geometric audit (internal logical consequences) and (ii) empirical audit (agreement with empirical data). Summary This Principle does not add, it subtracts: it removes the hidden assumption. Structure and dynamics are two aspects of a single entity that we call — WILL. What is Energy in a Relational Framework?Across all domains of physics, one empirical fact persists: in every closed system there exists a quantity that never disappears or arises spontaneously, but only transforms in form. This invariant is observed under many guises — kinetic, potential, thermal, quantum — yet all are interchangeable, pointing to a single underlying structure. Crucially, this quantity is never observed directly, but only through differences between states: a change of velocity, a shift in configuration, a transition of phase. Its value is relational, not absolute: it depends on the chosen frame or comparison, never on an object in isolation. Moreover, this quantity provides continuity of causality. If it changes in one part of the system, a complementary change must occur elsewhere, ensuring the unbroken chain of transitions. Thus it is the bookkeeping of causality itself. Definition (Energy) Energy is the relational measure of difference between possible states, conserved in any closed whole. It is not an intrinsic property of an object, but comparative structure between states (and observers), always manifesting as transformation. Deriving the WILL StructureHaving established the Working Principle by removing the illicit separation of structure and dynamics, we now derive its necessary geometric and physical consequences. This single principle enforces closure, conservation, and isotropy of the relational structure, leading to a unique set of geometric carriers for energy. Definition (WILL) WILL ≡ SPACE–TIME–ENERGY is the unified relational structure determined by the Working Principle. All physically meaningful quantities are relational features of WILL; no external container is permitted. Lemma (Closure) Under the Working Principle, WILL is self-contained: there is no external reservoir into or from which the relational resource can flow. Lemma (Conservation) Within WILL, the total relational transformation resource (energy) is conserved. Lemma (Isotropy from Background-Free Relationality) If no external background is allowed, then no direction can be a priori privileged. Thus the admissible relational geometry of WILL must be maximally symmetric (isotropic and homogeneous) at the level at which it encodes the conserved resource. Classification of Minimal Relational Transformations Given Closure, Conservation, and Isotropy, the minimal carriers are: (a) Directional (Kinematic) Relation: The simplest non-trivial relation is between two distinct states (A and B). The minimal description of this directed relation requires a single degree of freedom (the axis connecting A and B). For self-containment, the 1D geometry must be closed, uniquely specifying the circle. [math]S^{1}[/math] (b) Omnidirectional (Gravitational) Relation: The simplest isotropic relation is between a central state (A) and the locus of all states equidistant from it. The minimal closed, maximally symmetric 2D carrier is the 2-sphere. [math]S^{2}[/math] Theorem (Minimal Relational Carriers of the Conserved Resource) The only closed, maximally symmetric manifolds that can serve as minimal carriers of the conserved relational resource are: (a) [math]S^{1}[/math] for directional (one-degree-of-freedom) relational transformation. (b) [math]S^{2}[/math] for omnidirectional (central, all-directions-equivalent) relational transformation. Proof • For one relational degree of freedom, the classification of connected closed 1-manifolds yields [math]S^{1}[/math] as the unique option (up to diffeomorphism); its isometry group acts transitively with isotropy at each point. • For an omnidirectional relation from a distinguished center, the encoding manifold must be a closed, simply connected, constant positive curvature 2-manifold with full isotropy at every point. By the classification of constant-curvature surfaces, [math]S^{2}[/math] is the maximally symmetric representative. Nontrivial quotients spoil global isotropy and are excluded. Corollary (Uniqueness) Under the Working Principle with Closure, Conservation, and Isotropy, [math]S^{1}[/math] and [math]S^{2}[/math] are necessary relational carriers for, respectively, directional and omnidirectional modes of energy transformation. Remark (Non-spatial Reading) Throughout, [math]S^{1}[/math] and [math]S^{2}[/math] are not spacetime geometries. They are relational manifolds encoding the closure, conservation, and isotropy of the transformational resource. Ordinary spatial and temporal notions are emergent descriptors of patterns within WILL. Summary By removing the hidden assumption (False Separation), we arrive at the Working Principle [math]\text{SPACETIME}\equiv\text{ENERGY}[/math]. From this we deduce: (i) closure, (ii) conservation, (iii) isotropy, and hence (iv) the unique selection of [math]S^{1}[/math] and [math]S^{2}[/math] as minimal relational carriers for directional and omnidirectional transformation. These objects are non-spatial encodings of conservation and symmetry; they are enforced by the principle rather than assumed independently. Let me know if this format is suitable for you guys and ill continue.
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
@KJW Thank you for this very sharp question - it goes straight to the physics. Lets try to figure it out together. 1) Methodological frame (RG vs GR) GR treats geometry as a pre-existing stage and derives the shift from a small difference between the azimuthal and radial frequencies in the Schwarzschild field. RG is ontology-first: there is no background stage. The “geometry” of motion emerges from two conjugate energetic projections that form a closed cycle. In symbols I keep using β (kinetic projection) and κ (potential projection). Their sum Q² = β² + κ² is a dimensionless measure of the cycle’s energetic content at the characteristic orbital scale. Its like total projectional scale. 2) Why the formula really is a perihelion shift In RG the orbit is not integrated in the classical sense - there is no metric-based trajectory. Instead, we follow one full κ–β energy-exchange cycle until the system returns to its initial total energy. At that point, the angular phase of the cycle has advanced slightly beyond 2π. That excess phase, when mapped onto the geometric ellipse defined by (a, e), corresponds exactly to the observed perihelion shift: Δφ = 2π Q² / (1 − e²). 3) Checks and limits • Circular limit: for e → 0 the expression gives Δφ = 2π Q². In the weak-field regime β² ≈ GM/(rc²) and κ² = 2GM/(rc²), hence Q² = 3GM/(rc²). This reproduces the familiar 6π GM/(rc²) circular value. There is no paradox here: a perfect circle has no distinguished perihelion point, so the quantity is a formal phase surplus per cycle. For small e it coincides with the limit from the elliptic family. • Weak field vs not-only: the algebra itself is not tied to a perturbative metric expansion; it is a relational closure. Numerically, in weak fields it agrees with the standard GR value. In stronger fields the same expression remains predictive. Example: star S2 around Sgr A* Using the observational parameters M = 4.30×10⁶ M☉, a ≈ 1000 AU, e ≈ 0.884, we obtain R_s = 1.27×10⁷ km, r_p ≃ 116 AU, r_a ≃ 1884 AU, v_p ≃ 7.9×10³ km/s, and a precession per orbit Δφ ≃ 12.6 arcmin, matching the observed general-relativistic shift without invoking the Schwarzschild metric. In other words, the same measurable angle emerges from the relational closure. A brief aside: the same Q² also correctly flags the photon-sphere separatrix. At r = 1.5 R_s one has κ² = 2/3, β² = 1/3, hence Q² = 1, which marks the null circular configuration - consistent with Q² carrying information about orbit families. It also plays a main role in predicting rotation curves of the 175 galaxys from SPARC database. I got RMSE=20.23 km/s with no DM involved no speculations or free parameters and fixed Y*=0.66 for every galaxy which is quite remarkable I think. You can find the details here: https://antonrize.github.io/WILL/calculator/ But most important is to remember that ontologically GR and RG describing very different Universes. One is "interactions in the box" the other is more of a “there’s-no-spoon” situation if you know what I mean. Your question is exactly the right one to ask here; thanks again for pressing on the physics. P. S. Also lets not forget that my interpretation could be completely wrong. @Markus Hanke Thank you very much for this thoughtful comment - and actually, for your earlier questions as well. It was your request for an explicit orbital trajectory of a test particle that pushed me to go back to the algebra and work out a fully relational version of orbital dynamics. As a result, Part I of the main document now includes a new section called “Relational Orbital Dynamics”. So, in a very direct sense, that development exists thanks to your challenge. I fully agree with your point here: the standard perihelion formula is only as approximate as the Schwarzschild metric itself is to the real solar system. Quantifying that deviation would indeed require a full numerical GR simulation including the solar angular momentum and perturbations from other masses - which, to my knowledge, hasn’t been done in complete generality either. That’s exactly why I find it valuable to approach orbital motion from a strictly relational side: no background metric, just the internal balance of the energy projections themselves. It gives us a complementary way to look at the same physics, while staying anchored to measurable quantities. So, thank you again - your question about the trajectory turned out to be the seed for an entire new section of the framework. P. S. If you interested your expertise in GR would be of grate help to falsify or confirm this relational orbital mechanics. I can't relay on my own judgment from within.
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
> @studiot Ok, thanks for explaining - now I see your point much more clearly. And I genuinely appreciate that you raise these foundational concerns; it shows mathematical care, which is precisely what I value too. What you said about different meanings of numbers makes perfect sense. We can’t just throw objects of completely different categories into the same “bucket” and pretend it’s fine - I actually wish I had been taught this way back in school. You may recall that you mentioned earlier that you’re a mathematician. I’d like to take that seriously and ask for your help in exactly the way I originally came here for - independent verification. The thing is, I’m just a self-educating enthusiast. That’s why I don’t ask anyone to believe my results - in fact, I don’t fully believe them myself until they’re independently checked. That’s why I’m sharing all derivations openly. I’ve done everything I can to uncover potential mistakes, but at this point I can’t find any - and neither could any AI system I’ve tested it with. Those are the only resources I have. At the same time, it’s hard for me to accept the results as correct - they seem too grandiose, and I’m too sceptical for that. So I’m stuck in the middle: can’t find where I’m wrong, and can’t quite accept that I might be right. If you have time and interest, I’d be truly grateful if you could look through one or two of the key relations purely algebraically and tell me whether you can spot any hidden assumptions or inconsistencies in the reasoning itself. That kind of objective audit would mean more to me than any praise or criticism. Thanks for engaging so thoughtfully - it’s rare, and I genuinely appreciate it.
-
20% of Russians are sadists
Where did you get this number from? I agree with your view in general but as person who was involved in the rise of the current conflict back in 2013-2014, and who was born and spend most of my life in Ukraine - I can confidently state that there's no fundamental difference between individual Ukrainian and Russian personality's. One by one people are the same. It more resembles a kind of national responsibility dissolving as we saw in Germany from early 1930's up to 1945. The point is that more likely we as a species are still dumb and violent beasts unfortunately.
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
@studiot Thank you for your last post and your very kind words about my mathematical preparation (though it would be better if you would not make any assumptions just based on account's age). I'm glad we've made progress on the c=1 issue and can now move forward. You are correct that I haven't properly responded to your construction: I must be honest: at first glance, it looked like an intentionally absurd "mathematical salad". Your final equation [math]{\sin ^2}x + {\cos ^2}x = \hbar = - {e^{\pi i}}[/math] ...seemed designed to be nonsensical. However, I'm starting to wonder if I misunderstood you. By deliberately introducing [math]\hbar=1[/math] (witch I didn't brought up) into a discussion about Relativity, were you trying to make a deep point about Quantum Mechanics? If so, that's a fascinating and important topic and I have plenty of results to share and discuss. But it's also a separate one, as it brings QM into a thread focused on GR. Before I can answer your other points, I need to know: was that your intention? Are you asking how RG model can possibly unify with Quantum Mechanics? It seems like your firs help about [math]...[/math] solved my problems. Thank you for offer I appreciate it. No I didn't but it sounds interesting.
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
@studiot Ah, I see! This finally clears up our misunderstanding. Your question is about confusing different types of "1". Let's use an analogy: Imagine we want to create an abstract "Feynman Scale" to measure how funny someone is as a physicist. Now, we know a mathematical identity: [math]\sin^2(x) + \cos^2(x) = 1[/math] This '1' is an abstract, dimensionless number. It's the result of a calculation. Separately, we create our convention (our "language"): We set the benchmark for maximum funniness as "1 Full Feynman" (or [math]R_F = 1[/math]). This '1' is the axiom of our system. It's a definition, not a result. Here is the question that shows the category error: Can we say that [math]\sin^2(x) + \cos^2(x)[/math] is equal to "1 Full Feynman"?" Of course not! 😄 One is an abstract mathematical identity. The other is a foundational definition of a system. You are doing the exact same thing by confusing the mathematical identity [math]-e^{\pi i} = 1[/math] (an abstract result) with the physical unit convention [math]c=1[/math] (the foundational axiom of the Natural Units language). That's why I couldn't follow your logic - you are brilliantly mixing two completely different categories! So no, replacing '1' in my equations with [math]c[/math] is not the same as replacing it with [math]\sin^2(x) + \cos^2(x)[/math]. One is a change of language (SI vs. Natural Units), the other is just... mathematical salad. 😉 And Im aware that "1 Full Feynman" is a unit so my analogy is not ideal. But I hope this will clear out this misunderstanding between us so we can concentrate on the substance of the equations instead of notation.
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
💥💥💥💯🦀💃 It's meant to be fireworks and we celebrating hahahaha!!! WE GOT A WINER!!!!! seriously @KJW , thank you so much mate because I was already losing hope completely. Mathematical validation and testing was the soul purpose of this whole post and you are the first and only one who actually did it. thank you so much! Thank you. This is the correct analysis. You've correctly shown my algebraic formula [math]\Delta_{WILL} = \frac{2\pi Q_{merc}^2}{1-e_{merc}^2}[/math] agrees with the known GR result. To answer your excellent question: My formula is composed of two parts: The Numerator ([math]2\pi Q_{merc}^2[/math]): This is the new physics from WILL. The term [math]Q^2 = \kappa^2 + \beta^2[/math] is the instantaneous relational energy budget derived from my framework. The [math]2\pi[/math] converts it to one full orbit. The Denominator ([math]1-e_{merc}^2[/math]): This is standard geometry, not new physics. It's the classical orbital mechanics factor needed to average the instantaneous shift (at radius a) over the full eccentric ellipse, relating the semi-major axis (a) to the semi-latus rectum [math]p = a(1-e^2)[/math]. In short, I am applying the new WILL relational physics (the numerator) to the known, standard geometry of an ellipse (the denominator) to get the final correct result. But I prefer to think about it this way: a circular orbit (e=0) gives a baseline precession of [math]2\pi Q^2[/math]. An elliptical orbit (e>0) simply introduces a standard geometric "deviation from circularity" factor, which is [math]\frac{1}{1-e^2}[/math]. Thank you for spotting it out mate. @studiot I honestly tried to understand what are you saying but - no clue. I just cant see any physics behind this numbers and symbols manipulation. If it make you feel better: "I promise not to use c=1 in my derivation's"🙂
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
And also I don't think we should separate philosophy from physics ever. Allow me the attempt to prove it: Derivation of statement: "Complex mathematics is the consequence of bad philosophy" Classical Keplerian Energy as a WILL-Minkowski ProjectionFor a test body of mass m on a circular orbit of radius a about a central mass [math]M_\oplus[/math], classical Newtonian mechanics gives: [math]\Delta U = -\frac{GM_\oplus m}{a} + \frac{GM_\oplus m}{R_\oplus}[/math] [math]K = \frac{1}{2} m\frac{GM_\oplus}{a}[/math] Adding these and dividing by the rest-energy [math]E_0 = m c^2[/math] yields the dimensionless total: [math]\frac{E_{\text{tot}}}{E_0} = \frac{GM_\oplus}{R_\oplus c^2} - \frac{1}{2}\frac{GM_\oplus}{a c^2}[/math] Projection Parameters and Minkowski-like FormDefine the WILL projection parameters for the surface and the orbit: [math]\kappa_\oplus^2 \equiv \frac{2GM_\oplus}{R_\oplus c^2}[/math] [math]\beta_{\text{orbit}}^2 \equiv \frac{GM_\oplus}{a c^2}[/math] Substituting into the classical equation gives the exact identity: [math]\frac{E_{\text{tot}}}{E_0} = \frac{1}{2}\bigl(\kappa_\oplus^2 - \beta_{\text{orbit}}^2\bigr)[/math] This is already in the form of a hyperbolic difference of squares. If we set [math]x \equiv \kappa_\oplus[/math] and [math]y \equiv \beta_{\text{orbit}}[/math], then: [math]\frac{E_{\text{tot}}}{E_0} = \frac{1}{2}\,(x^2 - y^2)[/math] This is structurally identical to a Minkowski interval in [math](1+1)[/math] dimensions. Physical InterpretationIn classical derivations, this is just the sum [math]\Delta U + K[/math] with a particular choice of potential zero. In WILL Relational Geometry, this form emerges directly from the Energy-Symmetry Law: [math]\Delta E_{A\to B} = \frac{1}{2}\bigl((\kappa_A^2 - \kappa_B^2) + \beta_B^2\bigr)[/math] (with [math](A,B) = (\text{surface},\ \text{orbit})[/math]) This shows that the Keplerian total energy is not an isolated Newtonian artifact but a special case of a deeper geometric structure. The emergence of this Minkowski-like structure from purely energetic principles is a powerful indicator of the deep identity between the geometry of spacetime and the geometry of energy transformation. Lagrangian and Hamiltonian as Ontologically Corrupted ApproximationsThe familiar Lagrangian and Hamiltonian formalisms are not fundamental principles but approximations that arise from collapsing the two-point relational structure of the Energy-Symmetry Law into a single-point description. The "Ontological Collapse"If one commits the ontological violation by identifying the two distinct points, [math]r_A = r_B = r[/math], the relational structure degenerates into a local, single-point function: [math]L(r,\dot r,\dot\phi)=\tfrac{1}{2} m(\dot r^2+r^2\dot\phi^2)+\frac{GMm}{r}[/math] This is precisely the standard Newtonian Lagrangian. Defining the Hamiltonian via the Legendre transformation [math]H = p_r \dot r + p_\phi \dot\phi - L[/math] evaluates to the total energy of the collapsed system: [math]H = T+U = \tfrac{1}{2} m\left(\dot r^2 + r^2 \dot\phi^2\right) - \frac{GMm}{r}[/math] InterpretationIn terms of the collapsed WILL projections [math]\beta^2 = v^2/c^2[/math] and [math]\kappa^2 = 2GM/(rc^2)[/math], the match becomes explicit: [math]L = \tfrac{1}{2} m v^2 + \frac{GMm}{r} \;\;\;\longleftrightarrow\;\;\; \tfrac{1}{2} m c^2\bigl(\beta^2 + \kappa^2\bigr)[/math] [math]H = \tfrac{1}{2} m v^2 - \frac{GMm}{r} \;\;\;\longleftrightarrow\;\;\; \tfrac{1}{2} m c^2\bigl(\beta^2 - \kappa^2\bigr)[/math] Here the + or - signs do not come from [math]\kappa^2[/math] itself (which is always positive), but from the ontological collapse of the two-point relational energy law into a single-point formalism. > Key Message: The Lagrangian and Hamiltonian are not fundamental principles. They are degenerate shadows of a deeper relational Energy-Symmetry Law. Classical mechanics, Special Relativity, and General Relativity all operate within this corrupted approximation. WILL restores the underlying two-point relational clarity. Third Ontological Collapse: Derivation of Newton's Third LawNewton's Third Law is another "degenerate shadow" that arises as a necessary mathematical consequence of this same ontological collapse. Theorem: Newton's Third Law as a Degenerate Consequence The Energy-Symmetry Law ([math]\Delta E_{A \to B} + \Delta E_{B \to A} = 0[/math]) mathematically necessitates Newton's Third Law ([math]\vec{F}_{AB} = - \vec{F}_{BA}[/math]) in the classical limit where the two-point relational energy budget is collapsed into a single-point potential function [math]U(\vec{r})[/math]. Proof: Begin with the foundational Energy-Symmetry Law: [math]\Delta E_{A \to B} + \Delta E_{B \to A} = 0[/math] In the classical limit, this is "corrupted" into a single-point potential function U that depends only on the relative positions: [math]U = U(\vec{r}) \quad \text{where} \quad \vec{r} = \vec{r}_B - \vec{r}_A[/math] The force [math]\vec{F}[/math] is defined as the negative gradient of this potential. (1) Force on B by A: [math]\vec{F}_{AB} = - \nabla_B U(\vec{r}_B - \vec{r}_A) = - \left( \frac{d U}{d \vec{r}} \right) \cdot \left( \frac{\partial \vec{r}}{\partial \vec{r}_B} \right) = - \nabla U(\vec{r})[/math] (2) Force on A by B: [math]\vec{F}_{BA} = - \nabla_A U(\vec{r}_B - \vec{r}_A) = - \left( \frac{d U}{d \vec{r}} \right) \cdot \left( \frac{\partial \vec{r}}{\partial \vec{r}_A} \right) = + \nabla U(\vec{r})[/math] (3) Conclusion: By direct comparison: [math]\vec{F}_{AB} = - \nabla U(\vec{r}) \quad \text{and} \quad \vec{F}_{BA} = + \nabla U(\vec{r})[/math] Therefore, it is a mathematical tautology of the collapsed formalism that: [math]\boxed{ \vec{F}_{AB} = - \vec{F}_{BA} }[/math] This completes the proof. The law of "equal and opposite forces" is revealed to be a degenerate approximation of the more fundamental, generative law of Relational Geometry. General ConsequenceBad philosophy (the ontological separation of Structure and Dynamics) has measurable effects: 1. Inflated Formalism: Equations multiply to compensate for the error. 2. Loss of Transparency: Physical meaning is hidden behind coordinate dependencies. By contrast, good philosophy (**epistemic hygiene**) enforces relational closure and yields simplicity through necessity. > Daring Remark: The historical escalation of mathematical complexity in physics did not reveal deeper reality—it compensated for a philosophical mistake. Once the ontological symmetry is restored, Nature’s laws reduce to algebraic self-consistency. > > [math]\boxed{\text{Bad Philosophy}} \Rightarrow \boxed{\text{Ontological Duplication}} \Rightarrow \boxed{\text{Mathematical Inflation}}[/math] > [math]\boxed{\text{Complex mathematics is the consequence of bad philosophy.}}[/math] Yes I know its to daring and to radical. But this is exactly why I love it so much. It makes you think it makes you feel and maybe it will help someone to see the bigger picture...
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
Its funny that among physicists I'm seen as philosopher and among philosophers I'm seen as physicist. Im like a nomad 😩. I don't know where exactly the line between physics and philosophy lies but im quiet sure that if "philosophy" makes unique numerical testable predictions + recovering standard results it becomes ""physics" is it not?
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
@Markus Hanke Your last statement is an assertion, not a criticism. For it to become a criticism, it has to obtain an objective form like an equation or a well defined logical construct. But let's explore your assertion: 1. Let's assume you are correct, and I am "tacitly using" concepts that require a metric. 2. However, as you've seen, I can't find this "hidden metric" in my algebra. You can't find it. It doesn't appear in the equations. 3. And most importantly, it is not needed to derive the correct precession of Mercury to [math]10^{-7}[/math] precision, as shown by my algebraic formula: [math]\Delta\phi = (2\pi Q^2)/(1-e^2)[/math]. So, if this "hidden metric" is mathematically invisible, algebraically unnecessary, and operationally redundant... what is its physical meaning? It becomes a useless entity. Sorry, but this is why your assertion not only is not a valid criticism, but also just not valid at all.
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
Welcome @Xerxes This is a geat observation. Im not familuuer with Category Theory as much as I should yet... But I can see the resemblance. Thank you for pointing it out. Yes but I cant follow your logic from this c=1 to this c = -(eπi). This is a misunderstanding. Everything derived from essentially just methodology. Have a look in the beginning of this document https://github.com/AntonRize/WILL/raw/main/documents/WILL_PART_I_SR_GR.pdf from where im starting and how derivation progress. If you don't want to look at .pdf let me know and ill post this part here but its a bit lengthy. Thank you for joining us @swansont Yes but why do we have to limit ourselves? Why not both the "HOW?" and the "WHY?"? This is exactly what im trying to do. Yes! 100% agree.
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
Showing complete misunderstanding. Proven Wrong. Proven Wrong. Due to my results allying with empirical data, your different results would be just plain wrong. So again proven wrong. @Markus Hanke stop building argument on personal (often wrong) opinion and show which definition is faulty not which word sounds like GR. Sorry I have no idea what you mean by this. Cant see any connections at all. There must be some misunderstanding between us. I moved to AU some time ago in my 30's. English is my third languedge. I can talk I can read but I cant spell at all 🙃. Also for topics like this I prefer to think and wright in my native language due to my English vocabulary isn't big enough sometimes.
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
@joigus Thank you for this response. I'm glad that we finally resolve this misunderstanding about the [math]S^1[/math]/hyperbolic geometry. That clears the air, and now we can discuss the real substance of the model. You've raised three crucial objections: that the model is (1) a tautology ("circular logic"), (2) philosophically misguided ("physics is about metrics"), and (3) non-covariant (because it doesn't use tensors). Let's address them in order. 1. On Tautology ("Circular Logic")You argue that the definitions are "circular" and that there is "no mystery there". If I only said [math]\beta = \cos \theta_1[/math] and stopped, you would be 100% correct. But that is not what I do. The model is generative, not descriptive. I don't assume [math]\beta[/math]; I derive the framework that produces it. The full derivation is in the paper (https://github.com/AntonRize/WILL/raw/main/documents/WILL_PART_I_SR_GR.pdf), but the short logical chain is this: This chain generates new, testable physics (like the precession formula [math]\Delta\phi = \frac{2\pi Q^2}{1-e^2}[/math]) from first principles. This is the opposite of a tautology; it's a predictive, generative structure. 2. On Philosophy ("Physics is about metrics")You said: "But physics is about metrics, distances and angles. It just is." Here, we have a fundamental disagreement. From my perspective, metrics, distances, and angles are the bookkeeping (the 'how'), not the physics (the 'why'). They are the anthropocentric representation, the "grammar of measurement" we use to describe relations. The physics lies in the fundamental symmetries and invariants that dictate the rules of this bookkeeping. My model seeks to define those rules algebraically, before any coordinate system or metric is postulated. 3. On Covariance (Algebra vs. Tensors)This is your most important point. You perfectly defined covariance: "...all observers agree on what they measure when everything is expressed in terms of invariants". You then equated this principle with tensors. But tensors are just one implementation of covariance (a differential one). WILL implements covariance algebraically. In GR, the invariant is [math]ds^2[/math]. In WILL, a key invariant is the Energy-Symmetry Law, which states that for any two observers/states (A and B), the energy transfer is perfectly balanced: [math]\Delta E_{A \to B} + \Delta E_{B \to A} = 0[/math] I derive this by defining the specific energy for a transition as the sum of the changes in the potential and kinetic budgets: [math]\Delta E_{A \to B} = \Delta U + \Delta K = \frac{1}{2}(\kappa_A^2 - \kappa_B^2) + \frac{1}{2}(\beta_B^2 - \beta_A^2)[/math] [math]\Delta E_{B \to A} = \frac{1}{2}(\kappa_B^2 - \kappa_A^2) + \frac{1}{2}(\beta_A^2 - \beta_B^2)[/math] Summing them algebraically gives zero. This identity is WILL's form of covariance. It holds for all observers, yet requires no tensors. This single algebraic law has profound, non-trivial consequences: A) The Geometric Origin of the Universal Speed Limit ([math]v \le c[/math]) The speed limit is a foundational property of the [math]S^1[/math] relational manifold itself. The kinematic framework is defined by the conservation of two projections: the "Amplitude Component" ([math]\beta[/math], velocity) and the "Phase Component" ([math]\beta_Y[/math], internal structure). These are bound by the geometry's Pythagorean identity: [math] \beta^2 + \beta_Y^2 = 1 [/math] A state [math]\beta > 1[/math] (i.e., [math]v > c[/math]) would algebraically force: [math] \beta_Y^2 = 1 - \beta^2 < 0 [/math] This would mean the "Phase Component" [math]\beta_Y[/math] becomes an imaginary number. Therefore, a state [math]v > c[/math] is not just forbidden; it is geometrically undefined in this framework, as it would represent a state with no real internal structure. B) The Nature of Light (No Rest Frame) For massive particles ([math]\beta < 1[/math]), the energy exchange is symmetric, split between two orthogonal branches (X and Y), giving the [math]\frac{1}{2}[/math] factor. But for light, [math]\beta=1[/math]. This means its complementary projection [math]\beta_Y = \sqrt{1-\beta^2} = 0[/math]. The symmetric split between two orthogonal branches (X and Y) disappears. The exchange can't be partitioned; it collapses onto a single axis. This is why light experiences twice the gravitational effect (e.g., lensing [math]\Phi_\gamma = \kappa^2 c^2[/math] vs. mass [math]\Phi_{mass} = \frac{1}{2}\kappa^2 c^2[/math]). Light is the boundary state where this energy symmetry breaks. This isn't just philosophy; it's testable. In Appendix I, I validated this law on the real-world Earth-GPS system: [math]\Delta E_{Earth \to GPS} = 6.1265399845 \times 10^{-10}[/math] [math]\Delta E_{GPS \to Earth} = -6.1265399845 \times 10^{-10}[/math] Sum = 0. This confirms the law holds to machine precision. It is a true invariant.
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
Thankyou. I will assume that you rad my privies 2 reply's and for some reason find them incomplete. @studiot To be perfectly clear: Yes, absolutely. The symbols E, p, m in the equation E^2 = p^2 + m^2 have different dimensions than the E, p, m in the equation E^2 = (pc)^2 + (mc^2)^2. This is not an error; it is the entire point. The blog post you quoted is correct that c=1 is a formal change of unit system, but it is philosophically incorrect to call it "WRONG". Here is my position: 1. Physics must be Universal: A fundamental physical law must be valid for any civilization, regardless of their species-specific, historical units (like "meters" or "Zglorp-tails"). 2. c=1 is Fundamental: This formulation, where c is a dimensionless unity, is the fundamental expression of physical reality. It is the only "intergalactic standard." 3. SI Units are for Bookkeeping: The SI-unit equation E^2 = (pc)^2 + (mc^2)^2 is a secondary translation of that fundamental law. We "restore c" only for the practical task of comparing our universal formulas to human-centric SI measurements. My framework does not "lose the physics". It removes the anthropocentric "linguistic layer" to reveal the physics. This is why WILL is built from the ground up on universal, dimensionless projections like [math]\beta=v/c[/math] and [math]\kappa = v_e/c[/math]. These ratios are the same for everyone in the Cosmos.
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
The full derivation is here (right click save as to download .pdf) https://github.com/AntonRize/WILL/raw/main/documents/WILL_PART_I_SR_GR.pdf In short its just as I said math fits in to places naturally. I didn't even knew the GR solution when I derived this. Its just make sense and every operation has clear physical meaning like it was "meant" to be this way isn't it? From removing the separation between structure and dynamics I derived the core principle SPACETIME ≡ ENERGY. From it constrains I derived relational manifolds (not spacetime geometry but energy relation careers) circle S^1 for 1 degree of freedom with projections beta=v/c, beta_Y=√(1-beta^2) 2 sphere S^2 for 2 degrees of freedom with projections kappa=v_e/c=√(R_s/r), kappa_X=√(1-kappa^2) Due to them being different projections of the same conserved quantity the "exchange" rate is 2DOF/1DOF=κ²/β² = 2 for energy closed systems (per period for elliptical orbits) Total projection as a vector on (kappa, beta) plane Q=√(kappa^2+beta^2) end then 𝐃𝐢𝐦𝐞𝐧𝐬𝐢𝐨𝐧𝐥𝐞𝐬𝐬 𝐩𝐫𝐨𝐣𝐞𝐜𝐭𝐢𝐨𝐧 𝐩𝐚𝐫𝐚𝐦𝐞𝐭𝐞𝐫𝐬 𝐟𝐨𝐫 𝐌𝐞𝐫𝐜𝐮𝐫𝐲: κₘₑᵣ꜀ = √(Rₛₛᵤₙ / aₘₑᵣ꜀) βₘₑᵣ꜀ = √(Rₛₛᵤₙ / 2aₘₑᵣ꜀) 𝐂𝐨𝐦𝐛𝐢𝐧𝐞𝐝 𝐞𝐧𝐞𝐫𝐠𝐲 𝐩𝐫𝐨𝐣𝐞𝐜𝐭𝐢𝐨𝐧 𝐩𝐚𝐫𝐚𝐦𝐞𝐭𝐞𝐫: Qₘₑᵣ꜀ = √(κₘₑᵣ꜀² + βₘₑᵣ꜀²) 𝐂𝐨𝐫𝐫𝐞𝐜𝐭𝐢𝐨𝐧 𝐟𝐚𝐜𝐭𝐨𝐫 𝐟𝐨𝐫 𝐭𝐡𝐞 𝐞𝐥𝐥𝐢𝐩𝐭𝐢𝐜 𝐨𝐫𝐛𝐢𝐭 𝐝𝐢𝐯𝐢𝐝𝐞𝐝 𝐛𝐲 𝐨𝐧𝐞 𝐨𝐫𝐛𝐢𝐭𝐚𝐥 𝐩𝐞𝐫𝐢𝐨𝐝: (1 − eₘₑᵣ꜀²) / 2π 𝐅𝐢𝐧𝐚𝐥 𝐖𝐈𝐋𝐋 RG 𝐩𝐫𝐞𝐜𝐞𝐬𝐬𝐢𝐨𝐧 𝐫𝐞𝐬𝐮𝐥𝐭: Δφ₍WILL₎ = (Qₘₑᵣ꜀²) / [(1 − eₘₑᵣ꜀²) / 2π] = (2πQₘₑᵣ꜀²) / (1 − eₘₑᵣ꜀²) @KJW Please tell how to use Latex here this reformatting in to Unicode every time will drive me crazy soon 🙃.
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
Do you understand that distance can be relational without metric involved? Also try google sometimes: "Areal radius is a term primarily used in cosmology and general relativity to describe a specific radial coordinate that measures the "area" of a spherical surface centered on an observer within a curved spacetime. It is defined so that the surface area of such a sphere is A=4πR2, where R is the areal radius." I understand that its different from what you used to, but if everything would be the same as GR it wouldn't be a new idea isn't it? Its not that hard. You can define distance between n number of objects without a "grid" just relational. I already showed you set of equations and 2 demos projects with numerical conformations. I don't know what else I can do... Means that relational properties comes first and they determent geometry. Are you aware that you haven't wrote a single equation here? We can exchange opinions with you forever. In the end its numbers that meters.
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
@Markus Hanke I made 2 desmos projects for you: https://www.desmos.com/geometry/nrtnjramrl - calculates aphelion of Mercury using the set of algebraic equations I listed above r_{a}=\frac{-R_{s}-\sqrt{R_{s}^{2}-8E_{d}\left(-h^{2}\right)}}{4E_{d}}=6.9762118617\times10^{10} m. empirical value r_a = 6.982×10^10 m (discrepancy due to estimated input values, but you got the point) https://www.desmos.com/geometry/hkxjqfkchp - calculates perihelion precession of Mercury \Delta_{WILL}=\frac{2\pi Q_{Merc}^{2}}{\left(1-e_{Merc}^{2}\right)}\ = 5.0208724126\times10^{-7} radians/orbit. empirical value \Delta_{Merc}=5.02 \times10^{-7} radians/orbit.
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
@Markus Hanke I'm very disappointed. I genuinely was hoping to finally have a meaningful conversation... I took your question seriously and spend time to provide you with an answer. You on the other hand didn't even try to understand which I can see clearly by your comment "Some of these things are also observer-dependent" - its a relational framework most of "these things" are observer-dependent. You state that concepts like "gradient," "orthogonality," and "conserved quantity" cannot "meanfully exist" without a spacetime manifold and a metric (gμν). My position is that these concepts emerge algebraically from the relational geometry (S¹ × S²), before any metric is postulated. You seem to be mistaking my algebraic definitions (the physics) for their metric descriptions (the coordinate overlay). To move this from opinion to mathematics, please identify which of my exact algebraic definitions you claim is (or illicitly requires) a metric tensor. Objection 1: "You use 'r', 'gradients', 'orthogonality', and 'areas' which require a metric." Response: I define these algebraically. Which of the following definitions is a metric tensor? A) r ≡ Rₛ / κ² (My definition of the areal radius 'r' as an algebraic output of a field measurement κ, not an a priori coordinate.) B) ∇κ (The physical gradient of the scalar potential field κ. I define "radial" as this direction.) C) The intrinsic orthogonality on the S² manifold. (I define "tangential" as the direction orthogonal to ∇κ on my base manifold S², which is the source of geometry, not its product.) Objection 2: "You use 'conserved quantities' which require Killing vectors (metric symmetries)." Response: My invariants are algebraic, not differential. Which of these algebraic budgets do you claim requires a Killing vector? A) ΔE = 0.5 * (β² - κ²) (My fundamental trajectory invariant, derived from the Energy-Symmetry Law, not a ∂ₜ symmetry of a metric.) B) h = r₀ * βₜ,₀ (The definition of angular momentum, which I noted is conserved only because spherical symmetry was a given input - i.e., ∇κ is purely radial.) Objection 3: "You use a 'nebulous scalar' and cannot encode an EM field or non-uniform source." Response: I explicitly defined the general case in my "Case B." Which of these formalisms is an invalid source model? A) κ²(r) = Rₛ / r (The single scalar only for the spherically symmetric case.) B) κ(r, Ω) (The scalar field on S² I use to encode any non-uniform source, such as your EM field, as a directional map. This is not a single scalar.) Objection 4: "You don't account for non-linearity." Response: My model is algebraically non-linear at its foundation. Which of these core equations do you claim is linear? A) ΔE = 0.5 * (β² - Rₛ/r) (The invariant energy budget itself is a non-linear relation between β and r.) B) (2ΔE) · rₚ² + Rₛ · rₚ - h² = 0 (The final algebraic equation I derived to solve the trajectory.) You are assuming these concepts imply a metric. I am deriving them from an algebraic foundation that precedes it. The burden is now on you to show which definition is faulty, not which word sounds like GR. P. S. And regarding your comment about LLM-AI: I'm using AI to translate in to English and reformat Latex in to Unicode. If I would allow AI to wright answers for me this would be a very short thread. Do you think there's an AI who can handle tasks like this? Im using Gemini and it cant. If you know one that can please give me a link Id love to talk to it.
-
A Methodological Challenge: Purging Physics of "Semantic Inflation"
@pinball1970 And you call it "pull it apart"? I cant even understand your argument. Can you express yourself a bit clearer? @swansont Two clarifications: (i) I don’t claim β is Lorentz-invariant; it’s an operational, dimensionless primitive within a chosen frame. What I call “invariant” is the form of the closure identity (e.g. β^2+βY^2=1), not each component separately. (ii) x,t become “measurable” only after conventions (synchronization, frame, units). They are representational choices, not primitives. MH targets exactly this: primitives first (operational, dimensionless), coordinates later as derived bookkeeping. Pedagogy is a separate (and open) question; ontology shouldn’t be outsourced to convenience.
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
Thanks for jumping in @Markus Hanke Great question! Your premise is a bit flowed. Within WILL RG we not dealing with non physical imaginary regions. Region is not a physical object - you cant measure it. You'll have to postulate one and we don't want to postulate non physical made up stuff. Instead we can work with relations within given system. Hit-or-miss in WILL (short, coordinate-free) • We do not use metrics or geodesics. Dynamics = a single invariant budget: ΔE = 0.5*(β² − κ²). • “Radial” is defined without coordinates: it is the direction of ∇κ (meridian on S²). “Tangential” is orthogonal to it on the relational sphere. • Case A (stationary spherical source): the field is one scalar, κ²(r) = Rₛ / r, equivalently r = Rₛ / κ². Given initial state at r₀ with total speed β₀ (where β₀² = βᵣ,₀² + βₜ,₀²) and tangential part βₜ,₀, two constants follow: ΔE = 0.5*(β₀² − κ₀²), and h = r₀ * βₜ,₀ (specific angular momentum; conserved by spherical symmetry). • Periapsis is where βᵣ = 0, hence βₚ = βₜ,ₚ = h / rₚ and κₚ² = Rₛ / rₚ. Invariance gives a single algebraic equation for rₚ: 0.5*(h² / rₚ² − Rₛ / rₚ) = ΔE, i.e. (2ΔE)·rₚ² + Rₛ·rₚ − h² = 0, solve for rₚ > 0. Hit if rₚ ≤ R_body. • Case B (non-uniform/radiation field): replace the scalar by a directional map κ(r, Ω). ΔE remains invariant; “radial” stays ∇κ. There is no global conservation of h without symmetry, so propagate the tangential budget step-by-step relative to ∇κ. The same hit test applies once rₚ is obtained. Takeaway: WILL computes trajectories by conserving algebraic budgets (ΔE, and h only when symmetry allows). A metric can be added later as a descriptive overlay, not as the engine. PARAMETER GLOSSARY • c - speed of light (units: length/time). • G - gravitational constant. • M - central mass (Case A). • R_s - Schwarzschild radius, R_s = 2 G M / c^2 (units: length). • r - areal radius (units: length), defined by the observable area A via A = 4π r^2. In stationary spherical exterior: r = R_s / κ^2. • r_0 - initial areal radius (units: length). • r_p - periapsis (closest-approach) radius (units: length). • R_body - physical radius of the extended body (units: length). • β - total kinematic projection (dimensionless), β = v / c, with 0 ≤ β ≤ 1. • β_r - radial component of β, defined relative to the local “radial” direction. • β_t - tangential magnitude of β, β_t = √(β^2 − β_r^2). • β_0 - initial β; β_t0 - initial tangential component of β. • β_p - total β at periapsis; at periapsis β_r = 0, so β_p = β_t,p. • κ - potential projection (dimensionless). - General (non-uniform) field: κ = κ(r, Ω), a directional map on S². - Stationary spherical exterior: κ^2(r) = R_s / r (so 0 < κ^2 < 1 for r > R_s). • κ_p - κ at periapsis; in spherical exterior: κ_p^2 = R_s / r_p. • Ω - direction on the unit sphere S² (solid angle label for anisotropic fields). • ∇κ - spatial gradient of κ; defines the “radial” direction locally (coordinate-free). • h - specific angular momentum (units: length), h = r · β_t. - Conserved only when spherical symmetry holds (Case A). - Not a global invariant in generic non-uniform fields. • ΔE - relational energy budget (dimensionless), invariant along the trajectory: ΔE = 0.5 · (β^2 − κ^2). (In spherical exterior this yields the periapsis equation 0.5 · (h^2 / r_p^2 − R_s / r_p) = ΔE.) Notes on domains and use: • Exterior of a compact spherical source: r > R_s ⇒ 0 < κ^2 < 1 and 0 ≤ β ≤ 1. • “Radial” and “tangential” are defined operationally: radial ≡ direction of ∇κ; tangential ≡ any direction orthogonal to ∇κ on S². • Conserved quantities: ΔE always; h only when symmetry (spherical) supplies a corresponding Killing vector. @joigus I think there may still be a misunderstanding here. In a Minkowski diagram the axes X and Y are physical coordinates (ct, x) defined within a metric. In the S¹–S² formulation of WILL, X and Y are dimensionless relational projections – amplitude- and phase-like components of a single conserved quantity. They are not spacetime coordinates; no metric is postulated at that stage. Could you please specify which part of this distinction remains unclear?
-
Simplifying SR and GR with Relational Geometry — Algebraic Derivations Without Tensors. Testing and discussion.
Thank you for jumping in @KJW I understand it might feel unconventional at first. Try this page https://antonrize.github.io/WILL/relativistic-foundations/ I wrote it specifically to ease understanding. There's a lot of visual and interactive elements, definitely better than scrolling through long forum debates. No. I'm doing exactly opposite: removing assumptions and anthropocentric elements. If you will follow the link you will see it immediately. Good point! I like your grounded approach. But lets have a look what exactly we measuring: When we “measure distance,” what we actually record is not some absolute spatial entity but a relational configuration of events - a count of oscillations, light pulses, or clock ticks exchanged between systems. Likewise, when we “measure time,” we don’t access a primitive flow; we compare periodic processes and define one as our reference. Both quantities - distance and time - are abstractions distilled from relational data. So in WILL, the goal is not to deny measurements, but to clarify that what is measured are relations, while what is inferred (like space or time) is representational. The relational structure comes first; coordinates appear only after we project that structure into human-friendly form. So yes coordinate space and time not primitive ingredients but the result of our conventional choice of representation. And that what you can call: Universe doesn't know and doesn't care about any coordinate system of ours. Completely agree with you on this. And this is precisely what im trying to show here. --- The remarkable thing is when you adopt this relational view the math is just fits in to places naturally! Its simpler cleaner requires no unphysical constructions (like coordinate system) and perfectly allying with experimental results. And I cant believe it myself! That's why I posted it here.