Anton Rize

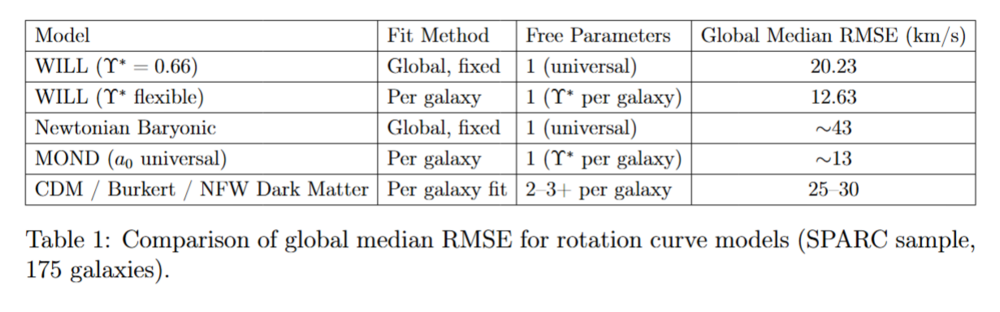
@swansont Thank you for the structured critique. You raise specific, testable objections regarding the statistical standard and the physical shape of the rotation curves. I have completed the full statistical analysis to address your concerns about the metric and the fit quality. You rightly pointed out that RMSE can mask shape mismatches, so I ran the test using Reduced Chi-Squared ([math]\chi_\nu^2[/math]). The results reveal exactly what is happening physically. I compared my strict Zero-Parameter geometric model against a minimal One-Parameter variation (standard astrophysical practice). --- COMPARISON OF PREDICTIVE POWER (SPARC, 175 Galaxies) --- 1. FIXED QWILL (0 Free Parameters): Constraint: Fixed Global [math]\Upsilon_* = 0.66[/math] Law: [math]V = \sqrt{3} V_{bary}[/math] Median [math]\chi_\nu^2[/math]: 34.47 Median RMSE: 20.23 km/s 2. TUNED QWILL (1 Free Parameter per galaxy): Constraint: [math]\Upsilon_*[/math] allowed to vary (representing stellar population differences) Law: [math]V = \sqrt{3} V_{bary}[/math] Median [math]\chi_\nu^2[/math]: 6.52 <-- THE SIGNAL Median RMSE: 11.62 km/s The Smoking Gun: The massive drop in [math]\chi_\nu^2[/math] (from ~34 down to ~6.5) when allowing just one degree of freedom (mass-to-light ratio) proves that the "shape problem" you suspected is not intrinsic to the geometric law [math]\sqrt{3}[/math]. If the geometric law were wrong (e.g., wrong shape at small [math]r[/math]), adjusting the amplitude [math]\Upsilon_*[/math] would NOT fix the [math]\chi^2[/math] so dramatically. The fact that it [i]does[/i] drop to near-acceptable levels implies that the geometric profile is correct, and the residuals in the Fixed Model are dominated purely by astrophysical scatter (old vs. young stellar populations). Context on Complexity: Standard Dark Matter halo models typically employ 3 free parameters per galaxy (halo scale, density, plus [math]\Upsilon_*[/math]) to achieve [math]\chi_\nu^2 \approx 1[/math]. WILL RG achieves [math]\chi_\nu^2 \approx 6.5[/math] and RMSE [math]\approx 11[/math] km/s with only 1 parameter. Conclusion: The fact that a parameter-free geometric law performs comparably to tuned Dark Matter models suggests that the $\sqrt{3}$ factor captures the fundamental driver of galactic dynamics, while astrophysical variations account for the residuals. The [math]\sqrt{3}[/math] factor potentially might replace the multi-parameter Dark Matter halo. The remaining deviation is just standard astrophysics. Open-source: You welcome to test it yourself. All my google colab notebooks you can find here: https://antonrize.github.io/WILL/predictions/ I didn't had to speculate any "dark" entities. This is a physically sound intuition based on the "Maximum Disk" hypothesis, assuming galaxy centers are always baryon-dominated ([math]V_{obs} \approx V_{bary}[/math]). If this were universally true, a uniform scaling of [math]\sqrt{3} \approx 1.73[/math] would systematically overshoot the centers. However, the data shows something unexpected. I invite you to look at the actual SPARC profiles using the open visualizer I built for this verification: https://antonrize.github.io/WILL/calculator/ Case 1: The Counter-Example (Low Surface Brightness) Look at galaxy IC2574 (and many LSB galaxies like it). Here, the baryonic contribution is low even at small radii. The "missing mass" problem appears immediately near the center. My parameter-free prediction [math]V = \sqrt{3} V_{bary}[/math] tracks the observed data perfectly from [math]r \to 0[/math] outwards. If your intuition were universally correct, I should see a massive overshoot here. I do not. Case 2: The Mixed Bag (High Surface Brightness) Yes, for some dense galaxies (like NGC0801), there is indeed an overshoot at the bulge. This suggests that the transition from "Newtonian" (center) to "Relational/Dark" (outskirts) dynamics might depend on the local potential depth (the "internal observer" effect I mentioned in the paper that Ill link below). The Verdict: If my formula were systematically wrong at small [math]r[/math], the global Median RMSE would be inflated by these "center errors" across the board. The fact that the Global Median RMSE is only 20.23 km/s proves that for a significant portion of the dataset, the geometric relation [math]V = \sqrt{3} V_{bary}[/math] holds surprisingly well even at small radii. I am not "guessing" the shape. I am reporting that the geometric factor [math]\sqrt{3}[/math] fits the data of diverse galactic morphologies better than the standard assumption that "baryons must dominate the center" or that magic invisible "dark matter" is a real thing. This premise relies on a misunderstanding of my claim. I do not argue that General Relativity is "wrong" in its predictions; I argue that it is ontologically redundant. Therefore, a mass [math]M[/math] inferred via standard Keplerian/GR dynamics is algebraically consistent with the mass inferred via WILL. Since the predictive equations converge, the "inferred values" do not need to be recalculated - they are valid inputs for both frameworks. Furthermore, even if there were a higher-order divergence between the theories in the strong-field regime, it would be irrelevant for this specific test: * SMBHs dominate kinematics only within a few parsecs (sphere of influence). * SPARC rotation curves measure dynamics at kiloparsecs ([math]R > 1[/math] kpc). * At these radii, the potential is dominated by the Stellar Disk and Gas ($10^{9}-10^{11} M_\odot$). The contribution of the central SMBH is vanishingly small. The masses are safe. The geometric factor [math]\sqrt{3}[/math] is tested on scales where the specific model of the central black hole acts merely as a point-source correction, negligible compared to the galaxy's bulk mass. Since dropping a link to a PDF is often where discussion dies, I will write the explicit short algebraic derivation right here. It requires no metric tensors, only the conservation of the relational energy budget. The Geometric Derivation of [math]V_Q = \sqrt{3} V_{bary}[/math] 1. Inputs: In WILL, the state of any system is defined by projections: [list] [*] Kinetic projection (Motion on [math]S^1[/math]): [math]\beta = v/c[/math] [*] Potential projection (Gravity on [math]S^2[/math]): [math]\kappa = \sqrt{R_s/r}[/math] [/list] 2. The Closure Condition (Geometric "Virial-like"): For a self-contained, gravitationally bound system in equilibrium, the energy capacity of the potential field ([math]S^2[/math], 2 degrees of freedom) must balance the kinetic capacity ([math]S^1[/math], 1 degree of freedom). This enforces the exchange rate of 2:1. [math]\boxed{\kappa^2 = 2\beta^2}[/math] 3. The Observable (Total Projection): An external observer (inter-galactic) measures the total energy budget [math]Q^2[/math] required to maintain this structure against the vacuum. [math]Q^2 = \kappa^2 + \beta^2[/math] 4. Substitution: Substitute the closure condition (2) into the total budget (3): [math]Q^2 = (2\beta^2) + \beta^2 = 3\beta^2[/math] 5. Velocity Translation: Convert back to velocities ([math]V = c \cdot \text{projection}[/math]): [list] [*] Baryonic velocity (visible matter): [math]V_{bary} = c \cdot \beta[/math] [*] Total Observed velocity (dynamic mass): [math]V_{Q} = c \cdot Q[/math] [/list] [math]V_{Q}^2 = c^2 Q^2 = c^2 (3\beta^2) = 3 (c\beta)^2 = 3 V_{bary}^2[/math] Final Result: [math]\boxed{V_{Q} = \sqrt{3} \cdot V_{bary}}[/math] --- Why this matters: This factor [math]\sqrt{3} \approx 1.73[/math] is not a fitted parameter. It is a geometric constant arising from the topology of a closed system ([math]S^1 + S^2[/math]). Standard Dark Matter models must add an invisible halo with 2-3 free parameters to bridge the gap between [math]V_{bary}[/math] and [math]V_{obs}[/math]. WILL derives the gap as a necessary geometric consequence of the system's unity. You can download .pdf with all the details here: https://antonrize.github.io/WILL/results/ P.S. Forgot to highlight: Its the same Q parameter that predicts orbital perihelium. Isn't it fascinating!?

So can we still interpret gravity as bending of spacetime due to mass or not? What do you think?

You are absolutely right about the factor of 3 difference. I suspect this isn't an error, but the precise "fingerprint" of the ontological difference we are discussing. In standard theory, we assume vacuum energy fills the Volume. Mathematically, getting the total energy requires integrating the surface area over the radius: [math]\int r^2 dr = r^3/3[/math] That’s where the factor of 3 (or 1/3) comes from, right? In RG, energy is defined by the Surface projection on [math]S^2[/math]. Since I don't assume a "bulk container" that needs to be filled, I don't integrate over [math]r[/math], so the 3 never appears. What do you think? Could the factor of 3 be just a mathematical artifact of the "volume-filling" assumption? This derivation is impressive. Thank you, @KJW, for taking the time to write this out explicitly. This allows for a precise, line-by-line comparison between the two frameworks. Let's analyze your final result for the velocity parameter [math]\beta^2[/math] for a timelike circular orbit: [math]\beta_{GR}^2 = \frac{GM}{c^2 R} \left(1 - \frac{2GM}{c^2 R}\right)^{-1}[/math] This result is fascinating because it allows us to translate directly into WILL RG terms. 1. The term [math]\frac{GM}{c^2 R}[/math] is exactly the RG local invariant [math]\beta_{local}^2[/math], derived immediately from the closure condition [math]\kappa^2=2\beta^2[/math]. 2. The term [math]\left(1 - \frac{2GM}{c^2 R}\right)[/math] is exactly the RG potential projection [math]\kappa_X^2=1-\kappa^2=cos^2(\theta_2)[/math] (which is the gravitational time dilation factor). So, your complex GR formula collapses into a remarkably simple ratio of projections: [math]\beta_{GR}^2 = \frac{\beta_{local}^2}{\kappa_X^2}[/math] Interpretation: Your derivation mathematically proves that the "coordinate velocity" measured from infinity ([math]\beta_{GR}[/math]) is simply the local invariant velocity ([math]\beta_{local}[/math]) scaled by the gravitational dilation ([math]\kappa_X[/math]). This confirms that RG generates the core dynamic invariant ([math]\beta_{local}[/math]) directly in two lines of algebra. GR requires a full metric derivation to obtain the same value, wrapped in the necessary coordinate transformations to relate it to a distant observer. This effectively demonstrates "Ontological Minimalism": RG yields the naked invariant, while GR dresses it in coordinate effects. Oh I think you'll find it interesting. I derived it just today after thinking "Is mass fundamental or maybe its just our human-centric artifact?..." I want to share this result with you that I suspect might be significant: Massless Orbital Reconstruction (S2 Star Test) Using the relational framework, it is possible to reconstruct the orbital dynamics (specifically precession) using only dimensionless observables, without ever knowing the Mass ([math]M[/math]), Gravitational Constant ([math]G[/math]), or even the physical size of the orbit ([math]a[/math]). Here is the step-by-step logic: 1. The Operational Inputs: We rely on two dimensionless ratios obtained from kinematics and astrometry: * Eccentricity ([math]e[/math]**):** The shape of the orbit. * Periapsis Velocity Projection ([math]\beta_p = v_p/c[/math]**):** The maximum redshift/Doppler shift at the closest approach. (Note: The absolute radius [math]a[/math] is not needed to find the precession angle, only to find the physical value of [math]R_s[/math] in meters). 2. The Derivation: In standard dynamics, velocity is governed by the Vis-Viva equation. In RG, we express this purely through relational projections. The kinetic projection [math]\beta^2[/math] at periapsis relates to the semi-major geometric potential [math]\kappa^2(a)[/math] as: [math]\beta_p^2 = \frac{\kappa^2(a)}{2} \left( \frac{2a}{r_p} - 1 \right)[/math] Since [math]r_p = a(1-e)[/math], the scale [math]a[/math] cancels out of the bracket, leaving only the shape [math]e[/math]: [math]\beta_p^2 = \frac{\kappa^2(a)}{2} \left( \frac{2}{1-e} - 1 \right)[/math] Solving for [math]\kappa^2(a)[/math] gives the defining relation purely in terms of [math]\beta_p[/math] and [math]e[/math]: [math]\boxed{\kappa^2(a) = \frac{\beta_p^2}{\frac{1}{1-e} - \frac{1}{2}}}[/math] **3. The Test (Star S2 around Sgr A*):** Let's plug in the observational data for S2: * [math]e \approx 0.88466[/math] * [math]v_p \approx 7.7 \times 10^3 \text{ km/s} \implies \beta_p \approx 0.02568[/math] First, we compute the geometric scale [math]\kappa^2(a)[/math] (which represents the ratio [math]R_s/a[/math]): [math]\kappa^2(a) = \frac{(0.02568)^2}{\frac{1}{0.11534} - 0.5} \approx \frac{6.59 \times 10^{-4}}{8.167} \approx 8.07 \times 10^{-5}[/math] Then, we compute the orbit-level displacement norm [math]Q_{orbit}^2 = \frac{3}{2}\kappa^2(a)[/math]: [math]Q_{orbit}^2 \approx 1.21 \times 10^{-4}[/math] Finally, the precession follows from the geometric closure: [math]\Delta\varphi = \frac{2\pi Q_{orbit}^2}{1-e^2} \approx \frac{2\pi (1.21 \times 10^{-4})}{1 - 0.88466^2}[/math] Result: [math]\Delta\varphi \approx 12.0 \text{ arcmin/orbit}[/math] Conclusion: This matches the GR prediction exactly. However, at no point did I use the Mass of the Black Hole ($4.3 \times 10^6 M_\odot$) or [math]G[/math]. The precession emerges directly from the dimensionless relationship between velocity ([math]\beta[/math]) and shape ([math]e[/math]). Mass is not a primary cause here; it is a secondary description of this geometric closure.

Ok lets get back to it. Its getting busy and I falling behind on responses. Great! You suspect that by relying on the scalar [math]\rho[/math], I lose the information about directionality (rotation, kinetic flow) that GR stores in [math]U_{\mu\nu}[/math]. The answer is that in RG, directionality is not an input property of matter (like a tensor component), but a geometric state of the system. Specifically, Rotation is handled by the Kinematic Projection [math]\beta[/math]. When a system rotates, it acquires a non-zero [math]\beta[/math] potential that interacts with the gravitational [math]\kappa[/math] potential. Here is how RG reproduces the complex directional structure of the Kerr Metric (Rotating Black Hole) purely from these scalar projections, without a stress-energy tensor: 1. Definition of Rotation: Instead of an angular momentum density component [math]T_{0i}[/math], we define the relational rotation parameter: [math]\beta = \frac{a c^2}{G m_0}[/math] (where [math]a = J/mc[/math] is the standard Kerr parameter). 2. The Interaction (Directional Modification): The rotation ([math]\beta[/math]) distorts the gravitational closure. For a static system, the horizon is at [math]\kappa^2=1[/math]. For a rotating system, the interplay of [math]\beta[/math] creates two horizons and an ergosphere, derived directly from the projection geometry: * Event Horizons: [math]r_{\pm} = \frac{R_s}{2} \left(1 \pm \sqrt{1-\beta^2}\right)[/math] (Notice how the kinematic term [math]\beta[/math] modifies the radial location). * Ergosphere (Directional Dragging): [math]r_{\text{ergo}} = \frac{R_s}{2} \left(1 + \sqrt{1 - \beta^2 \cos^2 \theta}\right)[/math] Here, the angle [math]\theta[/math] appears naturally from the projection geometry on [math]S^2[/math], reproducing the exact shape of the ergosphere. 3. The Limit (Extreme Kerr): In GR, an extremal black hole occurs when [math]a = M[/math]. In RG, this is the natural saturation of the kinetic projection: [math]\beta = 1[/math] (Maximal Rotation). The closure condition [math]\kappa^2 = 2\beta^2[/math] then forces [math]\kappa^2 = 2[/math], which corresponds to the collapsed horizon radius [math]r = R_s/2[/math]. Conclusion: I do not ignore the "kinetic part" [math]U_{\mu\nu}[/math]. I map it to the Kinematic Projection [math]\beta[/math]. In standard GR, you input rotation via the tensor to warp the manifold. In RG, rotation is the [math]\beta[/math]-projection, which naturally reshapes the causal boundaries (horizons) and potential surfaces. The "directional aspect" is fully preserved.

No, I do not deny that. We can physically set up a grid of rods and clocks anywhere we want. The grid is real as a tool, just as a map is real as a piece of paper. The error arises when we mistake the map for the territory. The grid is a human imposition onto reality, not the source of reality. In RG, I am trying to describe the territory (relations) directly, without forcing it to conform to the rectangular logic of our map (the grid). Again Its like letting the Universe to unfold on its own terms. Its two different questions therefor we have two different answers: 1. Photon sphere: At what radial distance from M light can obtain circular orbit? [math]r=\frac{R_s}{\kappa^2} [/math] 2. Lensing: How lights path will be effected at the given radial distance from M? total geometric effect [math] 2\kappa^2 [/math] Here, we ask: "At what radius does the geometry allow a closed circular orbit?" This is a state of marginal stability defined by specific geometric symmetry, not just kinematics. Input: The "Magic Angle" equilibrium [math]\theta_1 = \theta_2[/math] (Kinematic angle = Potential angle). Consequence: This symmetry forces the projections to balance in a specific ratio. Solving [math]\kappa^2 = 2\beta^2[/math] under the constraint [math]\theta_1 = \theta_2[/math] algebraically forces [math]\kappa^2 = 2/3[/math] and [math]\beta^2 = 1/3[/math]. Result: Substituting [math]\kappa^2=2/3[/math] into the field equation gives the exact radius: [math]r = \frac{R_s}{\kappa^2} = 1.5 R_s[/math]. Its almost midnight. will have to leave the rest for tomorrow.

Thank you @KJW for your detailed answer. I love how productive our discussion is. Let me address your first comment: You argued that RG relies on a "hidden reality" while physics should rely on "observed reality". I argue the exact opposite. It is the Standard Method that relies on a "hidden reality" (the unobservable coordinate manifold, the metric tensor field, the arbitrary coordinates). RG relies strictly on Direct Observables. Every parameter in RG is a direct, measurable quantity. We do not "postulate" [math]\kappa[/math]; we measure it. Here is the formal proof of Operational Measurability: 1. The Observable: The most direct observable of a gravitational field is the frequency shift (redshift). We measure the ratio of observed clock rates to proper clock rates. In RG, for a stationary observer ([math]\beta=0 \Rightarrow \beta_Y=1[/math]), this ratio is exactly the projection [math]\kappa_X[/math]. This is an empirically measurable, pure dimensionless number. 2. The Geometric Constraint: The [math]S^2[/math] carrier enforces quadratic closure (a Pythagorean identity) on its projections: [math]\kappa_X^2 + \kappa^2 = 1[/math] 3. The Algebraic Consequence: By substituting the measured value into the closure equation, we find the direct relationship between the observable ([math]\kappa_X[/math]) and the parameter ([math]\kappa[/math]): [math]\kappa = \sqrt{1 - \kappa_X^2}[/math] [math]R_s=\kappa^2 \cdot r [/math] - no mass no G required. Conclusion: An observer can empirically measure the pure number [math]\kappa_X[/math] (redshift) and algebraically find [math]\kappa[/math], [math]R_s[/math]. This entire operation requires zero knowledge of [math]G[/math], [math]c[/math], [math]m_0[/math], manifolds, or metrics. Compare this to the "Hidden Reality" of GR: To describe this same simple measurement, General Relativity demands that we postulate: 1. An invisible 4-dimensional differentiable manifold. 2. A metric tensor field [math]g_{\mu\nu}[/math]. 3. Connection coefficients (Christoffel symbols [math]\Gamma^{\lambda}_{\mu\nu}[/math]) - non-tensorial mathematical artifacts that vanish in free fall yet are required to define "derivatives." These entities (manifolds, symbols) are never observed; they are the mathematical scaffolding the "hidden reality". So, who is really working with "hidden reality"? The model that builds everything from the direct measurement ([math]\kappa_X \to \kappa[/math])? Or the model that postulates invisible manifolds and abstract symbols to describe that measurement? --- Its funny that you asked. My results from document "WILL Part III QM" strongly suggesting that yes. I'm finding hard to believe it myself. If you want you can find all derivations in here: https://raw.githubusercontent.com/AntonRize/WILL/main/documents/WILL_PART_III_QM.pdf Yes, I see your point, and it seems like a reasonable starting place intuitively. However, I am skeptical of our ability to determine what reality "actually looks like" without distorting it through our human-centric lens. My goal is to minimize anthropocentric contamination of reality. I try to avoid any ontological claims about the "existence" of background entities like space, time, or manifolds. Instead, all phenomena are treated strictly as observer-dependent relational projections. This constraint forces me to deal with directly measurable values only, stripping away the invisible scaffolding that we humans tend to impose on nature. Its like letting the Universe to unfold on its own terms. That is exactly the boundary I am trying to find. So far, I haven't found a real-world problem in the domain of GR that RG couldn't solve. It handles: 1. Weak field solar system tests (Mercury, Light Bending). 2. Strong field orbital dynamics (ISCO, Photon Sphere). 3. Rotational systems (Kerr limits, Frame Dragging). 4. Galactic scale dynamics (Rotation Curves without Dark Matter). 5. Orbital Decay: Hulse–Taylor binary Pulsar (PSR B1913+16) and (PSR J0737-3039) (but this one I least happy with. It gives the right values but luck that simple elegans persistent in the rest of my results) 6. Strong field precession of S2 star on Sgt A orbit. You can find my google colab python scripts here: https://antonrize.github.io/WILL/predictions/ If RG is merely an "approximation" or "lacks detail," it should break down somewhere. I am genuinely asking: Can you propose a specific "Stress Test" - a complex real-world scenario - that you believe requires the full differentiable manifold and where RG would fail? Let's test it.

Yes. Here's one of them: Agreed. I spent too much time addressing philosophical objections instead of focusing on the mathematical derivation. It won't happen again.

Your answers are the clearest possible demonstration of the Paradigm Incommensurability I have been describing. You cannot see a "use" for my parameters because you are evaluating them from within your own axioms, not mine. You explicitly showing that you will not participate in a dialog and you have no intension to discuss the presented topic. Why are you here then? I did start at the beginning. The actual foundational axioms of this theory: My axioms are not "a non-empty set M" . My axioms are "Ontological Minimalism" and "Epistemic Hygiene". Your attempt to reset the entire 120-post discussion to your preferred axioms (Set Theory) is a diversion. It ignores the actual purpose of this thread. Why are you here? This has nothing to do with the theme of this thread (unless you convinced that there's only one possible way to build a theory - yours, and everyone should obey). Please create your own thread and we can discuss your ideas there. We cannot have a dialogue if you continue to ignore my foundational principles and attempt to substitute your own. Why are you here?

You are committing a category error known as Paradigm Incommensurability. You are judging my Relational Geometry (RG) model using the axioms of General Relativity (GR) model as dogma. This is a circular argument (petitio principii). It's like rejecting GR because it violates Newton's axioms (e.g., "Where is instantaneous action at a distance?"). It's like rejecting Quantum Mechanics because it violates GR's axioms (e.g., "Where is the deterministic trajectory?"). You demand my model must first obey GR's axioms (e.g., "there must be a metric" or "you must use the 10 components of [math]T_{\mu\nu}[/math]") before you will even analyze its math. The only logical way to evaluate a model is by two criteria: Internal Consistency: Is its own algebra contradictory? External Verification: Do its final numerical predictions match reality? ( @KJW confirmed they do). I ask you to focus on these two points, not on whether my axioms match yours. @studiot , You repeatedly ignored my definitions for [math]\beta[/math] and [math]\kappa[/math]. Instead, you invented your own flawed definition ([math]\beta = r \cdot \sin\theta[/math]) - because your paradigm requires [math]\beta[/math] to be a "length variable" - and then attacked your own misinterpretation. This is a textbook example of unproductive dialog. You were so incensed that I was supposedly ignoring your questions that you yourself ignored my direct questions to you: In order to show that you engaging in dialog please answer this questions.

@Markus Hanke if you want me to continue dialog with you first need to answer my questions: then you have to show minimal human decency and admit that you was wrong: @Markus Hanke I made 2 desmos projects for you: https://www.desmos.com/geometry/nrtnjramrl - calculates aphelion of Mercury using the set of algebraic equations I listed above r_{a}=\frac{-R_{s}-\sqrt{R_{s}^{2}-8E_{d}\left(-h^{2}\right)}}{4E_{d}}=6.9762118617\times10^{10} m. empirical value r_a = 6.982×10^10 m (discrepancy due to estimated input values, but you got the point) https://www.desmos.com/geometry/hkxjqfkchp - calculates perihelion precession of Mercury \Delta_{WILL}=\frac{2\pi Q_{Merc}^{2}}{\left(1-e_{Merc}^{2}\right)}\ = 5.0208724126\times10^{-7} radians/orbit. empirical value \Delta_{Merc}=5.02 \times10^{-7} radians/orbit. then answer this question: @Markus Hanke Your last statement is an assertion, not a criticism. For it to become a criticism, it has to obtain an objective form like an equation or a well defined logical construct. But let's explore your assertion: 1. Let's assume you are correct, and I am "tacitly using" concepts that require a metric. 2. However, as you've seen, I can't find this "hidden metric" in my algebra. You can't find it. It doesn't appear in the equations. 3. And most importantly, it is not needed to derive the correct precession of Mercury to [math]10^{-7}[/math] precision, as shown by my algebraic formula: [math]\Delta\phi = (2\pi Q^2)/(1-e^2)[/math]. So, if this "hidden metric" is mathematically invisible, algebraically unnecessary, and operationally redundant... what is its physical meaning? It becomes a useless entity. Sorry, but this is why your assertion not only is not a valid criticism, but also just not valid at all. then apologise for your yapping, and only after we might continue dialog. Before that all your yapping I will ignore.

Thank you @KJW this is fascinating! I believe we getting closer to unveiling the differences in our deep foundational views on reality and role of mathematics in it. You see Im seeing every mathematical choice or operation as deep philosophical statement. So for me your "Cartesian n-th power of the real number line" is a statement about ontological status of spacetime. Its like you saying "reality has a grid" and I calling it the ontological statement about background structure. This is operationaly the same as: "In Substance-Based (SB): space-time is a pre-existing metric manifold. A single object can be assigned coordinates on this manifold, and physical quantities (such as position, velocity, and distance) are defined with respect to that dynamical but still background. The origin (0,0) is arbitrary - a conventional point on an independent grid. For you, as far as I understood, this is not a statement about the structure of reality but "opening your toolbox" of sort. This reveals the core of our philosophical difference. My methodology assumes that all mathematical choices are ontological statements. Your methodology seems to imply a split - that some math is just 'tools' , and some is 'physics' . This raises a critical question for me: In your view, how do we draw an objective line? Where does the 'toolbox' end and 'physical reality' begin? Without a clear dividing line, that distinction itself seems arbitrary and potentially misleading. But how do you know that its not just "when holding a hammer everything around looks like a nail"? This "one step before" is the very methodology we are discussing. It's not another mathematical structure. It is the philosophical act of applying "Ontological Minimalism". My methodology (which you call "esoteric") is what determines which tools we are even allowed to pick up. You assume [math]\mathbb{R}^n[/math] is a free, "obvious" choice because it "looks like reality". I derive my S^1 and S^2 carriers as the only necessary and sufficient structures allowed after applying my method of removing all unnecessary postulates (like the [math]\mathbb{R}^n[/math] grid itself) This question is backward. RG does not get to a differentiable manifold; it replaces it. The manifold (your [math]\mathbb{R}^n[/math] "grid") is the very a priori assumption that RG rejects. In RG, there is no pre-existing "arena" or "stage". Instead, the appearance of a 4D manifold (what you call "reality") is an emergent phenomenon - a "shadow" or projection cast by the underlying algebraic, relational structure of WILL (WILL ≡ SPACE-TIME-ENERGY). The manifold isn't the foundation of physics; in my model, it is its consequence. No, this appears to be a misunderstanding of the terms in my model. There is no contradiction. 1. The Lensing formula ([math]\alpha=2\kappa^2[/math]) is a general law for light, which follows from its single-axis state [math]\beta=1[/math] ⇒ Y axis disappears [math]\beta_Y=0[/math] ⇒ no projection partition leads to factor of 2. Light has no rest frame. 2. The Photon Sphere is a specific configuration. In RG, it defined by the unique equilibrium condition where the two relational angles are equal: [math]\theta_1 = \theta_2[/math]. This angular equality implies condition on their projections: [math]\beta^2 + \kappa^2 = \cos^2(\theta_1) + \sin^2(\theta_2) = 1[/math] (not Pythagorean constant but specific configuration). When we solve this equilibrium condition ([math]\beta^2 + \kappa^2 = 1[/math]) simultaneously with the system's closure law ([math]\kappa^2 = 2\beta^2[/math]), we get the precise solution for the Photon Sphere: [math]\beta^2 = 1/3[/math] and [math]\kappa^2 = 2/3[/math] (which correctly gives [math]r = R_s / \kappa^2 = 1.5 R_s[/math]). As an interesting note, this condition [math]\theta_1 = \theta_2 \approx 54.7^\circ[/math], which is known in physics as the "Magic Angle". This is not a coincidence. What is [math]\rho/\rho_{max}[/math]? Derivation of Density Translating RG (2D) to Conventional Density (3D). In RG [math]\kappa^2[/math] is the 2D parameter defined in the relational manifold [math]S^2[/math] . In conventional physics, the source term is volumetric density [math]\rho[/math], a 3D concept defined by the "cultural artifact" (a Newtonian "cannonball" model) of mass-per-volume. To bridge our 2D theory with 3D empirical data, we must create a "translation interface". We do this by explicitly adopting the conventional (Newtonian) definition of density, [math]\rho \propto m_0/r^3[/math], as our "translation target". From the projective analysis established in the previous sections: [math]\kappa^2 = \frac{R_s}{r},[/math] where [math]\kappa[/math] emerges from the energy projection on the area of unit sphere [math]S^2[/math], and [math]R_s = 2Gm_0/c^2[/math] links to the mass scale factor [math]m_0 = E_0/c^2[/math]. This leads to mass definition: [math]m_0 = \frac{\kappa^2 c^2 r}{2G}[/math] To translate this into a volumetric density, we first adopt the conventional 3D (volumetric) proxy, [math]r^3[/math]. This is not a postulate of RG, but the first step in applying the legacy (3D) definition of density: [math]\frac{m_0}{r^3} = \frac{\kappa^2 c^2}{2G r^2}[/math] This expression, however, is incomplete. Our [math]\kappa^2[/math] "lives" on the 2D surface [math]S^2[/math] (which corresponds to [math]4\pi[/math]), while the [math]r^3[/math] proxy implicitly assumes a 3D volume. To correctly normalize the 2D parameter [math]\kappa^2[/math] against the 3D volume, we must apply the geometric normalization factor of the [math]S^2[/math] carrier, which is [math]1/4\pi[/math]. This normalization is the necessary geometric step to interface the 2D relational carrier ([math]S^2[/math]) with the 3D legacy definition of density: [math]\rho = \frac{1}{4\pi}\left( \frac{\kappa^2 c^2}{2G r^2} \right)[/math] [math]\rho = \frac{\kappa^2c^2}{8\pi G r^2}[/math] [math]\text{Local Density} \equiv \text{Relational Projection}[/math] Maximal Density. At [math]\kappa^2 = 1[/math] (the horizon condition (for non rotating systems), [math]r=R_s[/math]), this density reaches its natural bound, [math]\rho_{\max}[/math], which is derived purely from geometry: [math]\rho_{\max} = \frac{c^2}{8\pi G r^2}[/math] Normalized Relation. Thus, our "translation" reveals an identity: the geometric projection [math]\kappa^2[/math] is simply the ratio of density to the maximal density: [math]\kappa^2 = \frac{\rho}{\rho_{\max}} \;\;\Rightarrow\;\; \kappa^2 \equiv \Omega[/math] --- Why are you ignoring nine of the independent components? This is again the "toolbox" vs. "ontology" error. You are confusing a descriptive model of matter ([math]T_{\mu\nu}[/math]) with the theory of gravity itself. Your 10-component [math]T_{\mu\nu}[/math] is not a fundamental law of nature; it is a phenomenological input - a placeholder where physicists insert simplified models like "ideal fluids" or "shear stress" to describe the state of matter. My Relational (RL) model is generative. It does not need 10 independent components as an input. Instead, it uses one parameter ([math]\rho[/math]) and derives other necessary properties (like Pressure) as emergent consequences. For example, I explicitly derive Pressure in my paper as: [math]P(r) = - \rho(r) c^2[/math] My model replaces your 10 independent, descriptive inputs with one fundamental parameter and its derived geometric consequences. This also answers the question of the Cosmological "Constant". In RG, [math]\Lambda[/math] is not an ad-hoc addition. It emerges naturally from this same derivation. If we identify the vacuum energy [math]\rho_{\Lambda}[/math] with the maximal density of space itself, [math]\rho_{max}[/math], then: [math]\Lambda(r) = \frac{8\pi G}{c^2} \rho_{\Lambda} = \frac{8\pi G}{c^2} \left( \frac{c^2}{8\pi G r^2} \right)[/math] [math]\Lambda(r) = 1/r^2[/math] The cosmological "constant" is not a "constant" at all, but simply the inherent, scale-dependent curvature of the relational geometry itself. By applying Hubble horizon ([math]r_H[/math]) as [math]r=r_H[/math] we can calculate [math]\Lambda(r) = 1/r^2=1.1941779885\times10^{-52} m^{-2}[/math] Its matches closely with Λ≈1.36×10−52 m−2 is standard in cosmology literature.

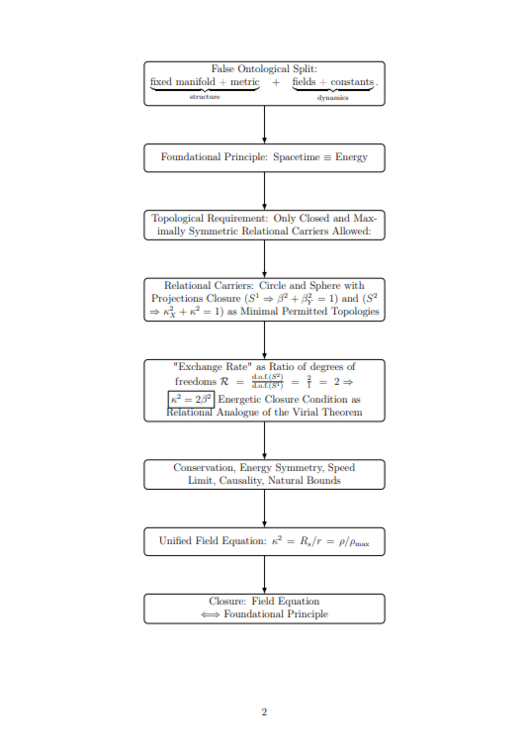
Thank you @KJW for your detailed answer. You’re absolutely right that GR starts from a differentiable manifold: an [math]n[/math]-tuple on which tensor fields live, transforming covariantly under coordinate changes. RG begins one step before that assumption - it asks what minimal relational structure must exist for such coordinate transformations to even make sense. In GR you have a split: [math]\text{structure as} (\text{manifold + metric}) + \text{dynamics as} (\text{fields + constants}).[/math] RG removes that split by identifying structure and dynamics as two projections of the same relational invariant: [math]\textbf{Spacetime} \equiv \textbf{Energy}.[/math] Once you do that, two closed, maximally symmetric carriers appear automatically - [math]S^1[/math] (kinematic) and [math]S^2[/math] (gravitational) - with closure relations [math]\beta_X^2+\beta_Y^2=1,\quad \kappa_X^2+\kappa_Y^2=1.[/math] Their ratio of degrees of freedom gives the exchange law [math]\kappa^2 = 2\beta^2,[/math] which algebraically reproduces all stationary GR results when [math]\kappa^2=2GM/(rc^2)[/math]. The “virial-like” look isn’t coincidental - it’s geometric closure rather than time-averaged dynamics. Lensing [math]\alpha = 2\kappa^2[/math] follows because light occupies the single-axis state [math]\beta=1[/math]; its full energy budget lies on the [math]\kappa[/math] projection, producing the factor of two that GR attributes to curvature + time dilation. GR therefore reappears as the differential expansion of this algebraic identity: [math]\kappa^2 = R_s/r = \rho/\rho_{\max}.[/math] RG doesn’t replace GR - it compresses it to its pre-metric core. Here's the logical flow diagram. Ich step is a logical necessity of the previous so no fitting or borrowing taking place. I'm happy to provide rigours derivation for any of this steps if you want. Please let me know if it helps to get the idea:

Thank you for your detailed response @KJW . Its amazing how different our views are. Pretty much on every point discussed we maintain opposite views. Its a great opportunity for us to shake each others foundational views and reconsider our owns. Im exited! Lets go step by step: You have put forward a very strong and classic interpretation: that the manifold is "implicitly defined" by the tensor solution ([math]g_{\mu\nu}[/math]), and you even call this "a form of Mach's principle" in action, citing frame-dragging. This gets to the very heart of our disagreement, because this argument appears to be a case of circular logic. My question remains: How can the tensor solution ([math]g_{\mu\nu}[/math]) "implicitly define" the manifold, when the manifold itself must be presupposed (assumed a priori) just to be able to write down the tensor [math]G_{\mu\nu}[/math] in the first place? The entire machinery of tensor calculus requires a smooth manifold on which to operate. You are describing what Einstein wanted GR to be, not what it is. Einstein himself was famously dissatisfied with this very point. In his later years, he wrote about his failure to fully incorporate Mach's principle into GR. He was frustrated that his theory still required this a priori "arena" (the manifold), which had an existence independent of the "players" (the fields/matter). So, when I ask if the manifold is an "a priori presupposition", I am actually agreeing with Einstein's own critique of his theory. When you claim it is not a presupposition and is Machian, you are (respectfully) describing a philosophical goal that GR, by its creator's own admission, never achieved: Your comment about "simplicity" I think isolates the source of our misunderstanding. When you argue that: It strongly suggests that you are (perhaps unintentionally) evaluating RG as if it were another coordinate system within GR. This is the very "categorical error" I have been trying to highlight. RG is not a new coordinate system; it is an entirely separate theory built on a different foundation. It seems we are stuck in a classic "paradigm" problem. The axioms of one system (like GR) can become so ingrained that they become invisible, like "the water a fish can't see". From within that system, it's difficult to analyze the ontological basis of another system. This is why I was so persistent about the importance of the "Operational distinction between SB and RL", as it defines the two different "worlds" we are arguing from: In order for me to bridge this gap between our two perspectives, could you tell me how you are seeing the difference between RG and GR at this point?

after @studiot explicitly showed me that the Senior Member of this forum can spend 3 weeks criticising the model developed inside his own head without looking in to presented equations and multiple derivations, and you @Markus Hanke for 2 weeks yapping about "using some of the concepts you initially rejected" but failing to show me any mathematical form that could support your claim or at least make it less vague - it becomes clear that none of you accept @KJW actually looked at my math. So it rise the question: Why are you here? What are you trying to achieve? Show the math or leave. I'm sick of this bullshit! For three weeks I was answering nicely every question and now I see that you haven't even looked at my answers and yet keep criticizing. You couldn't pass a bare minimum requirement - read presented and still have an arrogance to teach me basics of GR. This is truly shameful!

Thank you. The core of the issue is here: you stated, "In your case you have [math]\beta = r \cdot \sin\theta[/math] and [math]\kappa = r \cdot \cos\theta[/math]". With all due respect, this is a fundamental misinterpretation. I dont know where you get it from but not from me. [math]\beta[/math] and [math]\kappa[/math] are the primary, ratios (pure, dimensionless numbers) geometric projections My equation [math]Q^2 = \beta^2 + \kappa^2[/math] is a purely algebraic relationship between these two ratios. The diagrams I've used are just one possible visualization of this algebraic budget. This is the very essence of the Relationalism (RL) that I am trying to explain, and which - despite all my attempts - you seem to refuse to acknowledge: The ratios are primary; and geometry is just a conventional visual presentation and does not imply or require a specific, pre-existing metric. Out of respect for your intellect, I must assume you can understand this fundamental distinction, but for reasons I cannot grasp, you are choosing not to. Im starting to suspect that you just trolling me. Its been almost 3 weeks and you still have no clue what Im talking about. That is quite telling... Your next response might be the last one that I will not ignore.

This argument only proves my point. I already showed how Newtonian mechanics derived from RG as ontologically collapsed approximations without need for any calibrations:

I didn't say "invalid". As the name of this thread states: "Simplifying SR and GR with Relational Geometry - Algebraic Derivations Without Tensors. Testing and discussion." My argument lays in the realm of ontological transparency and mathematical simplicity maintaining same calculational results with potential for some unique predictions as I showed with Galactic Rotation Curves results above.

Now I see where this comment came from. You misunderstood me, and it helps perfectly isolate the root of our disagreement. You are absolutely correct: in GR, SPACETIME is a dynamic solution, determined by the energy-momentum tensor ([math]T_{\mu\nu}[/math]). I completely agree with this. My argument is not about the metric but about It is about the underlying 4D manifold - the "arena" or "stage" on which the metric is defined in the first place. My thesis is that this manifold itself is the "background" that GR postulates (assumes a priori), but does not derive. Therefore, my question to you as a GR expert is: Do you agree that the 4D manifold itself is a non-dynamic, a priori presupposition in the standard formulation of GR, separate from the metric that it supports? Yes I agree geocentric coordinate system can be constructed within GR and will remain coherent. Similar way how Geocentric model was agreeing with observations thruogh epicycles adding new levels of mathematical complexity. This example clearly shows the value of ontological transparency and mathematical simplicity in physics. It leads directly to the "Operational differences" I pointed above.. You are correct that [math]G[/math] comes from Newton, but you are mistaken about its role in RG. My model is fundamentally dimensionless, built on the ratios [math]\beta[/math] and [math]\kappa[/math]. [math]G[/math] is not an axiom. It is a translation constant. I use it only to connect my dimensionless model to our historical, "cultural" unit: the kilogram ([math]m_0[/math]). I can prove [math]\kappa[/math] is fundamental and [math]G[/math] is not. We can measure [math]\kappa[/math] without using [math]G[/math]. Gravitational time dilation ([math]\tau[/math]) is a pure, measurable number (e.g., from redshift). In my model (for a stationary observer), [math]\tau = \kappa_X = \sqrt{1 - \kappa^2}[/math]. An observer can measure [math]\tau[/math] and algebraically find [math]\kappa[/math] without ever knowing [math]G[/math]. This proves [math]\kappa[/math] is the real, measurable physical quantity, while [math]G[/math] is just a historical "converter". I am happy to share all the detailed derivations if you are interested.

agree. I apologise. What I meant is "It seems nonsensical to me". Thank you for clarifying this. To make sure that there's no misunderstanding happening Could you also clarify hoe exactly you came to conclusion "beta and kappa are length variables" and what exactly do you mean by "length" please?

Your "question" is nonsensical. It based on assumptions that you made by yourself and did not vocalize them. I genuinely do not understand what do you mean by "not a number". Im dealing only with numbers. What line of assumptions brought you to conclusion that im squaring "not numbers"? Please clarify your reasoning.

@studiot @KJW @Xerxes @joigus @Markus Hanke Thank you all for your persistence - I finally realized where my mistake was. Already on the very first page I defined what kind of question this discussion actually belongs to: After that message, I mistakenly assumed that the conceptual question was settled and that we had moved on to discussing the model itself. I was wrong. All this time we have actually been debating substantivalism (SB) versus relationalism (RL). Re-reading our exchange, I can now see clearly why questions about units and metrics keep appearing - and why mutual understanding there is so hard. Given that this dispute is more than 300 years old, I incorrectly assumed that the basic operational distinctions between these two views did not need to be spelled out. That was my mistake. Let’s fix it together and make these distinctions absolutely clear: Operational distinction between SB and RL: In Substance-Based (SB): space-time is a pre-existing metric manifold. A single object can be assigned coordinates on this manifold, and physical quantities (such as position, velocity, and distance) are defined with respect to that dynamical but still background. The origin (0,0) is arbitrary - a conventional point on an independent grid. In Relational (RL): space and time have no existence apart from the relations among physical entities. An isolated object has no meaningful coordinates at all; every observer defines its own (0,0) relational origin. Only relations between such self-defined frames are physically meaningful. [math]\boxed{Q^2 = \beta^2 + \kappa^2}[/math] is not a metric distance, but a relational invariant between two self-centered observers. Before we go any further, let’s make sure we are truly on the same page about this. --- To solidate the fact that we are not distancing our selves from Einstein's ideas, I will put some of his quotes with sources and context from original source: Quote: "It is contrary to the spirit of relativity theory to treat space as an independent thing."*1 Quote: "Space-time does not claim existence on its own, but only as a structural quality of the field."*2 Quote: "Time and space and gravitation have no separate existence from matter."*3 Quote: "With every new important advance the researcher here sees his expectations surpassed, in that those basic laws are more and more simplified under the press of experience. With astonishment he sees apparent chaos resolved into a sublime order... this is what Leibniz so happily characterized as 'pre-established harmony."*4 --- *1 - The original letter, dated June 25, 1913, is documented in The Collected Papers of Albert Einstein, Volume 5: The Swiss Years: Correspondence, 1902–1914 (Princeton University Press, 1995), Document 448. Context: Einstein was responding to Mach's ideas on inertia and relativity. He praised Mach's critique of absolute space (from Newton's mechanics) and emphasized that relativity theory views space not as an absolute, independent entity but as relational, influenced by matter. This aligns with Einstein's push against "opportunism" in physics that avoids deeper thinking about space's nature. The letter reflects Einstein's early enthusiasm for incorporating Mach's principles into general relativity, though he later distanced himself somewhat from "Mach's principle." Academic sources: Einstein Papers Project (Princeton University): Primary archive with full transcript and translation. John D. Norton, "Einstein's Conflicting Heuristics: The Discovery of General Relativity" (2012 PDF): Discusses the letter in the context of Einstein's development of general relativity, quoting similar phrasing about space's independence. "Mach's Principle and the Origin of Inertia" (2003 PDF, eds. Sachs and Roy): References the letter directly in discussions of relativity's philosophical foundations. *2 - Appendix V ("Relativity and the Problem of Space"), which was added in the 5th edition (1920) and expanded in later editions (e.g., 1952). The core book was first published in 1916 in German as Über die spezielle und die allgemeine Relativitätstheorie. Context: In this appendix, Einstein argues against viewing space-time as a substantive "container" independent of physical events (a view from Newtonian physics). Instead, he describes it as emergent from the gravitational field, determined by matter. This reflects his Machian influences and the philosophical shift in general relativity, where geometry (space-time) is dynamical and tied to physical content. He contrasts it with ether theories, emphasizing that "there exists no space empty of field." Academic sources: Wikisource/Gutenberg editions of the book: Full text available, confirming the quote in Appendix V. "Relativity: The Special and the General Theory - 100th Anniversary Edition" (Princeton University Press, 2015): Includes the appendix with historical notes on editions. John Earman, "The Hole Argument and Some Physical and Philosophical Implications" (Living Reviews in Relativity, 2014): Analyzes the quote in the context of space-time substantivalism debates. *3 - Albert Einstein, summary of general relativity, as cited in Ideas and Opinions (Crown Publishers, 1954), p. 376. Context: A concise encapsulation of relativity's relational core: physical properties emerge from interactions, not absolutes, echoing Mach's and Leibniz's critiques. Academic sources: Appears in multiple editions of Ideas and Opinions; often referenced in biographical works like Abraham Pais's Subtle is the Lord (1982). *4 - "Physics and Reality" (1936), reprinted in Journal of the Franklin Institute 221 (1936), p. 313; also in Ideas and Opinions (1954). Context: Einstein invokes Leibniz's concept to describe the relational harmony in physics, where laws emerge from empirical relations rather than absolutes. Academic sources: Full essay in journal archives; CPAE Vol. 6. @Xerxes

Thank you, @KJW . Your explanation helps clarify where our views diverge. You wrote: "Look around you. It is clear that we exist in a space that is at least four-dimensional. Even if we can't derive this space logically from first principles, we can assume its existence on the basis of empirical observation." I understand your point. And its seems reasonable at first. But that line of reasoning is structurally identical to early geocentric arguments: “Look around you - it is obvious that the Sun goes around the Earth.” Both rely on perceptual immediacy rather than logical derivation. The fact that perception appears spatial does not logically justify the postulate of a background. It only proves that our measurements project into four observable parameters - not that the universe is a 4-dimensional container. With WILL Relational Geometry (RG), I start from the opposite principle: Nothing is assumed. Everything is derived. The 4-parameter appearance emerges naturally from relational closure and symmetry - not from a pre-declared background. The crucial point is that both GR and RG reproduce identical empirical results: 1. Mercury precession [math]\Delta\varphi=\frac{2\pi Q_{\mathrm{orbit}}^{2}}{1-e^{2}}=5.0208724126 \times 10^{-7}[/math] 2. Gravitational Lensing [math]\alpha = 2\kappa^2 = \frac{4Gm_0}{bc^2}[/math] For light [math]\beta = 1[/math] implies [math]\\beta_Y = 0[/math] The orthogonal projection [math]\beta_Y =0 [/math] disappears; there is no dual axis available for symmetric partition. Therefore, the specific energy potential for light is not halved but complete explaining the factor of 2. 3. The radii [math]1.5R_s[/math] and [math]3R_s[/math] are known from General Relativity, their emergence here from two distinct and fundamental geometric symmetries[math]\theta_1=\theta_2[/math] and [math]Q=Q_t[/math] is not imposed but arises from the internal consistency of the WILL framework. 4. Time correction required for GPS synchronization [math]\Delta \tau_{{\rm GPS} \rightarrow {\rm Earth}} = \left(1-\frac{\tau_{Earth}}{\tau_{GPS}}\right)\cdot D_{ayS}\cdot M_{icro}= 38.5219216525~\mu\text{s/day}[/math] where [math]\tau = \kappa_{X}\cdot\beta_{Y}[/math] 5. Energy Symmetry law [math]\Delta E_{GPS \rightarrow Earth}+\Delta E_{Earth \rightarrow GPS} = -6.1265399845\times10^{-10} + 6.1265399845\times10^{-10} = 0[/math] and in the same time its not just conformation within RG: [math]\frac{U_{EGPS}+T_{EGPS}}{m_{GPS}c^{2}}= \Delta E_{Earth \rightarrow GPS} = 6.1265399845\times10^{-10}[/math] 6. And finally Galactic rotation curves [math]V_{\mathrm{WILL}}^2(r) = Q^2 c^2 = 3\beta^2 c^2 = 3 V_{\mathrm{bary}}^2(r)[/math] yielding the final law: [math]\boxed{V_{\mathrm{WILL}}(r) = \sqrt{3}\, V_{\mathrm{bary}}(r)}[/math] (with assumption of equilibrium state) tested on SPARC database 175 galaxies no adjustable parameters and fixed Y*=0.66 light/mass ratio for all galaxies yields RMSE=20.23 km/s *Happy to provide detailed derivations for any claim in this list. When two models give the same predictions, the principle of ontological parsimony demands preference for the one with fewer assumptions and free parameters. That’s exactly what happens here: 1. Mathematics becomes radically simpler (no metric, no connection fields). 2. Paradoxes and self-referential problems disappear. 3. Unique new predictions appear from relational closure alone. 4. Operational content increases - everything used is observable or derivable. 5. Physical meaning and intuition are restored - equations map directly to measurable relations, not to background abstractions. So I’m not disputing the usefulness of GR calculus; I’m showing that its predictive content can be derived from a cleaner relational base, where “space” and “energy” are two sides of the same invariant. And I find it hard to believe my self. It literally driving me crazy. And what I've showed its just a small fraction just a tip of the iceberg. Im not asking to believe me. Im asking to find the Truth together.

You know what I actually find arrogant? Unjustified declarations stated with full confidence - for example: "both your theory and category theory are deeply non-constructivist." Please pinpoint exactly where you see non-constructivism. Everything in my construction is derived step by step - see "Foundational Approach" above. Show the specific element that is assumed rather than derived. --- As for your second claim: 1. Let's assume, for the sake of argument, that I am tacitly using some metric. 2. Yet I can't find it in my mathematics. You can't find it in my mathematics. Nobody here has found it. It’s invisible. 3. It’s non-operational. It does not affect any outcome. The equations reproduce observation with high precision. 4. That makes such a "metric" a useless, non-operational artefact - pure ontological inflation. Would you call that fair reasoning? Or are you going to make another self-confident statement to prove my point again?

You ask if my parameter Q means I'm using a metric because it measures "how far" two centers are apart. No, there is no metric here. In GR a metric [ds² = g_{μν}dx^μdx^ν] is a background rule that defines distance inside a pre-existing space. In Relational Geometry, Q does not come from any background. Each observer places itself at (β,κ)=(0,0) and measures the other by its own relational projections. The closure [Q² = β² + κ²] is not a metric contraction but the relational difference between two observers. It looks like a distance, but it is a relational invariant, not a metric length. Please tell me what from this answer remains unclear for you?: I don't know. My best guess is no. But minimalization of assumptions to infetecimal is what Im trying to do. I got few questions for you: 1. Do you find my derivation of statement "Complex mathematics is the consequence of bad philosophy." rigours? 2. Do you find my "Relational Displacement as Q Parameter" operationally useful?

Did I miss your question? Last one you asked was this and I roll out the most detailed unswear so far: Completely agree. Due to forum format I cant just lay on you guys pages and pages of derivations so Im posting shorted versions and by doing so losing rigor and logical sequence. Maybe if Ill portion it in to digestible peace's?... Lets try and start from the top. This first part is mainly philosophy but we cant move forward without establishing foundations: This document must be read literally. All terms are defined within the relational framework of WILL RG. Any attempt to reinterpret them through conventional notions ... and so on... Was there another one that I missed? Thank you, Xerxes. No lectures here. Just using all I got. And yes, I took your hint seriously and tried to formalize the relation in categorical language. It turned out to fit remarkably well. At least it seems to me. I'm only starting to get familiar with category theory. In this scheme the "category of energy" is not the category of numbers but a symmetric monoidal posetal category that I call [math]\mathbf{Bud}[/math] – short for "projection budgets". Its objects are the dimensionless relational budgets [math](\beta^2,\kappa^2)[/math], and morphisms represent admissible transformations between them. The monoidal product [math]\boxtimes[/math] simply joins independent subsystems, and the unit object [math]e[/math] is the trivial (zero) budget. On the other side, the 2-category of observers [math]\mathbf{Obs}[/math] has: - objects – relational states (observers), - 1-morphisms – causal transitions labeled by [math](\beta,\kappa)[/math], - 2-morphisms – observer re-parametrizations (self-centering operations). From this we build the homotopy 1-category [math]\mathcal{W}=\mathrm{Ho}^1(\mathbf{Obs})[/math], carrying a monoidal product [math]\otimes[/math] for composition of processes. Then two strict monoidal functors arise naturally: [math]S,E:(\mathcal{W},\otimes)\to(\mathbf{Bud},\boxtimes)[/math] defined by [math]S(A)=\kappa_A^2,\quad E(A)=2\beta_A^2[/math]. Their natural isomorphism [math]\eta:S\Rightarrow E[/math] expresses the closure law [math]\kappa^2=2\beta^2[/math], which is just the WILL equivalence [math]\boxed{\textbf{SPACETIME} \equiv \textbf{ENERGY}}[/math]. So in this sense, energy and spacetime are functorially equivalent descriptions of one relational transformation, not distinct substances or metric entities. This is just my first attempt and its most likley wrong. But I hope it sufficient to see the idea in developing.