Everything posted by Genady
-
Negative times negative makes positive
I have assumed only that multiplication is distributive (on the step you have marked): (a-b)×c=a×c-b×c In the case above, a=1, b=2, c=-1.
-
Negative times negative makes positive
If we accept that -1 and +1 are additive inverses, and if we want to keep the distributive property of multiplication, then it appears that we don't have a choice but make (-1)×(-1)=+1. Here it goes: (-1)×(-1)=(1-2)×(-1)=1×(-1)-2×(-1)=(-1)-(-1)-(-1)=(-1)+(+1)+(+1)=+1 QED
-
Negative times negative makes positive
Regardless of being a root of +1, -1 is a label for the additive inverse of +1. How come we use the same label?
-
Textbook giveaway: Quantum Field Theory and the Standard Model by Matthew D. Schwartz
https://www.amazon.com/Quantum-Field-Theory-Standard-Model/dp/1107034736/?tag=pfamazon01-20
-
Textbook giveaway: MTW's Gravitation
https://www.amazon.com/Gravitation-Charles-W-Misner/dp/0691177791/?tag=pfamazon01-20
-
Negative times negative makes positive
I agree. For example, why i/-1 and not -i/-1?
-
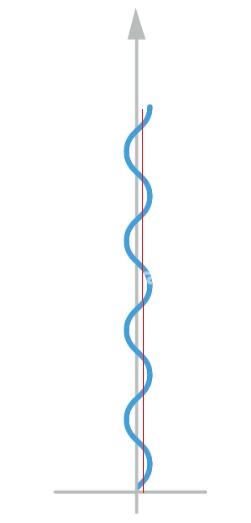
Geodesics.
Beyond the crash event, the geodesic will coincide with the worldline of the Sun (the red line).
-
Geodesics.
What is there to consider? What does make this scenario interesting or non-trivial? It is just a graph of \(x=x(t)\) function with \(x\) and \(t\) axes flipped.
-
Geodesics.
This will manifest in the shape of the wavy curve. It will be flatter farther from the Sun and steeper closer to it.
-
Geodesics.
The horizontal coordinate on the graph is projection of the asteroid position on the direction of the major axis. A geodesic is a line in spacetime, i.e., in four dimensions. To illustrate it in two dimensions, one needs to take a projection.
-
Geodesics.
On a scale of an asteroid orbit shown, the Sun is considered at rest relative to the orbit center.
-
Geodesics.
- Geodesics.
I think it is for a general ellipse, including circle. I don't see what makes it limited to circle.- Geodesics.
I think it is for an elliptical orbit.- Geodesics.
The horizontal axis here is some x, e.g., ellipse's major axis. The vertical axis is time. The wavy line is the orbit.- "Normal" Development with a Genetic Disorder
I understand that the OP question is about ontogeny of organism with a genetic disorder. What I don't understand is, what would make one to think that- Negative times negative makes positive
This is a good summary. +1- One of the most pointless phrases to learn in another language
Just like Russian! (I know it's OT.)- Negative times negative makes positive
Got it. +1- Negative times negative makes positive
I'd say that the basic operations are ascend/descend-by-one. Then to ascend/descend-by-two you just ascend/descend-by-one twice, to ascend/descend-by-three you ascend/descend-by-one three times, etc. To ascend/descend-by-zero you then ascend/descend-by-one zero times, i.e., you don't move. I think it is not difficult to swallow that to ascend/descend-by-(-1) you descend/ascend-by-one, to ascend/descend-by-(-2) you descend/ascend-by-two, etc.- Negative times negative makes positive
This is one of the recurring themes in this thread, e.g.,- Negative times negative makes positive
OK. We can use the "× -1" label to get from positives to negatives. How do we come to use the same label to get from negatives to positives?- Negative times negative makes positive
It is not so in the grown-up's algebra, but might be a good order for learning. However, there seems to be a logical gap there: To introduce negative numbers it uses multiplication by -1, but where does the -1 come from if there are no negative numbers yet?- Negative times negative makes positive
Ah, I see. IMO, adding and subtracting numbers do not reflect physical moving of objects but rather reflect ways of counting them.- Negative times negative makes positive
I don't understand. The example, 4-(-6), is neither a) nor b), I think. - Geodesics.
Important Information
We have placed cookies on your device to help make this website better. You can adjust your cookie settings, otherwise we'll assume you're okay to continue.