Rob McEachern

Not anymore. In twenty-first century physics, they have become accepted without ANY experimental evidence: "There is no more experimental evidence for some of the theories described in this book than there is for astrology, but we believe them because they are consistent with theories that have survived testing." Stephan Hawking, "The Universe in a Nutshell", Bantam Books, 2001, pp 103-104. “Sabine Hossenfelder argues, we have not seen a major breakthrough in the foundations of physics for more than four decades… The belief in beauty has become so dogmatic that it now conflicts with scientific objectivity… Worse, these "too good to not be true" theories are actually untestable…” https://www.amazon.com/Lost-Math-Beauty-Physics-Astray/dp/0465094252

It would be very interesting if it were actually true. But it is not. The most fundamental loophole of all, can never be closed, not even in principle; because strange correlations MUST exist, whenever two or more measurements are EVER even attempted on an entity, that only enables one (an entity that only manifests a single bit of information). For a more detailed explanation of this ultimate loophole, see http://vixra.org/pdf/1804.0123v1.pdf

Thermodynamics. That is where Fourier analysis originated. There is no wave function in any problem. The use of the term "wave" is a misnomer. The structure of Schrodinger's wave equation is unlike that of the classical wave equation. But it is identical to the classical heat equation; it would have been more appropriate to call it the Schrodinger heat equation, describing a process similar to heat-flow, rather than wave propagation.

Any experiment in which a multi-channel detector, responds to a mono-energy input (quanta) within each individual channel. That is what every Fourier transform's power spectrum describes. Thus, since wave-functions are mathematically described via Fourier transforms, it is true of every wave-function, whenever each "bin" in the transform receives only entities (quanta) with a single energy, Ephoton ,which may differ from one channel to the next. That is the origin of the Born rule. It happens with every experiment, that can be described mathematically via a Fourier transform's power spectrum (as are all wave-functions-squared), since it is a mathematical property of a Fourier transform, having nothing to do with physics. The only experimental condition that must be met, for the Born rule to be valid, is that each bin of the power-spectrum/histogram be obtained by a mono-chromatic integration of quanta. In other words Ephoton must be the same for all the photons detected in a bin, but can differ from bin-to-bin. For example, a diffraction grating or prism, will deflect photons of different energies/frequencies at different angles. Consequently, detectors placed at different angles will each receive photons within a single, narrow band of energies, thus ensuring the validity of the Born rule. On the other hand, if you remove the grating or prism, and let white-light hit the detectors, the mono-energy condition is not met and the Born rule does not apply - nor will you observe an "interference" pattern behind any slits, for that very reason. In the case of white light passing through slits, there is no longer a single, unique value for Ephoton , at each deflection angle, so the ratio Etot/Ephoton no longer yields a correct inference of N; you still get a spectrum (AKA interference pattern) but it no longer yields a correct inference of probability, or even looks anything like the more familiar interference patterns obtained with mono-chromatic inputs. “The important thing about electrons and protons is not what they are but how they behave, how they move. I can describe the situation by comparing it to the game of chess. In chess, we have various chessmen, kings, knights, pawns and so on. If you ask what a chessman is, the answer would be that it is a piece of wood, or a piece of ivory, or perhaps just a sign written on paper, or anything whatever. It does not matter. Each chessman has a characteristic way of moving and this is all that matters about it.” P.A.M. Dirac

Probability and energy density are related. Whenever the energy arrives within a detector, in equal quanta of energy, then the number of quanta detected by any given detector, can be inferred, from the ratio of total energy detected, divided by the energy per quanta. This fact is independent of the nature of the quanta; the debate about particle vs. wave is irrelevant. All that matters is that the quanta have equal energy. Which is why the experiments are always designed to ensure that is the case.

Ideal rambling. Prove my demonstration is void.

I already have. See below. By the way I am not so young anymore either; Been there, done that. No ramblings are involved. I previously provided links to both a "much better defined", line-by-line computer demonstration, together with a paper that describes it, that falsifies Bell's claim and all the existing claims for "loop-hole free" Bell tests (by actually constructing classical entities, that falsify the most fundamental, unrecognized assumption of all, namely that there is "something else to measure" after the first measurement has been completed). Anyone can reproduce the result on their own computer. It has been publicly available for two years, been reproduced by others, and no one of the over 1000 different people that have downloaded the demonstration to date, has been willing to publicly declare that they have found any error it. When I challenged some of the usual suspects here to attempt to do so, they all went silent - see the last post in the thread "Is there any reason this Quantum Telegraph couldn’t work?"; they would rather shut up than calculate, when it means their dogma is being falsified. That is one of the major problems with physics today, everyone says "put or or shut up" and then, when someone actually does "put up", very few are willing to ever admit that they cannot find a flaw in the argument; for fear of "losing face" if someone smarter than they, eventually comes along and finds the flaw, making them look dumb. So everyone just sits on the fence, hoping someone smarter themselves will come along and save them and their dogma. If you think you are that person, then hit me with with best shot. But don't give me any more "ramblings on the fringe of Science": State exactly were some problem lies within the computer demonstration, after you have downloaded it and run it, and actually thought about what you are witnessing. Put up or shut up. I'm calling your bluff.

On Challenging Science, particularly Physics, You have my sympathy Reg. Most living, theoretical physicists have yet to recognize (even though the long-dead masters, like Einstein and Schrodinger, repeatedly warned them about it) that they have fallen victim to the very problem noted in studiot's quote. Fools rush in, where wiser men have feared to tread. When you attempt to "measure something else", that your theory suggests exists, but that does not in fact actually exist in nature, then your theory "offers little" (though a little may nevertheless be a lot better than nothing). As I have pointed out in other threads on this site (to the dismay of the usual suspects), the uncertainty principle, the EPR paradox, Bell's theorem and all related matters are based on the supposed "self-evidently true" assumption, that after you have made a first measurement (as of position, or spin in one direction), then the ability to "measure something else" (like momentum, or spin in a different direction) should always be possible. But it is not always possible. In fact, it is impossible by definition, whenever the thing the physicists are attempting to measure, happens to manifest only a single bit of information. In that peculiar event, there is nothing "else" present, that can ever be reliably measured, not even in principle. That is what is meant by the term "bit of information" in Shannon's Information Theory. In this peculiar case, all measurements, after the first, must either reproduce the first, or be nothing more than an erroneous measurement of the first - by definition. Thus we now have quantum vacuum fluctuations, virtual particles, qbits, spooky action at a distance, etc. etc. ... all to account for those errors as being "something else", other that what they actually appear to be, producing weird correlations, that are consistently misinterpreted on the basis of the false assumption; namely that they "measure something else", something other than the ultimate “elementary particle” in reductionism, the least-complex possible entity, an entity manifesting the least-possible number of bits of information - a single bit - offering no possibility whatsoever of any uncorrelated, second measurement. Quantum theory is infested with such bad interpretations - assumptions about "measure something else", like blaming particles/waves/wavefunctions passing though a pair of slits for a supposed interference pattern, rather that recognizing that the pattern is merely the Fourier transform of the slit's geometry (more specifically, its power spectrum), and has little (but not nothing) to do with anything, particle or wave, passing through the slits. It's rather like blaming the light from the sun, for the visible pattern of your mother's face - How did the sun know what my mother's face looks like?!! Surely it must, for how else could I ever observe the pattern of my mother's face, if the sun was not emitting light that already knows/contains that pattern, before it ever struck her face?!!! But as Dogbert-the-physicist might say, "My theory is totally, totally different! My light, shining through the slits, really does know everyone's face, even before they were born! It all has to do with BlockTime! It has nothing to do with faces or slits modulating their information content, onto a carrier, that is, by itself, almost entirely devoid of any information!" Again, you have my sympathy, Reg. But you can take some solace from Stephen Hawking's quotes (The Universe in a Nutshell) "There is no more experimental evidence for some of the theories described in this book than there is for astrology..." and "Einstein thought that this (the EPR paradox) proved that quantum theory was ridiculous: the other particle might be at the other side of the galaxy by now, yet one would instantaneously know which way it was spinning. However, most other scientists agree that it was Einstein who was confused." And therein lies the difference between the wise men of old, that urged caution about such interpretations (a message not lost on their students, who subsequently urged their own students to “Shut up and Calculate!”), and all the later-day fools (Hawking's "most other scientists" AKA physicists) that rushed in, and ignorantly assumed that they, unlike their elders, could not possibly be confused by experiments that might "measure something else", other than what their new dogma proclaimed that they must have succeeded in measuring. So, as you have attempted to point-out, sometimes a difference between theoretical predictions of planetary motions and observations, can be correctly attributed to the prevailing wisdom/dogma of the day, such as an undiscovered planet. But other times, it "measures something else", like a previously unguessed, relativistic effect. But nowadays, as Hawking's quote indicates, more and more theoretical physicists have come to actually believe that the "beauty of math" alone justifies all their beliefs, in their favorite conclusions, deduced from their favorite "self evident" assumptions, and experimental evidence is neither necessary nor desired, to sustain their beliefs, anymore than for those believing in the "beauty of god." Because, “Hey, my conclusion really does follow from my premise! So it must be valid!” The possibility that the math just might, with absolute perfection "describe something else", a different premise, other than what the prevailing wisdom/dogma has supposed (the possibility suggested by the older generation of acclaimed physicists, like Einstein), has been summarily dismissed, as an "unnecessary hypothesis", by the lesser-lights in today's constellation of "best-selling" physicists. Laplace would roll over in his grave. And Santayana did say that "Those who cannot remember the past are condemned to repeat it." And Bacon would say "I told you so - 400 years ago - premises can only be justified via inductive reasoning based on actual observations, not deductive logic, however clever." Perhaps, since few physicists seem to (correctly) remember the past, I should note that Bacon decried Aristotle's over-reliance on deductive reasoning, for delaying progress in science, for 2000 years, since he thereby convinced philosophers to value deductive logic (inevitably based on unverified premises) above any actual observations of the real world, that might actually reveal that some premises probably (but not certainly) ought to be preferred over others. And now, for the past half-century, history repeats itself, and most present-day physicists see nothing at all of value in what the old philosophers had to say about such things, or even what older physicists of Einstein's caliber had to say - they were all just "confused", to use Hawking's term. As the old saying goes, the race does not always go to the swift and the strong, but that is the way to bet. I’m betting on Einstein’s conception of the universe, not Brian Green’s, or Stephen Hawking’s, however elegant they may be. Dubious premises result in dubious conclusions, regardless of their beauty.

Feeling the need to eat and feeling hungry are two very different things, for those dealing with frequent low blood glucose levels. It is not low blood sugar that makes you feel hungry. For example, a type-1 diabetic may feel absolutely bloated and stuffed after finishing a large meal, but still have a dangerously low (and still plummeting) blood glucose level, as the result of a fast-acting insulin injection, which may enter the system, before almost any of the previously consumed food has. Pure glucose gels and tablets, when eaten, enter the blood stream much faster than other carbohydrates, like pasta, and more than an order of magnitude faster than fat and protein. So the answer to your question is all about the timing. When your body really needs glucose, it needs it now - not an hour from now, much less a day from now. It is rather like needing air; it does not matter if you can be supplied with all the air in the world, a few minutes after your heart and/or brain have been permanently damaged due to an earlier short-term lack. A type-1 diabetic can lose consciousness in a matter of minutes, once their blood sugar starts to plummet, even when their stomach is full. The problem is, it is full of food, including most types of carbohydrates, that are absorbed more slowly than a fast-acting insulin. Consequently, it is not just the quantities of carbohydrates and insulin that matter, in this type of situation, but their respective absorption rates. That is why a very rapidly absorbed carbohydrate, like pure glucose, may need to be consumed, in spite of a full stomach. Once a diabetic has become unconscious, and thus unable to consume anything, the situation may be quickly reversed by either injecting glucose directly into their bloodstream, or as is usually preferred, by giving them an injection of the hormone glucagon, which causes the liver to rapidly (in a matter of minutes) release glucose into the bloodstream. An over-weight person is likely to have type-2 diabetes. They too will have problematic swings in their blood-glucose levels, just not as extreme as those likely to be encountered by the rarer type-1. But in either case, hunger and low blood glucose levels are not the same thing; one may feel the need to "eat something", in response to symptoms other than hunger, that tend to become familiar to diabetics, that have to deal with these other symptoms, on a fairly regular basis.

It should be even more obvious, that if you change V, V will no longer be constant, as stipulated in the text book quotes, as the defining property of a free particle.

Yes it is. E= (Kinetic energy + Potential energy) = (K+V). So (E - V) = K+V-V = K; the potential exactly cancels out in the special case, where V is a constant, regardless of what the value of the constant is. Note also that, given the expression for p, p2/2m = (E-V) = K = mv2/2, just as one would expect, for a free particle with only kinetic energy. The momentum cannot change if the particle is free.

Of course - because the potential has no effect, thus, the particle is free. Here is a quote from Merzbacher, "Quantum Mechanics", second edition, pages 80-81: .

It is not possible. The solution that you gave and claimed; "Which I think is more useful as you can plug numbers into it." Is not a solution to Schrödinger's equation, if the energy changes. You will find the same thing in any other text book on the subject. The author of the text cited, was David Bohm - a rather highly regarded figure, in quantum theory.

In the book, there is a two-step process to evaluate a square potential: (1) solve the equation when the potential is constant everywhere (Swansont's question), which is done in the first paragraph, and then (2) evaluate what happens when a second level is introduced. But, if there is no second level (as in the question that was asked), then all the rest of the book, after the first paragraph is irrelevant: There is no second level that is less than the first. Potential wells exist when there is a relative change in potential. The partial derivative of kx with respect to x, depends upon both the derivative of k and the derivative of x, with respect to x. The derivation of your solution assumed the derivative of k with respect to x is identically zero - there is no dependency on position. It also assumed that the derivative with respect to time is also identically zero - there is no dependency on time. Hence, k is being assumed to be a constant, right from the start; it depends on neither of the two variables (position and time) in the equation. I fail to see why you find that to be an interesting result; all it says is that a static sine-wave exists. How does that revelation enlighten your knowledge of reality?

There can be no well, if the potential is constant everywhere; wells require more than one level of potential. Where there is a well, there can be no free particle. Nothing can change in the solution you gave, because, in the derivation of that solution, "k" was unwittingly assumed to be independent of both time and position.

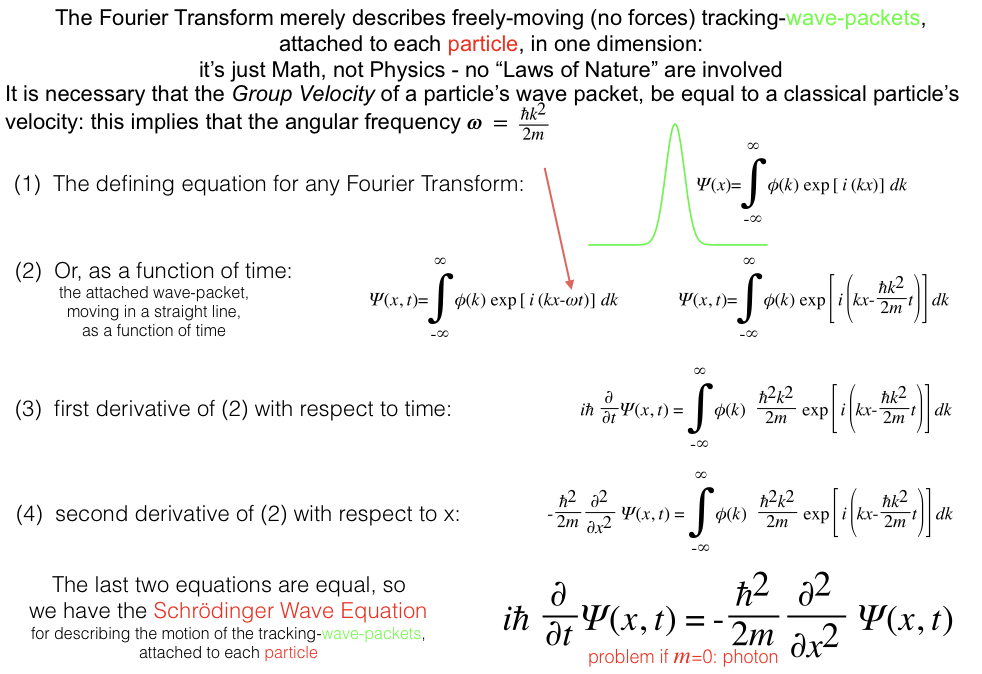
It does not change in your solution. That solution was derived by assuming the potential is zero, and E is a constant. You can find a simple derivation of that solution, in the last answer given on this page: https://physics.stackexchange.com/questions/347996/when-solving-the-schrodinger-equation-how-do-we-know-what-functions-to-use-exp Just set the potential V0 = 0 and solve for "k". But note that now, you have left out the "x" in the solution. It should also be pointed out, that the very first step in this "derivation", assumed that the derivative of "k" with respect to x is zero. Think about the consequences of that assumption. Everything. Because it demonstrates that Schrödinger's equation is just the expression for the Fourier transform of a wave function, transformed into a differential equation. Consequently, all the properties associated with wave functions (such as the uncertainty principle, superposition, entanglement, vacuum fluctuations, the Born rule etc.), turn out to be purely mathematical properties of Fourier transforms and have nothing to do with physics per se. In other words, these properties are properties of the mathematical language being used to describe physical phenomenon - not properties of the phenomenon being described. Consequently, attempting to interpret any of these properties as a physical phenomenon, rather than as mere side-effects of a specific mathematical technique (Fourier transforms) being employed, is a pitfall, that has confused the physics community for 90 years. See: https://books.google.com/books?id=hEHCAgAAQBAJ&pg=PA232&lpg=PA232&dq="In+any+region+where+V+is+constant,+the+solution+of+the+wave+equation+is"&source=bl&ots=n0Kf89ulEE&sig=b-_mFvKHojT3NTPKOew-0CugX-g&hl=en&sa=X&ved=0ahUKEwiG2cTrvdnaAhWjrVkKHTgiCDoQ6AEIKjAA#v=onepage&q="In any region where V is constant%2C the solution of the wave equation is"&f=false

You stated you were only concerned with solutions "for a single particle translating freely in space": a potential, that has any effect whatsoever on a particle, implies that the particle is not free. is not even a function of time, so it does not represent anything "translating" anywhere.

Equation (2) is the general solution!

You have reversed both cause-and-effect and history. Schrödinger derived his equation, for a free particle, from the a priori known Fourier Transform of the wave-packet that he (following de Broglie) "associated" with a particle, as a sort of tracking mechanism. The derivation of the Schrödinger equation for a free particle, consists of little more than computing the first partial derivative of the Fourier transform with respect to time, then the second partial derivative with respect to position, and then equating the two.

Exactly my point. Superpositions only exist as a mathematical abstraction, and abstractions do not collapse. So was the entire physics community. Schrodinger set out to develop a physical model of the trajectory of a particle, by using Fourier transform based superpositions, to describe a wavepacket, that "accompanies" a particle as it moves. But he eventually realized that while his equation provided a good computational model, for producing results, it resulted in an absurd physical model. Thus, he introduced his cat, in an attempt to convince people that one should never attempt to "interpret" a wavefunction as anything other than a useful computational device, which has no known relevance to a physical model, such as an actual propagating wave. In the case of the coin, as in the case for spin and polarization, the state being observed, is not a property of the entity being observed. It is a property of how the observer decides to observe it - the observer will obtain different results, if the entity is observed from different "directions". In other words, "calling" an entity "spin up" or "heads" is not a statement about the state of the entity. It is merely a statement about what the observer happens to "measure" when observing the entity from a particular direction.

Yes. A coin is in a superposition of being both "heads" and "tails". Always. Even after you "call it" one or the other.

I never said it was. I said "imply the existence of a force". Do you really wish to maintain the a gravitational potential does not imply the existence of a gravitational force, and that that in turn implies that objects at different heights from the center of gravity would experience different accelerations, if not preventing from falling by some other force?

However, interpretations do have a significant impact on where, or even if, one looks for answers. For example, last summer, I posted a link to a detailed demonstration, on this website, falsifying the supposed "loop-hole-free" verification experiments of Bell's inequality theorem. That was motivated by a different interpretation. I have noticed that the two of you, in particular (and many hundreds of others) have been noticeably silent about all the errors you have found in that demonstration (and before you ask, yes, the results have been replicated by others). Physicists like to disparage the "god of the gaps", all the while talking about wave-functions and super-positions, as if the "wave-function of the gaps" is more real than the "god of the gaps". But wave-functions and superpositions are no more necessary to explain observations than god is. And the continued belief in all such things has hampered scientific progress. That is the difference interpretations make; bad ones, based on unobserved gods, superpositions and wave-functions, induce dogma, which in turn stifles progress. So let me put this to you. Above I just told you why quantum theory is entirely probabilistic - not because reality is, but because quantum theory amounts to nothing more than a very complicated procedure for constructing histograms, in an attempt to describe that reality. That is not what was intended by its developers. But it is what they inadvertently developed, for better or worse. So why not take that new-found insight and try to develop a theory, that is not based on histogram-inducing, Fourier superpositions. Communications engineers (the inventors of information theory) did this a long time ago and it resulted in a revolution in communications technology. Maybe it is time the physics community gives it a try too, rather than "shutting up and calculating" the same old histograms over and over again and wondering why so little progress is being made, in fundamental physics.

No. You made an incorrect interpretation of my comment. You seem to have interpreted my use of the word "acceleration" as implying only to a change in velocity (or speed?), rather the the more inclusive use of the term to imply the existence of a force (such as a gravitational potential). You seem to have assumed that I believed that the effect is solely due to relative motion. But I said no such thing.

Obviously. Please read what I said. My original comment stated that the space-traveler experiences 1g, total, not 1g from gravity plus 1g from thrust or anything else. The whole point is to arrange for the traveler to experience the EXACT same experience as the non-traveler. That cannot be done unless the thrust is continually adjusted to compensate for the change in the gravitational potential, due to increasing distance from the earth.