Tom Booth

Could you please define/translate/explain that. I'm not familiar with that acronym or whatever, text slang? And find nothing in a search that clarifies it for me.

Alternative wordings/synonyms such as "disappears", "no longer exists", "vanishes", etc. may be substituted in place of "destroyed" (Carnot Reflections, Appendix A). When "heat" (as a form of energy transfer) goes out of a working fluid as thermodynamic "work", my understanding is that the working fluid undergoes a drop in temperature as a result. In other words, a change in the total energy of the gas (working fluid or air, in a hot air engine) is measurable as a change in temperature. If the energy supplied to the engine in the form of heat goes out of the engine in a different form (mechanical motion of the piston, flywheel, etc.) Then the energy that formerly existed in the form of sensible heat, detectable with a thermometer, no longer exists within the working fluid as such, or in any other form whatsoever, latent or otherwise. In a manner of speaking then, the "heat" has been "destroyed" utterly, as far as the energy accounting within the working fluid is concerned. That energy that has been transformed into mechanical motion must be deducted from the working fluid. This manifests as a drop in temperature. Is this not a correct viewpoint as far as mainstream science is concerned? A natural consequence of the first law of thermodynamics (conservation of energy).?

As I do not wish to ignore replies and comments, quite the contrary, I will attempt to follow up, and or address any additional replies and comments here, if that's OK. Or you (someone?) tell me where my making a response to replies and comments is allowed. It appears to me it is when I DO respond with evidence in support of my observations, theories or statements etc. That my threads are abruptly shut down.

My thread on Maxwell's Demon was closed, presumably for the reason cited: I was however, completely unaware that there could be any argument about this point, had never been challenged on, or given any opportunity to support this well known and scientifically established fact. Therefore, if I may, I shall do so here in the Lounge where allegedly we are free to discuss "anything". First citation [emphasis added]: A further citation [emphasis added] Additional citations to follow as my time will allow.

If that were the case, anyone could take the air conditioner out of their window apply some heat to it and turn it into an electric generator.

IMO, and I've studied both heat pumps and heat engines for a very long time, your comment only demonstrates a lack of understanding regarding the details of how either machine or appliance actually operates. These "Ideal" scenarios of a heat pump actually being a heat engine running backwards are about as silly as saying: if you turn the crankshaft on your lawnmower backwards it will produce gasoline. A heat pump running backwards is an air conditioner. All either one does is move heat one way or the other. A heat engine consumes heat. Creating cold by moving heat out of an insulated space is not the same as creating cold by converting that same heat into mechanical work output . In a heat engine the heat does not disappear at the evaporator and reappear at the condenser. It just disappears. Period. Consumed as "fuel" to produce a mechanical motion. The cold produced by a heat engine is not the result of simply moving the heat through the engine from one side to the other, taking it in at the heat source and transporting it over to the sink. The cold produced by a heat engine is the result of destroying the heat, so that it no longer exists. You can't push your car backwards to fill up your gas tank.

That's quite a mouthful (again) [emphasis added] Interesting how changing the name of an appliance changes the rules regarding how we are allowed to think about it. A "refrigerating effect" from a Heat engine is dismissed offhand, but a "refrigerating effect" from an apparently identical appliance based on the same known physical principles is not only accepted but vigorously defended with mathematical proofs. An example of how past assumptions can blind the mind to reason and the eyes to objective observation. Whenever has "mainstream science" not sooner or later been overturned, reframed, or reinterpreted?

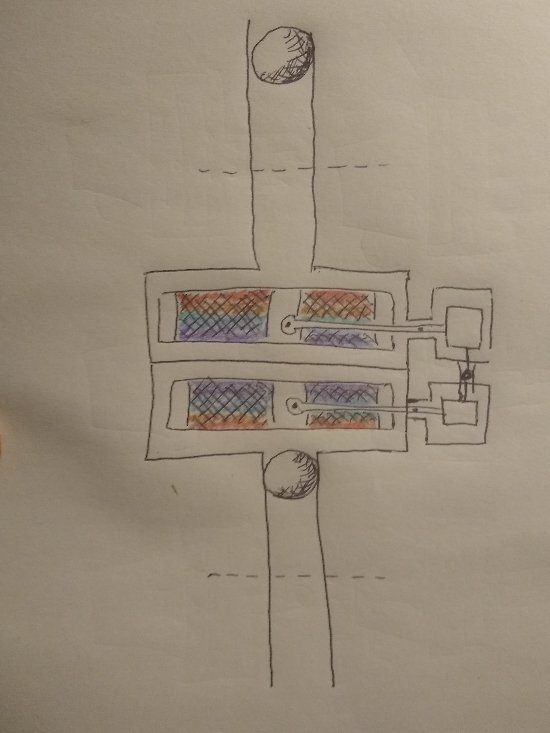
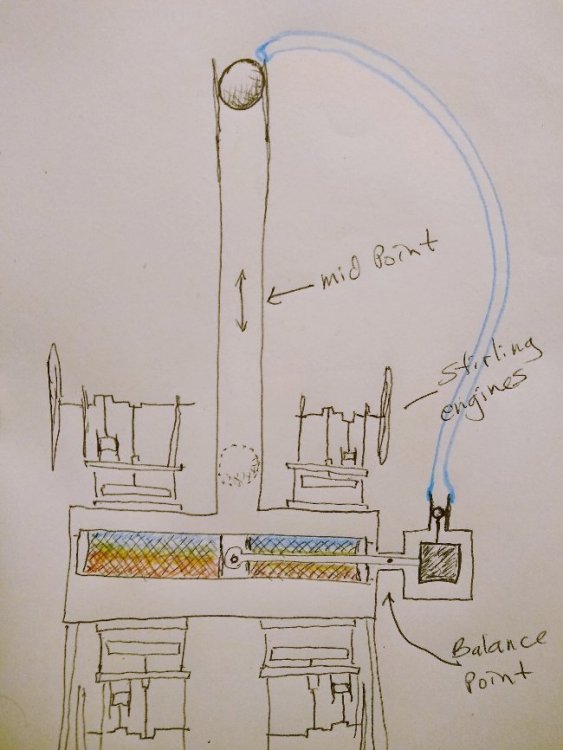
As far as, well, a couple of things, like is this "PM machine of the 3rd kind" [sic (?)] Actually "one-off" or, what happens after a ∆T is established and heat starts immediately migrating across the system boundaries. The device is, after all, not "isolated" from the environment. Maybe Ghideon can help me out again with this one. Now the ambient heat might have a really difficult time trying to find its way in between the two ah... Ruchardt tube thingamabobs. Dropping the ball to get the thing(s) off and running is pretty much the equivalent of giving the flywheel(s) on a couple of LTD Stirling engines a quick spin. Anybody know where I can get an upside down Ruchardt apparatus? Not really sure if I drew that properly. It's just a concept drawing.Too early in the morning to think about all the details. Anyway, maybe it might be possible to prevent the surrounding ambient heat from immediately destroying the slight refrigerating effect using the Ghideon method.

Actually the "Maxwell's Demon" contraption is more like a Gamma Stirling (Dr. Senft's P-19) except for having a "free piston". With a little heat on the bottom to make up for friction loses, I was thinking too, what if we put a coil around the tube like one of those "forever" flashlights you shake to light, or charge. One disassembled: I guess a little more heat would be required to compensate for the linear generator output. Oh wait, I forgot, this engine, I mean Ruchardt tube thing doesn't have any friction loses. Well not much anyway. So it's just the generator output we'd have to make up for? No, wait I forgot, we'd have to multiply that by like six times. I just have to remember to always call it a *Ruchardt tube generator* and not a heat engine. Because if I call it a heat engine that would automatically drop the efficiency down to practically nothin'.

I was thinking that given the "fact" (if true) that a Ruchardt apparatus and a Stirling engine, (with no load, of the "thermoacoustic" type, operating without a flywheel) are essentially very similar, if not identical, then perhaps applying some heat to the base of the Ruchardt bottle would make up for frictional loses and keep the thing going, as long as some heat we're continually applied. Any thoughts on that arrangement?

I spent some time reading up on what you mention here: "So it's also a candidate for perpetual motion machine of the third kind." The definition of this "third kind", as far as I can find, relates only to the device being frictionless. A frictionless mechanism or machine that is also a "simple refrigerator"? You don't think that runs a bit further off the rails than just a run of the mill impossible, let's say, a top spinning in zero gravity but not actually doing anything. You don't actually BELIEVE this thing could just bob up and down, perhaps for weeks or months on end, effecting the simultaneous refrigeration AND heating of a finite space all the while, do you? Because I don't. You would need to do more convincing than just saying "dU + dEP = 0 is not a really hard sum to solve." Suppose we fashion a small compartment or two. Insulated? I'm supposing. Do you imagine this machine could keep an ice cube cold? That is, the machine is already effecting refrigeration, let's just suppose, maintaining a cold side at <or=0°C. Putting an already frozen ice cube in the compartment would not upset the balance of the machine would it?

Right, I agree, but I'm having a little difficulty pinpointing what that "energy input" is exactly, which involves looking at the details. I'm well aware of the broad assumptions, 2nd Law "It's impossible" etc. Frankly I'm rather shocked with the response from sethoflagos. He considers it nothing more than a simple refrigerator, that runs by itself, forever (?) And seems to have worked it out mathematically with great confidence. Yup, just your ordinary household appliance. Nothing to see here folks. BTW, I cannot really say that this device is my own invention. It came to mind after watching many videos and such about the Ruchardt Experiment and noticing how much this apparatus resembles a Stirling engine. What this is, basically, is just a Ruchardt apparatus with a Stirling engine type regenerative displacer put inside, or alternatively, it IS simply a common "free piston" Stirling engine in toto.

sethoflagos has alleged that my proposed Maxwell's demon could work, in principle, indefinitely. I'm just trying to do an energy audit. Your rant does not address the question of where exactly the startup energy came from. I'm not saying there was not any necessarily. I, though, did not directly supply any heating element or electrical input. Suppose the system is set up with the ball/piston on a platform. Remove the platform to start the machine. What if there is the machine running and say, the top of the cylinder is slightly elastic. I push a button causing it to be squeezed. So the ball/piston gets stuck. Now push a button to re-release the ball, the system has STARTED up again from a standstill. Do we use, what is it, mass x distance. f=m*a ? Or what? Newtons second law of motion? Is that MY energy input? Gravitational force?

Good grief, I'm not doing any such thing! Infact I offered one possibility. I lifted the ball/piston, putting "potential energy" INTO the magnetic piston before dropping it down the tube. You do understand, this idea for a "Maxwell's Demon" contraption only just popped into my head about 20 minutes before I started the thread. Why this confrontational attitude all the time? Heckling, put downs, insults, mischaracterizations, It's like I'm some road kill being picked apart by a flock of vultures. Basically I'm just thinking out loud, asking myself, as much as the forum. I'm not denying there needs to be a source of energy to set the thing in motion, initially at least, and I would assume energy would need to be supplied continuously as well, if it were to continue operating more than a few seconds, even with friction reduced as much as possible. That's my honest opinion. I'm also not talking about any "ideal" or isolated system. There is no insulation on this thing, though glass is a fairly good insulator, it's not perfect. So if there is a hot and cold side being maintained for any length of time, heat will begin to migrate in and out of the system. Anyway, one step at a time. What specifically is the actual impetus that gets this thing started? I'm just honestly asking for a little help reasoning this out. Did "l" Tom Booth, literally PUT energy into the "system" in some way? If so, do you agree with my first analysis, that it was lifting the magnet that put energy into it? What if I took the magnet down from a height. Let's say I hiked up to the top of mount Everest and found it there at an elevation of 30,000' (almost) then carried it down to my house on the seaside, dropping it down the tube. I guess then the energy was put into "the system" when the mountain was formed? Is it possible, if instead, I carried the apparatus itself up the mountain, could I then put much much more energy into the system, so I don't loose all that energy put into the piston eons ago when it was lifted up by the mountain? Carrying the piston down from the mountain, no doubt caused a great deal of loss in potential energy, I would think. How do we quantify the initial energy input, I guess, is what I'm asking. How would that be determined?

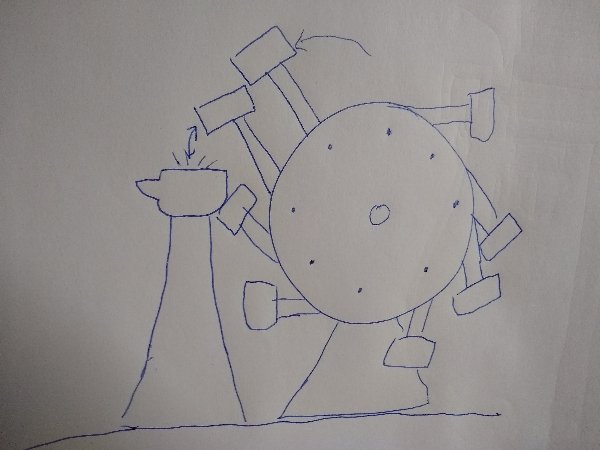
Just to be clear, what do you consider "that little initial energy input"? We lifted up the magnet giving it potential energy, then dropping it released the energy. I'm a little skeptical that there could be any heat pump effect from that. The weight drops down the tube compressing the air, the little piston goes up, the regenerator goes down sweeping up some heat (since the compressed air heated up immediately but the regenerator did not), so heat moves from the compressed gas into the regenerator. I'm afraid at that point the bounce has already been taken out of the air. Like your on a trampoline and suddenly it collapses. Or does the piston just fall a little further maybe and still bounce? If it falls a little further does it also increase in velocity a little? Does that increase or decrease the potential energy, by cooling the gas with the regenerator. If we imagine we do still get a bounce that expands and cools the air, the regenerator falls and releases the heat it previously gathered. Could that release of heat cause the piston to travel up the tube a little further? If any of this actually worked at all, and a temperature difference we're established and could be maintained. There would then, presumably be heat transfer into the device on the cold side and transfer out on the hot side. The regenerator is preventing a heat transfer in the other direction. Anyway you didn't address the possibility of a heat engine on both the top and the bottom to balance the energy exchange. Anyway I'm pretty satisfied that it might be an interesting project to build the thing just to see what happens. Thanks. I might try building that Hammer wheel as well. With an anvil. I have an idea it could work with a foot peddle. I'm wondering if it was not actually a misunderstanding that it was intended as a perpetual motion thing. Maybe the author/inventor (if he was the inventor) meant simply that this was a SELF running hammer wheel in the sense that a blacksmith could run the thing by himself, rather than have to hire extra people working in shifts to perform the hammering, to put a metal roof on a cathedral of something.

That seems overly generous. Personally I wouldn't expect the effect to carry on for more than perhaps ten seconds. I find the term "closed system" a bit perplexing sometimes. Take a heat pump or air conditioner. Would that be a "closed system"? Depends on what you imagine the "system" to consist of doesn't it? For example, there are, in an air conditioner cooling coils, cooling fins and a fan blowing air through a radiator. The heat exchanger has matter passing through it. No more incoming heat? The heat of the atmosphere did not run out. The Stirling engine is converting some of the heat into work, so there is, if anything less heat transfer into the system than before. But supposing heat entering into the "Demon" contraption on the cold side, through the Stirling engine is actually a problem, could the excess heat be carried off by a second engine underneath the apparatus on the hot side? The one engine on top on the cold side adding heat, the other on the hot side taking an equivalent amount away. Maintaining the balance? At any rate, haven't we already gone too far, I mean, Maxwell's Demon is supposed to be impossible, not on the basis of heat added or removed from the system, but on the basis that the demon has to think and so uses energy in the process of opening and closing the hatch in the partition.? Here we have a purely mechanical contrivance, so no thinking process to consume energy. I'm probably not relating the argument correctly, but I don't recall anything about adding or taking away heat being an issue. The separating out of the heat in the first place is what's supposed to be impossible, as I understand the problem. I can't follow this at all. Could you rephrase or clarify that?

If we simply rule out possibilities on the basis of: "It's never been done before" and little else, I think we may be repeating a long train of mistakes. Making broad assumptions rather than relying on the scientific method.

Thank you for that, at least. OK, I can go along with that in principle, basically. So are you suggesting that if we leave off the Stirling engines, this could be some kind of PM machine? Just that it could not put out any outside work, or what exactly? At what point would the system break down by placing say, one Stirling engine on the cold side. Ambient heat would then run the Stirling engine which would then drop it's "waste heat" into the device, which the Maxwell's Demon could then set about separating out.

This is better. Can you elaborate? Has something like mass, or any other physical property been neglected? What did I overlook? But no, we are not intentionally postulating an "ideal' machine, without mass, or friction if that's what you mean. The emphasis should be on the word "Real". Idealizations, machines with zero mass and so forth are not "real". How do you know that? Not being familiar with it, this Honnecourt device, I just took a look at it. Honnecourt apparently never referred to this machine as a "Perpetuum Mobile". Rather he called it a self-moving Hammer wheel, or something to that effect. His notebook is otherwise full of down to earth, very practical building techniques and so forth. To me, this Hammer wheel looks like simply a labor saving device employed perhaps, for hammering metals, copper plate, Iron, that sort of thing. Such a device would be used in conjunction with an anvil. As I've crudely illustrated here: Does that perhaps change the dynamics of the machine? Have you ever worked as a blacksmith? What happens when a hammer strikes an anvil? For every action there is an equal but opposite reaction. So under actual use, in real circumstances, the hammers would bounce back up from the anvil, perhaps maintaining the "overbalance". Is that possible? Should my hypothesis be tested? At any rate, an ingenious labor saving device even if it requires an assistant to turn a crank, the weight of the hammers is balanced. Saves someone the work of continually lifting these massive weights to pound wrought iron. A very practical blacksmiths tool and nothing more. Or could it actually be "self turning"? Whoever tested it under real world conditions. Actual use?

To me "Awareness about the limits of physics" reads "preconceptions about...." "...focusing efforts on what is (assumed to be) possible and rejecting the (presumed to be ) impossible ideas early (or prematurely). With an arrogant attitude, presuming we already know everything there is to know about the universe, there would never be any further progress in human understanding. That's quite a mouthful Having, I think, fully described the theory and mechanics of the proposed device itself, what aspect of the theory and operation is contrary to established science? Established when, by whom, using what empirical methodology and based on what experimental data. I seem to be about the only one to have actually read through the rules of this "speculations" forum making some effort to adhere to the guidelines. Are we to accept 17th century scientific "Law" based solely on the grandfather clause?

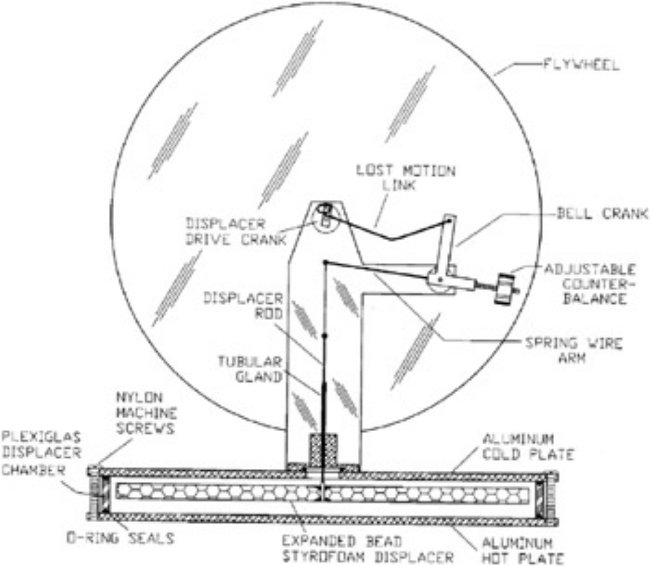
The movable regenerative heat exchanger in the P-19 was incorporated into the styrofoam displacer, in this manner: The air passages cut out of the styrofoam were filled with the regenerator material consisting of a light weight metal mesh. Regenerative displacers of this type are fairly common with "Ultra low temperature difference" type Stirling engines nowadays. The Vuilleumier heat driven heat pump also incorporated such regenerative displacers. As expressed by the Wikipedia article on the subject: I don't think in terms of "Laws of Physics" generally. In modern scientific method theories are postulated and subject to empirical verification and are experimentally validated or not. In that spirit, this is not any discussion about any "Laws" new or old. Just a theory about how a potentially real Maxwell's Demon might operate. A regenerative displacer in a Stirling engine, or in a Vuilleumier machine behave in a manner that IMO very much resembles a Maxwell's Demon, effectively marshaling the heat to one side of an air filled chamber. Virtually no work is involved in accomplishing that. It is just a matter of allowing the heat to do what it does and move into a colder object or material. During compression the temperature of the air is elevated above that of the regenerator, so the heat transfers to the colder regenerative material. During expansion, the air cools and therefore the heat moves back out of the now relatively hot regenerator and back to the cooler air. The counterbalanced regenerative displacer is virtually or effectively weightless and only needs to be moved back and forth, or up and down a small distance in order to effect a movement of heat from one location to another location where it is then deposited. Such a process does not require any overthrow of any well established and experimentally verified "Laws of Physics" that I'm aware of.

What about it? The Maxwell's demon (this one anyway) does not generate any energy or heat, it just sweeps up the already existing heat. The area from where the heat was swept up, of course, is left cold. This is akin to gathering firewood. Naturally, though, if heat is taken away from some area, more heat will tend to move in to take it's place, then that can be swept up as well. A similar counterbalance was utilized in the P-19 Low Temperature differential engine described by James Sent, which ran for two weeks on the temperature differential produced by a wet sponge (evaporative cooling): The idea being that the regenerative displacer, being perfectly counterbalanced by a weight requires virtually no energy to move up and down and yet serves to reclaim potential waste heat. The efficiency of such recuperative heat exchangers is reportedly as high as 95%

Nothing related to the function of the Maxwell's Demon itself. But if a temperature difference can be maintained, that would be something that could be done with the ∆T. Run a thermal differential engine or two, or three, or four or eight or whatever. The action of the pivot arm, counterbalance, actuated by changes in pressure is similar to this compressor driven heat pump, except that the compressor piston function is carried out by the adiabatic bouncing piston. In this patent drawings the space above the heat exchanger actuating mechanism or "cold finger" on the right is comprised of an air spring type buffer space rather than being open to atmosphere. An additional possibility that just crossed my mind: An air tube (blue on right) could be attached to the top of the counterbalance cylinder and positioned near the top of the compressor piston tube to take some advantage of the pressure changes taking place there. As the large ball/piston drops, the pressure in the tube above the piston will tend to fall. The slight vacuum would help with the pivot arm motion, likewise, the increase in pressure above the large piston when it bounces back upward should assist the motion of the smaller piston. I just noticed I had misspoken there, but too late to edit. When the regenerator moves down, the air flows up through it. When the regenerator (heat exchanger) moves up, the air flows back down through it.

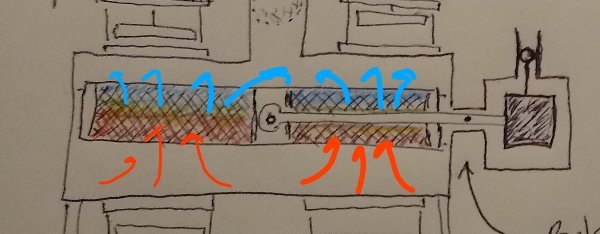
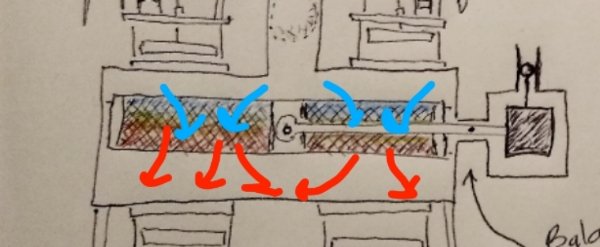
Focusing attention on the lower large chamber with the heat exchanger, and the movements of the heat exchanger: When the ball/piston falls and the pressure increases the regenerative heat exchanger is lifted upwards due to the increase in pressure, (acting on the little ball attached to the pivot arm counter balanced weight), relative to atmospheric pressure. Such upward motion while the air is being heated by the heat of compression results in heat being taken up from the hotter compressed air by the cooler regenerator mesh material that the air is passing through as the heat exchanger moves upward through the chamber. When the piston "bounces" back upward and the pressure drops the heat exchanger is lowered down through the now cooler expanded air. The heat is released from the now hotter heat exchanger back to the now colder air. The heat is returned. Always, as the adiabatic bouncing of the piston continues, the heated and cooled portions of the air in the chamber are kept separated.

The pivot arm is designed in such a way that the regenerative heat exchanger stays horizontal as it is lifted and lowered.