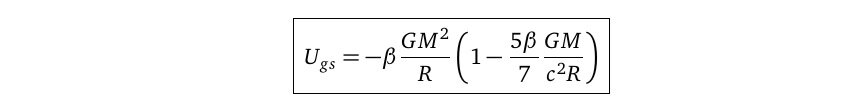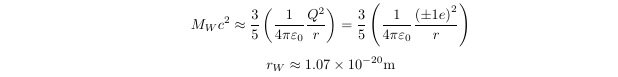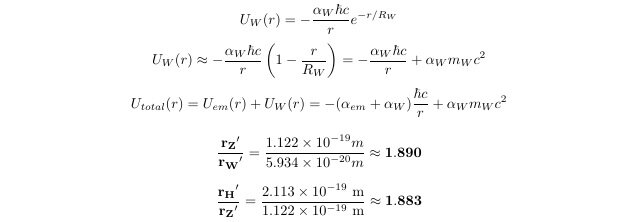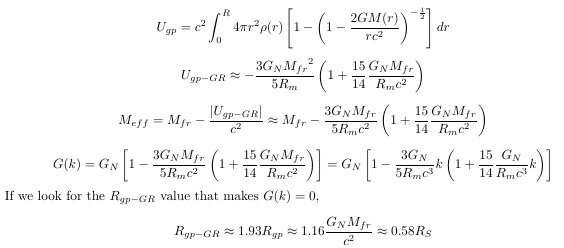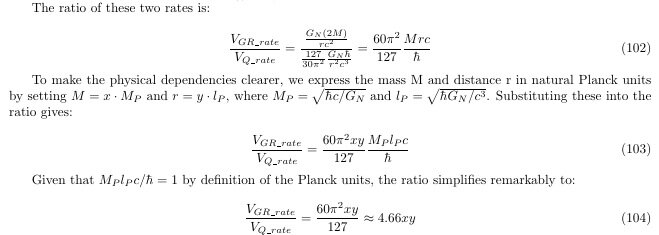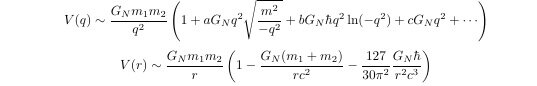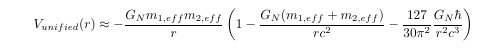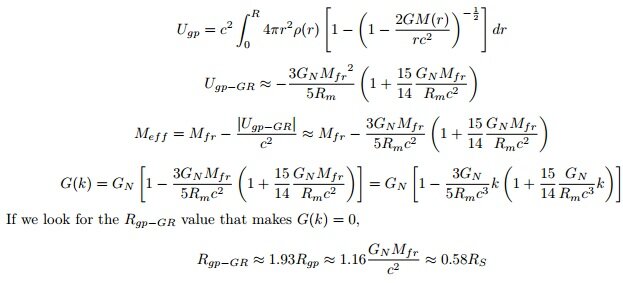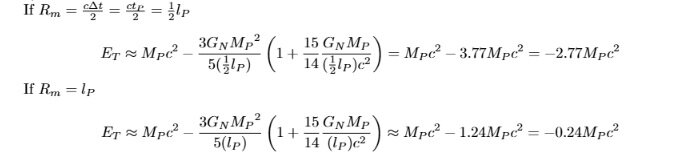icarus2

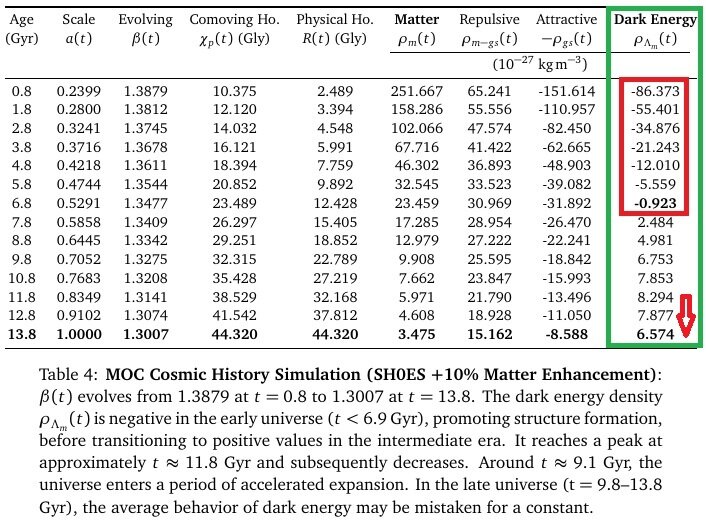
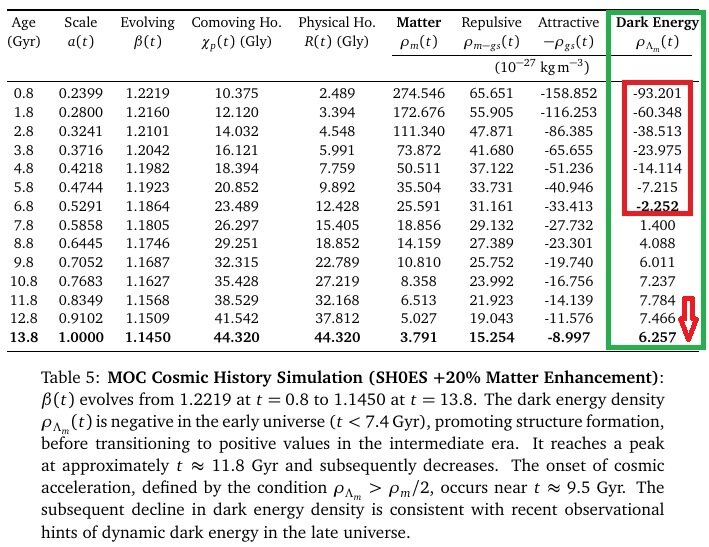
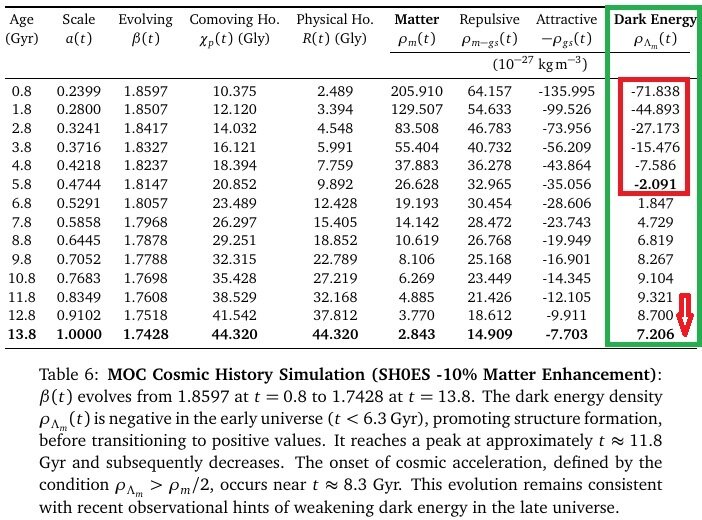
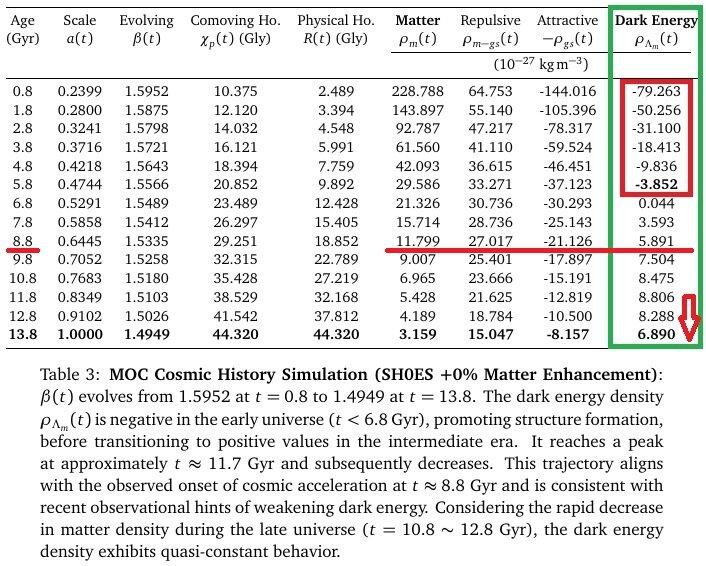
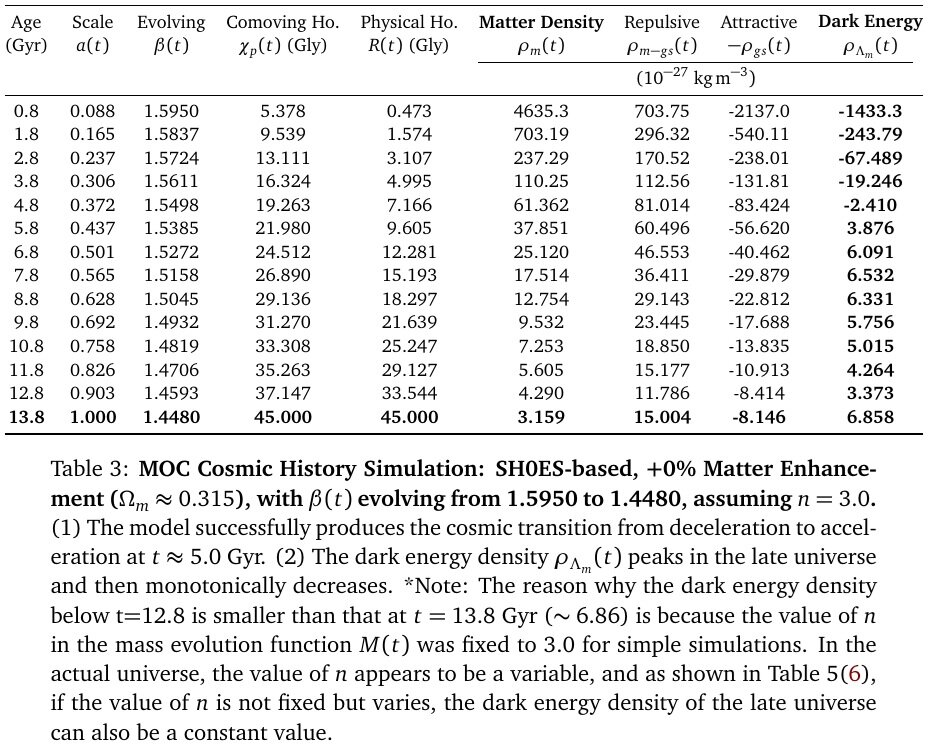
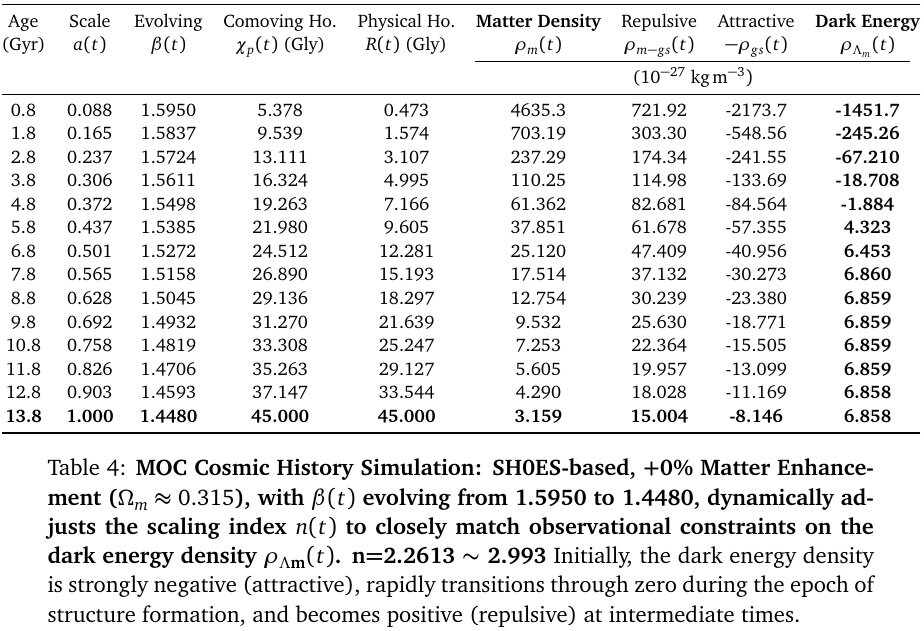
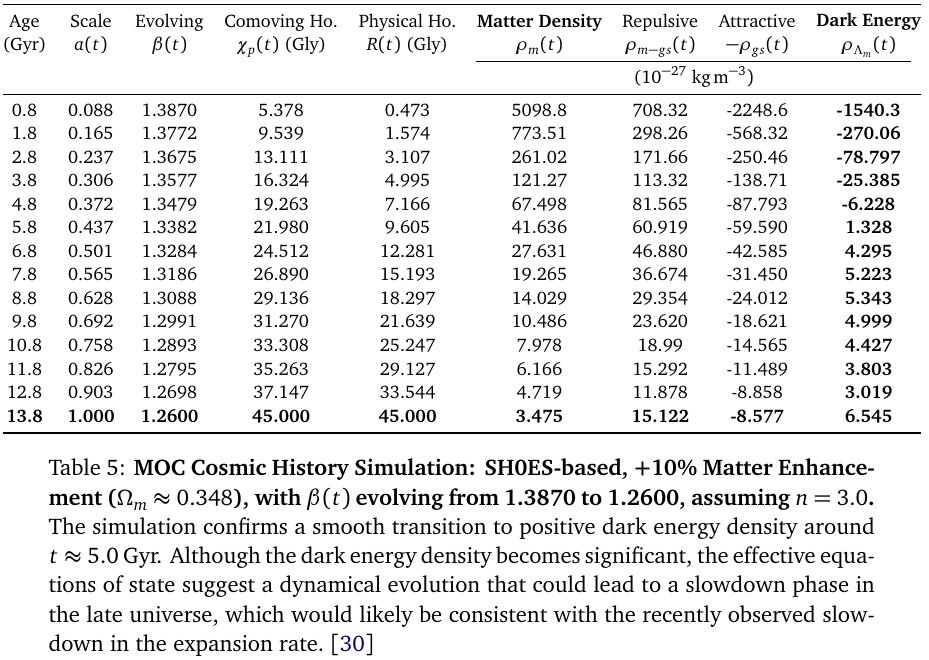
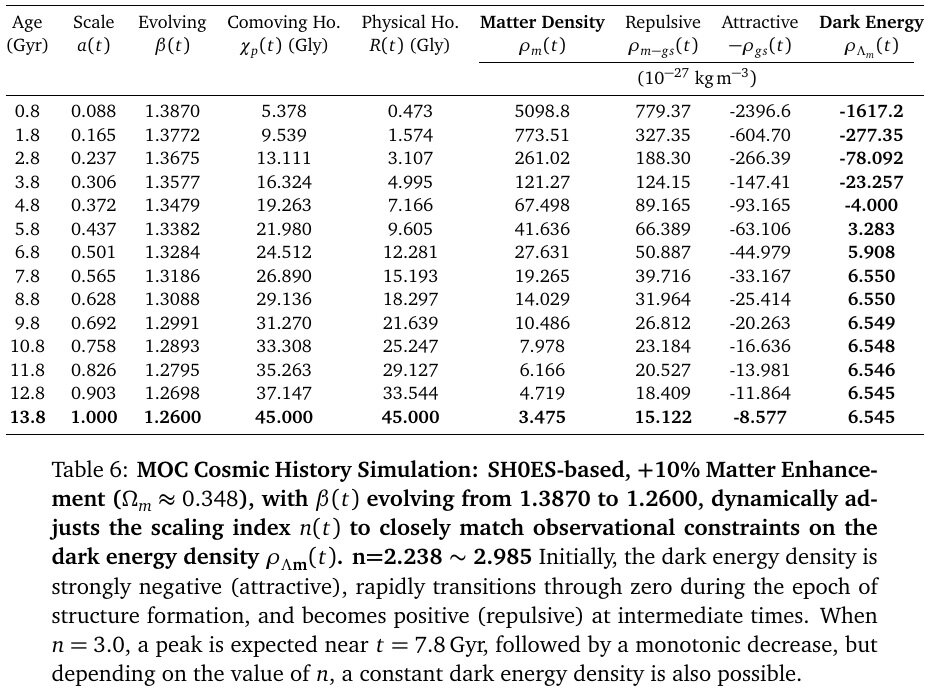
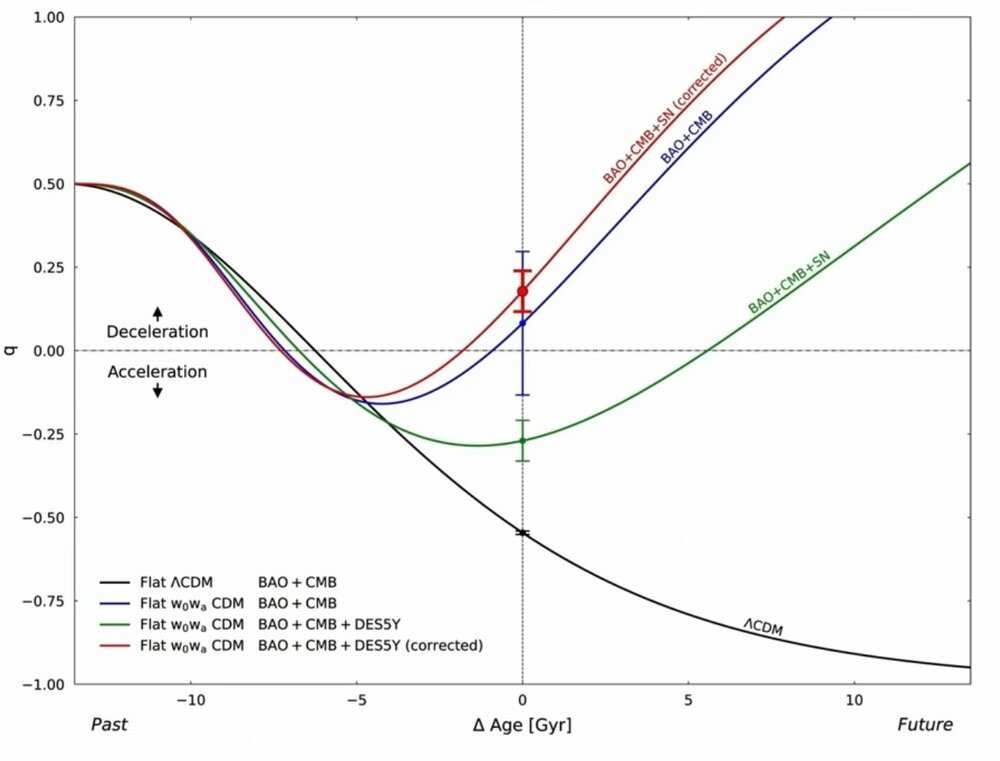
Recently, several more simulations were performed, and modifications were made to the comoving horizon, resulting in more complete results. General Characteristics of the Data: Across various simulations, the dark energy density is negative in the early universe (t < 6 Gyr, z>1.0), transitions to positive values in the middle epoch to contribute to cosmic accelerated expansion, peaks at approximately 11.8 Gyr, and subsequently decreases. This demonstrates that ρ_{Λ_m} can explain the current value of dark energy density. The dark energy equations suggest damped oscillations, and the cycles of decelerating and accelerating expansion are predicted to become longer and longer. Assuming w=-1 for dark energy, as in the ΛCDM model, the condition for accelerated expansion in the acceleration equation is ρ_m - 2ρ_{Λ_m}<0, which occurs when the dark energy density exceeds 50% of the matter density. From the data avobe, we can see that the accelerated expansion of the universe occurs around 8.8 Gyr (approximately 5 billion years ago). This total gravitational self-energy corresponds to the key characteristic of dark energy. 1) Current dark energy sign and density values 2) The point at which the universe transitioned to accelerated expansion: Around t=8.8 Gyr (approximately 5 billion years ago) 3) Recent decrease in dark energy: All simulations show a peak around t=11.8 Gyr and then a decrease. 4) The problem of massive galaxies in the early universe: In the early universe, dark energy was negative, contributing to the decelerating expansion and thus promoting the formation of galaxy structures. In particular, the prediction of a sign change in dark energy is remarkable. Gravitational self-energy resolves the problems of dark energy and inflation through a single equation within the framework of existing physics, without introducing new fields, new particles, or any free parameters. The structure parameter β is a coefficient derived from the calculation of gravitational self-energy and is not a free parameter. Because the function of dark energy is clearly defined, countless verification methods exist. Matter-Only Cosmology: A Unified Origin for Inflation and Dark Energy

Gravitational Self-Energy: A Unified Origin for Inflation and Dark Energy The standard cosmological model, ΛCDM, introduces a mysterious component known as Dark Energy (Λ), which accounts for approximately 68% of the total energy, to explain the accelerated expansion of the universe. However, the physical nature of dark energy remains unknown. Furthermore, the model faces significant challenges, including the catastrophic discrepancy between theoretical predictions and observed values (the Cosmological Constant Problem), the recently highlighted Hubble Tension, and the problem of massive galaxies in the early universe. This paper proposes the Matter-Only Cosmology (MOC) model, which argues that "dark energy is not a separate, mysterious component, but rather originates from the Gravitational Self-Energy (GSE) inherent to Matter itself." This model does not introduce new particles or fields but explains the history of the universe, from primordial inflation to late-time accelerated expansion, unifyingly through the interaction between matter and gravity alone. Here, "Matter-Only" does not imply the absence of radiation; rather, it signifies that dark energy is not a new fluid independent of matter, but a dependent energy arising directly from matter. 1. Derivation of the Complete Gravitational Self-Energy Equation Since the existing equation for gravitational self-energy is incorrect, we must derive a complete expression for gravitational self-energy. (Please refer to the paper for the detailed derivation.) Our fundamental postulate is that the source term M'(r) must be replaced by an equivalent mass M_{eq}(r), which includes not only the material mass but also the equivalent mass of its own gravitational self-energy, M'_{gs}(r). Because the mass inside the shell is not free state, but already bound. M_{eq}(r) = M'(r) - M'_{gs}(r) For a general mass distribution, we define the GPE of the inner sphere of radius r and mass M'(r) using a structural parameter β. This parameter encapsulates the geometric distribution of mass and relativistic corrections, ranging from β = 3/5 for a uniform sphere in Newtonian mechanics to values in the range of β ~1.0 - 2.0 for various astrophysical configurations in General Relativity. By integrating this equation and replacing the Newtonian coefficient of 3/5 with β to reflect general relativistic effects and the structural evolution of the universe, we obtain the following final expression. The first term (U_gs) corresponds to the conventional gravitational binding energy we are familiar with, while the second term (U_{m-gs}) represents the newly discovered interaction term between gravitational self-energy and matter. 2. Identifying the New Gravitational Self-Energy Equation with Dark Energy The total mass density of a gravitational system consists of the mass density of matter plus the mass density term due to gravitational self-energy. This gravitational self-energy corresponds precisely to dark energy. ρ_T = ρ_m + ρ_{m-gs} - ρ_{gs} = ρ_m + ρ_{Λ_m} By dividing the potential energy terms derived above by the volume, we obtain the expression for mass density. The dark energy term ρ_{Λ_m} = ρ_{m-gs} - ρ_{gs} is given as follows Examining the dark energy term, we can see that it is a function of the matter density ρ_m. Dark energy is not an independent entity but arises from matter itself. 3. Numerical Analysis of ρ_{Λ_m} Characteristics To investigate whether this ρ_{Λ_m} equation exhibits characteristics similar to the current dark energy, we performed numerical calculations. General Characteristics of the Data: Across various simulations, the dark energy density is negative in the early universe (t < 5 Gyr), transitions to positive values in the middle epoch to contribute to cosmic accelerated expansion, peaks at approximately 7 ~ 9 Gyr, and subsequently decreases. This demonstrates that ρ_{Λ_m} can explain the current value of dark energy density. Furthermore, several characteristics align with recently published results regarding the properties of dark energy. Refer to BAO+CMB, BAO+CMB+SN or BAO+CMB+SN(corrected) 4. Interpretation of Numerical Results 1) Natural Resolution of the Hubble Tension Problem: The persistent discrepancy between the Hubble constant (H_0) measured in the early universe (CMB) and the late universe (SH0ES). Solution: MOC argues that the structural parameter β evolves as cosmic structures form. Since the physical state of the early, uniform universe (β ~ 1.39; Ω_m=0.346 model) differs from that of the current, clustered universe (β ~ 1.27; Ω_m=0.346 model), attempting to describe expansion with a single constant causes the tension. Thus, the Hubble Tension is not an error but evidence of the structural evolution of the universe. 2) Resolution of the Early Massive Galaxy Problem (JWST Observations) Problem: The James Webb Space Telescope (JWST) has discovered massive galaxies formed much earlier than expected. Solution: MOC provides a crucial prediction that differs from the standard ΛCDM model. In the early universe, there existed a phase where the dark energy density was negative, implying a period with a negative cosmological constant. According to MOC, in the early universe (z > 1.5), dark energy was negative energy. This acted to enhance gravity (attraction), allowing matter to clump together much faster than predicted by existing theories. 3) Weakening Dark Energy Observation: Recent observations from DESI and others suggest the possibility that dark energy is not constant but weakens over time. Solution: In MOC, dark energy is not a constant; it possesses dynamic properties where it gradually decreases after initiating accelerated expansion. This is in exact agreement with recent observational trends. 5. Applicability to Inflation and Black Hole Singularity Problems 1)Inflation: To explain inflation, we don't introduce new elements, such as inflaton fields or false vacuums. The previously derived equation for the dark energy density ρ_{Λ_m} also applies to inflation. Even in the Planck era of the early universe, ρ_{Λ_m} was approximately 40 times larger than the matter density ρ_m. Since ρ_{Λ_m} had a positive value during this period, it drove the accelerated expansion (inflation) of the universe via negative pressure. Furthermore, the ρ_{Λ_m} equation contains a natural self-termination mechanism for inflation. 2)Black Hole: In the case of black holes, it can be mathematically verified that when R is smaller than a critical radius R_gs, the dark energy density generates a repulsive force, which prevents the formation of a singularity. 6. Conclusion Gravitational self-energy resolves the problems of dark energy and inflation through a single equation within the framework of existing physics, without introducing new fields or particles. When deriving the equation for gravitational self-energy, the mass inside a shell must be the equivalent mass that includes negative binding energy. However, by using the free-state mass M_fr instead of the equivalent mass, we have been led down the wrong path. Consequently, this oversight has given rise to various problems related to gravity, such as inflation, dark energy, singularities, and divergences. #Paper: Matter-Only Cosmology: A Unified Origin for Inflation and Dark Energy

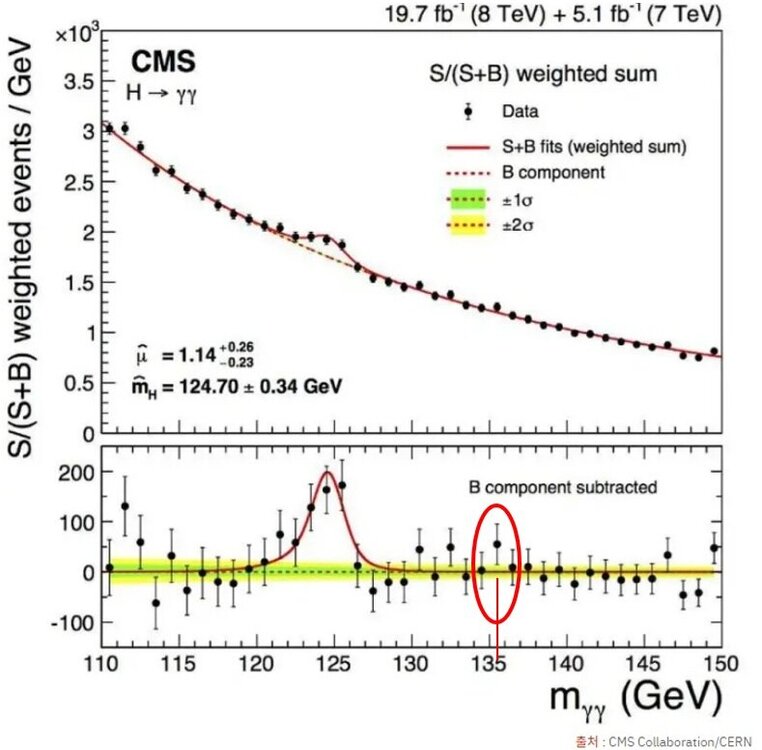
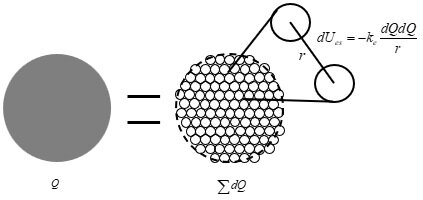
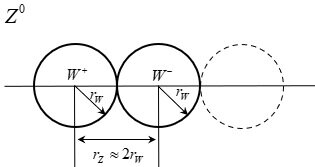
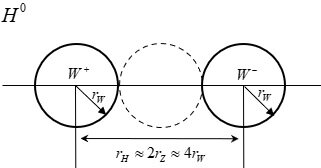
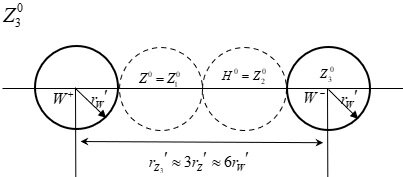
The 125 GeV H0 is not the Higgs particle but the first excited state of the W+W- composite particle! 1. The Crisis of the Higgs Mechanism The discovery of a particle identified as the Higgs boson at approximately 125 GeV has been hailed as a great triumph of the Standard Model. However, the Higgs mechanism (Mexican hat potential --> Spontaneous symmetry breaking --> Higgs field --> Mass generation) still harbors several serious issues. 1) Hierarchy/Naturalness Problem: The mass of the Higgs boson is expected to receive enormous quantum corrections, potentially driving it up to the Planck scale. For the mass to remain at 125 GeV, the "bare mass" must be fine-tuned with an almost unbelievable precision to nearly perfectly cancel out these corrections. 2) Vacuum Energy Catastrophe: This is the most significant problem. The Higgs field, which has a non-zero value in the vacuum, predicts an energy density for empty space that is approximately 10^55 times larger than the cosmologically observed value. The Higgs mechanism cannot function without assuming an energy density for the vacuum (Higgs field). Assuming the energy density required by the Higgs mechanism not only contradicts observations but also leads to a catastrophic scenario for the universe. A fine-tuning of 10^55 is not only unreasonable but also introduces a new problem: the existence of enormous initial energy if such fine-tuning is assumed. This is a critical issue that physicists unanimously agree must be resolved. 3) Other Issues: The Higgs mechanism faces additional challenges, including the arbitrariness of the Yukawa coupling constants, the hierarchy of the mass spectrum, the unexplained origin and form of the Higgs potential, the arbitrariness of the Higgs boson’s mass, the asymmetry between leptons and quarks, the lack of integration with dark matter and dark energy, the vacuum stability problem, the strong CP problem, and the difficulty of reconciling the mechanism with quantum gravity, all of which suggest the need for new physics beyond the Standard Model. 2. Hypothesis: The Majority of Mass Originates from Intrinsic "Self-Energy" This paper proposes a more fundamental principle, rooted in classical physics and calculus, regarding the origin of mass. The mass of fundamental particles arises from the particle's self-energy. Since the (electromagnetic, strong, weak) charge Q is a collection of infinitesimal charges dQ, there exists potential energy due to these dQ charges (electromagnetic, strong, weak). The potential energy between like (electromagnetic, strong, weak) charges is positive energy, so the existence of the charge itself results in positive energy and positive mass. The picture above is an example of a electromagnetic charge. This idea posits that all particles with (electromagnetic, weak, strong) charges can be viewed as a charge distribution spread out in space. Consequently, potential energy exists between the infinitesimal charges constituting the charge distribution, and according to E=mc^2, an equivalent mass corresponding to this potential energy exists. I believe this principle, derived from calculus, is more fundamental than assuming an arbitrary "Mexican hat" potential designed merely to produce desired results. This self-energy model avoids the problems arising from the introduction of the Higgs field, as it does not require an external field like the Higgs field for fundamental particles to acquire mass. The self-energy model due to the existence of such charges is known not to work well for free leptons, possibly due to environmental factors. Quarks, being confined, are permanently bound within hadrons. They also constantly interact with other quarks and gluons. This continuous interaction environment acts as a form of continuous "quantum measurement", forcing the quark's wave function to localize. As a result, a well-defined effective radius is maintained. In contrast, free leptons like electrons are fundamentally different. Unlike quarks, electrons are not subject to confining forces that continuously localize their position. Without such forces, the wave function spreads significantly, making a classical, stable radius unclear. Therefore, applying the self-energy model is challenging. Consequently, the mass of a free electron is better explained from the perspective of Quantum Electrodynamics (QED), where the "bare mass" is obscured by vacuum polarization or screening effects. 3. Key Result: Z0 and H0 Are the Ground State and First Excited State of the W+W- Composite System The central claim of this paper is that the Z0 and H0 bosons are not distinct fundamental particles but rather the ground state and the first excited state of a single composite system, namely a pair of W+ and W- bosons. The evidence lies in the fact that three independent physical principles align perfectly with this hypothesis. Furthermore, a key result is the relationship r_H ~ 2r_Z ~ 4r_W, meaning that the radii of the 125 GeV H0, Z0, and W particles are related by near-integer multiples, suggesting this is more than a mere coincidence. 1) Charge Conservation: The proposed constituent particles, W+ (charge +1e) and W- (charge -1e), when combined, yield a net charge of zero. This is consistent with the neutral charge observed in both the Z0 and H0 bosons. 2) Energy Conservation: The mass of a composite particle is the sum of the masses of its constituent particles plus the binding energy. Since the two W particles carry charges, the binding energy includes electromagnetic potential energy. For an intuitive explanation, the results are initially derived assuming only electromagnetic potential energy. The paper extends this by incorporating both electromagnetic potential energy and the potential energy of weak interactions to obtain the results. (M_composite)c2 = (M_W++ M_W-)c2 + U_binding Z0 (graound-state): U_{binding,Z} = 91.188GeV - 2(80.379GeV) = - 69.570GeV (M_Z)c^2 = 2(80.379GeV) - 69.570GeV = 91.188GeV H0 (first-excited-state): U_{binding,H} = 125.100GeV - 2(80.379GeV) = - 35.658GeV (M_H)c^2 = 2(80.379GeV) - 35.658GeV = 125.100GeV This result is profoundly significant. The binding distance of the H0 state is nearly twice that of the Z0 state. As demonstrated in the paper, this quantized relationship remains robust even in a more comprehensive model that includes the weak force potential (ratio ~1.88). Such an integer-multiple relationship strongly suggests that these particles are not independent but rather two different quantum states of the same system. When the weak force potential is included, a Yukawa potential term for the weak interaction is added, as shown below. Even in a model that includes both electromagnetic and weak forces, the relationship r_H' ~ 2r_Z' ~ 4r_W' approximately holds. 3) Spin: The critical test is whether this model can account for the different spins of Z0 (spin-1) and H0 (spin-0). According to quantum mechanics, when two spin-1 particles (W+ and W-) combine, the total spin can be S=0,1,2. This model proposes the following: - Z0 (S=1): A "triplet state" where the spins of the W bosons are aligned in parallel. This is a natural low-energy configuration consistent with the ground state. (Spin of W+: ↑) + (Spin of W-: ↑) -->(Total Spin of Z0: S=1) - H0 (S=0): A "singlet state" where the spins are aligned in opposite directions, canceling each other out. This different quantum configuration naturally corresponds to a different energy level (excited state). (Spin of W+: ↑) + (Spin of W-: ↓) -->(Total Spin of H0: S=0) 4. New Prediction: A Second Excited State Exists near ~135.4 GeV This model provides specific and falsifiable predictions, namely the existence of the second excited state of the W+W- system. Based on the energy level spacing, it predicts a new neutral resonance particle with a mass of approximately 135.4 GeV. Detecting this particle at the LHC or future particle accelerators will serve as a critical test of this hypothesis. Although no definitive signal for a ~135.4 GeV resonance has been reported so far, this may be due to the low production probability of such a second excited state. Intriguingly, some public plots from CMS have shown minor, statistically insignificant excesses in the mass region around 135.5 GeV. While these could be mere statistical fluctuations, they align remarkably with our model's pinpoint prediction of 135.4 GeV. This alignment provides a compelling motivation for experimental groups to perform a dedicated search within this specific mass window, as the discovery of such a resonance would provide powerful evidence for the composite nature of electroweak bosons. Given that there are now some logical grounds (five in total: 1)the existence of mass based on the principle of calculus, 2)charge, 3)energy, 4)spin, and 5)r_H' ~ 2r_Z' ~ 4r_W') for predicting a new particle near 135.4 GeV, viewing events in this energy range with a perspective of greater possibility may lead to alternative interpretations of existing data. 5. Conclusion In conclusion, this paper asserts that the 125 GeV particle discovered at the LHC is not a fundamental Higgs boson but rather the first observed excited state of the W+W- system. In this model, the artificial "Mexican hat potential" and "Higgs field" introduced to endow W+, W-, and Z0 with mass are unnecessary. This is because W+ and W- acquire mass due to the existence of their (electromagnetic, weak) charges, and Z0 acquires mass from both the (electromagnetic, weak) charge-induced mass and the binding energy. If this claim is correct, the Mexican hat potential, the Higgs field, and the vacuum energy associated with the Higgs field become superfluous constructs. This approach resolves severe issues, such as the vacuum energy catastrophe, by explaining mass through the more fundamental principles of self-energy and composite particle dynamics. #Paper: The Z0 and H0 Bosons as the Ground and First Excited States of a W+W− System

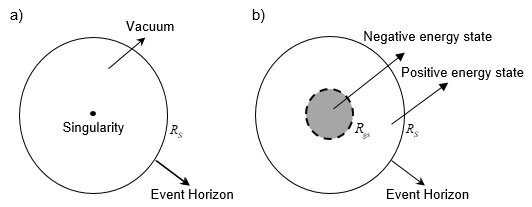
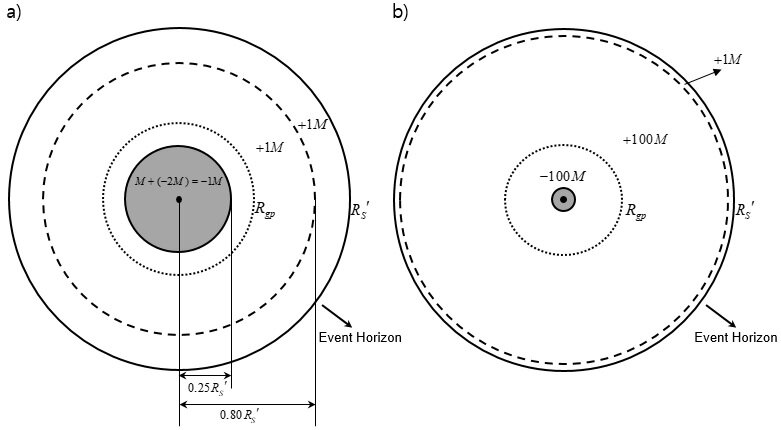
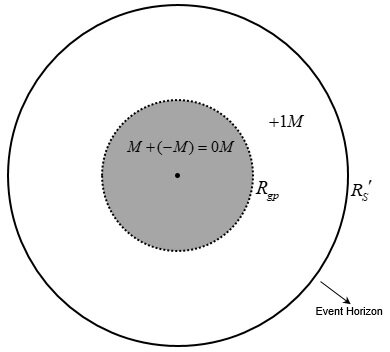
A Model for the Interior State of a Black Hole The process of releasing binding energy during gravitational contraction is inherently complex. However, for a general analysis, the core principle is that for a system to settle into a more stable, tightly-bound state, it must radiate away an amount of energy equivalent to the change in its gravitational potential energy. This results in a corresponding decrease in the system's total equivalent mass. If we consider a rotating mass distribution, the virial theorem suggests that approximately half of the change in binding energy contributes to this reduction in the system's equivalent mass. While differential rotation adds further complexity, the exact numerical factors are not critical to the core argument, so we will omit them for this analysis. For now, let's consider the non-rotating case, keeping in mind that the inclusion of rotation would likely result in a smaller critical radius (R_gs) than the non-rotating case (perhaps by a factor between 0.5 and 1). The release of binding energy external to a black hole is a well-understood process, so we can omit that discussion. Instead, let's focus on the problem of gravitational contraction and energy release inside a black hole. Simplifying the Problem: The Low-Density Black Hole Analogy The interior problem becomes exceedingly complex when considering ultra-high-density black holes, as it seems to require a full theory of General Relativity and quantum mechanics. However, it's well-known that the concept of a black hole is not exclusive to ultra-dense objects. To simplify the analysis, it is useful to first consider a sufficiently large black hole and then extrapolate the findings to higher-density cases. For example, a supermassive black hole of about 4 billion solar masses has an average density comparable to that of Earth's air (~1.225 kg/m³). Conceptually, we can therefore picture this as a "black hole made of air." Simplifying the Problem: The Low-Density Black Hole Analog The interior problem becomes exceedingly complex when considering ultra-high-density black holes, as it seems to require a full theory of General Relativity and quantum mechanics. However, it's well-known that the concept of a black hole is not exclusive to ultra-dense objects. To simplify the analysis, it is useful to first consider a sufficiently large black hole and then extrapolate the findings to higher-density cases. For example, a supermassive black hole of about 4 billion solar masses has an average density comparable to that of Earth's air (~1.225 kg/m³). Conceptually, we can therefore picture this as a "black hole made of air." Contraction Inside the "Air Black Hole" Now, let's analyze the gravitational contraction of this "air" inside the black hole. The critical radius (R_gs) at which the negative gravitational self-energy precisely cancels the positive rest mass energy can be estimated: In a Newtonian approximation, this radius is R_gs ≈ 0.3R_S, where RS is the Schwarzschild radius. In General Relativity, accounting for the virial theorem and rotation, the radius is approximately R_gs ≈ 0.51R_S. While the values differ, the fundamental logic is the same. For the sake of clarity, I will proceed using the Newtonian result R_gs = 0.3R_S. Consider the scenario where the "air," initially distributed out to R_S, undergoes gravitational contraction down to the radius R_gs. In this final state, the "system" is the sphere defined by 0 ≤ r < R_gs. The surrounding shell, R_gs < r < R_S, now effectively becomes the "exterior" relative to this new, contracted system. Crucially, the binding energy released during this contraction is not ejected from the black hole itself. Instead, it is radiated into this exterior shell. Therefore, the total mass and energy of the black hole as a whole (out to R_S) remain conserved. The State of the Zero-Energy System What, then, is the state of the system within the radius RgsRgs? Its total energy is zero: E_T = M_frc^2 - (3/5)G(M_fr)^2/R_gs = 0 However, a total energy of zero does not imply a vacuum or an absence of matter. This state is not an empty E_T = 0 + 0 = 0. Rather, it is a state where matter M and its associated negative gravitational potential energy coexist, with their sum being zero. Since matter M is still present, it can exhibit all the properties of matter, such as thermal radiation. At any local point occupied by the "air," the local energy density is still positive. This is because the rest mass energy of the air particles in an infinitesimal volume is greater than the negative gravitational potential energy contained within that same volume. It is only the total energy of the entire system (from r=0r=0 to RgsRgs) that integrates to zero. Consequently, the net gravitational influence of this zero-energy system on an external observer is null. To put it another way, this state can be visualized as islands of positive-mass "air" existing within a sea of negative gravitational energy. This is analogous to our own universe, where the total energy of dark energy is vast, yet in the local vicinity of planets and galaxies, the matter-energy density is significantly higher than that of the surrounding dark energy. For a more in-depth treatment of the black hole interior problem, I recommend consulting the following paper. https://www.researchgate.net/publication/313314666_Solution_of_the_Singularity_Problem_of_Black_Hole *In previous black hole papers, R_gp was used instead of R_gs. R_gs=R_gp. Figure 2: Internal structure of a black hole according to the radius of the mass distribution a) Existing Model. b) New Model. The area of within R_gp (or R_gp-vir) has gravitational self-energy (potential energy) of negative value, which is larger than mass energy of positive value. If R is less than R_gp(or R_gp-vir), this area becomes negative energy (mass) state. There is a repulsive gravitational effect between the negative masses, which causes it to expand again. This area (within R_gp(or R_gp-vir) exercises anti-gravity on all particles entering this area, and accordingly prevents all masses from gathering to r=0. Therefore, the mass (energy) distribution cannot be reduced below the radius R_gp (or R_gp-vir). Figure 6: Temporarily, when the mass M contracts more than R_gp, the central region of the black hole becomes a negative mass state. a) is the case where the mass M is compressed into a region smaller than R_gp, and the negative gravitational potential energy corresponds to -2Mc^2. In this case, the total energy of the system (0 ≤ r ≤ R) will be -1Mc^2, and the total energy outside (R < r ≤ R_S' ) the system will be 2Mc^2. The total energy inside the black hole will remain +1Mc^2. b) is a case where the mass M is compressed into a smaller region, so that the total energy of the system (0 ≤ r ≤ R) is -100Mc^2, and the total energy outside (R < r ≤ R_S' ) the system will be +101Mc^2. R is a value obtained through calculation in individual situations. Figure 7. Over time, when the energy distribution inside the black hole is stabilized, the internal structure of the black hole. The 0 ≤ r ≤ R_gp region is a region where the positive mass energy and the negative gravitational potential energy have the same size, and the total energy is 0. The released binding energy exists in the region outside R_gp. The total mass of the black hole is M. The mass or energy distribution at the center of a black hole is, M + (-M)=0; M(Equivalent mass of matter and energy) + (-M)(Equivalent mass of gravitational self-energy) = 0 So, how can we determine if the internal structure of a black hole is as described? Can it be proven? My answer is yes. I believe and argue that this internal structure of a black hole can be proven. The basis for this claim is my hypothesis that our own universe is structurally analogous to the interior of a black hole. Consequently, I propose that the universe we observe today is, in fact, a direct representation of what the inside of a black hole looks like. We reside within an exceptionally large black hole, and it is because we are currently located in the region where R < R_gs that we experience an accelerating expansion of the universe. ==== We live inside a black hole. I think that the accelerated expansion of the universe and the dark energy effect are evidence that we live inside a black hole. Therefore, I claim that by verifying the dark energy term, we can prove that we live inside a black hole. You may think that the Hubble-Lemaitre expansion of the universe conflicts with the Black Hole Cosmology, but before you make a definitive judgment on this, let's hear a little more! 1.The size of the event horizon based on the total mass of the observable universe According to Shell Theorem and Birkhoff’s Theorem, in a spherically symmetric system, the gravitational effect at a given radius is determined only by the mass or energy content surrounded within that radius, and contributions from outside the shell do not affect the internal dynamics. R_obs=46.5Gly ρ_c=8.64x10^-27kgm^-3 R_S=2GM/c^2=491.6Gly The size of the event horizon created by the total mass distribution of the observable universe is 491.6 Gly. The event horizon created by the total mass of the observable universe is roughly 10 times larger than the observable universe. Therefore, the observable universe exists inside the event horizon of a black hole created by its own mass. There are several fatal weaknesses in this black hole cosmology. 2.Weaknesses of the Black Hole Cosmology 1) In a black hole, all matter is compressed into a singularity, so there is no space for humans to live. There is no almost flat space-time that could contain the observable universe inside a black hole. 2) In the black hole, singularity exist in the future, and in the universe, singularity exist in the past. Black hole and the universe are opposites. 3) The universe is expanding. Inside a black hole, all matter must contract to a singularity. The two models show opposite phenomena. It is difficult to explain the expansion of the universe inside a black hole. In addition, the universe is expanding at an accelerated rate. Problems such as strong tidal force enough to disintegrate people, the movement of all matter in the direction of the singularity, and the expanding universe have been pointed out as fatal weaknesses of the Black Hole Cosmology. If our universe was a black hole, all galaxies should have collapsed into a singularity or exhibit motion in the direction of the singularity, but the real universe does not exhibit such motion characteristics. Therefore, the Black Hole Cosmology was judged to be inconsistent with the current observations, and the Black Hole Cosmology did not become a mainstream cosmological model. Although this objection (Weaknesses) appears to be clear and well-grounded, in fact, this objection also has its own fatal weaknesses. Most physicists and astronomers believe that the singularity problem will be solved by quantum mechanics or some other unknown method. In other words, most scientists think that singularities don't exist. They are using it as a basis for criticism, even though they think that singularity will not exist. We think that the singularity problem will ultimately be solved by some mechanism. Therefore, in the process of solving the singularity problem, there is a possibility that the singularity problem of the Black Hole Cosmology will also be solved. For the singularity to disappear, there must be a repulsive force inside the black hole. Due to this repulsive force, an uncompressed region inevitably exists inside the black hole. The remaining question is, 'Can the uncompressed region be larger than the observable universe?' If the singularity disappears due to quantum mechanics, the uncompressed region will be very small compared to the observable universe. But what if the singularity disappears by some other means than quantum mechanics? ~~~~~~ A full exposition of this 'Black Hole Cosmology' is too extensive for this post. However, for those interested, I invite you to read the article at the link below. Additionally, Chapter 7 of the 'Sphere Theory' paper referenced in the main text provides further detail. https://www.reddit.com/r/blackholes/comments/1icshzw/we_live_in_a_black_hole_the_accelerated_expansion/

Your argument rests on a fundamental misapplication of Birkhoff's theorem. You are incorrectly extending it to dynamic, energy-radiating processes as if the total mass of the system were immutable. 1)Birkhoff's Theorem Describes a State, Not a Process: The theorem states that the external spacetime of a spherically symmetric mass is the Schwarzschild metric for a given total mass, M. It does not state that M must remain constant if the system radiates energy. 2)Binding Energy and Mass Defect are Real: Any system that becomes more tightly bound radiates energy and, as a consequence of E = mc², loses mass. This is a well-established fact, observable from the atomic scale to the cosmological: Hydrogen Atom: A hydrogen atom's mass is less than the sum of a free proton and a free electron because ~13.6 eV of binding energy is released. The Earth: Earth's mass is little less than the mass of its constituent dust and gas in a dispersed state, as gravitational potential energy was radiated away as heat during its formation. Gravitational Contraction is a Dynamic Process. When a star contracts, it radiates energy (as photons, neutrinos, etc.) to become more gravitationally bound. This process is inherently non-static. The initial mass (M) decreases to a new, final mass (M') because energy has left the system. Birkhoff's theorem applies perfectly to the initial state (with mass M) and to the final, more stable state (with mass M'). However, it does not forbid the transition from M to M'. Your claim that the total mass remains unchanged contradicts the law of conservation of energy. Please consider the mass reduction of a hydrogen atom or Earth due to binding energy.

It is not possible to explain every detail in the summary, and the point you raised is, in fact, a matter of common knowledge. It is widely understood that, during gravitational contraction or orbital transitions, energy corresponding to the difference in binding energy must be released to the outside of the system in order to achieve a stable bound state. Therefore, I did not consider it necessary to elaborate on this in the summary. However, this point is briefly mentioned in the main body of the paper. ==== In gravitationally bound systems, changes in configuration (e.g., orbital reduction) lead to a decrease intotal energy and equivalent mass due to energy radiation, as seen in celestial mechanics [8]. ~~~ Even if we apply the kinetic energy and virial theorem, the radius only decreases as negative energy cancelsout positive energy, but the core claim that “there is a point where the negative gravitational potential energycancels out the positive mass energy.” remains unchanged. Although potential energy changes to kinetic energy, in order to achieve a stable bonded state, a part of the kinetic energy must be released to the outside of thesystem ~~~ If you cannot accept the negative energy state, please refer to the following explanation.If, R_m = R_{gs−NM} , the total energy of the system, including the gravitational potential energy, is From the point of view of mass defect, r = R_{gs−NM} (or R_{gs−NM−vir}) is the point where the total energy ofthe system is zero. For the system to compress more than this point, there must be an positive energy release from the system. However, since the total energy of the system is zero, there is no positive energy that thesystem can release. Therefore, the system cannot be more compressed than r = R_{gs−NM} (or R_{gs−NM−vir}). Soblack hole doesn’t have singularity ~~~ Applying the core principle of Sphere Theory, which posits that total energy includes self-energy, even if some particle comes into the radius of black hole, it is not a fact that it contracts itself infinitely to the point R = 0. From the point R_{gs−NM} (or R_{gs−NM−vir}), gravity is 0, and when it enters into the area of R_{gs−NM} (or R_{gs−NM−vir}), total energy within R_{gs−NM} (or R_{gs−NM−vir} ) region corresponds to negative values enablinganti-gravity to exist. This R_{gs−NM} (or R_{gs−NM−vir} ) region comes to exert repulsive effects of gravity on the particles outside of it, therefore it interrupting the formation of singularity at the near the area R = 0. However, it still can perform the function as black hole because the emitted energy will exist in a region larger than r > R_{gs−NM} (or R_{gs−NM−vir} ). Since the emitted energy cannot escape the black hole, it is distributed inthe region R_{gs−NM} (or R_{gs−NM−vir}) < r < RS_ . Since the total energy of the entire range (0 ≤ r < R_S ) insidethe black hole is positive, it functions as a black hole. ~~~

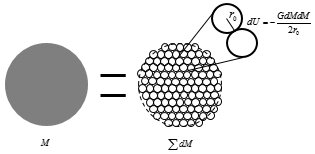
Sphere Theory: Beyond String Theory, Completing Quantum Gravity! For decades, we have been working to perfect the theory of quantum gravity, exploring radical new ideas such as extra dimensions (string theory) or the quantization of spacetime itself (loop quantum gravity). Moreover, significant unresolved problems related to gravity—such as the divergence problem, the singularity problem, the cause or driving mechanism of inflation, and the problem of cosmic accelerated expansion—span from the smallest to the largest scales. This strongly suggests that we may be missing something crucial in our understanding of gravity. Although these four representative gravity-related problems (Divergence, Singularity, Inflation, and Dark Energy ) appear to exist at different scales and in different contexts, they could, in fact, be manifestations of a single underlying issue related to gravity. That issue is the necessity of antigravity or repulsive forces. If antigravity exists in the context of gravity, all four of these problems could be resolved. If this antigravity is scale-dependent, it could address issues across different scales. I believe the physical concept that mainstream physics is overlooking is the gravitational self-energy or binding energy inherent to an object. The effective source of gravity is not the free-state mass (M_fr) but the equivalent mass (M_eq) corresponding to the total energy of the object. And this equivalent mass includes the gravitational self-energy (negative binding energy) that has a negative value. Since gravitational self-energy is negative energy, it satisfies the anti-gravity requirement. Also, since it is scale-dependent, it can solve the gravity problem from the smallest scale to the largest scale. By accounting for this gravitational self-energy, we can resolve the four aforementioned problems and complete a theory of quantum gravity. Why 'Sphere Theory'? The concept of gravitational self-energy(U_gs) is the total of gravitational potential energy possessed by a certain object M itself. Since a certain object M itself is a binding state of infinitesimal mass dMs, it involves the existence of gravitational potential energy among these dMs and is the value of adding up these. M = ΣdM. The gravitational self-energy is equal to the minus sign of the gravitational binding energy. Only the sign is different because it defines the gravitational binding energy as the energy that must be supplied to the system to bring the bound object into a free state. *To understand the basic principle, we can look at the problem in Newtonian mechanics, and for the actual calculation, we can use the binding energy formula of general relativity to find the value. U_gs=-(3/5)(GM^2)/R In the case of a spherical uniform distribution, the total energy of the system, including gravitational potential energy, is In the general case, the value of total gravitational potential energy (gravitational self-energy) is small enough to be negligible, compared to mass energy Mc^2. However, as R gets smaller, the absolute value of U_gs increases. For this reason, we can see that U_gs is likely to offset the mass energy at a certain radius. The mass defect effect due to binding energy has already been demonstrated in particle physics. Thus, looking for the size in which gravitational self-energy becomes equal to rest mass energy, At the critical radius R_gs, the negative gravitational self-energy cancels out the positive mass energy, so the total energy becomes zero, and therefore the gravity becomes zero. R_gs = (3/5)GM/c^2 (*For the detailed calculation based on general relativity, please refer to the paper.) The integration of the gravitational binding function is not analytical. Using the first-term approximation, we obtain the value R_gs-GR ~ 1.16G_NM_fr ~ 0.58R_S. If we calculate the integral itself numerically and apply the virial theorem to it, we obtain the value R_gp-GR-vir ~ 1.02G_NM_fr ~ 0.51R_S. Since the process in which actual celestial bodies contract gravitationally to become black holes is very complex, these values may be slightly different. The important thing here is not the exact value, but the fact that there exists a actual critical radius R_gs where the negative gravitational self-energy offsets the positive mass energy. It is also estimated that this R_gs exists between the radius of the black hole 0.5R_S and 1R_S. What this critical radius R_gs means is that, If the object were to shrink further (R<R_gs), it would enter a negative energy state. This generates a repulsive gravitational force ('anti-gravity'), which prevents any further collapse. Therefore, R_gs acts as an minimal radius. Nothing can be stably smaller. (This is temporarily possible, however.) This replaces the abstract 'point' particle with a fundamental, volumetric 'sphere'. Where QFT can be viewed as a “Point Theory” and String Theory as a “String Theory”, Sphere Theory is built upon the physical principle that all fundamental entities are not mathematical idealizations but physical objects possessing a three-dimensional volume. This framework, which can also be more descriptively referred to as the Gravitational Self-Energy Framework (GSEF), does not postulate new entities but rather rigorously applies a core tenet of general relativity: that all energy, including an object’s own negative self-energy, acts as a gravitational source. How is this different from String Theory? Derived vs. Postulated: String Theory postulates a fixed minimal length. Sphere Theory derives a dynamic minimal radius (R_gs) that is proportional to the object's mass. Simplicity: It requires no extra dimensions, no supersymmetry, and no new particles. It aims to solve the problem using the physics we already have. Universality: This highlights another fundamental difference in scope. String Theory's central feature is its minimal length, fixed at the Planck scale. While this offers a potential resolution for divergences at that specific scale, the challenges of gravity are not confined to the microscopic. They extend to the largest cosmological scales, where String Theory offers less clear solutions. This suggests that a theory with a fixed minimal scale may not be the fundamental framework capable of describing both domains. This is where Sphere Theory offers a profoundly different and more powerful approach. Its critical radius R_gs, is not a fixed constant but a dynamic variable proportional to mass (R_gs ∝ GM/c^2). This inherent scalability means the theory's core principle applies seamlessly from the smallest quantum fluctuations at the Planck scale to the entire observable universe. It therefore has the potential to be a true candidate for the ultimate solution to gravity, unifying the physics of the very small and the very large under a single, coherent principle. ~~~~ What problems does Sphere Theory solve? It is a foundational principle, recognized in both Newtonian mechanics and general relativity, that the effective gravitational source is the equivalent mass (M_eq), which includes gravitational self-energy (binding energy), rather than the free state mass (M_fr). This principle leads to a running gravitational coupling, G(k), that vanishes at a critical scale, R_gs ~ G_NM_fr/c^2. This behavior provides a powerful and self-contained mechanism for gravity’s self-renormalization, driving the coupling to a trivial (Gaussian) fixed point (G(k) -> 0) and rendering the infinite tower of EFT counter-terms unnecessary. The scope of Sphere Theory extends far beyond the divergence problem, providing a unified foundation for several long-standing puzzles. We demonstrate that this single principle: 1) Resolves the singularity problem via a repulsive force that emerges at a macroscopic, not quantum, scale (Section2-3). 2) Solving the 2-loop and greater divergence problem: Solve the 2-loop or greater divergence problem proposed by Goroff and Sagnoti (Section 4.6.3). 3) Solving divergence of the gravitational potential between two masses in standard EFT: It solves the divergence problem of the standard effective field theory (EFT) proposed by John F. Donoghue et al.(Section 5~6.) 4) Provides a UV completion for EFT by resolving the predictive obstacles in key quantum calculations. We resolve the divergence problems arising in (1)the gravitational potential between two masses, (2)the bending of light by applying the principle of source renormalization. This approach shows that the infinite tower of unknown EFT coefficients (c_i) is rendered unnecessary because the interaction source is dynamically quenched (M_eq} --> 0) in the UV limit, making the question of their values moot. This framework also makes a novel prediction of a "quantum-dominant regime” that distinguishes it from standard EFT (Section 5). 5) Establishes the physical origin of the Planck-scale cutoff in quantum field theory (Section 4.7). 6) Offers a unified explanation for the major puzzles of modern cosmology by providing (1)a mechanism for cosmic inflation, (2)a model for the accelerated expansion of the universe, and (3)a predicted upward revision of the neutron star mass limit (TOV limit), all of which serve as falsifiable tests (Section 7). 7) Declaration of completion of quantum gravity: Finally, it culminates in a declaration that the synthesis of EFT and Sphere Theory constitutes a complete and testable framework for quantum gravity. We will argue that this unified model, built on the physical principle of self-energy, provides the first consistent theory of gravity from the lowest to the highest energy scales (Section 8). ~~~ How can Sphere Theory be tested? This framework makes concrete, falsifiable predictions that distinguish it from standard theories: 1) A Falsifiable Prediction at the Planck Scale: It predicts a novel "quantum-dominant regime." Standard Effective Field Theory (EFT) predicts that as you approach the Planck scale, classical GR corrections will always overwhelmingly dominate quantum corrections. My paper shows the ratio of these corrections is approximately V_GR / V_Q ≈ 4.66 (M/M_P) (r/ l_P). For a stellar-mass black hole, this ratio is a staggering ~10^39, making quantum effects utterly negligible. Sphere Theory reverses this. As an object approaches its critical radius R_gs, its equivalent mass (M_eq) is suppressed, which quenches the classical correction. The quantum term, however, is not suppressed in the same way. This creates a window where quantum effects become the leading correction, a unique and falsifiable signature that distinguishes this theory from standard EFT at its point of failure. 2) At the other Scale: Offers a unified explanation for the major puzzles of modern cosmology by providing (1) a mechanism for cosmic inflation, (2) a model for the accelerated expansion of the universe, and (3) a predicted upward revision of the neutron star mass limit (TOV limit), all of which serve as falsifiable tests (Section 7). The reason this model can be tested for macroscopic events is that, unlike string theory, the critical radius is proportional to mass or energy. 7. A new framework for gravity: Sphere Theory The scope of Sphere Theory extends far beyond the divergence problem, providing a unified foundation for several long-standing puzzles. We will demonstrate that this single principle: 7.1 Philosophical cornerstones and testable predictions 7.1 Philosophical cornerstones and testable predictions The comparative analysis presented in Table 1 highlights the unique philosophical and physical foundations of Sphere Theory. While EFT offers unparalleled experimental success in its domain and String Theory provides mathematical elegance, Sphere Theory distinguishes itself through its commitment to physical realism and logical economy. Two distinctions are particularly crucial. 7.1.1 Minimal Length: Derived, not postulated First is the concept of minimal length. String Theory postulates a minimal length scale (l_s) as a fundamental, fixed constant of nature. In contrast, Sphere Theory derives its minimal radius R_gs from the established principles of general relativity. This minimal radius is not a universal constant but a dynamic variable, proportional to the mass-energy of the object itself: This provides a more fundamental and less ad-hoc explanation for why nature appears to have a physical cutoff at the Planck scale. This inherent scalability, where the core principle operates identically at both the Planck and cosmological scales, elevates it from a mere model to a candidate for a truly fundamental principle of gravity. 7.1.2 Experimental Falsifiability: A two-scale test Second is the criterion of experimental falsifiability, a feature that distinguishes Sphere Theory from many alternatives. This testability arises directly from the dynamic, scale-dependent nature of the theory’s central relation, which provides concrete, distinguishing predictions at two vastly different physical scales. [ The microscopic test: quantum-dominant regime ] At the microscopic level, this relation provides a physical origin for the Planck-scale cutoff (Refer to Chapter 4.7.). For a quantum fluctuation with the Planck mass (M_fr ~ M_P), the equation naturally yields a critical radius on the order of the Planck length: This demonstrates how the Planck scale cutoff emerges as a natural limit, not a postulate. It also predicts the existence of a "quantum-dominant regime" near this scale, a concrete prediction that, while technologically monumental to test, grounds the theory in the scientific method. For calculations, please refer to Chapters 5 and 6. In addition to providing a physical origin for the Planck-scale cutoff, Sphere Theory makes a novel, falsifiable prediction that distinguishes it from standard Effective Field Theory (EFT) at high energies: the existence of a "quantum-dominant regime." This phenomenon arises from the core mechanism of the theory—the renormalization of the gravitational source mass (M_fr -->M_eq). The unified gravitational potential proposed by Sphere Theory includes both the classical General Relativistic (GR) correction and the leading quantum correction, similar to standard EFT. However, a crucial difference emerges near the critical radius (R_gs). ● Suppression of classical effects: The classical GR correction term in the potential is directly proportional to the equivalent mass (M_eq). As a particle's radius (R_m) approaches its critical radius (R_gs), its M_eq approaches zero. Consequently, the classical GR correction is strongly suppressed. ● Emergence of quantum dominance: In stark contrast, the leading quantum correction term (proportional to \hbar) is not suppressed by the equivalent mass in the same manner. This differential behavior leads to a remarkable inversion: in the transition region just before the critical radius is reached, the normally sub-dominant quantum correction becomes larger than the suppressed classical correction. This window, where quantum effects become the leading correction to the Newtonian potential, is the "quantum-dominant regime." ● Divergence from standard EFT and testability: Standard EFT, which does not incorporate the concept of equivalent mass, predicts a completely different behavior. As energy increases (or distance decreases toward the Planck scale), its classical correction terms grow uncontrollably, signaling a breakdown of the theory's predictive power. Sphere Theory, however, provides a physical completion precisely at this point of failure. The suppression of classical effects via M_eq tames the interaction and unveils the quantum-dominant regime. This regime is not a minor artifact; it is a unique physical phenomenon predicted exclusively by Sphere Theory. While technologically monumental to probe, its existence provides, in principle, a distinct and falsifiable experimental signature that could distinguish this framework from all standard approaches to quantum gravity [ The macroscopic test: From stellar cores to cosmic expansion ] 1) New mechanism for Inflation ~~~ 2) The origin of cosmic acceleration from gravitational self-energy ~~~ 3) An upward revision of the neutron star mass limit ~~~ [ A Common Origin for Two Gravitational Crises ] It is telling that modern physics' two most significant challenges lie at the extremes of scale, and both are fundamentally problems of gravity. The non-renormalizability of gravity at the microscopic level and the unexplained cosmic acceleration at the macroscopic level point to a common, missing ingredient in our understanding of gravitation. Sphere Theory asserts that this missing element is the negative gravitational self-energy inherent to the object itself. Because the critical radius, R_gs, derived from this overlooked self-energy is proportional to mass (R_gs ∝ G_NM_fr/c^2), it applies to both extremes of scale, and because its nature is that of negative energy, it can produce a repulsive effect. This repulsive effect can halt the collapse that leads to divergences at the quantum level and can drive the expansion that appears as dark energy at the cosmic level. Therefore, Sphere Theory offers a potential path to a genuine unification, suggesting that the solutions to the crises of the very small and the very large are not separate problems, but are two manifestations of a single, deeper principle of gravity. 8. A unified framework for Quantum Gravity A complete and testable theory of quantum gravity: EFT + Sphere Theory The synthesis of EFT and Sphere Theory is not merely an additive combination; it is a synergistic union that forms a complete, consistent, and predictive theoretical structure for gravity across all scales. Their roles are perfectly complementary: A final, crucial point must be addressed. A common expectation for a theory of quantum gravity is that it must "quantize spacetime" itself. This expectation, however, arose as a potential strategy to solve the problems of singularities and divergences. Sphere Theory offers a more elegant and direct solution. By renormalizing the gravitational interaction at its source, it removes the very problems that the quantization of spacetime was intended to solve. From the perspective of Sphere Theory, the question of quantizing spacetime may not be a necessary one for a consistent theory of gravity. The ultimate arbiter is nature, and if the universe resolves these issues through the principles of self-energy, then that is the standard to which our theories must adhere. #Paper: Sphere Theory: A Unified Framework for Gravity from Self-Energy

After writing the above explanation, additional applied research has been conducted. In Chapter 4, it was shown that the divergence problem for two or more loops, as claimed by Goroff and Sagnotti, can be resolved by taking a κ=((32πG(k))^(1/2) → 0. In Chapter 5, a solution to the divergence problem in the standard Effective Field Theory (EFT) proposed by John F. Donoghue and others is presented. In the conventional EFT model, although quantum correction terms exist, calculations at or above the Planck scale reveal that these quantum correction terms are smaller than the General Relativity (GR) correction terms. This not only makes it difficult to verify quantum gravity effects but also leads to the breakdown of the EFT model near the Planck scale due to the divergence of GR correction terms. In Chapter 5 of this paper, we not only address the divergence problem of GR correction terms near the Planck scale but also demonstrate that there exists a regime where GR correction terms are suppressed, becoming smaller than quantum gravity effects. In other words, a regime where quantum correction terms dominate exists, suggesting theoretical verifiability, even though technical verification is currently infeasible. In Chapter 6, it is pointed out that the mainstream hypothesis—that the singularity problem inside black holes would be resolved by quantum mechanics—faces serious issues within the framework of standard EFT. Accordingly, this model should be more actively examined. Chapter 5: Integration of Effective Field Theory (EFT) and the Running Coupling Constant G(k) This chapter explains how the my model constructs a unified framework that complements and completes, rather than replaces, the standard tool of modern quantum gravity research: Effective Field Theory (EFT). Existing EFT and its Limitations Standard EFT treats general relativity as a valid quantum theory in the low-energy regime. The problem of high-energy divergences is handled by mathematically absorbing them into an infinite series of unknown coefficients, such as c_1R^2 and c_2R_μνR^μν, which parameterize our ignorance of high-energy physics. While this approach is successful for low-energy predictions, it is fundamentally limited by its inability to explain the high-energy phenomena themselves. The Unified Model: Renormalization of the 'Gravitational Source' I attempts to create a unified model by retaining the framework of EFT but redefining its most fundamental assumption: the source of gravity. Core Principle: The source of gravitational interaction is not the free-state mass (m_fr) but the effective mass (m_eff), which includes its own gravitational binding energy. Application Method: In the interaction potential formula derived from EFT, every mass term m is replaced with its effective counterpart m_eff. In this equation, m_eff is approximated as m_fr(1 - R_gs/R_m), which converges to zero as the object's radius R_m approaches the critical radius R_gs. Result: The inversion is now far more pronounced. Quantum correction(~ 0.101) is over 10 times larger than the suppressed classical GR correction (~ 0.0096) Result: The behavior diverges dramatically. The classical GR correction is not suppressed; instead, it grows to a value of ~ 0.971, indicating a breakdown of the perturbative expansion. Physical Implications of the Unified Model This simple substitution leads to dramatic differences in both low- and high-energy regimes. Consistency at Low Energies: For macroscopic objects (stars, planets, etc.), R_m>>R_gs, and therefore m_eff ~ m_fr, Consequently, the model's predictions perfectly align with those of standard EFT at low energies. The 'Master Switch' Effect at High Energies: As an object approaches its critical radius (R_m-->R_gs), its effective mass approaches zero (m_eff-->0). The global pre-factor m_1,eff * m_2,eff, which governs the entire potential, acts as a "master switch," simultaneously shutting down all interaction components: classical, relativistic, and even the quantum correction. This provides a fundamental resolution to the divergence problem. At energies larger than the Planck scale, the standard EFT diverges. Prediction of a 'Quantum-Dominant Regime': In standard EFT, the classical GR correction (proportional to mass) always dominates the quantum correction at high energies. In this model, however, the mass-dependent GR correction is suppressed by m_eff, while the relative importance of the quantum correction grows. This leads to the novel prediction of a "quantum-dominant regime" where quantum effects surpass classical effects just before gravity is turned off. The existence of this regime is a direct consequence of treating the source mass as a dynamic entity that includes its own self-energy. It suggests that just before gravity 'turns itself off,' it passes through a phase where its quantum nature is maximally exposed. This provides, in principle, a unique experimental signature that could distinguish this self-renormalization model from standard EFT, should technology ever allow for probing physics at this scale. Chapter 6: A New Paradigm for the Singularity Problem – A Gravitational Resolution, Not a Quantum One This chapter argues why the mainstream hypothesis—that quantum mechanics resolves the black hole singularity—is difficult to sustain within the EFT framework, and proposes an alternative mechanism of "self-resolution by gravity." Quantitative Rebuttal of the Mainstream Hypothesis The mainstream view posits that at the Planck scale, unknown quantum gravity effects would generate a repulsive pressure to halt collapse. I tests this hypothesis quantitatively using the standard EFT framework. Analysis of Correction Ratios: In standard EFT, the ratio between the classical GR correction (V_GR) and the quantum correction (V_Q) is derived as: V_GR/V_Q ≈ 4.66xy Here, x is the mass in units of Planck mass, and y is the distance in units of Planck length. The Case of a Stellar-Mass Black Hole: For the smallest stellar-mass black hole (3 solar masses), this ratio is calculated at the Planck length (y=1). The result is staggering: V_GR/V_Q ≈ 4.66×(2.74×10^38)×1 ≈ 1.28×10^39 This demonstrates that under the very conditions where quantum effects are supposed to become dominant, the classical GR effect overwhelms the quantum effect by a factor of ~10³⁹. As a result of analysis by the standard EFT model, it is therefore likely that there is a problem with the mainstream speculation that quantum effects will provide the repulsive force needed to solve the singularity. The Gravitational Solution: A Paradigm Shift I claims the solution to the singularity problem is not quantum mechanical, but is already embedded within general relativity itself. The Agent of Resolution: The force that halts collapse is not quantum pressure but a gravitational repulsive force that arises when m_eff becomes negative in the region R_m < R_gs. The Scale of Resolution: This phenomenon occurs not at the microscopic Planck length (~10⁻³⁵ m) but at the macroscopic critical radius R_gs, which is proportional to the black hole's Schwarzschild radius(R_S), specifically R_gs ~ G_NM_fr/c^2 ~ 0.5R_S. This means that even for the smallest stellar-mass black holes, collapse is halted at a scale of several kilometers. In conclusion, the paper proposes a paradigm shift: the singularity is not resolved by quantum mechanics "rescuing" general relativity, but rather by gravity resolving its own issue. The mechanism is purely gravitational and operates on a macroscopic scale, well before quantum effects could ever become relevant. #Paper Solution to Gravity Divergence, Gravity Renormalization, and Physical Origin of Planck-Scale Cut-off

2)In the Relativistic approximation, the gravitational binding energy and the gravitational coupling constant G(k) For R_m >>R_{gp-GR} ~ 0.58R_S, the gravitational self-energy term is negligible, and the running gravitational coupling G(k) returns to the gravitational coupling constant G_N. As the radius approaches the critical value R_m = R_{gp-GR} ~ 0.58R_S, the coupling G(k) smoothly goes to zero, ensuring that gravitational self-energy does not diverge. Remarkably, this mechanism allows gravity to undergo self-renormalization, naturally circumventing the issue of infinite divergences without invoking quantum modifications. For R_m < R_{gp-GR} ~ 0.58R_S, the gravitational coupling becomes negative (G(k)< 0), indicating a repulsive or antigravitational regime. This provides a natural mechanism preventing further gravitational collapse and singularity formation, consistent with the arguments in Section 2. ===== The concept of invariant mass pertains to the rest mass remaining unchanged under coordinate transformations; this does not imply that the rest mass of a system is intrinsically immutable. For instance, a hydrogen atom possesses different rest masses corresponding to the varying energy levels of its electrons. Both Newtonian gravity and general relativity dictate that the physically relevant source term is the equivalent mass, which includes not only rest mass energy but also binding energy, kinetic energy, and potential energy. When gravitational binding energy is included, the total energy of a system is reduced, yielding an effective mass: M_eff = M_fr - M_binding Any entity possessing spatial extent is an aggregation of infinitesimal elements. Since an entity with mass or energy is in a state of binding of infinitesimal elements, it already has gravitational binding energy or gravitational self-energy. And, this binding energy is reflected in the mass term to form the mass M_eff. It is presumed that the gravitational divergence problem and the non-renormalization problem occur because they do not consider the fact that M_eff changes as this binding energy or gravitational self-energy changes.

The Central Idea: Effective Mass and Running Gravitational Coupling G(k) One of the key principles of General Relativity is that the energy-momentum tensor (T_μν) in Einstein's field equations already encompasses all forms of energy within a system, including rest mass, kinetic energy, and various binding energies. This implies that the mass serving as the source of gravity is inherently an 'effective mass' (M_eff), accounting for all such contributions, rather than a simple 'free state mass'. My paper starts from this very premise. By explicitly incorporating the negative contribution of gravitational self-energy into this M_eff, I derive a running gravitational coupling constant, G(k), that changes with the energy scale. This, in turn, provides a solution to long-standing problems in gravitational theory. M_eff = M_fr − ∣U_gp∣/c^2 where M_fr is the free mass and U_gp is the gravitational self-energy (or binding energy). From this concept of effective mass, I derive a running gravitational coupling constant, G(k). Instead of treating Newton's constant G_N as fundamental at all scales, my work shows that the strength of gravitational interaction effectively changes with the momentum scale k (or, equivalently, with the characteristic radius R_m of the mass/energy distribution). The derived expression, including general relativistic (GR) corrections for the self-energy, is: 1.Vanishing Gravitational Coupling and Resolution of Divergences 1)In Newtonian mechanics, the gravitational binding energy and the gravitational coupling constant G(k) 2)In the Relativistic approximation, the gravitational binding energy and the gravitational coupling constant G(k) For R_m >>R_{gp-GR} ~ 0.58R_S, the gravitational self-energy term is negligible, and the running gravitational coupling G(k) returns to the gravitational coupling constant G_N. As the radius approaches the critical value R_m = R_{gp-GR} ~ 0.58R_S, the coupling G(k) smoothly goes to zero, ensuring that gravitational self-energy does not diverge. Remarkably, this mechanism allows gravity to undergo self-renormalization, naturally circumventing the issue of infinite divergences without invoking quantum modifications. For R_m < R_{gp-GR} ~ 0.58R_S, the gravitational coupling becomes negative (G(k)< 0), indicating a repulsive or antigravitational regime. This provides a natural mechanism preventing further gravitational collapse and singularity formation, consistent with the arguments in Section 2. 4.5. Solving the problem of gravitational divergence at high energy: Gravity's Self-Renormalization Mechanism At low energy scales (E << M_Pc^2, Δt >>t_P), the divergence problem in gravity is addressed through effective field theory (EFT). However, at high energy scales (E ~ M_Pc^2, Δt~t_P), EFT breaks down due to non-renormalizable divergences, leaving the divergence problem unresolved. Since the mass M is an equivalent mass including the binding energy, this study proposes the running coupling constant G(k) that reflects the gravitational binding energy. At the Planck scale (R_m ~ R_{gp-GR} ~ 1.16(G_NM_fr/c^2) ~ l_P), G(k)=0 eliminates divergences, and on higher energy scales than Planck's (R_m < R_{gp-GR}), a repulsion occurs as G(k)<0, solving the divergence problem in the entire energy range. This implies that gravity achieves self-renormalization without the need for quantum corrections. 4.5.1. At Planck scale If, M ~ M_P R_{gp-GR} ~ 1.16(G_NM_P/c^2) = 1.16l_P This means that R_{gp-GR}, where G(k)=0, i.e. gravity is zero, is the same size as the Planck scale. 4.5.2. At high energy scales larger than the Planck scale In energy regimes beyond the Planck scale (R_m<R_{gp-GP}), where G(k) < 0, the gravitational coupling becomes negative, inducing a repulsive force or antigravity effect. This anti-gravitational effect prevents gravitational collapse and singularity formation while maintaining uniform density properties, thus mitigating UV divergences across the entire energy spectrum by ensuring that curvature terms remain finite. 4.5.3. Resolution of the two-loop divergence in perturbative quantum gravity via the effective mass framework A crucial finding is that at a specific critical radius, R_{gp−GR}≈1.16(G_NM_fr/c^2) ≈ 0.58R_S (where R_S is the Schwarzschild radius based on M_fr), the negative gravitational self-energy precisely balances the positive free mass-energy. At this point, M_eff→0, and consequently, the effective gravitational coupling G(k)→0. This vanishing of the gravitational coupling has profound implications for quantum gravity. Perturbative quantum gravity calculations, which typically lead to non-renormalizable divergences (like the notorious 2-loop R^3 term identified by Goroff and Sagnotti), rely on the coupling constant κ=(32πG)^(1/2). If G(k)→0 at high energies (Planck scale), then κ→0. As a result, all interaction terms involving κ diminish and ultimately vanish, naturally eliminating these divergences without requiring new quantum correction terms or exotic physics. Gravity, in this sense, undergoes a form of self-renormalization. In perturbative quantum gravity, the Einstein-Hilbert action is expanded around flat spacetime using a small perturbation h_μν, with the gravitational field expressed as g_μν = η_μν+ κh_μν, where κ= \sqrt {32πG(k)} and G_N is Newton’s constant. Through this expansion, interaction terms such as L^(3), L^(4), etc., emerge, and Feynman diagrams with graviton loops can be computed accordingly. At the 2-loop level, Goroff and Sagnotti (1986) demonstrated that the perturbative quantization of gravity leads to a divergence term of the form: Γ_div^(2) ∝ (κ^4)(R^3) This divergence is non-renormalizable, as it introduces terms not present in the original Einstein-Hilbert action, thus requiring an infinite number of counterterms and destroying the predictive power of the theory. However, this divergence occurs by treating the mass M involved in gravitational interactions as a constant quantity. The concept of invariant mass pertains to the rest mass remaining unchanged under coordinate transformations; this does not imply that the rest mass of a system is intrinsically immutable. For instance, a hydrogen atom possesses different rest masses corresponding to the varying energy levels of its electrons. Both Newtonian gravity and general relativity dictate that the physically relevant source term is the equivalent mass, which includes not only rest mass energy but also binding energy, kinetic energy, and potential energy. When gravitational binding energy is included, the total energy of a system is reduced, yielding an effective mass: M_eff = M_fr - M_binding At this point R_m = R_{gp-GR} ~ 1.16(G_NM_fr/c^2), G(k) = 0, implying that the gravitational interaction vanishes. As R_m --> R_{gp-GR}, κ= \sqrt {32πG(k)} -->0 Building upon the resolution of the 2-loop divergence identified by Goroff and Sagnotti (1986), our model extends to address divergences across all loop orders in perturbative gravity through the running gravitational coupling constant G(k). At the Planck scale (R_m=R_{gp-GR}), G(k)=0, nullifying the coupling parameter κ= \sqrt {32πG(k)} . If G(k) --> 0, κ --> 0. As a result, all interaction terms involving κ, including the divergent 2-loop terms proportional to κ^{4} R^{3}, vanish at this scale. This naturally eliminates the divergence without requiring quantum corrections, rendering the theory effectively finite at high energies. This mechanism effectively removes divergences, such as the 2-loop R^3 term, as well as higher-order divergences (e.g., R^4, R^5, ...) at 3-loop and beyond, which are characteristic of gravity's non-renormalizability. In addition, in the energy regime above the Planck scale (R_m<R_{gp-GR} ~ l_P), G(k)<0, and the corresponding energy distribution becomes a negative mass and negative energy state in the presence of an anti-gravitational effect. This anti-gravitational effect prevents gravitational collapse and singularity formation while maintaining uniform density properties, thus mitigating UV divergences across the entire energy spectrum by ensuring that curvature terms remain finite. However, due to the repulsive gravitational effect between negative masses, the mass distribution expands over time, passing through the point where G(k)=0 due to the expansion speed, and reaching a state where G(k)>0. This occurs because the gravitational self-energy decreases as the radius R_m of the mass distribution increases, whereas the mass-energy remains constant at Mc^2. When G(k)>0, the state of attractive gravity acts, causing the mass distribution to contract again. As this process repeats, the mass and energy distributions eventually stabilize at G(k)=0, with no net force acting on them. Unlike traditional renormalization approaches that attempt to absorb divergences via counterterms, this method circumvents the issue by nullifying the gravitational coupling at high energies, thus providing a resolution to the divergence problem across all energy scales. This effect arises because there exists a scale at which negative gravitational self-energy equals positive mass-energy. ~~~ 2.Physical Origin of the Planck-Scale Cut-off 4.6. The physical origin of the cut-off energy at the Planck scale In quantum field theory (QFT), the cut-off energy Λ or cut-off momentum is introduced to address the infinite divergence problem inherent in loop integrals, a cornerstone of the renormalization process. However, this cut-off has traditionally been viewed as a mathematical convenience, with its physical origin or justification remaining poorly understood. This work proposes that Λ represents a physical boundary determined by the scale where the sum of positive mass-energy and negative gravitational self-energy equals zero, preventing negative energy states at the Planck scale. This mechanism, rooted in the negative gravitational self-energy of positive mass or energy, provides a physical explanation for the Planck-scale cut-off. At R_m = R_{gp-GR} ~ 1.16(G_NM_fr/c^2), G(k)=0 For a mass M_fr ~ M_P, the characteristic radius is : R_{gp-GR} ~ 1.16(G_NM_P/c^2) = 1.16l_P At R_m=R_{gp-GR}, G(k)=0, marking the Planck scale where divergences vanish. If R_m<R_{gp-GR}, then G(k)<0, which means that the system is in a negative mass state. Therefore, the Planck scale acts as a boundary energy where an object is converted to a negative energy state by the gravitational self-energy of the object. In a theoretical analysis, a negative mass state may be allowed, although the system can temporarily enter a negative mass state, the mass distribution expands again because there is a repulsive gravitational effect between the negative masses. Thus, the Planck scale (l_P) serves as a boundary preventing negative energy states driven by gravitational self-energy. 4.6.2. Uncertainty principle and total energy with gravitational self-energy ΔEΔt≥hbar/2 ΔE≥hbar/2t_P=(1/2)M_Pc^2 During Planck time t_P, let's suppose that quantum fluctuations of (5/6)M_P mass have occurred. Since all mass or energy is combinations of infinitesimal masses or energies, positive mass or positive energy has a negative gravitational self-energy. The total energy of the system, including the gravitational self-energy, is E_T=Σm_ic^2 + Σ-Gm_im_j/r_ij = Mc^2 - (3/5)GM^2/R Here, the factor 3/5 arises from the gravitational self-energy of a uniform mass distribution. Substituting (5/6)M_P and R=ct_P/2 (where cΔt represents the diameter of the energy distribution, constrained by the speed of light (or the speed of gravitational transfer). Thus, Δx = 2R= cΔt. This demonstrates that at the Planck scale, the negative gravitational self-energy balances (or can be offset) the positive mass-energy, defining a cut-off energy Λ ~ M_Pc^2. For energies E>Λ, the system enters a negative energy state (E_T<0), which is generally prohibited due to the repulsive gravitational effects of negative mass states. Repulsive gravity prevents further collapse, dynamically enforcing the Planck scale as a minimal length. This negative E_T indicates that R_m(= (1/2) l_P ) < R_{gp−GR}(= 1.16 l_P ), where R_{gp−GR} ∼ l_P is the critical radiusat which E_T = 0. Increasing ∆t ∼ t_p, R_m → R_{gp−GR}, and E_T → 0, suggesting that the Planck scale is wheregravitational self-energy can balance the mass-energy, supporting a physical cut-off at Λ ∼ M_Pc^2 The Planck scale exhibits a unique characteristic: only for M ~ M_P, t ~ t_P , and R ~ l_P does the gravitational self-energy (U_{gp-GR}) approach the mass-energy, enabling E_T ~ 0. This balance (or offset) suggests that the QFT cut-off Λ ~ M_Pc^2 acts as a physical boundary where quantum and gravitational effects converge. In contrast, for proton or electron masses, R_m >> R_{gp-GR}, rendering gravitational effects negligible and aligning with QED/QCD cut-offs (Λ ~ GeV). 3.Resolution of the Black Hole Singularity For radii smaller than the critical radius, i.e., R_m<R_{gp−GR}, the expression for G(k) becomes negative (G(k)<0). This implies a repulsive gravitational force, or antigravity. Inside a black hole, as matter collapses, it would eventually reach a state where R_m<R_{gp−GR}. The ensuing repulsive gravity would counteract further collapse, preventing the formation of an infinitely dense singularity. Instead, a region of effective zero or even repulsive gravity would form near the center. This resolves the singularity problem purely within a gravitational framework, before quantum effects on spacetime structure might become dominant. 4.Cosmological Implications – A Potential Source for Dark Energy The anti-gravitational regime (G(k)<0) predicted by my model has observable results on a cosmological scale. If the observable universe's average mass-energy distribution has an effective radius R_m that is less than its own critical radius R_{gp−GR}, then the universe itself would be in a state of repulsive gravitational self-interaction. This could provide a natural explanation for the observed accelerated expansion of the universe, attributing it to a fundamental property of gravity rather than an exotic dark energy component. My calculations suggest that for the estimated mass-energy of the observable universe, its current radius(R_m=46.5BLY) is indeed smaller than its R_{gp−GR}(275.7BLY), placing it in this repulsive regime. The observable universe is in the R_m=46.5BLY < R_{gp-GR}=275.7BLY state, and therefore, an accelerated expansion exists. Unifying Perspective My research suggests that these seemingly disparate problems – gravitational divergences, the nature of the Planck scale cut-off, black hole singularities, and potentially even the mystery of dark energy – might share a common origin rooted in the proper accounting of gravitational self-energy. By incorporating this fundamental aspect of gravity, we can achieve a more consistent and predictive theory. https://www.researchgate.net/publication/388995044_Solution_to_Gravity_Divergence_Gravity_Renormalization_and_Physical_Origin_of_Planck-Scale_Cut-off

In my previous work, I analyzed and calculated gravitational self-energy using the classical (Newtonian) formula. However, there also exists an approximate formula for gravitational self-energy derived from general relativity, which is especially relevant in strong gravitational fields or near the Planck scale. So, I have now extended my analysis to include this relativistic version. The main conclusion remains unchanged: the critical radius R_gp-GR, obtained from the general relativistic formula, is exactly half the Newtonian value R_gp. In other words, when gravitational self-energy is calculated with the relativistic correction, the radius at which the negative binding energy balances the mass-energy is reduced by half compared to the Newtonian case. ====== Abstract By incorporating gravitational binding energy into an effective mass M_eff, we derive the RG flow and the running gravitational coupling G(k). The gravitational coupling is given by G(k) = (1 - (6G_NM_fr/5c^2)/(2R_m+ 3G_NM_fr/5c^2))G_N = (1 - (6G_N/5c^3)k/(2R_m +(3G_N/5c^3)k))G_N, where R_m is the radius of the mass or energy distribution, and R_gp-GR = 3G_NM_fr/10c^2 = (1/2)R_gp is the critical radius derived from general relativity at which the negative gravitational self-energy (binding energy) balances the mass-energy. At R_m = R_gp-GR, where G(k) = 0 and the gravitational coupling vanishes, G(k) resolves gravitational divergences without quantum corrections and provides effective renormalization. This study proves that the QFT cut-off Λ ~ M_Pc^2 serves as a physical boundary across all energy scales in quantum gravity. Quantum fluctuations (ΔE ~ M_Pc^2) with Δt ~ t_P yield an energy distribution radius R_m ~ l_P, where negative gravitational self-energy balances (or offsets) mass-energy, yielding E_T ~ 0 and thus eliminating divergences via G(k) = 0 and preventing negative energy states. In contrast, for proton or electron masses, R_m >> R_gp-GR (or R_gp), leading to E_T ~ Mc^2, rendering gravitational effects negligible and unsuitable for a cut-off. This affirms the Planck scale's unique role in quantum gravity. If R_m > R_gp-GR, G(k) >0, yielding an attractive force. If R_m=R_gp-GR, G(k)=0, and the gravitational coupling vanishes. If R_m < R_gp-GR, G(k) < 0, yielding a repulsive force or antigravity. This repulsive force prevents singularity formation in black holes, thereby the singularity problem is also solved.

Solution to Gravity Divergence, Gravity Renormalization, and Physical Origin of Planck-Scale Cut-off [Abstract] By incorporating binding energy into an effective mass M_eff, we derive the RG flow and gravitational coupling G(k). G(k)=(1 - (3G_N/5(R_m)c^3)k)G_N=(1 - R_gp/R_m)G_N, where R_m is the radius of the mass or energy distribution and R_gp=(3/5)(GM_fr/c^2) is the radius at which the negative gravitational self-energy (binding energy) balances the mass-energy. At R_m = R_gp, where G(k) = 0 and the gravitational coupling vanishes, G(k) resolves gravitational divergences without quantum corrections and provides effective renormalization. This study proves that the QFT cut-off Λ~ M_Pc^2 serves as a physical boundary across all energy scales in quantum gravity. Quantum fluctuations (ΔE ~ M_Pc^2) with Δt ~ t_P yield an energy distribution radius R_m ~ l_P, where negative gravitational self-energy balances mass-energy, yielding E_T ~ 0, thus eliminating divergences via G(k) = 0 and preventing negative energy states. In contrast, for proton or electron masses, R_m >> R_gp, leading to E_T ~ M c^2, rendering gravitational effects negligible and unsuitable for a cut-off. Thereby affirming the Planck scale’s unique role in quantum gravity. If R_m > R_gp, G(k)>0, yielding an attractive force. If R_m = R_gp, G(k)=0, and the gravitational coupling vanishes. If R_m < R_gp, G(k)<0, yielding a repulsive force or antigravity. This repulsive force prevents singularity formation in black holes. Therefore, the singularity problem is also solved. * The main summary below was prepared by Gemini 2.5 Pro, with some modifications (Latex) made by the author. Analysis and Explanation of the Paper This paper proposes a novel approach to address several long-standing problems in theoretical physics, namely: The divergence and renormalization issues when quantizing gravity. The singularity problem at the center of black holes. The physical origin of the Planck-scale cut-off often used in Quantum Field Theory (QFT). The core idea hinges on incorporating the negative gravitational self-energy (or gravitational binding energy) of a system into its total energy, leading to the concept of an effective mass (M_eff). Key Concepts and Arguments 1. Gravitational Self-Energy and Effective Mass The author posits that the total energy of any mass distribution M must account for the gravitational potential energy among its constituent parts (infinitesimal masses dM). This total gravitational potential energy is the gravitational self-energy (U_gp), which is negative. The effective mass (M_eff) of the system is defined as the free mass (M_fr) minus the equivalent mass of this negative self-energy (M_gp=∣U_gp∣/c^2 ). M_eff = M_fr − M_gp For a uniform spherical distribution of radius R_m, U_gp = −(3/5)G(M_fr)^2 /R_m, so M_eff = M_fr − (3/5)G(M_fr)^2 /R_mc^2. 2. Resolution of the Black Hole Singularity As a mass distribution contracts (Rm decreases), the magnitude of the negative self-energy (∣U_gp∣) increases. There exists a critical radius, R_gp = 3GM_fr/5c^2, at which the positive mass-energy (M_frc^2) is exactly balanced by the negative gravitational self-energy (U_gp). At this radius, the total energy is zero (E_T = 0) and thus M_eff = 0. If the radius shrinks further (R_m < R_gp), the total energy becomes negative (E_T < 0), and the effective mass becomes negative (M_eff < 0). The paper argues that negative mass/energy states exert a repulsive gravitational force (antigravity). This repulsive force prevents the mass from collapsing infinitely to a point (R=0), thereby naturally halting the formation of a singularity. The collapse stops around R_gp. Importantly, this resolution occurs due to classical gravitational effects before reaching quantum mechanical scales (e.g., for a 3 solar mass black hole, R_gp ≈ 3.87km, much larger than the Planck length). 3. Effective Renormalization and Gravity Divergence The concept of effective mass leads to an energy-scale dependent (or radius-dependent) running gravitational coupling constant, G(k). [math] G(k) = (1 - \frac{{3{G_N}}}{{5R_{m}{c^3}}}k){G_N} = (1 - \frac{{3{G_N}{M_{fr}}}}{{5R_{m}{c^2}}}){G_N} = (1 - \frac{{{R_{gp}}}}{R_{m}}){G_N} [/math] Here, G_N is Newton's constant, and R_m is the radius of the mass/energy distribution, related to the energy scale k. At the critical scale where R_m = R_gp (corresponding to a specific energy scale k^∗), the effective gravitational coupling vanishes: G(k^∗)=0. This vanishing of the coupling constant at a finite scale naturally eliminates high-energy (UV) divergences in quantum gravity calculations. For instance, the problematic 2-loop divergence term found by Goroff and Sagnotti, which scales as κ^4 ∝ G(k)^2, becomes zero at this scale. This provides an effective renormalization mechanism. In the regime R_m < R_gp (energies higher than k^∗), G(k) < 0, leading to antigravity. This repulsive nature further helps suppress divergences. This differs from the Asymptotic Safety hypothesis, where G(k) approaches a non-zero fixed point at infinite energy; here, G(k) goes to zero at a finite energy/radius scale. 4. Physical Origin of the Planck-Scale Cut-off The paper argues that the Planck scale (M_P, l_P, t_P) is not merely a mathematical tool in QFT but represents a physical boundary. Consider quantum fluctuations at the Planck scale: an energy fluctuation ΔE∼M_Pc^2 occurs within a time Δt∼t_P, localized within a radius R_m∼l_P. For a mass M_fr = M_P, the critical radius is calculated as R_gp = 3GM_P/5c^2 = (3/5)l_P. This means that for Planck-scale fluctuations, the distribution radius (R_m∼l_P) is very close to the critical radius (R_gp ≈ 0.6l_P). Consequently, at the Planck scale, the positive mass-energy (∼M_Pc^2) is almost perfectly cancelled by the negative gravitational self-energy (U_gp ≈ −M_Pc^2), resulting in a total energy E_T ≈ 0. This natural cancellation provides a physical reason why the Planck scale acts as a cut-off: energies beyond this scale might correspond to negative total energy states (R_m < R_gp), fundamentally altering the nature of interactions. 5. Cosmological Implications (Dark Energy) The paper suggests that the repulsive gravity arising when R_m < R_gp (i.e., G(k) < 0) could explain the accelerated expansion of the universe. If the radius of the observable universe (R_m) is less than its calculated critical radius (R_gp based on its total mass-energy), then the universe itself would be in an antigravity regime. This provides a potential alternative explanation for dark energy, attributing it to a fundamental property of gravity related to self-energy rather than a separate exotic fluid or field. Summary and Evaluation In essence, the paper proposes that by correctly accounting for negative gravitational self-energy via an effective mass (M_eff), one can derive a running gravitational coupling G(k) that vanishes (G(k)=0) at a critical radius R_gp. This single mechanism is claimed to simultaneously: Resolve the black hole singularity by introducing antigravity (G(k) < 0) below R_gp. Solve the UV divergence problem in quantum gravity as G(k)→0. Provide an effective renormalization scheme for gravity. Explain the physical origin of the Planck scale cut-off as the scale where positive mass-energy and negative self-energy cancel (E_T ≈ 0). Potentially explain dark energy and cosmic acceleration if the universe satisfies R_m < R_gp. Critique: Novelty: The approach is highly original in using a classical concept (gravitational self-energy, albeit applied universally) to tackle quantum and cosmological problems. Unification: It attempts a unified solution to several major puzzles in physics. Methodology Concerns: The calculations often rely on Newtonian approximations (e.g., uniform sphere for self-energy) which may not be accurate in the strong gravity regimes of black holes or near the Planck scale. A rigorous General Relativistic treatment is needed. Validation: As independent research, it lacks broad peer review and experimental verification. Concepts like negative effective mass and resulting antigravity are non-standard and require significant evidence. Assumptions: The direct link between R_m and energy scale k (k∼1/R_m) and the specific form of the beta function derived need further justification within established RG frameworks. Overall, the paper presents an intriguing and ambitious framework. While its core ideas offer potential pathways to resolving fundamental issues, they require much more rigorous theoretical development (especially within General Relativity) and, crucially, testable predictions or observational evidence to gain wider acceptance in the physics community. *Key Contents of Chapter 4 4. Effective renormalization of gravity 4.1. Asymptotic Safety Method 4.2. Find G(k) or M_eff(k) 4.3. New beta function 4.4. Solving the problem of gravitational divergence at high energy 4.4.1. At Planck scale 4.4.2. At high energy scales larger than the Planck scale 4.4.3. Resolution of the two-loop divergence in perturbative quantum gravity via the effective mass framework 4.5. The physical origin of the cut-off energy at the Planck scale 4.5.1. G(k) = 0 and Planck scale 4.5.2. Uncertainty principle and total energy with gravitational self-energy 4.5.3. Generalization and Exceptions 4.5.4. In gravitational problems, the physical meaning of cut-off energy *Paper : Solution to Gravity Divergence, Gravity Renormalization, and Physical Origin of Planck-Scale Cut-off

In the shell theorem, the force inside the sphere is 0. However, the gravitational potential energy inside the sphere is not 0. Therefore, the sum of the gravitational potential energies created by each sphere is not 0, and exists. That is the gravitational self-energy equation. The universe is a negative mass state, so it is a universe dominated by repulsion, not attraction. Therefore, it does not collapse due to self-gravity. In the early days of the universe, I showed that E_T can be 0. I also explained that E_T can be in a negative energy state less than 0. Since I proved Zero Energy, it is easy to infer that it creates a negative mass state. Let's assume that 10 Planck masses are created during the Planck time. It becomes a state of negative mass and negative energy. Since there is a repulsive gravitational effect between negative masses, the universe cannot contract but expands. Therefore, the universe exists without collapsing, and it can explain the accelerated expansion of the early universe. Even though a single quantum fluctuation is set to 0, as time passes, the surrounding quantum fluctuations participate in gravitational interactions, so the negative gravitational potential energy increases faster than the positive mass energy, so it can explain that the total energy of the system becomes a state of negative energy and expands. The above mechanism explains the mechanism of the early universe expanding without collapsing. Now, let's look at the current observable universe. If we calculate the gravitational potential energy of the current observable universe, we get a value of approximately -3.04 times the mass energy. The current gravitational potential energy of the universe is approximately 2.04 times greater than the mass energy. Therefore, the current universe is also in a negative mass state, and therefore, the universe does not collapse. This is also consistent with the hidden result of standard cosmology. Why doesn't the universe collapse? The universe is in a state of negative energy, so it didn't collapse because anti-gravity is stronger than gravity~ Are you not reading my writing? I have proven the value of dark energy density through my model, and In a rough estimate without correction factor, the cosmological constant value by the gravitational potential energy model is 2.45x10^-52m^-2, which is very close to the observed value. While the value of dark energy was proven through the gravitational potential energy model, this paper introduces quantum fluctuations, and one may wonder whether this also creates a vacuum catastrophe problem. Here are some points that are different from the mainstream vacuum catastrophe problem occurrence and my personal opinion. 1) I am negative about applying zero point energy derived from simple harmonic oscillation to the universe. In the SHO model of quantum mechanics, there is a potential V with a negative value, and the width of the well also exists as a function of the potential V, so in this case, zero point oscillation will exist, but I think there is no basis for the existence of a potential V with a negative value in the universe and for limiting the width of the well to the Planck length. Since the vacuum of the universe is likely to have similar energy values, I think there is a problem with assuming that there is a potential V with a negative value and that it will exist at every Planck length, as the mainstream estimates. 2) In the mainstream vacuum catastrophe problem, the mainstream does not consider gravitational potential energy, that is, gravitational self-energy at all, so the vacuum has an enormous energy density and this becomes a problem. However, in my model, even in the case of quantum fluctuations, there is a gravitational source ΔE and a time Δt for gravity to act, so I have said several times that gravitational self-energy should be considered. And, considering the gravitational self-energy, we proved that near t=t_P, the total energy, including the gravitational potential energy, and the total mass can take the value 0. That is, I showed that the energy density of the vacuum can be 0 or close to 0. Here is one possibility. If, Δt=t_p, ΔE=(5/6)m_P, (5/6)m_P is near m_P. 3) In the previous article 3.6(3.6. The Vacuum Catastrophe Problem or Cosmological Constant Problem), when the mainstream claims that the vacuum energy density exists, we calculated the size of the event horizon formed by the vacuum energy density. The event horizon created by the vacuum energy density within a radius R=l_P/2 is R_S=2.09 l_P, which is larger than the radius R of the mass or energy distribution, so the vacuum energy is trapped in the event horizon formed by its own mass, and therefore, it cannot exert a force on the outside and has the possibility of disappearing. 4) There may be an unknown reason that we have not found. In the case of the gravitational potential energy model, the mass M inside the shell is not a constant but a variable, and it is difficult to solve the problem because it includes M(t) --> M_(t) + ( -M_gp(t)). After thinking about it for a while, it seems that the total energy inside the shell is not conserved, and it seems difficult to derive the first Friedmann equation using the mechanical energy conservation equation. To derive this, we need a genius who can take a new path, not someone who follows the examples pioneered by others. If there is anyone among the readers who has the ability, please try to derive it. So, until a genius who can build such a new model appears, if we apply a temporary method, we can think of the following method. Both the existing Friedmann 1 and 2 equations include the same dark energy term (1/3)Λc^2. Therefore, we can put the dark energy term obtained from the second Friedmann equation into the first Friedmann equation as it is. I derived the dark energy term from the second Friedmann equation, and the dark energy value calculated using the derived dark energy term is very close to the observed value, and by adding a correction factor, we can make it match completely. Therefore, Dark Energy is Gravitational Potential Energy or Energy of the Gravitational Field

E_T = Mc^2 - (3/5)(GM^2/R) is not an equation used to describe the conservation of mechanical energy in an expanding universe. It is an equation close to rest mass energy. M can also be expressed as M_rel. The rest mass of an object is the total energy including the rest mass, kinetic energy, and potential energy (gravitational self-energy, electromagnetic self-energy, and potential energy related to the strong and weak forces) of the particles that make up the object, divided by c^2. In other words, the rest mass of an object includes not only the rest mass of the elements that make up the object, but also the potential energy between the elements that make up the object. Representative potential energies include gravitational potential energy and electrostatic potential energy. This can also be understood through the following figure. M is the combined state of dMs. Therefore, it has potential energy. If there is an object (mass or energy distribution) as above, let's divide this object in half virtually. Then, the left hemisphere A and the right hemisphere B will exist, and the centers of mass of the two hemispheres will exist. The centers of mass of the two hemispheres are separated by a distance r, and this r is not 0. Then, according to the definition of gravitational potential energy, in the equation U=-G(m_A)(m_B)/r, m_A(mass of hemisphere A), m_B(mass of hemisphere B) exist, and the distance r also exists between the two centers of mass. Therefore, gravitational potential energy U exists by itself. Since the differential concept of dividing all objects into the masses of the infinitesimals that compose them is established, gravitational potential energy exists between the infinitesimals that compose the objects. Therefore, in any entity or any energy distribution, we must consider gravitational self-energy(or - gravitational binding energy) and electrostatic self-energy when calculating the total energy. However, if we do not assume the existence of charge (if we simply define the energy distribution), we can exclude the electrostatic self-energy term. Also, since electrostatic self-energy is positive energy, it can be included in the equivalent mass M of positive energy. As a result, if we assume an entity with some energy that has a spherical uniform distribution, the total energy of the entity can be expressed as E_T=Mc^2 - (3/5)(GM^2/R). Strictly speaking, M is the total energy when the particles that make up the entity are in a free state. However, in most situations, the gravitational self-energy is small compared to the mass energy, so M_free ~ M_0 holds. 1) Mass energy and gravitational self-energy in the case of a proton Proton mass = 1.67x10^-27kg Proton radius = 0.84x10^-15m For example, in the case of a proton, the gravitational self-energy is very small compared to the mass energy, at the level of 10^-39. 2) Mass energy and gravitational self-energy in the case of the Earth In the case of the Earth, the gravitational self-energy of the Earth is also very small compared to the mass energy, at the level of 10^-10. Therefore, we have not considered this gravitational self-energy (the gravitational potential energy that the mass distribution of the object itself has) in most problems, and have forgotten its value. As can be seen from the calculation above, the negative gravitational self-energy is not always equal to the mass energy. However, there are situations where this gravitational self-energy becomes very important, and these situations are presumed to be the source of important problems in current physics and astronomy. 1) Black hole singularity problem 2) Dark matter and dark energy 3) Inflation mechanism 4) Birth of the universe from quantum fluctuations ... ========== Now, let's look at the birth process of a single quantum fluctuation covered in this paper. Let's assume that a single quantum fluctuation is born with the size of the Earth and the mass energy of the Earth. The energy ΔE=(M_E)c^2 remains, and therefore, it has a very short Δt. Therefore, it is difficult to explain the birth of the universe from nothing (zero energy) and its existence to the present. Let's assume that it was born with the size of a proton and the mass energy of a proton. The energy of ΔE=(m_p)c^2 remains, and therefore, it has a very short Δt. Therefore, it is difficult to explain the birth of the universe from nothing (zero energy) and its existence to the present. In both cases, ΔE=(M_E)c^2 and ΔE=(m_p)c^2 remain, and it is difficult to explain the birth from nothing. However, let's assume the following situation calculated in this study. 1)If, Δt=t_p, ΔE=(5/6)(m_p)c^2, 2)If, Δt=(3/5)^(1/2)t_P, ΔE=(5/12)^(1/2)(m_p)c^2, The total energy of the system is 0. In other words, a mechanism that generates enormous mass (or energy) while maintaining a Zero Energy State is possible. If ΔE_T --> 0, Δt --> ∞ Δt where quantum fluctuations exist can be very large. In other words, Δt can be larger than the current age of the universe, and these quantum fluctuations can exist longer than the age of the universe. In addition, by the 2nd mechanism, since the negative gravitational potential energy exceeds the positive mass energy, the corresponding energy distribution has the characteristics of negative mass, and through this, it can explain the accelerated expansion of the early universe(Inflation) and the accelerated expansion of the current universe(Dark energy).

What did you read in my writing that made you think I tried to write E=E_k + E_p?