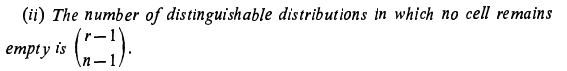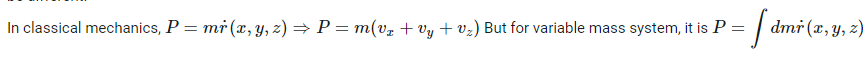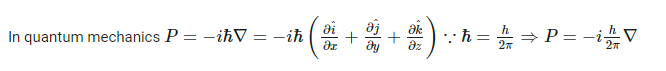Dhamnekar Win,odd

I did those computations for case(1) r=2, n=2 and case(2)r=2 and n=3. For case(1) The number of distinguishable distributions of 2 indistinguishable objects putting into 2 cells is 1 (equation or formula 1) and the numbers of distinguishable distributions of 2 distinguishable objects putting into 2 cells are 2(equation or formula 2) For case(2) The number of distinguishable distributions of 2 indistinguishable objects putting into 3 cells is -1 (equation or formula 1) and the number of distinguishable distributions of 2 distinguishable putting into 3 cells is 0(equation or formula 2) So, now how can we change the order of summation and use the binomial formula to express A(r, n+1) or in our case A(2,3) as the difference of two simple sums?

Assuming equation(2) to hold, how to express A(r-k, n) in equation (1) accordingly? How to change the order of summation and use the binomial formula to express A(r, n+1) as the difference of two simple sums as feller suggested? How to replace in the second sum v+1 by a new index of summation and use the following important property of binomial theorem [math]\binom{x}{r-1} + \binom{x}{r} = \binom{x+1}{r}[/math]?

The proof of the above formula was given in the book on probability by W.Feller

Did you go through the corrected equation (2) in my last post? v and k are the same variable i-e we are to select v or k cells from the n cells. That's it.

Please read my post under the heading "Elements of Combinatorial Analysis". Source " An Introduction to Probability Theory and Its Applications" by W.Feller, Chapter 2 and 4.

If I am not wrong, both formulas are meant for the computation of number of distinguishable distributions of indistinguishable r objects putting into n cells so that none of the n cells remains empty.

Corrected equation (1) [math] A(r, n+1)= \displaystyle\sum_{k=1}^{r} \binom{r}{k} A(r-k, n)[/math] Corrected equation (2) [math] A(r, n) = \displaystyle\sum_{v=0}^{n} (-1)^v\binom{n}{v}(n-v)^r[/math] Then the author W. Feller says to replace in the second sum v + 1 by a new index of summation and use important property of binomial theorem which I wrote in my original question

Some more information : This problem refers to the classical occupancy problem (Boltzmann-Maxwell statistics): that is, r balls are distributed among n cells and each of the [math] n^{r} [/math] possible distributions has probability [math]n^{-r}[/math]

How to use the given math hint to answer this question?

I have made mistakes in the computations of answers to question (a) and (b). Corrected answer:(a) [math]\binom{n + r -1}{r}= \binom{12}{9}= 220 [/math] where n=9 and r = 4 Corrected answer:(b) [math]220 + \binom{15}{13} + \binom{14}{12} + 2 \times \binom{13}{11} =220 +105 +91 + 156 =572[/math] Hence, author's answers are correct.

How to answer all these following questions? I am working on all these questions. Any chemistry help, or even correct answers to all these questions will be accepted.

In the above second question, [math] \nabla r , \hbar [/math] means gradient r (position vector) and reduced Plank's constant respectively.

Momentum is used to sense the amount of force applied to a moving object. With the help of Momentum, you can know the nature of the applied force on an object. Momentum is usually represented by the product of the mass and velocity of a moving object. But in this case of quantum mechanics, the equation of momentum will be different. How is this computed? How is this momentum computed in Quantum mechanics?

There is typographical error in the above question. Please read ' Is [math]Ca^{19+}[/math] one electron atom? '

Was the above question correctly stated and correctly answered? In [math]Ca^{19+}[/math], how many electron shells are there? answer is n=1,2,3,4 Then in ground state how can we found its valence electron in 6th shell or n=6? Is [math]Ca^{19+}[/math] one lectron atom?

Answers: REMOVED BY MODERATOR

An x-ray photoelectron spectroscopy experiment with an unidentified element, X, displays an emission spectrum with four distinct kinetic energies: [math] 5.9 \times 10^{-17} J, 2.53 \times 10^{-18} J,[/math] [math]2.59 \times 10^{-20} J, 2.67 \times 10^{-20} J [/math] (Assume the incident light has sufficient energy to eject any electron in the atom.) (a)Name all of the possible ground state atoms that could yield this spectrum. (b)Calculate the binding energy of an electron in the 2p orbital of element X if the x-rays used for the spectroscopy experiment had an energy of [math] 2.68 \times 10^{-16} J[/math] (c)Consider both the filled and unfilled orbitals of element X. Determine the number of: (1) total nodes in a 4d orbital (2)angular nodes in the [math]2p_y[/math] orbital (3)degenerate 5p orbitals How to answer all these questions?

How to prove (7.1)? How can we use the following two expansion formulas of CDF of normal distribution to prove (7.1) lemma?

Can I ask here statistics question? If yes, under which forum?

For additional information, refer to the following table:

Answer to d) 1)∆H = 17.4 kJ/mol 2)∆H = 8.7 kJ/mol 3)∆H= 4.35 kJ/mol Answer to e) Mechanism for this reaction is [math]1)N_2 + 2 O_2 \rightarrow 2 NO_2 \Delta H^\circ_f = 66.4 kJ/mol [/math] [math]2) N_2O_4 \rightarrow N_2 + 2 O_2 \Delta H^\circ_f = -9.16 kJ/mol [/math]