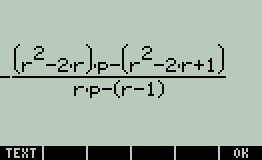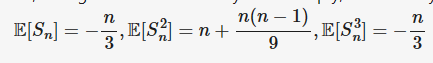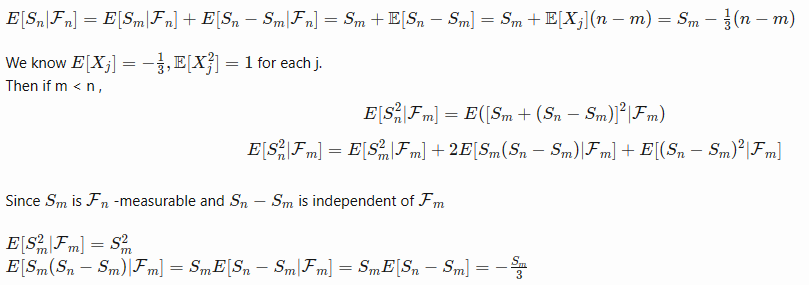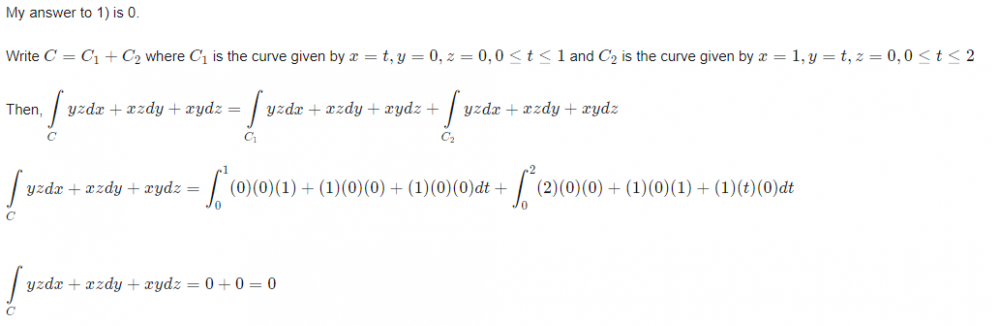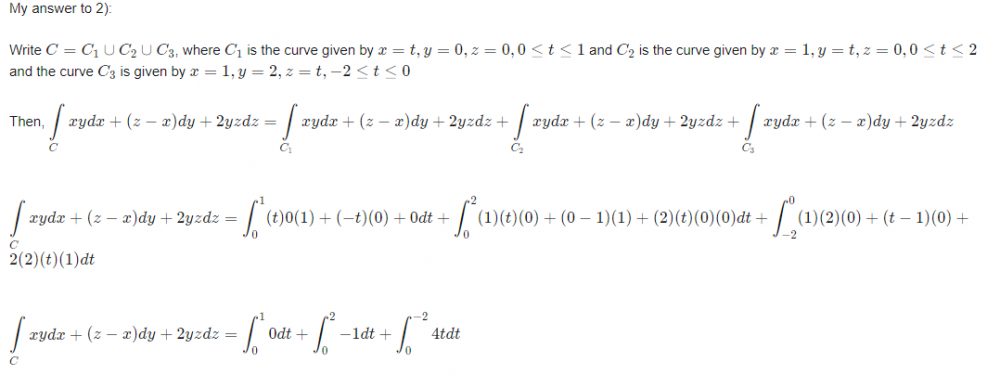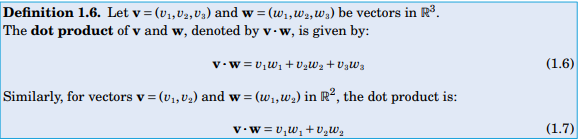Dhamnekar Win,odd

Author's answer to first case is \(\displaystyle\frac{\pi}{4}\) Do you disagree with that? Author assumed R be the radius of big circle, \(r_n\) be the radius in the outer layer of the big circle and \(\hat{r}_n\) be the radius of next inner layer circle of the big circle and \(R_n\) be the radius of the concentric circles inside the big circle. Following are the concentric circles. Do you agree with this author's assumption? Author computed the first case answer considering all these assumption. I think the following question with answer will be considered for more reference. Win_odd Dhamnekar (https://math.stackexchange.com/users/153118/win-odd-dhamnekar), Inscribed circles inside an equilateral triangle, URL (version: 2023-07-14): https://math.stackexchange.com/q/4735973

Do you agree with my derivation for the expression of \(P_n = \displaystyle\frac{n \cdot r_n}{2\cdot R -r_n}, R_2= R-r_n\). If not, I shall show you my working over these derivation.

If [math]\lim_{n \to \infty} n\cdot r_n \to 2 \cdot \pi \cdot R_2[/math] We got \(R-r_n = R_2 \Rightarrow R= R_2 + R_2= 2R_2\) Putting these values in our final expression for \(P_n\) we get \(\displaystyle\frac{2 \cdot \pi \cdot R_2}{4 \cdot R_2- R_2}=\frac23 \cdot \pi = P_n=2.0944 \) approx. But author's answer is \(P_n=0.9069\) approx. How is that?

In that case \(P_n\) would be $$\lim_{n \to \infty, r_n \to 0} P_n = \displaystyle\frac{n \cdot r_n}{2R- r_n}=0 $$ But author said \( \lim_{n \to \infty} P_n =\displaystyle\frac{\pi}{2\sqrt{3}}\)

But in this case [math]\lim_{n \to \infty} P_n = \infty [/math] Isn't it?

I am sorry. I wrongly computed \(P_n\) My new rectified \(P_n=\displaystyle\frac{n\cdot r_n}{2R-r_n}\)

@Genady, Would you explain your answer in details? There are two relations we know in the second case. \(1) (R -r_n) \cos{\displaystyle\frac{\pi}{n}} - \sqrt{(r_n +\hat{r}_n)^2 -\hat{r}_n^2} + \hat{r}_n = R_n, 2) \sin{\displaystyle\frac{\pi}{n}}=\displaystyle\frac{\hat{r}_n}{R_n - \hat{r}_n}\) The last relation said \(\hat{r}_n=\displaystyle\frac{R_n \cdot \sin{\displaystyle\frac{\pi}{n}}}{1 +\sin{\displaystyle\frac{\pi}{n}}}\). Replacing n in \(R_n \)by 2, and replacing \(\cos^2{\displaystyle\frac{\pi}{n}}\) by \(1- \sin^2{\displaystyle\frac{\pi}{n}}\) and squaring and expanding the brackets in the first relation we get \(R_2 = (R- r_n)\). Replacing the \(R_2\)'s value in the \(P_nR^2\pi = nr^2_n \pi + P_n\pi R^2_2\) we get \(P_n = \displaystyle\frac{\pi r_n}{2R-r_n} \) But author said \(P_n=\displaystyle\frac{\pi}{2\sqrt{3}}\) How is that?

For the two attached pictures below, let [math]{P_n}[/math] denote the proportion of the big circle covered by the small circles as function of the number of the small circle in the outer layer. Find the expression for [math]P_n[/math] and compute [math]\lim_{n\to \infty} P_n [/math]. Would you answer this question in details? **Author's answer to this question as follows:** Let R be the radius of the big circle, [math]r_n[/math] be the radius of the small circles in the outer layer, and \(R_n\) be the radius of the circle encompassing all small circles except those in the outer layer. Then in both cases \(P_n R^2\pi = n r^2_n \pi + P_n R^2_n \pi (\star)\) and \(\sin{\displaystyle\frac{\pi}{n} }= \displaystyle\frac{r_n}{R - r_n}\) In the first case, \(R_n= R- 2r_n\), giving $$ P_n = \displaystyle\frac{nr_n}{4(R-r_n)} = \displaystyle\frac{n \sin{\displaystyle\frac{\pi}{n}}}{4}, \lim_{n \to \infty} =\displaystyle\frac{\pi}{4}$$ In the second case we have \((R-r_n) \cos{\displaystyle\frac{r}{n}}- \sqrt{(r_n + \hat{r}_n )^2 - r^2_n} + \hat{r}_n = R_n \) where \(\hat{r}_n \) is the radius of the circle in the second outer layer \(\sin{\displaystyle\frac{\pi}{n}} = \displaystyle\frac{\hat{r}_n}{R_n -\hat{r}_n}\). The last two relations yield \(R_2\) to be substituted in \((\star)\) whence we get an expression for \(P_n\) and $$\lim_{n \to \infty} P_n = \displaystyle\frac{\pi}{2\sqrt{3}}$$ Now I agreed with author's answer in the first case. But in the second case, I got [math] \lim_{n\to\infty} P_n = \displaystyle\frac{\pi\cdot r_n}{2R- r_n}[/math]. How is [math]P_n = \displaystyle\frac{\pi}{2\sqrt{3}}[/math] ?

Let [math]X_i, i \geq 1[/math] be independent with [math] P( X _i = 1) =p, P(X_i =-1) =q = 1-p[/math] with [math]S_n= \displaystyle\sum_{i=1}^n X_i[/math] Show that [math](\frac{q}{p})^{S_n}, n \geq 1[/math] is a martingale with mean 1. Solution: Let's prove this step-by-step: 1) The [math]X_i[/math] are independent random variables with: [math]P(X_i = 1) = p[/math] [math]P(X_i = -1) = q = 1 - p[/math] 2) Let [math]S_n = \displaystyle\sum_{i=1}^n X_i[/math] be the partial sums. 3) Consider the stochastic process [math]Y_n = (\frac{q}{p})^{S_n}[/math]. 4) To show this is a martingale, we need to prove: [math]E[Y_{n+1} | Y_1, ..., Y_n] = Y_n[/math] 5) We have: [math]E[Y_{n+1} | Y_1, ..., Y_n] = E[(\frac{q}{p})^{S_{n+1}} | S_1, ..., S_n][/math] [math]= (\frac{q}{p})^{S_n} E[(\frac{q}{p})^{X_{n+1}}][/math] [math]= (\frac{q}{p})^{S_n} (q + p) = Y_n[/math] Where we have used the independence of the [math]X_i[/math] and the definition of conditional expectation. 6) Clearly [math]E[Y_n] = E[(\frac{q}{p})^{S_n}] = 1[/math] since [math]S_n[/math] has a symmetric distribution about 0. Therefore, [math](Y_n)_{n≥1} = ((\frac{q}{p})^{S_n})_{n≥1}[/math] is a martingale with mean 1. In my opinion, this solution is correct. Do you have any doubts?

Let E be a finite nonempty set and let [math]\Omega := E^{\mathbb{N}}[/math] be the set of all E-valued sequences [math] \omega = (\omega_n)_{n\in \mathbb{N}}[/math]. For any [math] \omega_1, \dots,\omega_n \in E[/math] Let [math][\omega_1, \dots,\omega_n]= \{\omega^, \in \Omega : \omega^,_i = \omega_i \forall i =1,\dots,n \}[/math] be the set of all sequences whose first n values are [math]\omega_1,\dots, \omega_n[/math]. Let [math]\mathcal{A}_0 =\{\emptyset\}[/math] for [math]n\in \mathbb{N}[/math] define [math]\mathcal{A}_n :=\{[\omega_1,\dots,\omega_n] : \omega_1,\dots, \omega_n \in E\}[/math]. Hence show that [math]\mathcal{A}= \bigcup_{n=0}^\infty \mathcal{A}_n[/math] is a semiring but is not a ring if (#E >1). My answer: Let's consider an example where [math]E = \{0,1\}[/math] and [math]\Omega = E^{\mathbb{N}}[/math] is the set of all E-valued sequences. For any [math]\omega_1,\dots,\omega_n \in E[/math], we have [math][\omega_1,\dots,\omega_n] = \{\omega \in \Omega : \omega_i = \omega_i \forall i = 1,\dots,n\}[/math] which is the set of all sequences whose first [math]n[/math] values are [math]\omega_1,\dots,\omega_n[/math]. Let [math]\mathcal{A}_0 = \{\emptyset\}[/math] and for [math]n \in \mathbb{N}[/math] define [math]\mathcal{A}_n := \{[\omega_1,\dots,\omega_n] : \omega_1,\dots,\omega_n \in E\}.[/math] Hence [math]\mathcal{A} = \bigcup_{n=0}^\infty \mathcal{A}_n[/math] is a semiring but not a ring if # E > 1. To see why [math]\mathcal{A}[/math] is a semiring, let's verify that it satisfies the three conditions for a semiring. First, it contains the empty set because [math]\mathcal{A}_0 = \{\emptyset\}[/math] and [math]\mathcal{A} = \bigcup_{n=0}^\infty \mathcal{A}_n[/math]. Second, for any two sets [math]A,B \in \mathcal{A}[/math], their difference [math]B \setminus A[/math] is a finite union of mutually disjoint sets in [math]\mathcal{A}[/math]. For example, let [math]A = [0][/math] and [math]B = [1][/math], then [math]B \setminus A = [1][/math], which is in [math]\mathcal{A}[/math]. Third, [math]\mathcal{A}[/math] is closed under intersection. For example, let [math]A = [0][/math] and [math]B = [1][/math], then [math]A \cap B = \emptyset[/math], which is in [math]\mathcal{A}[/math]. However, [math]\mathcal{A}[/math] is not a ring because it does not satisfy all three conditions for a ring. Specifically, it does not satisfy condition (ii) for a ring, which requires that [math]\mathcal{A}[/math] be closed under set difference. For example, let [math]A = [0,0]][/math] and [math]B = [0,1][/math], then [math]B \setminus A = [0,1] \setminus [0,0] = [0,1][/math], which is not in [math]\mathcal{A}[/math]. I hope this example helps to illustrate why [math]\mathcal{A}[/math] is a semiring but not a ring if the cardinality of [math]E[/math] is greater than 1. Is this answer correct?

Read here the whole computation: [math]\displaystyle\frac{p}{p+(1-r)(1-p)} \cdot 1 + \left[1-\displaystyle\frac{p}{p+(1-r)(1-p)}\right]\cdot (1-r)= -\displaystyle\frac{p\cdot(r^2-2\cdot r)-(r^2-2r +1)}{r \cdot p -(r-1)}= 1-\displaystyle\frac{r\cdot (1-r) \cdot (1-p)}{p + (1-r)\cdot (1-p)}[/math]

If we solve, P(vote in same way next time | V) = [p / [p + (1-r)*(1-p)]] * 1 + [1 - p / [p + (1-r)*(1-p)]] * (1-r) This simplifies to: So,final answer ishttps://www.scienceforums.net/topic/131457-computing-the-probability-of-voting-of-the-member-of-parliament/?do=findComment&comment=1238311

It is given in the question ab initio. It is the division in the second term, not multiplication.

Yes. You are correct. The final answer is [math] 1-\displaystyle\frac{r(1-p)(1-r)}{(p + (1-r)(1-p))}[/math]

[math]\frac45[/math] is a small whole number ratio that supports the law of multiple proportions. In the compound X, 0.8 atoms of carbon required compared to the carbon atoms required in the compound Y, for each atom of Hydrogen.

1) The data provided in the question indicates that compound X and Y are two different compounds formed by the combination of carbon and Hydrogen in indefinite proportions. In this case, the ratio of hydrogen to carbon in compound X is 2.96 g / 14.13 g = 0.21 and the ratio of hydrogen to carbon in compound Y is 3.34 g / 19.91 g = 0.17. These ratios are not equal, so the data does not support the law of definite proportions. Additionally, the ratio of these two ratios is 0.17 / 0.21 = 0.81, which is a small whole number, so the data supports the law of multiple proportions. 2) The data provided in the question indicates that compounds A and B are two different compounds formed by the combination of carbon and oxygen in different proportions. Compound A has one-half as much oxygen per amount of carbon (or twice as much carbon per amount of oxygen) as compound B. This means that for a fixed amount of carbon, compound A has half the amount of oxygen compared to compound B. Similarly, for a fixed amount of oxygen, compound A has twice the amount of carbon compared to compound B. This is an example of the law of multiple proportions. One possible pair of compounds that would fit the relationship described in the question are carbon monoxide (CO) and carbon dioxide (CO2). Both of these compounds are formed by the combination of carbon and oxygen. In carbon monoxide, there is one oxygen atom for every carbon atom, while in carbon dioxide, there are two oxygen atoms for every carbon atom. This means that for a fixed amount of carbon, carbon monoxide has half the amount of oxygen compared to carbon dioxide. Similarly, for a fixed amount of oxygen, carbon monoxide has twice the amount of carbon compared to carbon dioxide. This is an example of the law of multiple proportions.

1) A sample of compound X (a clear, colorless, combustible liquid with a noticeable odor) is analyzed and found to contain 14.13 g carbon and 2.96 g hydrogen. A sample of compound Y (a clear, colorless, combustible liquid with a noticeable odor that is slightly different from X’s odor) is analyzed and found to contain 19.91 g carbon and 3.34 g hydrogen. Are these data an example of the law of definite proportions, the law of multiple proportions, or neither? What do these data tell you about substances X and Y? 2)A sample of compound A (a clear, colorless gas) is analyzed and found to contain 4.27 g carbon and 5.69 g oxygen. A sample of compound B (also a clear, colorless gas) is analyzed and found to contain 5.19 g carbon and 13.84 g oxygen. Are these data an example of the law of definite proportions, the law of multiple proportions, or neither? What do these data tell you about substances A and B? My answers: 1) The data provided in the question is not an example of either the law of definite proportions or the law of multiple proportions. The law of definite proportions states that a chemical compound always contains exactly the same proportion of elements by mass. The law of multiple proportions states that when two elements combine to form more than one compound, the masses of one element that combine with a fixed mass of the other element are in a ratio of small whole numbers. In this case, the ratio of hydrogen to carbon in compound X is 2.96 g / 14.13 g = 0.21 and the ratio of hydrogen to carbon in compound Y is 3.34 g / 19.91 g = 0.17. These ratios are not equal, so the data does not support the law of definite proportions. Additionally, the ratio of these two ratios is 0.17 / 0.21 = 0.81, which is not a small whole number, so the data does not support the law of multiple proportions either. Based on this data alone, it is not possible to determine any additional information about substances X and Y. 2) The data provided in the question is an example of the law of multiple proportions. This law states that when two elements combine to form more than one compound, the masses of one element that combine with a fixed mass of the other element are in a ratio of small whole numbers. In this case, the ratio of oxygen to carbon in compound A is 5.69 g / 4.27 g = 1.33 and the ratio of oxygen to carbon in compound B is 13.84 g / 5.19 g = 2.67. The ratio of these two ratios is 2.67 / 1.33 = 2, which is a small whole number. This tells us that substances A and B are two different compounds formed by the combination of carbon and oxygen in different proportions.

Parliament contains a proportion p of Labour members, who are incapable of changing their minds about anything, and a proportion 1 − p of Conservative members who change their minds completely at random (with probability r) between successive votes on the same issue. A randomly chosen member is noticed to have voted twice in succession in the same way. What is the probability that this member will vote in the same way next time? My answer: Let's solve this problem step by step. First, let's find the probability that the member is a Labour member given that they have voted twice in succession in the same way. We can use Bayes' theorem for this. Let L be the event that the member is a Labour member and V be the event that the member has voted twice in succession in the same way. Then, we have: P(L|V) = P(V|L) * P(L) / P(V) Since a Labour member is incapable of changing their mind, P(V|L) = 1. The prior probability of a member being a Labour member is given as p, so P(L) = p. To find P(V), we can use the law of total probability: P(V) = P(V|L) * P(L) + P(V|Lc) * P(Lc) where Lc is the event that the member is not a Labour member (i.e., they are a Conservative member). As mentioned earlier, P(V|L) = 1 and P(L) = p. Since a Conservative member changes their mind completely at random with probability r between successive votes on the same issue, the probability that they vote in the same way twice in succession is (1-r), so P(V|Lc) = (1-r). The prior probability of a member being a Conservative member is given as (1-p), so P(Lc) = (1-p). Plugging these values into the equation above, we get: P(V) = 1 * p + (1-r) * (1-p) Now we can plug this value into our equation for P(L|V): P(L|V) = 1 * p / [p + (1-r)*(1-p)] Now that we have found the probability that the member is a Labour member given that they have voted twice in succession in the same way, we can find the probability that they will vote in the same way next time. Since a Labour member is incapable of changing their mind and a Conservative member changes their mind completely at random with probability r between successive votes on the same issue, this probability is: P(vote in same way next time | V) = P(L|V) * 1 + [1 - P(L|V)] * (1-r) Plugging in our value for P(L|V), we get: P(vote in same way next time | V) = [p / [p + (1-r)*(1-p)]] * 1 + [1 - p / [p + (1-r)*(1-p)]] * (1-r) This simplifies to: P(vote in same way next time | V) = 1 - r(1-p)/(p + (1-r)(1-p)) This is our final answer. Is this answer correct? Note: credit for this answer goes to Microsoft Artificial Intelligence powered chat.

My answers: 1. - n (n-1) [imath] -\displaystye\frac{n(n-1)(n-2)}{27}[/imath] 2.

My answer: As each one of the 30 squares represents one state of the 30-stateMarkov chain, I prepared the transition matrix 'x' in octave. Here is matrix 'x'.. >> x x = Columns 1 through 14: 1.0000 0 0 0 0 0 0 0 0 0 0 0 0 0 0.3333 0.1667 0.5000 0 0 0 0 0 0 0 0 0 0 0 0 0.3333 0.1667 0.5000 0 0 0 0 0 0 0 0 0 0 0 0.3333 0 0.1667 0 0.5000 0 0 0 0 0 0 0 0 0 0 0.3333 0 0.1667 0 0.5000 0 0 0 0 0 0 0 0 0 0.3333 0 0 0.1667 0 0 0.5000 0 0 0 0 0 0 0 0 0.3333 0 0 0.1667 0 0 0.5000 0 0 0 0 0 0 0 0.3333 0 0 0 0.1667 0 0 0 0.5000 0 0 0 0 0 0 0.3333 0 0 0 0.1667 0 0 0 0.5000 0 0 0 0 0 0.3333 0 0 0 0 0.1667 0 0 0 0 0 0 0 0 0 0.3333 0 0 0 0 0.1667 0 0 0 0 0 0 0 0 0.3333 0 0 0 0 0 0.1667 0 0 0 0 0 0 0 0 0.3333 0 0 0 0 0 0.1667 0 0 0 0 0 0 0 0.3333 0 0 0 0 0 0 0.1667 0 0 0 0 0 0 0 0.3333 0 0 0 0 0 0 0 0 0 0 0 0 0 0.3333 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.3333 0 0 0 0 0 0 0 0 0 0 0 0 0 0.3333 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.3333 0 0 0 0 0 0 0 0 0 0 0 0 0 0.3333 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.3333 0 0 0 0 0 0 0 0 0 0 0 0 0 0.3333 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.3333 0 0 0 0 0 0 0 0 0 0 0 0 0 0.3333 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.3333 0 0 0 0 0 0 0 0 0 0 0 0 0 0.3333 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.3333 0 0 0 0 0 0 0 0 0 0 0 0 0 0.3333 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Columns 15 through 28: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.5000 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.5000 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.5000 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.5000 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.5000 0 0 0 0 0 0 0 0.1667 0 0 0 0 0 0 0.5000 0 0 0 0 0 0 0 0.1667 0 0 0 0 0 0 0 0.5000 0 0 0 0 0 0 0.1667 0 0 0 0 0 0 0 0.5000 0 0 0 0 0 0 0.1667 0 0 0 0 0 0 0 0 0.5000 0 0 0 0 0 0.1667 0 0 0 0 0 0 0 0 0.5000 0 0 0 0 0 0.1667 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.1667 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.1667 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.1667 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.1667 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.1667 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.1667 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.1667 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.1667 0.3333 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Columns 29 and 30: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.5000 0 0.5000 0 0.5000 0 0.5000 0 0.5000 0 0.5000 0 0.5000 0 0.5000 0 0.5000 0.1667 0.5000 0 1.0000 >> x^1000 ans = Columns 1 through 14: 1.0000 0 0 0 0 0 0 0 0 0 0 0 0 0 0.8536 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.7561 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.6910 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.6235 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.5826 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.5351 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.5105 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.4670 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.4312 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.4117 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.3902 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.3626 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.3129 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.3030 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.2978 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.2738 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.2619 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.2476 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.1725 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.1647 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.1647 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.1561 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.1561 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.1450 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.1450 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.1252 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.1252 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.1212 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Columns 15 through 28: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0.0000 0 0.0000 0 0 0.0000 0.0000 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Columns 29 and 30: 0 0 0 0.1464 0 0.2439 0 0.3090 0 0.3765 0 0.4174 0 0.4649 0 0.4895 0 0.5330 0 0.5688 0 0.5883 0 0.6098 0 0.6374 0 0.6871 0 0.6970 0 0.7022 0 0.7262 0 0.7381 0 0.7524 0 0.8275 0 0.8353 0 0.8353 0 0.8439 0 0.8439 0 0.8550 0 0.8550 0 0.8748 0 0.8748 0 0.8788 0 1.0000 x(5,30)=0.3765 imply that if any player starts from the x(5,5)=$200000 state, he/she has only 37.65% chance to get millionairedom status. I think my answer is correct. Isn't it?

This is the exercise 1.1 on page 33, of the book titled " Elementary Calculus of Financial Mathematics" written by Professor A. G. Roberts. Visit https://tuck.adelaide.edu.au/ecfm.php

I think stochastic mathematics question can be posted under this forum.

Get your friends and family to play this simple little game that illustrates a key aspect of stochastic mathematics in application to finance. 1. Draw on a big sheet of paper a sequence of 30 squares and label them consecutively 0 (bankrupt), 1, 1, 2, 2, 3, 3, 4, . . . , 14, 14, 15 (millionairedom). Each of these squares represents one state in a 30-state Markov chain. Imagine each state represents the value of some asset such as the value of a small business that each player is managing. 2. Give each player a token and a six-sided die. 3. At the start place each token on the second “2”, the fifth state. Imagine this corresponds to the small business having an initial value of $200,000. 4. Each turn in the game corresponds to, say, one year in time. In each year the business may be poor or may grow. Thus in each turn each player rolls his/her die and moves according to the following rules: • If a player rolls a 1 or 2, then he/she moves down some states; • if a player rolls a 3, he/she stays in the same state; • if a player rolls a 4, 5, or 6, he/she moves up some states. But the number of states (squares) a player moves is given by the number written in each square. Thus in the first move, because the fifth square/state is a “2,” a player moving up moves from the fifth square to the seventh square, and a player moving down moves to the third square. That the number written in each square is (roughly) proportional to the position of the square in the sequence corresponds to the financial reality that small businesses usually grow/shrink by small amounts, whereas large companies grow/shrink by large amounts. Investors expect returns in proportion to their investments. 5. Each player continues to role his/her die and move until reaching 0 or 15. That is, players continue to operate their businesses until they either go bankrupt or reach millionairedom. Questions: 1. Why do you expect each business to grow? That is, why do you expect each player to reach the “millionairedom” state? 2. When you play the game, roughly what proportion of players reach millionairedom? What proportion go bankrupt? 3. How do you explain the actual results? How would you answer all the above three questions? What are your answers to all of these above three questions? How can I write a program in R or in Octave to simulate this game?

In a chess tournament, each participant plays with every other participant exactly once. Each participant gets 1 point for a winning a game, 0.5 points for a draw and no point for a loosing a game. At most, how many of the 40 participants can score 24 points or more? My attempt to answer this question: There will be [math]\binom{40}{2}=780[/math] games in this chess tournament. Now each player will play 39 game. The probability of winning a game is [math]\frac13[/math]. Probability of loosing a game is [math]\frac13[/math] and the probability of making a game draw is [math]\frac13[/math]. So, out of 780 games, 260 games will be won by some players, 260 games will be lost and 260 games will be drawn. How can we proceed from here to answer this question?