Dhamnekar Win,odd

I want to ask the following types of OPERATIONS RESEARCH questions. Where can I ask them? 1) Linear Programming( formulation of graphic method) 2)Linear programming (Simplex method) 3)Linear Programming( the dual Problem and post-optimality analysis) 4) Transportation problems 5) Assignment problems 6)The sequencing problems 7) Replacement decisions 8)Queuing theory 9) Decision theory and decision analysis 10)Theory of games 11) Statistical quality control 12)Inventory management 13)Investment analysis 14)Simulation 15)Work study and value analysis 16)Goal, Integer and Dynamic programming 17)Project management PERT and CPM 18)Markov analysis

Success rate is 75% because 12P((B−A)>0|A>0)+12P((B−A)≤0|A<0)=0.75 in the long term. If A is +ve, I shall tell B is lower than A and if A is -ve, I shall tell B is larger than A.🤔🤔🤔🤔 ☺️☺️☺️☺️☺️☺️☺️

I followed this author's equation using mathematical reasoning and logical sense.☺️ But I don't know to derive its proof.🤔. By the way, another author, using properties of uniform distribution and geometry of the circle answered this question as below: Uniformly independently distribute \(n+2\) points on a circle of circumference \(1\). Uniformly randomly pick one of the points as point \(0\). By symmetry, the expected length of the interval between its neighbours is \(\frac2{n+2}\). The distance to its nearest neighbour is uniformly distributed between \(0\) and half of that, so the expected distance to the nearest neighbour is \(\frac1{2(n+2)}\), and accordingly the expected distance to the other neighbour is \(\frac3{2(n+2)}\). Now uniformly randomly pick another one of the \(n+2\)points at which to cut the circle into an interval (leaving n other points). With probability \(\frac1{n+1}\), the nearest neighbour of point \(0\) is picked, and its other neighbour becomes its nearest neighbour. Thus, the expected distance to the nearest neighbour on the interval is $$\frac1{n+1}\cdot\frac3{2(n+2)}+\frac n{n+1}\cdot\frac1{2(n+2)}=\frac{n+3}{2(n+1)(n+2)}\;.$$ Now to answer your question: \(X_0\) is uniformly distributed on [0,1], so the expected value of the expression is the integral over that interval. (The \(\mathrm dx\) in that integral is misplaced.) The next equality uses [math]\mathsf E=\int_0^\infty\mathsf P(U\ge u)\mathrm du;,[/math] for the non-negative random variable [math]U=\min_{1\le i\le n}|x-X_i|\;,[/math] with [math]\mathsf P(U\ge u)=P(|X_0-x|\ge u)^n\;,[/math] since the minimum is \(\ge u\) exactly if all n distances are \(\ge u\), all with the same probability \(P(|X_0-x|\ge u)\). (The index \(0\) here is slightly confusing, since x is the dummy variable for \(X_0\); I would have written \(X_1\), but it doesn’t matter since the \(n+1\) variables are i.i.d.) The next equality adds up the lenghts of the two regions where the inequality is satisfied; the \(\max(\cdot,0)\) construction ensures that nothing is added if one of these regions doesn’t exist and the corresponding difference is negative. The next equality makes the three cases that can occur for \(x\in[0,\frac12]\) explicit, in which zero, one or two of the maximum functions vanish, respectively. The next equality splits the inner integral into the first two cases (as the integrand is zero in the third) and uses symmetry to replace the outer integral over ][0,1] by twice the integral over \([0,\frac12]\). The rest is just standard integration. I don't understand this answer. Would any member of this forum explain this answer?

I don't understand the author's solution given to the following question. Would any member of this forum take some efforts to explain this solution?

Author has given the success rate in his solution. Please read it.☺️

My answer is wrong. Author's solution is correct.☺️

Suppose we play the game where I draw a N(0, 1) random number A, show it to you, then draw another independent N(0, 1) one B, but before showing it to you ask you to guess whether B will be larger than A or not. If you are right, you win if you are wrong you lose. What is your strategy, and what will be your long term success rate if we keep playing? Author's Solution: Since the numbers are zero-mean, the strategy is to guess the sign of the difference B − A as positive if A < 0, and negative otherwise. The long-term success rate will be \(\frac12 P(B-A) > 0| A < 0) + \frac12 P(B-A) \leq 0 | A \geq 0)\) Due to the symmetry, and the fact that P(A=0)=0 , the above expression simplifies to P(B-A) > 0 |A < 0). Plotting on the (a, b) Cartesian plane the part of the region a < 0 where b − a > 0, we see that this is one and a half quadrants out of the two comprising the full a < 0 region. Therefore, due to the radial symmetry of the Gaussian two-dimensional distribution with zero correlation, we conclude that the success rate is \(\frac34\). My answer: The game you’re describing involves guessing whether a second independent draw from a standard normal distribution (N(0,1)) will be larger than the first. Given that both A and B are drawn from the same distribution, there is no information about B that can be inferred from A. Therefore, the best strategy is to always guess that B will be larger than A, or always guess that B will be smaller than A. Both strategies have the same success rate. The long-term success rate of this strategy is 50%. This is because, for two independent draws from the same distribution, the probability that the second draw is larger than the first is the same as the probability that the first draw is larger than the second. In mathematical terms, if A and B are independent and identically distributed (i.i.d.) random variables, then: P(B > A) = P(A < B) = 0.5 So, no matter how many times we play this game, your long-term success rate will converge to 50%. Whose answer is correct? If Author's solution is correct, would you show me graphically how can the part of the region a < 0 where b-a > 0 is one and half quadrants out of the two quadrants comprising the full a < 0 region?

KJW, I solved my query myself. ☺️

How did you get I got \( 1 +\alpha = \displaystyle\frac{3\cdot |{\phi}| +\phi^2 -4}{2\phi^2 -2}\) How is that? Where I am wrong?

@KJW, How did you arrive at this equation pointed out by arrow? Would you show me its computations? What is mathematical reasoning (mathematical logic ) behind this computations?

KJW, How did you derive the distance from the center of circle lying in the second outermost circle to the center of the larger circle is \(\alpha(R-r) ?\) Can you give me a real world example? Suppose R=10, r=2 and \(\alpha (R -r) = 1\) So, using simple mathematical reasoning, the distance from the center of the circle lying in the second outermost layer to the center of the larger circle is 4 + 1 = 5. But using your formula \(\alpha (R-r)= \displaystyle\frac12(10- 2)= 4\). How is that? Where I am wrong?

KJW, Would you show me this triangle graphically? 🤔☺️

Author's answer to first case is \(\displaystyle\frac{\pi}{4}\) Do you disagree with that? Author assumed R be the radius of big circle, \(r_n\) be the radius in the outer layer of the big circle and \(\hat{r}_n\) be the radius of next inner layer circle of the big circle and \(R_n\) be the radius of the concentric circles inside the big circle. Following are the concentric circles. Do you agree with this author's assumption? Author computed the first case answer considering all these assumption. I think the following question with answer will be considered for more reference. Win_odd Dhamnekar (https://math.stackexchange.com/users/153118/win-odd-dhamnekar), Inscribed circles inside an equilateral triangle, URL (version: 2023-07-14): https://math.stackexchange.com/q/4735973

Do you agree with my derivation for the expression of \(P_n = \displaystyle\frac{n \cdot r_n}{2\cdot R -r_n}, R_2= R-r_n\). If not, I shall show you my working over these derivation.

If [math]\lim_{n \to \infty} n\cdot r_n \to 2 \cdot \pi \cdot R_2[/math] We got \(R-r_n = R_2 \Rightarrow R= R_2 + R_2= 2R_2\) Putting these values in our final expression for \(P_n\) we get \(\displaystyle\frac{2 \cdot \pi \cdot R_2}{4 \cdot R_2- R_2}=\frac23 \cdot \pi = P_n=2.0944 \) approx. But author's answer is \(P_n=0.9069\) approx. How is that?

In that case \(P_n\) would be $$\lim_{n \to \infty, r_n \to 0} P_n = \displaystyle\frac{n \cdot r_n}{2R- r_n}=0 $$ But author said \( \lim_{n \to \infty} P_n =\displaystyle\frac{\pi}{2\sqrt{3}}\)

But in this case [math]\lim_{n \to \infty} P_n = \infty [/math] Isn't it?

I am sorry. I wrongly computed \(P_n\) My new rectified \(P_n=\displaystyle\frac{n\cdot r_n}{2R-r_n}\)

@Genady, Would you explain your answer in details? There are two relations we know in the second case. \(1) (R -r_n) \cos{\displaystyle\frac{\pi}{n}} - \sqrt{(r_n +\hat{r}_n)^2 -\hat{r}_n^2} + \hat{r}_n = R_n, 2) \sin{\displaystyle\frac{\pi}{n}}=\displaystyle\frac{\hat{r}_n}{R_n - \hat{r}_n}\) The last relation said \(\hat{r}_n=\displaystyle\frac{R_n \cdot \sin{\displaystyle\frac{\pi}{n}}}{1 +\sin{\displaystyle\frac{\pi}{n}}}\). Replacing n in \(R_n \)by 2, and replacing \(\cos^2{\displaystyle\frac{\pi}{n}}\) by \(1- \sin^2{\displaystyle\frac{\pi}{n}}\) and squaring and expanding the brackets in the first relation we get \(R_2 = (R- r_n)\). Replacing the \(R_2\)'s value in the \(P_nR^2\pi = nr^2_n \pi + P_n\pi R^2_2\) we get \(P_n = \displaystyle\frac{\pi r_n}{2R-r_n} \) But author said \(P_n=\displaystyle\frac{\pi}{2\sqrt{3}}\) How is that?

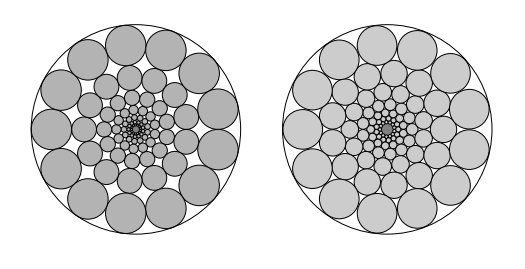
For the two attached pictures below, let [math]{P_n}[/math] denote the proportion of the big circle covered by the small circles as function of the number of the small circle in the outer layer. Find the expression for [math]P_n[/math] and compute [math]\lim_{n\to \infty} P_n [/math]. Would you answer this question in details? **Author's answer to this question as follows:** Let R be the radius of the big circle, [math]r_n[/math] be the radius of the small circles in the outer layer, and \(R_n\) be the radius of the circle encompassing all small circles except those in the outer layer. Then in both cases \(P_n R^2\pi = n r^2_n \pi + P_n R^2_n \pi (\star)\) and \(\sin{\displaystyle\frac{\pi}{n} }= \displaystyle\frac{r_n}{R - r_n}\) In the first case, \(R_n= R- 2r_n\), giving $$ P_n = \displaystyle\frac{nr_n}{4(R-r_n)} = \displaystyle\frac{n \sin{\displaystyle\frac{\pi}{n}}}{4}, \lim_{n \to \infty} =\displaystyle\frac{\pi}{4}$$ In the second case we have \((R-r_n) \cos{\displaystyle\frac{r}{n}}- \sqrt{(r_n + \hat{r}_n )^2 - r^2_n} + \hat{r}_n = R_n \) where \(\hat{r}_n \) is the radius of the circle in the second outer layer \(\sin{\displaystyle\frac{\pi}{n}} = \displaystyle\frac{\hat{r}_n}{R_n -\hat{r}_n}\). The last two relations yield \(R_2\) to be substituted in \((\star)\) whence we get an expression for \(P_n\) and $$\lim_{n \to \infty} P_n = \displaystyle\frac{\pi}{2\sqrt{3}}$$ Now I agreed with author's answer in the first case. But in the second case, I got [math] \lim_{n\to\infty} P_n = \displaystyle\frac{\pi\cdot r_n}{2R- r_n}[/math]. How is [math]P_n = \displaystyle\frac{\pi}{2\sqrt{3}}[/math] ?

Let [math]X_i, i \geq 1[/math] be independent with [math] P( X _i = 1) =p, P(X_i =-1) =q = 1-p[/math] with [math]S_n= \displaystyle\sum_{i=1}^n X_i[/math] Show that [math](\frac{q}{p})^{S_n}, n \geq 1[/math] is a martingale with mean 1. Solution: Let's prove this step-by-step: 1) The [math]X_i[/math] are independent random variables with: [math]P(X_i = 1) = p[/math] [math]P(X_i = -1) = q = 1 - p[/math] 2) Let [math]S_n = \displaystyle\sum_{i=1}^n X_i[/math] be the partial sums. 3) Consider the stochastic process [math]Y_n = (\frac{q}{p})^{S_n}[/math]. 4) To show this is a martingale, we need to prove: [math]E[Y_{n+1} | Y_1, ..., Y_n] = Y_n[/math] 5) We have: [math]E[Y_{n+1} | Y_1, ..., Y_n] = E[(\frac{q}{p})^{S_{n+1}} | S_1, ..., S_n][/math] [math]= (\frac{q}{p})^{S_n} E[(\frac{q}{p})^{X_{n+1}}][/math] [math]= (\frac{q}{p})^{S_n} (q + p) = Y_n[/math] Where we have used the independence of the [math]X_i[/math] and the definition of conditional expectation. 6) Clearly [math]E[Y_n] = E[(\frac{q}{p})^{S_n}] = 1[/math] since [math]S_n[/math] has a symmetric distribution about 0. Therefore, [math](Y_n)_{n≥1} = ((\frac{q}{p})^{S_n})_{n≥1}[/math] is a martingale with mean 1. In my opinion, this solution is correct. Do you have any doubts?

Let E be a finite nonempty set and let [math]\Omega := E^{\mathbb{N}}[/math] be the set of all E-valued sequences [math] \omega = (\omega_n)_{n\in \mathbb{N}}[/math]. For any [math] \omega_1, \dots,\omega_n \in E[/math] Let [math][\omega_1, \dots,\omega_n]= \{\omega^, \in \Omega : \omega^,_i = \omega_i \forall i =1,\dots,n \}[/math] be the set of all sequences whose first n values are [math]\omega_1,\dots, \omega_n[/math]. Let [math]\mathcal{A}_0 =\{\emptyset\}[/math] for [math]n\in \mathbb{N}[/math] define [math]\mathcal{A}_n :=\{[\omega_1,\dots,\omega_n] : \omega_1,\dots, \omega_n \in E\}[/math]. Hence show that [math]\mathcal{A}= \bigcup_{n=0}^\infty \mathcal{A}_n[/math] is a semiring but is not a ring if (#E >1). My answer: Let's consider an example where [math]E = \{0,1\}[/math] and [math]\Omega = E^{\mathbb{N}}[/math] is the set of all E-valued sequences. For any [math]\omega_1,\dots,\omega_n \in E[/math], we have [math][\omega_1,\dots,\omega_n] = \{\omega \in \Omega : \omega_i = \omega_i \forall i = 1,\dots,n\}[/math] which is the set of all sequences whose first [math]n[/math] values are [math]\omega_1,\dots,\omega_n[/math]. Let [math]\mathcal{A}_0 = \{\emptyset\}[/math] and for [math]n \in \mathbb{N}[/math] define [math]\mathcal{A}_n := \{[\omega_1,\dots,\omega_n] : \omega_1,\dots,\omega_n \in E\}.[/math] Hence [math]\mathcal{A} = \bigcup_{n=0}^\infty \mathcal{A}_n[/math] is a semiring but not a ring if # E > 1. To see why [math]\mathcal{A}[/math] is a semiring, let's verify that it satisfies the three conditions for a semiring. First, it contains the empty set because [math]\mathcal{A}_0 = \{\emptyset\}[/math] and [math]\mathcal{A} = \bigcup_{n=0}^\infty \mathcal{A}_n[/math]. Second, for any two sets [math]A,B \in \mathcal{A}[/math], their difference [math]B \setminus A[/math] is a finite union of mutually disjoint sets in [math]\mathcal{A}[/math]. For example, let [math]A = [0][/math] and [math]B = [1][/math], then [math]B \setminus A = [1][/math], which is in [math]\mathcal{A}[/math]. Third, [math]\mathcal{A}[/math] is closed under intersection. For example, let [math]A = [0][/math] and [math]B = [1][/math], then [math]A \cap B = \emptyset[/math], which is in [math]\mathcal{A}[/math]. However, [math]\mathcal{A}[/math] is not a ring because it does not satisfy all three conditions for a ring. Specifically, it does not satisfy condition (ii) for a ring, which requires that [math]\mathcal{A}[/math] be closed under set difference. For example, let [math]A = [0,0]][/math] and [math]B = [0,1][/math], then [math]B \setminus A = [0,1] \setminus [0,0] = [0,1][/math], which is not in [math]\mathcal{A}[/math]. I hope this example helps to illustrate why [math]\mathcal{A}[/math] is a semiring but not a ring if the cardinality of [math]E[/math] is greater than 1. Is this answer correct?

Read here the whole computation: [math]\displaystyle\frac{p}{p+(1-r)(1-p)} \cdot 1 + \left[1-\displaystyle\frac{p}{p+(1-r)(1-p)}\right]\cdot (1-r)= -\displaystyle\frac{p\cdot(r^2-2\cdot r)-(r^2-2r +1)}{r \cdot p -(r-1)}= 1-\displaystyle\frac{r\cdot (1-r) \cdot (1-p)}{p + (1-r)\cdot (1-p)}[/math]

If we solve, P(vote in same way next time | V) = [p / [p + (1-r)*(1-p)]] * 1 + [1 - p / [p + (1-r)*(1-p)]] * (1-r) This simplifies to: So,final answer ishttps://www.scienceforums.net/topic/131457-computing-the-probability-of-voting-of-the-member-of-parliament/?do=findComment&comment=1238311