Kartazion

I am a beginner with Lagrangian field theory. The worst are the tensor fields and spinor fields. But the thing I say to myself is that a lot of these equations (in quantum chromodynamics) are simply an incomprehensible bypass of Pauli exclusion. Which is not a problem with the single particle principle. How does electromagnetism intervene with the strong interaction for quark operation? Or do you have a specific reference? Thank you in advance.

Hello Markus, The core makes photon? This is in the case of disintegration? Ok You're right, it's complicated.

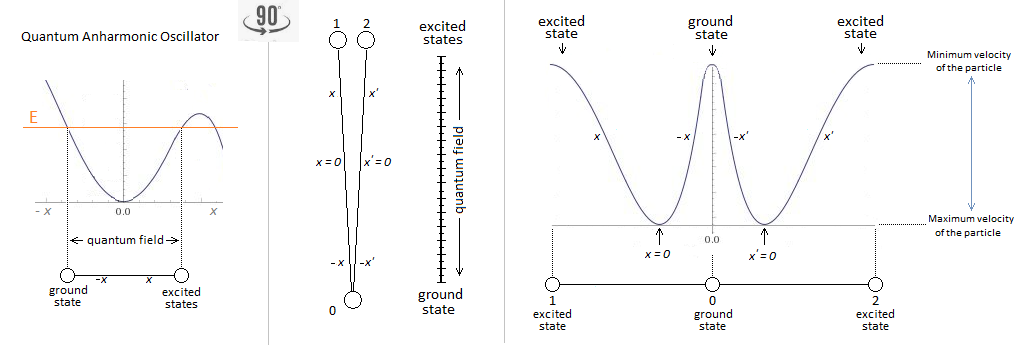
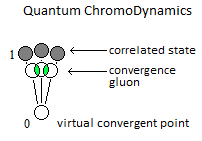
Is it possible that the origin of quantum chromodynamics, and at the level of strong interaction, is produced by the oscillation of a single particle in motion? This mechanism would use a principle of oscillation of the particle between a virtual convergent point and correlated quarks. I have already learned about this paper: Using the single quark transition model to predict nucleon resonance amplitudes

It's better if I get v = 1 (max speed at x = 0)

I confess that I do not understand what error of advice I have not followed.

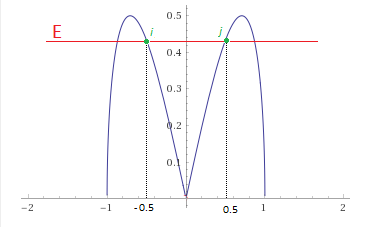
I do not know exactly. I think it's still at x = 0 that we have an equilibrium position. Otherwise I have this if x = 0 , v = 0 , a = 1 , b = 1 I know that I use a virtual oscillator that does not take into account Newton's laws with my plot. Afterwards, the race of the particle in the potential well is precisely related to the maximum energy. Now I know and in the case of a harmonic oscillator, and with the Newton's laws, that the potential energy is related to: \[ Ep(x)=\frac{1}{2}Kx^2 \] And in the case of an anharmonic oscillator: \[ Ep(x)=\frac{1}{2}Kx^2 - \frac{1}{3}AKx^3 \] But at the extremity of x (at i and j) there is also an equilibrium position that is created? No ? Where the particle slowed down to the max for after going back in the other direction.

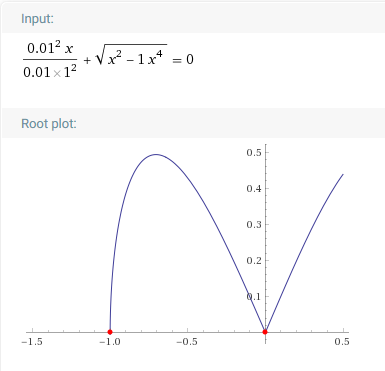
After several attempts I concluded that the value of b defines the size of the oscillator according to the total magnitude of x (several meters or a few millimeters), without losing the ratio of the proportionality between distance and speed and acceleration. I want to make big and / or small oscillator, I'm talking about the size of the length of x, the distance that separates the two ends of the particle. So I wish to change the equation, and rewrite it as follows: With a virtual particle and a virtual force, and if d is smaller or equal than to 0.01, can we define an oscillator like this? $$\frac{d^2 x}{dt^2}+\sqrt{x^2-bx^4}=0$$ If yes, can we compute v in the same way with: $$2\frac{{dx}}{{dt}}\frac{{{d^2}x}}{{d{t^2}}} = ...$$ Originally it was to find v we raised AKx³ to bx^4.

Yes thank you. In any case your help was precious to me. I thought that I can repeat the cycle with dx / dt where (t) follow x with a kind of table. The value of t gives the number of cycles. My question is: can I to write the initial conditions like that: 1 second = 1 complete cycle of x ? It's awesome this link, thanks again.

There is a maximum Velocity at x = 0. I understood. We can extend the y axis as much as we want. Which brings us to a sharp acceleration.

I did not understand the question. It is a particle that makes a round trip with the constraint of the contraction / relaxation of the spring.

Your plotting software looks really good. Thank you for that clarification. So, is it possible to insert a cusp parametric equation of the original equation? I think no, because I do not see how to reverse the tendency of y to -y without changing the original equation. I also thought of a partial differential equation (PDE), but I do not know if we can create a cusp with a PDE.

But apparently what I drew is always a cusp. So let's do it with a cusp. Within possible limits, how would the equation $$v = \sqrt {{{\left( {{v_0}} \right)}^2} - a{x^2} - \frac{1}{2}b{x^4}}$$ be with a cusp in addition, when x becomes x<-1 and x<1 ?

I have re-drawn the curve to avoid infinity.

Good evening studio. Let's say really fast, but not infinite, because if this velocity is infinite at x = 0 we can not have duly determined velocity. The particle moves according to x and goes from for example, from -0.01 to 0.01 quickly. On the x-axis -0.01 and 0.01 being determined velocities for the particle. So its acceleration and velocity is determined at x = 0 if the particle stay in passing half a nanosecond for example. How to go from a determined speed (-0.01 for x) to infinity (x = 0) and then return to a determined speed (0.01 for x)? If the velocity at x = 0 is infinite, or not, does this change the shape of the equation between the two choices?

I start from the principle where v0 is the velocity when x=0. But since I do not know much, we'll see. However I have another problem to raise. I know very well that a and b are constants. But it would be necessary for a to become a variable, or to use a second constant named e linked to a if a remains a constant. Indeed I wish to use these conditions in the equation: ax if x⩾1 ax if x⩾-1 and ex if x<1 ex if x<-1 This allows me to force the acceleration of the particle when x tends to 0. Here is the desired curve: I would like to keep the form of the equation except that when ax approaches ~1 (0.999...) for x, then the constant a changes its value (a becomes e) Maybe it should be two constants related to extrapolated values written as eax? Or is there another solution? Sorry for not being able to express myself better.

In this way $$ f(x) = \frac {1}{x} $$

I had warned that thread was going to be based on speculative. My only support is this one: https://www.scienceforums.net/topic/120416-anharmonic-oscillator/

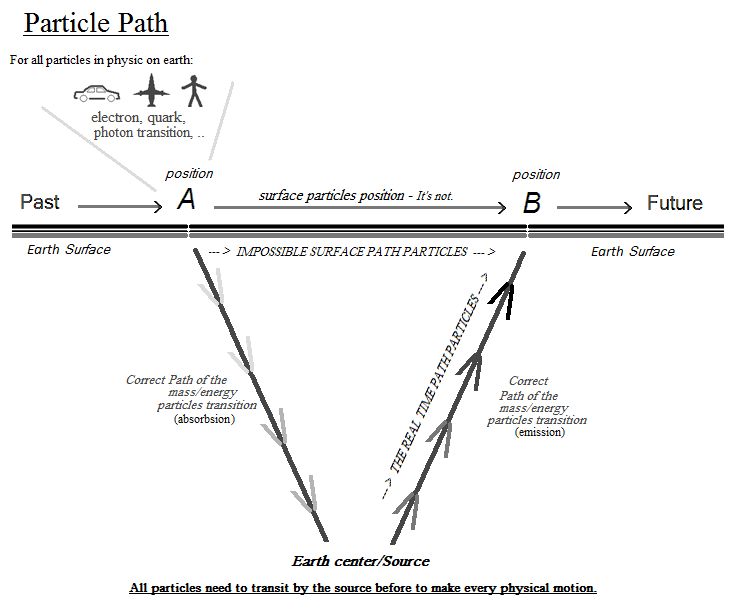
I did not know anything. It is the mechanics of the oscillator that brought me to this conclusion. The scope of gravity is infinite. So all the particles are there. But the question arises when an object leaves the earth. It can be relayed by another system, such as the sun. I also use this principle of oscillation between singularity and stars with the supermassive black holes and the galactic loop. In this case, and in between two, the flow of the particle becomes dark matter? In fact the real path of the prticule is this one: big-bang -> supermassive black hole -> star -> planet It's pure speculation but the sun is the point of origin of our solar system and manages all the objects that are there. The point of origin of the particle oscillating between sun and center of the earth. There should be a sunspot in the axis of every planet.

Yes. That's why I opened the Anharmonic Oscillator thread.

Yes I admit. I made a mistake by using the term singularity. Let's say rather a convergent point according to the terrestrial gravity field.

Yes A gravitational singularity. I do not see where the problem is.

This is the only solution to converge the information and the electrical charges of the system, and to regroup at one point the set of sequences of controlled oscillations. I simply associated the acceleration of the particle to mass in eV. My model defines the type of particle when it is at rest, because the oscillator gives the particle a total stop of its movement in time with a very short life span. A singularity of transition and gravitation.

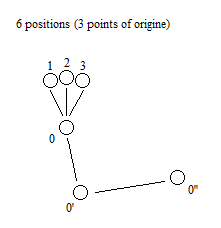
Yes I know. But I still try to make an approach as such. The single particle atom is radiative. Indeed, its oscillation is along an axis, and not a circle or sphere as orbital. Radiation can propagate between the points A->B A->B' A->B'' A->B''' for example. But I will think about it. How can we know it? In addition, the singularity of which I speak is that of the center of the earth for example. A perpetual oscillation of the particle between the center of the earth and the atom. Indeed this is problematic. But in my case the electron becomes more massive when it dissociates from its orbit and become as heavy as a proton. rather as heavy as a quark.

Hello This thread is pure speculation of an unknown physics phenomenon (optical illusion type). I do not expect any answer or help, because all this should remain for the moment incomprehensible of all. I created only this thread for archive and continuation if there will be. Thank you. The atomic model described in this thread represents the synopsis of the logical sequence of the oscillation mechanism of a single moving particle. Reference: https://www.scienceforums.net/topic/120416-anharmonic-oscillator/ I - Anharmonic Oscillator Here is the diagram of the anharmonic feature of the particle. Its oscillation is between singularity and visible matter, where between two its acceleration would be almost infinite. Here is the diagram of the path taken by the particle in the oscillator, as well as the role of the particle in the representation of the atom: Example of an atomic particle according to its delivered energy: II – Quantum atom The quantum atom is basically composed of quantum jump method of the particle, between singularity and correlation of the mass. These jumps correspond to the Bottom-up oscillation and are of almost instant value. They can be of the order of a few million jumps in a nanosecond. The exclusion of Pauli is respected because there is only one particle present per atom created by reiteration. Pure quantum atom, and series reiteration of Neutrons Protons (same number of N than of P): Isotope-type quantum atom and NPN reiteration: Quantum atom composed by NP and NPN reiteration: Thanks to the principle of reiteration, the probability of finding after NP and NPN in the atomic nuclei is consequent. Which brings us, and in relation to the atomic signature, to the conclusion of a composition rich in Deuterium, Tritium and Helium 4-5-6 The atomic signature corresponds to the spacing of the lines according to the energy delivered from the particle. The smaller the energy in ev, the greater the spacing of the line. The absence of line indicates that there is no particle in the field to study. Each line represents the path to the singularity that could be responsible for the electrical charges generated.

I know I was wrong. Because C is different of √C. So if v²=C when x=0 then √C also gives the root for x is √x I only know f(x) and I understand for the time being the infinitesimal interval of dx/dt. I have not yet understood v0. Maybe you would have a link that explains it?