Kartazion

Curvature occurs only by under the influence of mass or energy. Mass being that represented at rest in Figure 3 is then substituted by energy. The curvature is therefore produced by this energy distribution. For example for inflation similarities are to be noted between the shape of the charge/discharge curve of an RC circuit through Vc.

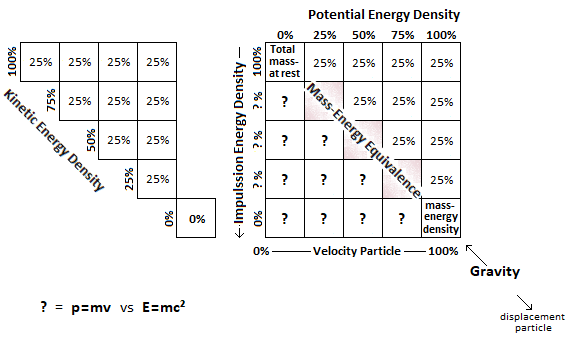
The ratio between the "impulssion energy" and the velocity of the particle gives the curvature by "?". Dark energy can maintain constant or accelerated kinetics. But in the fugure case presented the particle has reached the end of the expansion of the universe and falls back into a big-crunch.

Here in Figure 3 is an archaic representation, really very basic and non-operational yet, but which already gives an idea of how one could interpret the flow/flux of mass-energy equivalence related to the impulssion/momentum energy ; And integrated into the gravitational attraction. A clear distinction must be made between the mass-energy equivalence and the momentum energy given to the particle. The depletion of momentum energy occurs as the particle picks up speed. IOW the exhaustion of the energy of the impulssion is related (proportinnal?) to the speed of the particle. I have to complete the missing parameters. I'm working on it. Your help has been invaluable to me. I'm not sure I have correctly identified the problem in relation to the tool called energy–momentum tensor or else it represents a different vision. Figure 3.

Tweaking. Sorry. 'pofinage' was a French word. I wrote orthonormal and not orthogonal. A gravitational singularity is a region of spacetime in the vicinity of which certain quantities describing the gravitational field become infinite regardless of the coordinate system used. The Kerr metric is also a vacuum solution and describes a black hole and the shape of a ring can be called a ring singularity or ringularity. I corrected. Thanks. I don't want to be clumsy in my answer. But already the mass of the particle at rest located at the level of the singularity represents the total mass of the universe. I therefore let you imagine the amount of energy to be applied to the particle in order to be able to simulate inflation through an oscillating movement.

I don't know yet demonstrated a metric tensor. But the metric (maybe the term is badly chosen) in the proper sense of the term does not change the orthonormal basis. On the other hand, the interpretation of the curvature of space-time of the black hole is affected by the innovation that I support. To do this, and at first, a simple matrix can be used. But I haven't finished writing about it yet. I already have all the technical elements but the pofinage remains to be determined. This remains a complex subject in its interpretation of what is a space-time curvature from the inflation. In a second time the tensor will be able to generate the shape of our universe in its continuum, while the matrix will be the mechanism which constitutes it through the particle.

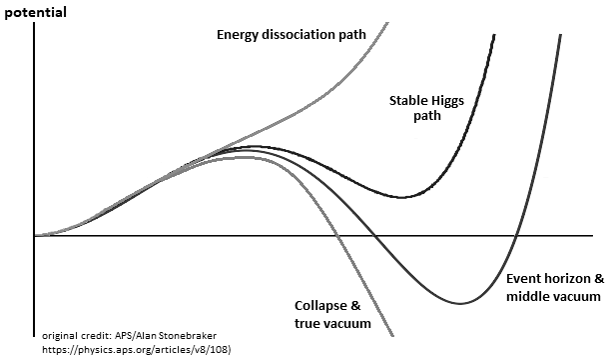
Yes of course. It corresponds to the particle at rest of an immeasurable value of its mass, and as well as the interpretation of the true vacuum in quantum field theory. Thereafter the extension of the particle is interpreted by the principle of mass-energy equivalence. The purpose of this experiment is to be able to precisely add the explanation of inflation up to the Friedmann-Robertson-Walker metric which is already very good one. The problem with Kerr–Newman metric is the consideration of symmetric entailment. But Newman found a way out with Axial symmetry. In this reference I base myself on an energy density of the particle as a convergent point thanks to the principle of mass-energy equivalence, until its rest: IOW Kerr-Newman metric describes a black hole solutions to the Einstein-Maxwell equations of general relativity. Very simply and for a black hole considering a potential energy and a kinetic energy of the particle by Hawking radiation determines the following clock Figure 2. Figure 2.

Hello. I indeed have a preference for the interpretation for Kerr–Newman metric which seems to me the one that comes closest to the gravitational singularity, because this metric includes the non-zero mass with a non-zero electric charge and an equally non-zero angular momentum. But I believe that its metric is limited to that of the black hole and does not assume the rest of the space-time to be studied. I will therefore open a new thread to explain if you will the metric which I think could elucidate the interpretation of the gravitational singularity of the big-bang type followed by its metric of expansion of the rest of the space-time of the universe . I don't know if I'm overdoing it but its name is Kartazion Metrics.

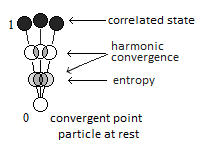
Hello. Here is a topic which is not one of the simplest. Here is the proposal for a new metric which has the principle of being able to take into account cosmic inflation in relation to the expansion of the universe. Indeed its mechanism is that of the interpretation and for a gravitational singularity of a single-particle entropic convergence. IOW what is defined as a singularity with infinite value would then only be an interpretation of a paricle at rest. The expansion of the particle from its singular point which expresses its rest will therefore propagate asymmetrically in space-time. At first, the entropy of a supermassive black hole is only the particle's alternation between singularity (singular point) and the galactic halo. When the correlated particle explained by chromodynamics, is expressed in mass, while its flow between singularity and correlated matter is expressed in energy by the prince of mass-energy equvalence (Figure 1). The next post will be fed with a more explicit explanation. Figure 1 Reference: [1] Kerr–Newman metric [2] Friedmann-Robertson-Walker

As you know I like to speak in pictures. Judging by my very first thread [1] on this form, here Figure 1 is how precisely the quasilocal mass is already an excellent visual approach to what I was saying previously. The second interpretation to be made and for the other part not understandable is simply appliclabe to the principle of the mass-energy equivalence. Figure 1. source: https://www.scirp.org/journal/paperinformation.aspx?paperid=116396 credit: https://orcid.org/0000-0001-7277-1654 [1] Yes yes. I understand where the community struggles to understand.

The fact that the gravitational waves are spiral indicates in one, that its propagation is asymmetric (outside the binary system), and in two that there is the possibility of being able to interpret the spiral propagation by an interpretation of a linear propagation mechanism (like a kind screw where its position on it is linear). But the more important is the interpretation of gravity as we know it, at the level of the observer, and in its "usual" interaction, acts as a vectorial action, and this attraction due to gravity is therefore perpendicular to the observer and this in relation to the ground i.e. here on Earth. IOW the radius whose source of gravity which is the emitter of it, crosses the gravitational wave by cutting it. I have a clear mechanical interpretation on this subject, but due to the rules of this forum I should open a new thread on it.

Ok. So what does this article brings to the understanding of the energies of the universe?

No it's not ambiguous. For example associate the linear displacement of the particle following the rotation of a clock which makes it possible to determine the position of the particle. In this example the direction stay the same and does not depend on the angle. IOW I find it logical and for angular rotation associated with the linear displacement of the particle, namely the speed of the particle according to the angular velocity to be able to determine its mass by mass-energy equivalence. A weak rotation of the angular velocity makes it possible to make move the particle radiatively or linearly in a form of classical interpretation of the mass, whereas a fast rotation determines a flow of it due to the principle of equivalence. Hence the angular momentum related to that of the mass of a black hole is fully justified.

I'm curious to know what the news is on this. If there is a source it is welcome.

It's something about Klein–Gordon equation. I thought it was used. Energy and flux is a scalar quantity. That's why I thought that.

But the interpretation of the energy E is scalar through the stress-energy-momentum tensor. It's just for confirmation. Thanks.

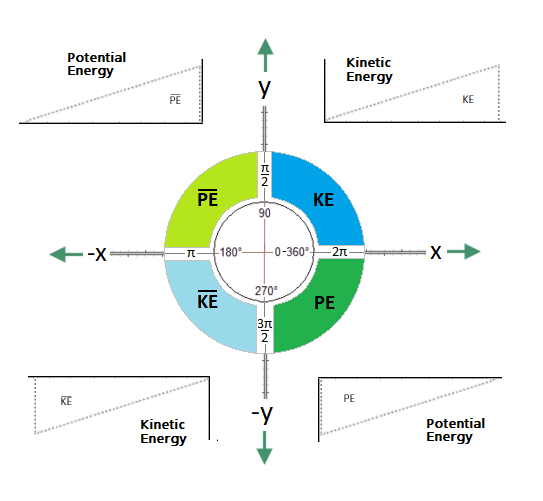
@Bufofrog I have answered your question 2 or 3 times. I told you that for the Y-axis it was the potential and this potential is that of energy. During inflation there are quantum fluctuations in the inflaton field. Since the total energy density of the universe is dominated by the inflaton potential energy density, fluctuations in the inflaton field lead to fluctuations in the energy density. Source: https://ned.ipac.caltech.edu/level5/Kolb/Kolb3_1.html For the X-axis. No it is not the radius. In general relativity and cosmology, the Hubble radius corresponds to the length scale characteristic of the observable portion of an expanding universe. In other words, the size of the observable universe is of the same order of magnitude as the Hubble radius. In fact the X-axis corresponds to the displacement of the particle. But you must understand that during inflation the particle remains immovable in relation to X and evolves only according to Y-axis by its momentum. Quantum fluctuations in relation to the inflaton and if we could, are not observable by its particle size but just by a set of a cluster. Am I wrong? Because I could also be wrong, or it's just you that don't understand how the inflation is interpreted in its potential well?

This is expressed in relation to the potential often denoted v. https://ned.ipac.caltech.edu/level5/Liddle/Liddle5_1.html One can think of the first term in each as a kinetic energy, and the second as a potential energy. The potential energy V() can be thought of as a form of `configurational' or `binding' energy; it measures how much internal energy is associated with a particular field value. Normally, like all systems, scalar fields try to minimize this energy; however, a crucial ingredient which allows inflation is that scalar fields are not always very efficient at reaching this minimum energy state. Note in passing that a scalar field cannot in general be described by an equation of state; there is no unique value of p that can be associated with a given as the energy density can be divided between potential and kinetic energy in different ways. In a given theory, there would be a specific form for the potential V(), at least up to some parameters which one could hope to measure (such as the effective mass and interaction strength of the scalar field). However, we are not presently in a position where there is a well established fundamental theory that one can use, so, in the absence of such a theory, inflation workers tend to regard V() as a function to be chosen arbitrarily, with different choices corresponding to different models of inflation (of which there are many). Some example potentials are (35) (36) (37) The strength of this approach is that it seems possible to capture many of the crucial properties of inflation by looking at some simple potentials; one is looking for results which will still hold when more `realistic' potentials are chosen. Figure 3 shows such a generic potential, with the scalar field displaced from the minimum and trying to reach it.

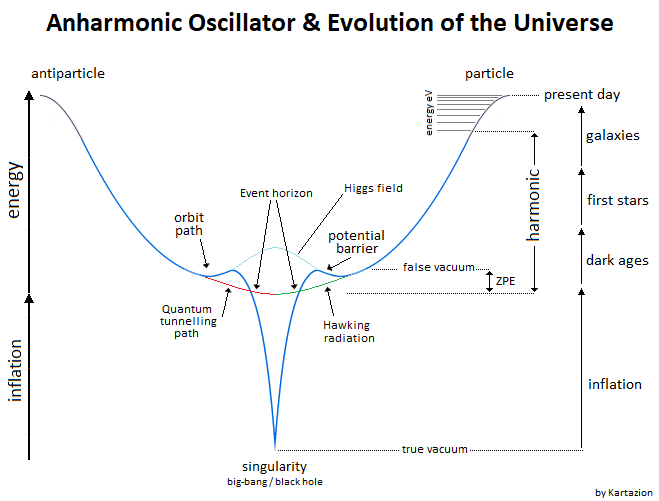
The symmetry breaking is located at x=0 at the level of the gravitational singularity. The charge and the parity CP are inverted between matter and antimatter. CP-symmetry states that the laws of physics should be the same if a particle is interchanged with its antiparticle (C-symmetry) while its spatial coordinates are inverted ("mirror" or P-symmetry). The oscillation of the particle between matter and antimatter gives the characteristic of an asymmetric distribution.

Yes exactly. This is inflation through the gravitational singularity energy potential. Of course the energy is that of potential through its density. https://universe-review.ca/R02-13-inflation.htm https://ppt-online.org/180450

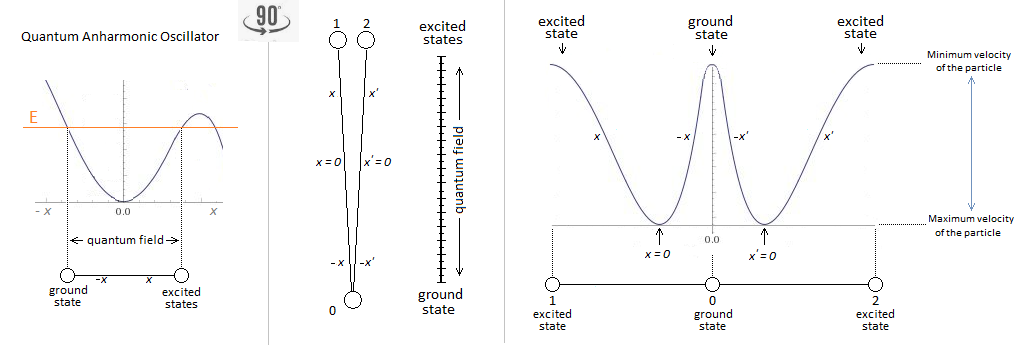
It represents the evolution of the universe through the anharmonic oscillator. https://medium.com/predict/the-oscillating-universe-d259ab408433 To who? You are in the denial of reality. https://arxiv.org/abs/astro-ph/9904313 In a recent paper Damour and Mukhanov describe a scenario where inflation may continue during the oscillatory phase. This effect is possible because the scalar field spends a significant fraction of each period of oscillation on the upper part of the potential. Such additional period of inflation could push perturbations after the slow roll regime to observable scales.

Okay. Well done. But coming from me you've never seen it before. By ambiguity this brought confusion for the reader of a fact that this graph already existed. But it's not. On the contrary, dear friend. We must already begin with the beginning. But ok it is the gravitational singularity of the Big-Bang which allows to develop the energy of current potential energy of the universe. So?

Everyone knows you're unable to provide a source for what you're saying. You put yourself in a very awkward position. Now I'm waiting to see what you're going to answer me. I can easily explain each of these points. I start with the simplest with the example relates to the "Hole Through the Earth Simple Harmonic Motion". The functioning of our universe and atomic is based on the oscillation of the particle itself and asymmetrically between matter and antimatter. This mechanism is a classical an-harmonic oscillator and uses a linear oscillation of the particle, where the energy can be represented by the graph of a potential well followed by the principle and law of conservation of energy between the kinetic energy and potential energy. This an-harmonic oscillation therefore occurs with a gravitational oscillator (see "Hole Through the Earth Simple Harmonic Motion"). This linear gravitational oscillator in the following figure uses a particle of mass m oscillating vertically along the gravity vector G. The oscillation has two phases. The first is the falling phase of the particle with its Potential Energy PE and the second is the reverse phase which corresponds to the Kinetic Energy KE. It is from the center of the Earth that what is in Potential Energy is transformed into Kinetic Energy and is reversed at the level at the point of origine 0 or x=0. Potential Energy - Kinetic Energy = 0 References: 1. John. D. Barrow; Mariusz. P. Dabrowski; Oscillating universes. Monthly Notices of the Royal Astro nomical Society 1995, 275, 850-862, 10.1093/mnras/275.3.850. [82] [83] [84] 2. Yun-Song Piao; Yuan-Zhong Zhang; Inflation in oscillating universe. Nuclear Physics B 2005, 725 , 265-274, 10.1016/j.nuclphysb.2005.07.021. 3. Itzhak Goldman; Nathan Rosen; Gravitation Theory and Oscillating Universe. Physical Review D 1972, 5, 1285-1287, 10.1103/physrevd.5.1285. 4. Roy A. Briere; LHCb Collaboration; Observing Matter-Antimatter Oscillations. Physics 2013, 6, 1- 3, 10.1103/physics.6.26. 5. M.K. Parida; Natural mass scales for observable matter-antimatter oscillations in SO(10). Physics Letters B 1983, 126, 220-224, 10.1016/0370-2693(83)90594-4 9. Andrew J. Simoson; Falling down a Hole through the Earth. Mathematics Magazine 2004, 77, 17 1, 10.2307/3219113. 10. Journey through the center of the Earth . Hyperphysics. Retrieved 2022-7-28

Hello, Here are in pictures of the evolution of the universe as you've probably never seen it. References: