wtf

I feel like I've been here before ...

The claim that every even number is the sum of two primes is the famous Goldbach conjecture. It's an open problem. https://en.wikipedia.org/wiki/Goldbach's_conjecture If you have a proof that Collatz depends on Goldbach that in itself would be valuable. I would say it's unlikely you have such a proof but if you do you'll get famous, even without solving Collatz.

I hope this isn't going to be one of those probabalistic arguments. Half the integers are even, half are odd. If you pick an even n you make it n/2. If you pick an odd n you make it 3n + 1, then since that number is even on the next step you make it (3/2)n + 1/2. So over time you're multiplying by 3/2 and dividing by 2. The limit goes to 0 therefore all numbers eventually go to 1. This is a fairly common false proof. You have to prove it for all n, not just the behavior of n in the limit. I've seen more than one version of this over the years.

> I need to generalize my <* ordering. It needs to be an ordering on the whole set R because it has to be the possibility of any ordering. What does that mean, it has to be the "possibility of any ordering?" It's not even clear what you are trying to do. In order to make progress my suggestion to you would be to force yourself to write more clearly, one line at a time, and make sure each line makes sense. You don't have to write here, do it for yourself. Your ideas are jumbled because your prose is jumbled. That's why they make you write proofs in math class. Clear exposition leads to clear thinking. > wtf, do you mean that Cantor rational number thing? Yes, the fact that the natural numbers can be placed into bijection with the rationals. > I dont know why u asked this. Because you have to walk before you can run. You are trying to investigate or understand the relation between the usual dense order on the reals, with the well-order on the reals. Now the reals are a very complicated set. There is a much simpler set we have lying around that has the same phenomenon. You should study it to try to gain insight into the analogous problem in the reals Specifically, the usual order on the rationals is dense, just like the usual order on the reals is dense. Now you want to find a well-order. We know we can re-order the rationals so that they are well-ordered. This is a perfect analogy for what you are trying to do. That's why I suggested that you study it. It's so you can gain insight into the analogous problem for the reals: How to relate a well-order to a dense order on the same set. It's a standard technique in math, when you are working on a hard problem, to look at simpler examples. > I was going to show what I think is a way to reorder any set of real numbers in a dense or çontinuous way But why? Isn't the usual order already dense or continuous? You don't have to work very hard to find a dense order on the reals, the usual order is dense. > Im going to take a break from this now.This kinda gets to me after a while. I hope you got your money's worth from the convo. You should definitely take another run at learning about the ordinals. The ordinals are all about well-ordered sets. If you are interested in well-orders you are by definition interested in the ordinal numbers, even if you don't know it. I'll check this site from time to time in case you have more questions or comments. All the best, nice chatting with you. By the way I have a really cool book recommendation for you. Infinity and the Mind by Rudy Rucker. https://www.amazon.com/Infinity-Mind-Philosophy-Infinite-Princeton/dp/0691121273

Here's another example you should be thinking of. We know that there's a bijection between the naturals N and the rationals Q. The usual order on Q is dense and the usual order on N is a well-order. You should try to run your ideas through this example since it's a countable and well-understood parallel to the case of a well-order on the reals versus the usual dense order.

Just because t < a, why should we still have t <* a?

Just because t < a, why should we still have t <* a?

Run your argument on the naturals ordered by the usual <. Is there such a subset S?

I say again: Please state in one sentence what you are trying to claim or show. * You agree what AC implies the well-ordering theorem. * You seem to understand that even in the absence of AC, the reals might still be well-ordered. You keep diving into your argument without saying in one clear sentence what it is you are trying to show.

> Back in the 1980s I showed what I thought was a WO of [0,1] to a math prof at the Univ of Denver. He walked over to his blackboard, picked up a piece of chalk, thought for a few seconds and wrote out two infinite strings of numbers and asked me which one was greater with my order. I said uh oh and left. At least he didn't call your idea a trainwreck! Much nicer individual than me > A possible flaw in my hypothetical ordering is that I might be thinking of it in a usual sense. But, there just seems to be no other way. Any way you look at it you run into infinity somewhere. Again, I say all I need to do is show there is one subset that no l.e. can be found with the assumed WO to prove my assertion. I don't understand your assertion. Can you write it down clearly in one sentence? Are you saying no well-order of the reals exists even in in the presence of AC? That's false. Are you saying no well-order of the reals exists in the absence of AC? That might be false too. You seem to understand both these points. So I don't understand what you are trying to prove or what you are claiming.

> I hope he will post something for me. That's a very kind thing to say. I agree that I deliver criticisms that could be taken personally, but they are not intended like that. When I say your argument is a trainwreck, that's a statement of objective fact based on considerable experience with proofs in this particular area of math. If I'm your TA I'd write "trainwreck" in big red letters. My intention is to be of assistance to you in understanding these ideas and learning to express your mathematical ideas more effectively, if that's your desire. To do that a certain level of precision is needed, both in concept and exposition. And I'll call you on lack of same. > Then wtf tells me I proved my assertion for dense sets and nothing else. If my proof is valid for these why does it not prove my assertiion? This makes no sense. Oh how funny. Yes I can see that you misunderstood this. I have a perfect explanation for you. I told you to carefully write out your proof that a dense linear order can't be a well-order, for the purpose of you getting practice in expressing your mathematical ideas and writing formal proofs. I reiterate that suggestion. I did not mean to imply that this would help your cause. We agree that it's not sufficient, because you still have all those OTHER linear orders that aren't dense but that might be well-orders. But you would learn a lot from struggling -- and yes it is a neverending struggle for ALL of us -- to force yourself to write math clearly. That is the only way to get better at it. I suggested this as an exercise. I hope that's not presumptuous in a message board format. I've been through this material and I've had proof-writing beaten into me by distinguished professors at some of the nation's finest universities. It's simply the only way to learn this stuff. If there were a pill we could take, we'd all take it. As Euclid said: There is no royal road to geometry. Even the King has to "do the math" if he wants to learn. > I guess the natural numbers being well ordered is supposed to contradicts my proof. You are asking why I talk about N. The reason is that they are the SIMPLEST example of an infinite well-ordered set. So when we're trying to get insight into a well-ordering of the reals, one place to look for intuition is in the much more familiar well-ordering of the naturals. And this is a math trick! Whenever you have convinced yourself that you proved something about a complicated object, run the proof on a simpler object that the proof still applies to. If you end up proving the naturals aren't well-ordered, then you know your proof's wrong. Re ordinals: Your interest in well-orders has led you back to the ordinal numbers. They are hard for everyone at first but they are one of the very coolest things I know about in math. They're well worth another run at that part of the book. By the way a well-order of the reals is an uncountable ordinal. That's a very strange beast to get one's mind around, it takes some work and study. So if you want to think about well-ordering the reals, you need to learn about ordinals and work your way up to the wild idea of an uncountable ordinal. The existence of an uncountable ordinal can be proved WITHOUT the axiom of choice. That is a very interesting fact I think. I can walk through the proof but you do need to believe in the ordinals first. > Iĺl get pushback from wtf for this. Didn't you initially ask for someone who knows this material? Be careful what you wish for > wtf mentioned other models of set theory that allow well ordering without the need of the AC. I truly want to see these. Yes this is not a hard reference. It's a mention of a fact that, once I thought about it, must be true. I found it in a very unlikely place, in the Talk page for the Wiki article on the Banach-Tarski paradox. Whenever I look at a Wiki page I often look at its Talk page, where the editors argue about what the article should say. You get a lot of insight from these sometimes. So, here is the Talk page for the Banach-Tarski paradox: https://en.wikipedia.org/wiki/Talk:Banach–Tarski_paradox And way down the page there is this conversation about how much Choice is needed. (Sometimes you don't need the full axiom of choice, you can get by with weaker principles like countable choice, dependent choice, and some other intermediate axioms.) Without going into this in detail -- readers can click if desired -- someone at some point said this: And it must have been known since the sixties that it's consistent with ZF that the reals can be wellordered but some larger set (say, the powerset of the reals) cannot. The moment I thought about this I saw it must be true. The well-ordering theorem says that ANY set can be well-ordered. Its negation says that SOME set can't be well-ordered. But it doesn't say anything about which set that is. So it must be logically consistent that the real numbers are well-ordered, yet some larger set isn't. In this particular model of set theory, well-ordering is false and the axiom of choice is false yet the reals are well-ordered. These are deep waters.

Are you talking about the proof that the reals are uncountable? Or that the unit interval can be placed into bijection with the unit square? It's the proof of the latter that you outlined.

Yes Cantor did this. See the section titled "Squared Infinities" here ... https://plus.maths.org/content/glimpse-cantors-paradise

> OK, I see what I did. That a set can be WO depends on the AC. The two are equivelent statements. The natural numbers are well-ordered in the absence of AC. And as I noted, even the real numbers might be well-ordered even in the absence of AC. What AC says is that EVERY set may be well ordered. > What I showed is WO does not exist naturally on its own. Its like saying if we can live on air we do not have to grow food and we know the first part is impossible. That doesn't make much sense. Even in the absence of AC, there's a model of set theory in which the reals are well-ordered. And without AC, plenty of sets are "naturally" well-ordered, like the natural numbers, or any finite set, or any of the transfinite ordinals. You certainly did NOT show that "WO does not exist naturally on its own." You didn't show anything like that. > What I did was just an exercise. You don't seem to have understood the flaws in your own thinking. You think you proved that "a WO does not naturally exist on its own." First that doesn't make sense, since you haven't defined your terms. And second, under any reasonable interpretation, it's false. > Of course something like this could never overturn 100 years of history. Of course it cannot be that simple. If a set is WO then there you have your set of numbers for the AC. No no no no no no no. Even in the absence of AC, all the ordinal numbers are well-ordered. And even in the absence of AC, the real numbers might be well-ordered. > Yes, its clear the natural numbers can be WO, but my thesis was that not every set can be WO. If you accept the AC then of course you say they can. "I say" they can? What do you say? You deny that AC implies that every set can be well-ordered? Your phrasings are so imprecise that they are causing your thinking to become confused.

@taeto has already addressed and falsified your latest idea. I'll just add that you can get some clarity by running your argument on the natural numbers {0, 1, 2, 3, ...}. The naturals are well-ordered and 0 is the first element. So let T = {1, 2, 3, 4, ...}; that is, the naturals with 0 removed. Now what is the least element of T? It's 1. That's how well-ordered sets work. Wouldn't your argument "show" that the naturals aren't well-ordered? As @taeto already asked, why do you think T doesn't have a least element? > Oh, and the Continuum Hypothesis is also in these equivallent statements. No no no. CH is independent of all of them. In fact if you assume CH you get a nice well-ordering of the reals that you can almost visualize. The first uncountable ordinal can be proved to exist even without AC. If CH is true, the first uncountable ordinal well-orders the reals. And with a bit of study, you can visualize the first uncountable ordinal. It's just the set of all possible well-orders of the naturals. Equivalently, the first uncountable ordinal is the set of all countable ordinals.

I ran across something that I didn't realize before, but it makes perfect sense. The well-ordering theorem is equivalent to AC. The well-ordering theorem says that ANY set can be well-ordered. That implies of course that the reals can be well-ordered. However, suppose we deny AC. Then there is SOME set that can't be well-ordered ... but it might not be the reals. That is: There is a model of set theory in which AC is false, and there is SOME set that can't be well-ordered, yet the real numbers are well-ordered! So I was wrong before when I said that you can deny AC and thereby prevent a well-order of the reals. On the contrary, the reals can be well-ordered (in some model of set theory) even in the absence of AC.

If you leave the thread as it is, someone curious about this subject might come by in a few years and learn something. I think your instinct was right. You did show that a dense order can't be well-ordered. The point wouldn't be to give up on your studies. The point would be to learn more. As I said, your instincts are good. I'm trying to encourage you to learn a little more, not to give up. Remember that when Wiles announced his celebrated proof of FLT, someone found a significant error in his work. It took Wiles over a year to patch the problem and get a completed proof. You did a good job. You had an insight, you proved something interesting, and you realized that you had a logic error. Wiles did the exact same thing! If you are rusty at math, well you are less rusty now than you were before. Keep at it and soon the rust will turn to shiny stainless steel.

> I gave an answer using a library computer and didn keep track of the time limit. It was completely lost. Iĺl have to do it again. Sorry to hear that. On the other hand it's been my longtime experience that whenever I write a lengthy screed and manage to lose it, my second effort always comes out much better. > Iḿ thinking Iḿ sticking to my original statements. But your original statement is wrong. You showed that no dense linear order can be a well order. But you didn't account for the case of some non-dense linear order. > As I said before if a order relation, <*, WOs the set of reals there has to be a l.e. according to <* in every possible subset of the reals. Every nonempty subset. Picky picky! > If every possible subset cannot be constructed there is no guarantee a subset made up of elements each from each subset of the reals exists either. The powerset axiom guarantees the existence of every subset of the reals. These subsets do not need to be "constructed," whatever you might mean by that. I do not have to explicitly exhibit each of the subset of the reals to know they exist. https://en.wikipedia.org/wiki/Axiom_of_power_set But you seem to be arguing against AC. That's pointless. You're perfectly free to adopt its negation, that gives a consistent set theory. There's no argument to be had. If you reject AC then well-ordering is false and we're done. You lose a lot of modern math and a good chunk of physics but you're not wrong. Only out of step with contemporary mathematical practice, which I perfectly well agree is historically contingent. > I like this Chromebook yes and no. There are a number of limitations, but its easy to carry anywhere. There is no delete' key.You have to use backspace. I think I finally found out how to disable this auto correct. I'll check it out. Google already owns my life anyway. Resistance is futile.

> Yes, it's inconceivable how a dense set can be turned into a 'discrete' set of numbers-what I was trying to depict there Well it's not a bad idea for the first try. But now we see there's no use even thinking about dense orders. They are not candidates for being a well-order or proving there isn't one. > I haven't found a way to stop this absurd autocorrect on this Chromebook either. Do you like your Chromebook? I need a new computing device and they look interesting. Then again do I really want to be even more tied in to Google? > On thinking of this more I concluded we could consider any subset whatever no matter the structure with <*. I'm afraid I don't know what you mean. Consider any subset of what, for what? Are you talking about the powerset of the reals, the set of all possible subsets of the reals? That's a big set. What does it have to do with you idea? You lost me here. Please me much more clear and specific. > Does that need to be proved or taken as an axiom?. Whatever it is you're talking about, you have not made it clear to me. "consider any subset whatever no matter the structure with <*" strikes me as meaningless. Can you please clarify what you are talking about? > Such a set I constructed doesn't have a l.e. I have no idea what set you've constructed or what you are talking about. The last time I looked, we had agreed that a dense linear order is not a candidate for being a well-order. Now whatever you are talking about makes no sense to me. I don't know what argument you're making or what you're trying to show. > But, guess what, saying any set can exists implies a set satisfying the AC exists. Any set can exist? What does that mean? And what is "a set satisfying the AC?" That also is inaccurate and murky. AC is a property about all collections of sets. A given set can't satisfy or not satisfy AC. Are you perhaps a little fuzzy on what AC actually is? > So, again this says the whole notion is undecideable. We already agree that AC is independent of the rest of math; but is universally accepted as one of the axioms of math on pragmatic grounds. I'm afraid this most recent post of yours does not make any sense to me at all. Please do clarify your idea, starting from the beginning and going step by step.

[Replying point by point by hand, since the forum software doesn't seem to allow interspersed replies. Is there a better way to do this?] > Well thanks, wtf. You're very welcome. > The real idea behind my effort is that I've always noticed that when you try to come up with a well ordering for the reals there is always a set who's definition is the very thing that violates the ordering. Yes perfectly well understood. You will never come up with a well-order of the reals and neither with anyone else. It's a consequence of the Axiom of Choice (AC), so it is inherently nonconstructive. There are models of set theory in which there is a definable well-order of the reals. There are also models in which there is no definable well-order of the reals. It's all a matter of highly technical set theory. For us mere mortals, it's enough to know that AC is logically equivalent to the well-ordering theorem, and we will never ever visualize or imagine a well-ordering of the reals. Now, perhaps we should reject AC. Because AC does imply some very weird things, like the Banach-Tarski paradox, the existence of nonmeasurable sets, and the Infinite Hat problem (if you haven't seen this it's a total mind-blower). https://en.wikipedia.org/wiki/Hat_puzzle#Countably_Infinite-Hat_Variant_without_Hearing So maybe we should reject AC. But there's a problem. The negation of AC also has a lot of bizarre consequences, like a vector space without a basis; an infinite set that's Dedekind-finite; and the nonexistence of the Cartesian product of a collection of nonempty sets. Since we're damned if we do and damned if we don't with respect to AC, mathematicians choose to adopt AC because it gives more ways to prove interesting theorems. This shows that mathematics is not about certainty. It's about historically contingent aesthetic choices as to what constitutes valid mathematics.Whenever we use AC we are right at the heart of the philosophy of math. In the end there's no right or wrong. AC is mainstream today. In the future, who knows how people will regard nonconstructive math. They might reject it entirely. > My use of intervals is not a good example. Let me see if I can come up with a construction that works. Let me try this: Suppose A has a l.e. a with respect to <*. Now comsider B=A\{a}. Then a is not the l.e. of B. Your WO hyp says B has a l.e. b and a<b since b is inA. A and B are dense so there exists an x such that a<x<b . x can't be in B..... Anyway, this all leads to a contradiction. Ok there's an awful lot of confusion to untangle. [I don't mean for that to sound personal in any way. I am only critiquing your argument you originally requested. I share your intuitive sense of all this. A well-order of the real numbers is absurd on its face. We're in perfect agreement on that. We're just at different stages of acceptance of nonconstructive math. It's a psychological process]. Let me say this to start. Dense orders and well-orders are mutually exclusive. If a total order is dense, it's not a well-order. And if it's a well-order, it's not dense. At some level I think that's where you're coming from. You're showing that a dense order can't be a well-order. Your proofs are inaccurate but your intuition is perfectly correct. You're then concluding that no total order can be a well-order. That doesn't follow. All you're proving is that a dense order can't be a well-order. That is true! Also the converse. No well-order can be a dense order. You might have a go at writing a formal proof of that. > I hope I don't sound like I'm going around in circles. I think your instinct is correct, that no dense order can be a well-order. Your proofs are muddled and you should think about how you could prove this. Your other issue is that you are concluding that NO total order can be a well-order. But all you've proved is that no DENSE order can be a well-order. That's true, but it doesn't preclude some non-dense order from being a well-order, and that's exactly what happens. > Yes, I need more thought on this; no doubt you'll tell me I need a lot more thought Thought and study. The trick is to learn to get very rigorous and picky with the symbols. By the way that's where LaTeX or MathJax comes in handy. I know how to copy and paste symbols, in fact http://math.typeit.org/ is one of my favorite sites. However, and just take this as a suggestion, if you are interested in studying math ongoing, you should take the trouble to learn LaTeX. It produces beautiful output and it's much easier to read than the copy/paste stuff. It's the default for all mathematical writing these days in those online venues that support it. > ....OK, now I think I know what you are saying: If any set is WO it is turned into the form a1.a2, a3, ..., but I'm saying for any WO there will always exist a set that can't be turned into this structure. Not actually following what you're saying here. But if you drop your belief that every linear order has a dense subset, you'll see that this is exactly the counterexample to your mental picture. A well-order is a linear order that has NO dense subset. You've actually given the proof. If x is the smallest element, then if you delete x there's no smallest element if the set was dense in the first place. So a well-order can have no dense subsets. You proved that! You know your mathematical sense is pretty good. You need to learn to do the formal symbolic part. That's what Real Analysis does. They run you through so many proofs that the symbology becomes second nature. If you're so inclined, you should methodically work through your book and do lots of exercises. > I realized I haven't really proven anything. You haven't proven your overall thesis that a well-ordering of the reals can't exist. But you have proved that a dense linear order can't be a well-order. That's a good thing to know. But what if there's some linear order that doesn't have a dense subset? That order is a candidate for our mythical well-order. You haven't covered that possibility. > While I believe any ordering can select a group of numbers it can't find a l.e. for I have to show just how this works. Not clear what this means. Well I wrote a lot of words, I hope some of it was helpful. I really encourage you to learn more real analysis and more set theory too. Feel free to ask questions.

There There are two related but different definitions of "dense," and completeness has NOTHING TO DO WITH EITHER. * A set is dense if there's a third (distinct) point between any two points. So the rationals are a dense set and so are the reals. * A set X is dense in a set Y if every element of Y has elements of X arbitrarily close to it. For example the rationals are dense in the reals. * A Cauchy sequence is a sequence that should "morally" converge. For example the sequence 1/2, 1/3, 1/4, 1/5, ... should converge, and in the real numbers it does, to 0. But in the open unit interval (0,1), it does NOT converge, because there's nothing for it to converge to. Its limit, namely 0, isn't in the set. * A set is complete if every Cauchy sequence converges. The real numbers are complete, the unit interval [0,1] is complete, and the half-open unit interval (0,1] isn't. Note that completeness is a metric property and not a topological one. The open unit interval (0,1) and the real numbers are homeomorphic, that means they are identical topologically. But the reals are complete and (0,1) isn't. These are all perfectly standard definitions and any book on real analysis will define them the same way. Your posted proof is a train wreck full of misunderstandings and logic errors. Also, I'll assume you meant to say, "Thank you wtf for putting some effort into this to help me when nobody else in the world did" but simply forgot because you're so busy with other important things. ps -- Your approach is hopeless, by the way. Well-ordering has NOTHING to do with denseness or completeness. A well-ordered set looks discrete. It's got a first element, a second, a third, etc. A well-order can't be dense, because for example there are no integers between 2 and 3. In a well-ordered set, given any element there's a successor, with no other element between them. So your approach simply can't work. Likewise, completeness can't work either, since it's based on a metric, and most well-ordered sets have no metric defined on them. For example any transfinite ordinal number is well-ordered, but there's no metric defined on it. So the concepts you're using to attack the problem are the wrong tools. I do encourage you to learn more real analysis, it's a wonderfully interesting subject that will forever clarify your understanding of the real numbers. But flailing away with half-understood and misunderstood concepts, in order to disprove a standard theorem that's already been proven and accepted as true for well over a century, is not the most productive way to go about learning.

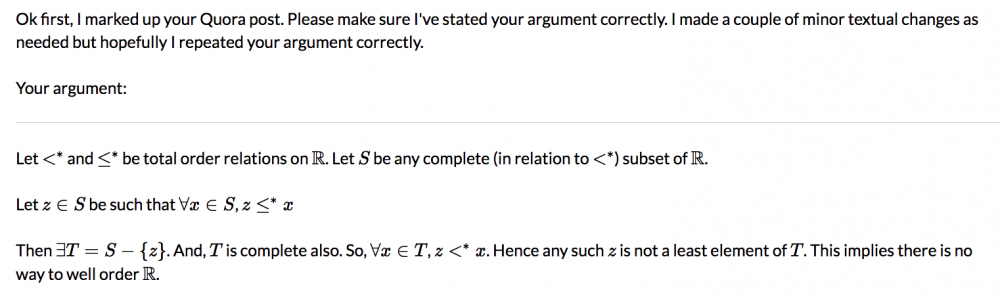
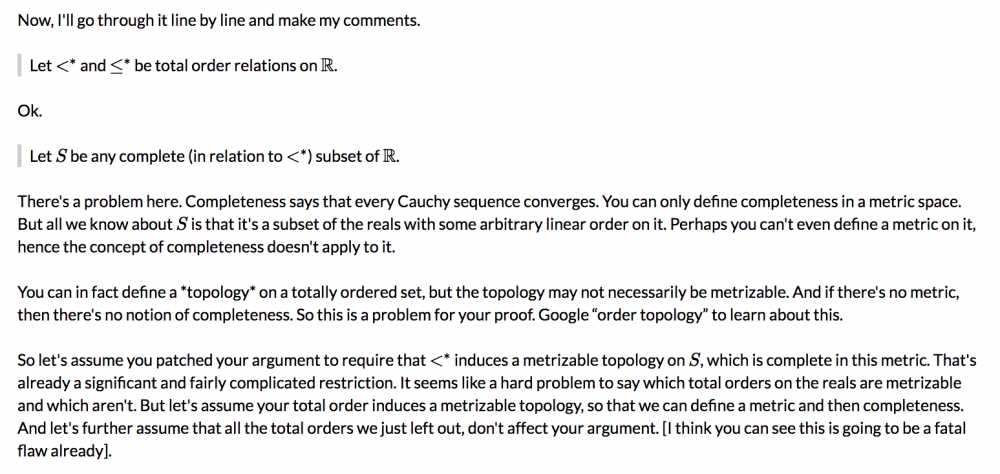
I found your Quora post here. https://www.quora.com/Where-is-my-flaw-in-thinking Here is the copy/paste for the benefit of readers keeping score at home. ======= let <* and ≤* be total order relations on ℝ. Let S be any complete (in relation to <*) subset of ℝ , let z ε S such that z ≤* x ∀x ε S. Then ∃T = S - {z}. And, T is complete also. So, ∀x ε T, z <* x. Hence any such z is not a least element of T. This implies there is no way to Well Order ℝ This shows for any possible well ordering of ℝ there still exists subsets of ℝ such that they have no least element in relation to the ordering. ======= I found two substantive and fatal errors. One, how do you define completeness for an arbitrary total order? Completeness is defined in terms of Cauchy sequences, and Cauchy sequences depend on a metric. If you are only given a total order, you can induce a topology on that order, called the order topology. https://en.wikipedia.org/wiki/Order_topology But the order topology may or may not be metrizable. If it's not, then you can't define a metric and then you can't define completeness. Secondly, just consider S = [0,1] in the reals with the usual order. Then z = 0 and all you're doing is showing that 0 is not in (0,1]. And in this case your T is not complete. I wrote a detailed, marked-up response. Evidently this site no longer supports MathJax. so I'll just upload some screenshots of my marked up doc. If you have any comments or questions let me know, but I'm not going to do any more screen shotting for this. Perhaps post this on a MathJax-friendly forum. If this site does support MathJax but I just couldn't figure it out, my apologies to the moderators.

I found an old post saying that MathJax is enabled using the ∑ button in the Edit window. But this button doesn't seem to be there.

Well, who would benefit here? You want someone who knows this material to critique your proof. I don't need to see your proof to know it's wrong. I sketched the standard proof and your comment is that AC "troubles" you. Whatever. If you deny AC you lose the well-ordering theorem and you're free to do that. Of course then you'll have a vector space without a basis, a set that's infinite yet Dedekind-finite, and you'll lose all of probability theory. A small price to pay for your "trouble." ZF minus Choice is perfectly consistent (if ZF is). So you have every right to adopt it as your personal axiom system. You're the one wanting assistance from someone who knows this material. Do you have something substantive to say or do you just want to jerk people around? I did search Quora and couldn't find your question, which you didn't bother to link. You won't get any more responses from me until you say something interesting.

Without looking it up, can you state the Hodge conjecture and explain in your own words what it means? Heck I'll make it easier. Go ahead and look it up and then explain to us in your own worlds what it means!