-
Posts
446 -
Joined
-
Last visited
-
Days Won
1
Content Type
Profiles
Forums
Events
Everything posted by Trurl
-
You are right 10^37 is too small. But the computation is fixable. The equation only used 75 digits of a 617 digit number. It can be corrected.
-
I watched a show that said, “We have time so everything doesn’t happen at once.”
But if there is a multiverse where indeed every possibility is happening all at once then our entire life and existence would be how we viewed the multiverse?
I have read a book called The Planiverse. It is about the discovery of a 2D universe. There is much science explaining this 2D universe. But more important than the physics is how the life forms experience life with their world.
That is my profound thought of the day. RSA is no more.
-
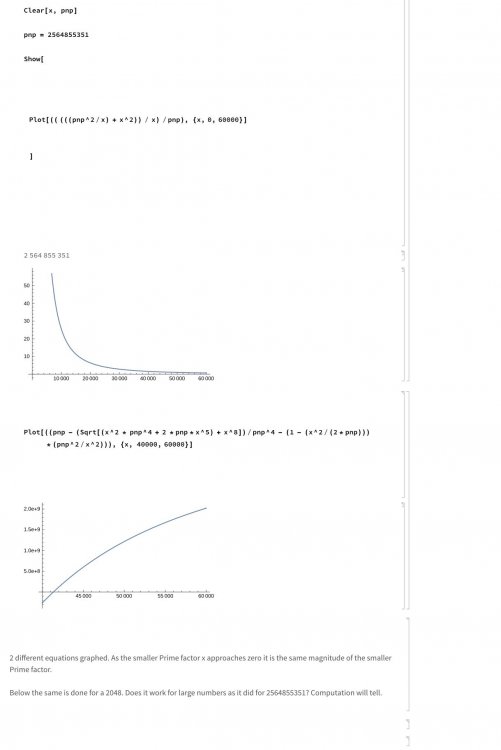
I will research how they are factored. But I did not do research, only original research. I haven't looked at it yet, but those mathematicians at Stanford are above me. It would probably take months to understand them. And are they correct. I will research them. Thank you for the link. I would say the problem with my numbers is that I was only factoring the first 75 digits. Computation gets confusing when the numbers get large. I would say to you on the code I have just posted below in this thread, "Prove it Wrong." Just as I have to prove it right, to me the numbers seem to be working. You could say the first number was wrong, but I don't think it is. My hunch is that you thought the magnitude of the smaller factor I proposed was too small. If there was an algebraic run to multiply a^n and b^m factoring would be much easier. But as far as I know no such rule exists. Read this code I post. I don't know the answer. I don't think anyone can say an answer. This is the distraction of my equations. But if they work it would change how we think about Prime numbers. Clear[x,y,g,pnp] pnp=2519590847565789349402718324004839857142928212620403202777713783604366202070\7595556264018525880784406918290641249515082189298559149176184502808489120072\8449926873928072877767359714183472702618963750149718246911650776133798590957\0009733045974880842840179742910064245869181719511874612151517265463228221686\9987549182422433637259085141865462043576798423387184774447920739934236584823\8242811981638150106748104516603773060562016196762561338441436038339044149526\3443219011465754445417842402092461651572335077870774981712577246796292638635\6373289912154831438167899885040445364023527381951378636564391212010397122822\120720357; x=40861574600078048833983218761558688141 y=(((pnp^2/x)+x^2)/pnp) 40861574600078048833983218761558688141 634833803913729274149046560006110105341653987032644347139491065463960765590983014594270745280490943612524425735691584192357714405134539298334254086508463781769463545365966990230877020139587494264115931259401035776266879854280637911181600802763300680148655445534314280852835966547981430518726074134498756877075347610533912610882082571593792533386863778600058303720971034349799390014347520048267237872419333149303301358190482052097820150373855848496280186985832493081485651076553227345540702399208519938470313956044554498336151298425477716733509134466593458008908417427074091201531204090188340432250521346783546450569186626944925787846341539066839302955697556953200935562068268509147390847569567813190953745889578796065991456608595094775372274724035820106046753346703202092454091532620276574400974810603033731667772333116072331674764649360687392789065558184319741482042496890297790135396659502960271951214593374229349810409021779095513702571776210723562008955029462000296608359090753780513193581054298210353890469163174127612293185453114099745606391072987998065659734323866602790265365503491919975152225157252257325443440549579867786230870245990843625165669247214878065515035182695333007699122793085682845204420142443354543637937394670/1029544493794833810362719399813336867927292796870105985767066638600787949056122326854257679972284970010944308811790024149299718090777560077453412457010521445303837785995429144256429395104047108858051197839406607192157326592513109026780645546804565855787882246931691946026121697600798370743023310919920240496366458210984067304416868633515308096356298816579415040357140823932519476960953659465709561744424103986576674496903092964092709805027103183570967574475083485410490451939386941577863721438385490436407675487353298659477292651598896919377654472607793847335861184927553234887906511137785877776276042420931844038131417543652262939192664076316610833186337 N[y] 6.166161906939770 × 10^578 x*y N[%131] 2.519590847565789 × 10^616 Still working. Let me know what you think. I will have access to the Wolfram files ready soon.
-
@Ghideon I need more hints unless you are saying the number isn’t Prime. If it isn’t Prime it would be close to the actual Prime. I know 38 digits does seem small divided into a 618 digit number. But as I have shown 2 of my equations point to it. So far no one knows what it is. The equations work for 2564855351. Maybe they will work for larger numbers. I’m interested in seeing how you proved it wrong. Right now I have no way of knowing but division.
-

Need to edit post. It posted multiple times.
Trurl replied to Trurl's topic in Suggestions, Comments and Support
Thank you Swansont for the quick fix.😀 -
My guess is that you proved my “suggested factor” not to be prime by factoring the “suggested factor.” That is ok because my factor is of the right magnitude. That is if my equations work for large numbers. As the graph approaches zero x approaches the smaller Prime number (in theory). I think I know one more way to test so give me until I post again before you reveal your method. It is late and I need more time to respond.
-
Read into it a little more. I am not saying that just because Einstein is a just man he is a Christian. I am saying how he changed the world and his attitude towards life reads like a character out of the Bible. He warns of the dangers of nuclear fission, he runs from the Nazis, he reveals wonders of the physical world, he tries to relate the physical world to the spiritual world, and he is a role model, and he respects everyone’s beliefs and unites people. it may not be that he excepted Jesus into his life, but given the right arguments I don’t think he would completely dismiss it. He wasn’t perfect but there is only one perfect person in the Bible. Also he had less wives than David. @Ken i respect your opinion, I disagree but I don’t have all the answers. There are a lot of scammers. But you have to test your beliefs. Einstein couldn’t except quantum mechanics. He said God does not play dice. He would not except something that he didn’t have proper evidence for. But it isn’t just a matter of intellect. If no one shows you the right evidence you can’t make an informed decision. Exposure to the wrong evidence is going to make you suspicious of evidence that is the legitimate fact. I think it was Michio Kaku who said the question to ask a physicist is, “Could God have designed the World any other way.”
-
Sorry I didn’t address you. I think your interpretation of the chaplains letter is fair. But remember some still take the letter to the chaplain as a personal God. I know you said I was projecting Christianity onto Einstein, but much of it was to provide an example. I wanted to see if someone else saw an correlations with belief in a personal God. As I said Einstein is a just man and many of his essay concur with Christian values. To me it would be cool if he was a believer, but I understand if he was not. Heck, with his life he could be considered a saint or prophet 😆 That is why Time made him an of the century. I called his life blessed but we will call it purpose driven well lived life. As far his writings go he never claimed to be a Christian. But his actions such as the scientific discoveries, running from prosecution, warning about nuclear bombs…he is similar to characters from the Bible. Yes much of my examples were based on the man Einstein was and not him stating what he believed. I have read bio’s where the state he was a believer in God. God does not play dice. Why would he say that if his God wasn’t personal. By that I mean the God of Spinoza worries about the position of subatomic particles but not people. I would like to read an article by Einstein calling his God Spinoza. I know Einstein was influenced by Spinoza, and Joigus posted a definite quote against a personal God. I don’t know the context. I guess if Einstein said it it was what he believed. But I still find fault in the god of Spinoza. For what purpose is Einstein working on solving the mysteries of the universe if he doesn’t have a significant purpose in that universe? I mean the God of Spinoza created us then has no interest in his creation. Einstein created relativity. He would defend his work because he is its creator. I don’t think a personal God makes the universe less interesting. Einstein used the word God in his essays. That is going to cause debate. IMHO Einstein failed to address this issue because he didn’t want to effect his work. He was too busy working on a theory of everything. No matter your view on the subject someone will always find fault. And everyone loves and respects Einstein. He knows the importance of his positions. By that I mean he may not believe in a personal God, but he respects the beliefs of those who do.When he says a personal God is something he cannot take seriously, could it mean he concerns himself with the creation of God (Spinoza) and does not wish to invoke himself in human religious practices or rituals? Like the John Lennon song, “Imagine no religion.” After all the religious prosecution of WWIi it is reasonable not to be religious. It would not mean he didn’t believe but maybe find relief in trying to discover the beauty behind how the universe works. In his situation I would not want to deal with anthropological dealings of man. You guys no more about Einstein than me. And nowhere does it say Einstein prayed. Eise your interpretation of the chaplain letter is good. You reflect that Einstein was being spiritual. Christianity is a religion is a religion, but Christians are called to be spiritual and not religious. Einstein could have told the chaplain your son is in heaven just as if the Chaplain would hear from a religious figure. But Einstein is not a religious authority. Instead he decided to share something personal on what he believed. It may or not point to a personal God but what he is saying is our lives matter. There is more to what we are concerned about in our lives. Personal God maybe; probably not. Einstein probably wouldn’t tell us anyway. But looking at his life, actions, and writings any thing is possible.
-
I concede that it is not provable that Einstein was a Christian. But there is indication that he believes in a personal God. And that belief in a personal God is applicable to many religions. That is Jewish or Christian or other faiths I don’t know about. And it isn’t just me who states he believed in a personal God. He mentioned God a lot and it is debatable that he was talking about the God of Spinoza or a God of creation. But it doesn’t mean there are not Christian themes in his writings. He has articles that talk about building a nation for the Jewish people. You are right Einstein was too smart for that. He isn’t going to trash a good idea if it came from a Christian, Jew, or atheist. And you are right Christianity is a religion. But Christians are supposed to be spiritual. Einstein was a just man. He is going to agree with Christians on many topics. He may not mention Jesus but they share many traits. What bothered me about this thread is that no one thought Einstein lived a blessed life.
-
A human being is part of a whole, called by us “Universe”, a part limited in time and space. He experiences himself, his thoughts and feelings as something separate from the rest — a kind of optical delusion of his consciousness. The striving to free oneself from this delusion is the one issue of true religion. Not to nourish it but to try to overcome it is the way to reach the attainable measure of peace of mind This letter is were many claim Einstein was being religious. https://www.facebook.com/rabbinlevy/posts/einstein-wrote-this-poignant-letter-to-a-grieving-father-named-rabbi-robert-marc/398447822088085/ To tell the truth I don’t know Einstein’s intention. He could have said yes your son matters. Telling him we just exist and sometimes bad things happen we must accept it; is not thoughtful and not Einstein’s style. Instead I think Einstein wrote what he believed. It is profound and takes many meanings. But IMHO Einstein is walking a fine line and saying there is a meaningful purpose to what happens in human lives without stating what he believes in such things. But history is not perfect. Nurses don’t speak German. Somebody erases a chalkboard. But next time you read an Einstein essay see if it implies something spiritual.
-
You misunderstand my words. I am saying that there is a possibility that Einstein could have believed in a personal God. It is debatable. The fact is we do not know. So the only way to understand Einstein is what he wrote. I chose to have him saved by the chaplain because religion becomes important at the end of life. I know there are many religions. And I know that everyone does not agree on that subject. But when I read Einstein his writings are not only science but spiritual. Many people use to write Einstein. This included a Jewish Army chaplain who lost his son. This same chaplain had just been deployed to the concentration camps and saw many horrors. Einstein’s reply is left to interpretation. It has been several years since I have read Einstein’s reply but it is worth discussing. But like any letter is open to interpretation. I also believe that Einstein had more to do with the manhattan project. I sill haven’t seen Oppenheimer. But to put the discussion this way: any scientist who had anything to do with that project will seek out a chaplain at some point in their lifetime.
-
I mean at age 80 and a bad heart that Einstein might have been considering a personal God. I think under the same conditions an atheist would consider the same. That is where chaplains come in. What makes the cosmos so inspiring? Understanding it is one thing, but I think what makes it so inspiring is the deeper meaning. Escaping death from Nazis Germany. Making ground breaking discoveries and enjoying life seems like a blessed life. But back to Einstein as a Christian could living in the U.S. introduce him to Christian values. He wrote many essays that were more than just philosophies where he looked to improve society and his adopted American life. So the ingredients are there. I’m saying old Einstein is a different man than young Einstein. He lived through WWII. He also wrote a lot about the Jewish people. Maybe he writing the stuff and doesn’t know it shares many Christian values. And maybe while he is in the hospital a chaplain gets him saved. Easier to understand than relativity.
- 35 replies
-
-2
-
I am not concerned whether a smart man can believe. Of course they can. But there are accounts of Einstein believing in God. There is debate on what sort of God. As exchemist said probably not a personal God. But I have read both views. I was wondering your take. Einstein was not only a great scientist but an awesome person. I was just thinking that his heart was bad and he’s aging does he consider a personal God? A chaplain at the hospital maybe? He was discovering the world’s mysteries. Can these mysteries mean the physical world can be manipulated? And the Holocaust and bomb bring reflection. If Einstein didn’t believe in a personal God why didn’t he know his life was a miracle: he was a Jew that survived his own country trying to kill him. Smart doesn’t mean anything. But he was reflective in his writings. He had to feel his life was blessed.
-
Was Einstein a Christian? I don’t mean if he claimed to be one. But did his discoveries and how those discoveries manipulate the physical world lead him to believe what other ways the physical world could be made?
-
It is a scientific fact that dogs know calculus. They perform it every day finding the shortest path to retrieve the ball that was thrown. So when Newton claimed to “discover” calculus there was much controversy. Not because Leibniz also claimed to “discover” calculus independently. The dogs were much aware of calculus since dogs have lived. Newton observed the dachshunds that he hunted with. Newton ask the wiener dogs how they knew which hole the badgers would go down. That is: the shortest distance to the hole which would often determine the badger’s direction. These interactions influenced Newton just as much if not more than when the apple hit his head. So the arguments between Newton and Leibniz was trival. It should be stated that calculus originated with the wiener dogs.
-

-

Jay Leno was talking about when Columbus discovered America he took back some native Americans with him. But as they stepped on land the native Americans did say, “We have discovered Europe.”
If you are familiar with Hitchhiker’s Guide to the Galaxy you know the mice were smarter than humans.
Also the dog is in control of his position. The rock is not.😝
-
-
Exchemist, you make a valid point. But my desire to resurrect the post is only so all my work can be seen in the same area. It is not obscene or religious preaching or things of such nature. I posted the locked post to share a math idea. An important part of those posts was to document my work and share what I was working on. There is the fact that I keep trying to factor semiPrimes. For that I look like a fool posting. But I am posting with a seriousness. I know my idea seems impossible or as some would say “trival” because I am not reducing the number of computations compared to standard brute force. But I have shown examples of factoring numbers that are small enough for their factors to be known. My equations will not improve the time it takes to factor small semiPrimes. But what I am working on is a way to lessen the computation of large semiPrimes. I have tried to factor a 2048 bit semiPrime. The answer is incorrect, but this could be because of computer calculation and not my graph. You can find my work on the Simple yet interesting thread in mathematics (page 8). But my goal is not to post to the locked thread. I only want it to be viewed if someone reads the simple yet interesting thread. The project is not just choosing random numbers. It also has many elements other than the test equation. I have researched computer science, cryptography, number theory, and more. I want to use the past thread in an academic project. I also feel that if someone does decide to read Simple yet interesting they may find value in the preceding thread. And maybe some of the information in the original locked thread may prove to have more value than before it was locked.
-
I have a request of the Admin. I have a post that is locked. Probably because no one understood what I was trying to do. That is bad communication on my part. The post is: Prime Products just one last tine by Trurl, June 18, 2016 in Mathematics It was locked 5 years ago. This post preceded the post Simple yet interesting. I know it has many mistakes and many failed attempts, but it remains the supporting work of my entire efforts. I know no one believes that I solved the Prime factorization problem, but I request this thread to be unlocked not because I wish to add to it. Instead I want to bump it up to be near to the Simple yet interesting post. Why? I need those that see Simple yet interesting to see the earlier work if they care to investigate the math problem further. The truth is it may show more work no one believes, but I intend to use these works on Prime factorization to an academic project. Right or wrong I want to defend my work. I have never defended an academic work. But I have heard even if the work doesn’t prove the hypothesis, the student can explain the thought process behind the math work. But I still believe in this work. I know the Prime factorization problem is supposed to impossible. But we choose to factor semiPrimes not because it is impossible. We choose to factor semiPrimes because it is not supposed to be possible. I do not wish to make anymore posts to Prime Products just one last time. I just want those who view Simple yet interesting who want to research further see the previous work.
-
Well the shooter was misguided in thinking assignating Trump would change the Republican Party from winning. IMHO. You have to win the Country by becoming a good leader. Taking Trump out of the picture might not even benefit the Democrats. They can’t even decide on the candidate. I saw a YouTube vid of Micho Kaku were he stated he was drafted into the U.S. Army during the Vietnam war and saw a weapons demonstration. He saw the we can blast an enemy and have much more firepower, but this just makes the enemy double down. It is possible to assasinate well known figures, but I don’t think the end result is what the assassin intends. Besides attempting such a thing forfeits the shooter’s life. Trump takes a lot of criticism for stupid things he says, but when he was President there was less wars. He threatened to make NATO pay, but he wouldn’t dismantle it. I find a conundrum with NATO. We join together so that one is attacked we all defend. But instead of securing us we alienate other countries that aren’t members. Does that make other Countries feel they have less influence on what happens in the World? I know that is off topic but I think that should be the issue of the campaign. And assignations will not solve anything.
-

Need description of Prime# distribution in Riemann hypothesis
Trurl replied to Trurl's topic in Mathematics
On a side note, the instructor in the previous post of Prime distribution made a work of fiction in the form of a short film. Warning this is probably appreciated by nerds. But not telling what it is I thought it was a work of art; something that shows the impact of math. https://www.edwardfrenkel.com/film/ -

Need description of Prime# distribution in Riemann hypothesis
Trurl replied to Trurl's topic in Mathematics
https://youtu.be/d6c6uIyieoo It has been awhile since I ask, but I was wondering how proving that proving that zeroes always do or do not exist on 1/2 would be critical to solving the distribution of Prime numbers. I have to watch this video again to find the time he says this. 15:17 minutes in video Is there a difference in “the distribution of Primes” and “the location of Primes?” By location I mean the value or actual determining if a number is Prime. -
Klapacusis you are right it is trivial. This is a game of trivial pursuit. I don’t know the factoring pair of this 2048 bit semiPrime. But if the number of the equation where it equals zero is correct than the factor is less than that number. And I added the percentage of error which brings us closer to that smaller factor. I know your argument is that it is still a large number. However checking all odd numbers descending from my estimate should be close enough to not require as much computation. 4*10^37 divided by 2. Still a bunch of numbers but more manageable. Still too many numbers but the actual factor should be close (slightly less) than the estimate. And if anyone could add any advice in crunching numbers, particularly in Mathematica I would appreciate the help. There is a function call Monitor. I don’t know how to “keep track” of what is happening behind the scenes when Mathematica is processing. It just says, “Running.” I don’t know if it is going to take hours, days, or months. I understand why someone would not believe my methods. We are not supposed to be able to factor semiPrimes. It is impossible. But is it possible for impossible to exists? I chose the largest RSA number that is open source. I don’t know the factors, but I feel I am getting close. RSA is critical for authentication using digital signatures. It is still one of the most used cryptography schemes on the web. I have recently read that the original Xbox used RSA to secure its hardware. I didn’t know cryptography was used in hardware. But don’t be afraid to factor semiPrimes because it will mean the end of RSA. I think it was flawed from the beginning. Secrets can not be keep if you share them. By encrypting secrets you have just marked them as valuable. That is why misinformation is so prevalent in media. 1977 it made sense to encrypt you secrets. Now it is difficult to determine truth from reports. For instance Trump is found guilty on trial. He says witch-hunt ; they say guilty of influencing the election. We hear the verdict, but we weren’t at the trial. We didn’t see all the evidence. And if the County is 50 50 Trump / Biden why wasn’t this reflected in the jury? Politics aside who is right? It all is based on which candidate you believe. But who is trustworthy? I think the true is the same with cryptography. We trust is because we can mathematically test it. If the numbers require too many brute force attempts it is secure. But which crypto systems are trustworthy. If I do go on to break RSA, I hope to break it along with you. If it works, I showed you how to do it. And that you can believe the answer. If I fail and it still is impossible, we have more trust in RSA.
-
Well it worked here: Clear[x,pnp];pnp=2564855351; eqn=((pnp-(Sqrt[(x^2*pnp^4+2*pnp*x^5)+x^8])/pnp^4-(1-(x^2/(2*pnp)))*(pnp^2/x^2))); Solve[eqn==0&&x>=0,x,Reals]//N (*{{x41350.98025},{x6.387801493*10^11}}*) In[1]:= 41350 is close to 41227 By trivial you mean the division. I did not divide yet. I only used the equations. The magnitude should be close. I still have programming limitations on my own part. But I thought the number seemed reasonable. Close enough for good old brute force. What numbers do you get?
-
This is the smaller factor of: RSA-2048 = 2519590847565789349402718324004839857142928212620403202777713783604366202070 7595556264018525880784406918290641249515082189298559149176184502808489120072 8449926873928072877767359714183472702618963750149718246911650776133798590957 0009733045974880842840179742910064245869181719511874612151517265463228221686 9987549182422433637259085141865462043576798423387184774447920739934236584823 8242811981638150106748104516603773060562016196762561338441436038339044149526 3443219011465754445417842402092461651572335077870774981712577246796292638635 6373289912154831438167899885040445364023527381951378636564391212010397122822 120720357 Verify
-
I don’t see the point in Russia trying to influence elections. They’d probably want to but so does either side democrat or republican. The idea of collecting data is to know your target audience. Everyone wants an influential voice so the data is valuable. It would take some resources to power such a weapon. And the corrupt message could be drowned out in a sea of messages. No matter what your opinion someone disagrees. I often wonder if the Trump Biden thing is just to piss everybody off. Instead of having announcements that say go vote, they piss off everyone and it is a record turnout. So the morale is that if you don’t know the motivation behind the influence or control you can’t defend against it. Some things like money earned by selling data is common sense, but imho it would take some “power” to manipulate data on that scale. It would be like a president trying to control the entire government let alone the world. I was brainstorming ideas one night and thought what if we had a computer program that spread misinformation. Say it took your online profile and put in different addresses, phone numbers, and metadata. There probably is already software that does this, but I didn’t want to add to garbage already found on the internet, just the online footprint. I understand why China would want to influence us. And I think go ahead, we might learn something. I don’t know crap about China except they are communist and they take American jobs. Is this true. We know better than that. When I was in high school they said Japanese students are better in math and buy American. Our students are just as bright. Besides Japan are our allies. So I guess blaming China or math scores on Japan makes us study harder. But there are misconceptions all over the world. I guess it makes you loyal to your country and respect your leaders. Misdirection.