-
Posts
926 -
Joined
-
Last visited
Content Type
Profiles
Forums
Events
Posts posted by Function
-
-
is this the sort of thing you are after?
Works perfectly! Thanks, John!
0 -
Hi everyone
I need to imply 2 "IF"-functions in one cell... Is this possible?
Consider 3 cells: A1, B1 and C1.
C1 should display "Yes" if A1 is larger than, or equal to one half of B1 AND it should display nothing if A1 is empty, but not zero (should A1 be zero, then C1 should be "No")!
Is this possible?
I tried on C1:
=IF(A1 >= (1/2)*B1);Yes;No) AND IF(A1 = "";"";"")
But this gives an error.
Can someone give me a line?
Thanks.
F.
0 -
Apologies for the sloppiness, all I had to write on was my desk!
So, if you can read my drawing well enough, you should be able to see that we have:
[math]tan \alpha = \frac{PQ}{OQ}[/math]
[math]tan \beta = \frac{PQ}{QC}[/math]
[math]tan \gamma = \frac{PQ}{QI}[/math]
If we expand out tanx we have:
[math]tan x=\frac{sinx}{cosx} = \frac{x-\frac{x^3}{3!}+\frac{x^5}{5!}-...}{1-\frac{x^2}{2}+\frac{x^4}{4!}-...}[/math]
Now if we let x be very small, then all powers of x will be even smaller. So if we discard all higher order terms, we can approximate tanx with:
[math]tan x \approx \frac{x}{1}=x[/math]
So when the angles in the picture are small, we have:
[math]\alpha \approx \frac{PQ}{OQ}[/math]
[math]\beta \approx \frac{PQ}{QC}[/math]
[math]\gamma \approx \frac{PQ}{QI}[/math]
Oh dear Lord... Thank you for your help and, obviously, your interest in this question! And, please, don't apologize... I didn't expect someone to draw this - let alone on his desk
 I must confess, though, that I'm glad my 'explanation' of the situation was clear enough for you to succeed in drawing almost the exact same picture as is drawn in my syllabus (forgive for not having it scanned - couldn't scan atm)
I must confess, though, that I'm glad my 'explanation' of the situation was clear enough for you to succeed in drawing almost the exact same picture as is drawn in my syllabus (forgive for not having it scanned - couldn't scan atm)elfmotat is pampering you - I was going to ask for a diagram.

This statement probably needs further explanation.
We are approximating arc PQ to the perpendicular from P tp OC. The smaller alpha is the more nearly exact this is.
Which brings me to the sort of conditions we are talking about.
We assume all rays meet the curved surface near the axis OC.
That is alpha small.
Such rays are called paraxial rays.
These conditions are typical of eyes.
We are also approximating the curved surface by a circle.
This is true in spherical lenses and paraxial rays, but not true in tall thin lenses.
CP is a normal because it represents the radius of curvature at P and is therefore perpendicular to the tangent at P.
Thank you, too
 Figured too that we had to take PQ perpendicular to OC.
Figured too that we had to take PQ perpendicular to OC.And yes, the eyes were indeed the subject.
0 -
Hello everyone
Consider a convex surface, a light ray being emitted from point O, being refracted by the surface in point P.
The light ray forms an angle alpha with the line OC, C being the centrum of the convex object. PC forms an angle beta with OC and is the normal in P, the point in which the light ray is being refracted, Q is the intersection of OC and the convex surface, OP forms an angle theta 1 with the normal, the refracted light ray forms an angle theta 2 with the normal, intersecting OC in I, the point in which the image will be projected. Gamma is the angle formed by PI and OC.
My syllabus states:
If alpha is small enough, beta, gamma, theta 1 and theta 2 will also be small and thus:
sin(theta 1) ~ theta 1 and sin(theta 2) ~ theta 2
After some operations, it states:
Expressed in radials, alpha, beta and gamma are approximately:
alpha ~ QP/OQ
beta ~ QP/OC
gamma ~ QP/QI
Can someone explain to me why this is the case?
Thanks
Function
0 -
Update: a light form of epilepsy might be present. Additional possibly related symptom: tremor in lower right eyelid, (quite often, might also be a result of fatigue) occasionally left eyelid.
0 -
Regardless of the fact it doesn't 'seem severe' to you, and isn't affecting your lifestyle I would still check it out with a doctor. Do you have free health consultancy in Belgium?
Nearly free, yes.
How long do they last usually? Do they feel to be predominantly on a particular side of your body or both at the same time?
How long the shocks last? Or the 'waves'? The shocks themselves are as quick as blinking eyes, the waves about 30 secs, with breaks; both sides of the body at the same time
0 -
Is it there consistently or does it appear and disappear?
It's very occasionally, in those situations explicitely described above... Very strange indeed...
Now here's how I'd like to describe it too: it happens in those situations when doing something you're deemed not to, knowing that someone might show up... (E.g. I had to put a letter on a desk in an empty classroom in primary school when I was very young, walking very slowly in the empty classroom (lights turned off), knowing that a teacher might just show up behind me... Okay, I wasn't doing something I was deemed not to, but... Ah screw this I can't explain it any better, sorry!)
0 -
This site can't- and doesn't- supply medical advice.
Go and see a doctor.
I know, but it doesn't affect my lifestyle in any way, nor does it seem severe to me. I don't need medical advice, just a healthy debate on what it might just be

I get what is like a bullet going through my head and I looked it up the next day and I found a syndrome called "exploding head syndrome" I am always nearly asleep, and there is some undefined sensation prior to it, but no sounds as in your case, then this single event, the suddenness of the explosion is like a single "bang". It wakes you up obviously but there are no ill effects after that.
I have had it 3 times in the last year or so.
Exploding head syndrome comes close... But I wasn't asleep.
0 -
When did you first experience your symptoms?<quote> (I quickly get dizzy when standing up).</quote> how long a day do you sit??
Oh boy... Years ago... Like... A lot of years ago... At least 6 years ago, I was in primary school, walking into an empty classroom, slowly, and then they came...
Sit for a quite long time, truth be told... Less in the weekends, however, but I can't put a time on it
0 -
Hi everyone
Few minutes ago, I experienced a 'wave' of shocks in my head. I have experienced these shocks before.
I woke up at 10.45 a.m. Now it's 1.20 a.m.
Normally, I go to sleep at 10.00 p.m. and wake up at 5.00 a.m. (thought it might be important, my hours of sleep)
They start all of a sudden, and last for like, 1 minute or so, with breaks inbetween them (e.g. 5 shocks, brake of 10 seconds, 3 shocks, ...)
I've now been lying on my side, my laptop in front of me (positioned on its side too, just for comfort) and now the shocks began. Can't really explain what they are, but it's like all muscles in my head or whatever (not facial muscles) contract, I hear a high pitch sound for every shock and they follow up quite quickly - reminds me of a quick heart rate. Can't remember if I can 'see' these shocks or if they affect my vision.
The shocks stopped as soon as I turned myself on my back, searching the internet for clues.
I also hear something I regularly hear when I do something else... Something else I can't really explain, but I think it's something with contracting muscles in my ear, or behind my jaw and beyond my ears, can't really explain it, but if I do that, I hear some sort of deep sound, unexplainable. With these shocks, I hear that sound too with every shock.
I said I experienced these shocks before. I usually 'experience' these shocks when I enter a big empty room with no person inside, stepping slowly into that room. I know - it sounds crazy, but don't ask me to explain it more clearly.
One other crazy testimonial: experienced it years ago when I tried to summon spirits with some friends (yes I was very young and no, I didn't believe in spirits and let's switch to another subject before this thread starts to get paranormal).
I think the shocks mostly occur in a state of extreme relaxation.
I don't take any medicine or other drugs. I may have a low blood pressure (I quickly get dizzy when standing up).
I hope anyone can help me on defining what these shocks are.
Thanks.
Function
EDIT: it's like a really hard heart beat... I can also feal it in my hands
0 -
Do you have any experience with vector calculus? I suggest looking into "line integrals." I think I remember Khan Academy having some decent videos on the subject.
So in general you can examine the difference between two points by taking some general path from A to B. The path doesn't have to be a straight line, it could be some curvy path. [math]\hat{r}[/math] is the unit vector in the r-direction. What [math]\hat{r} \cdot d \vec{l}[/math] is telling you is that integral only depends on differences in r. In other words the integral only depends on integrating the r-component of any path from A to B.
If you're familiar with spherical coordinates, For some general curve in spherical coordinate, [math]d \vec{l}[/math] will contain r, theta, and phi components:
[math]d \vec{l} = dr ~ \hat{r} + rd \theta ~ \hat{\theta} + rsin \theta d \phi ~ \hat{\phi}[/math]
from here it's easy to see that [math]\hat{r} \cdot d \vec{l}=dr[/math].
I put it in this notation to make it explicit that V only depends on r. They mean the same thing.
(I do understand some vector calculus (the algebraic operations))
I kind of understand it now. Thank you!
So what about the V(rb), same as Vb?
0 -
[math]\hat{r} \cdot d\vec{l} = dr[/math]. Therefore:
[math]V(r_B)-V(r_A)=-kq \int_A^B \frac{dr}{r^2}[/math]
I understand everything until here:
why is that (the r unit vector times dl equals dr)? I've never really understood the differential concepts too good

And what's [math]V(r_B)[/math]? Is it different from [math]V_B[/math]?
I am trying not to cross post with elfmotat, who I think is doing a grand job, but I would just like to reinforce one comment.
You need to distinguish between potential and potential difference.
This is a common confusion.
Elfmotat is indeed doing a great job.
On the difference between the two: I am convinced of it that I know the difference
 thanks0
thanks0 -
Hmm okay... May have written a mistake (the professor had written that on the blackboard and might've written a mistake while copying...)
The context:
[math]V_B-V_A=-\int_{A}^{B}{\vec{E}\cdot\vec{dl}}[/math]
That's what's explicitely written in the 'book' itself and I accept this - it's negative because of the opposite directions.
Now what I've written on a blank page next to it:
[math]V_B-V_A=-\int_{A}^{B}{E\cdot dl}\cdot\cos{180^{\circ}}[/math]
[math]=\int_{A}^{B}{E\cdot dl}=-\int_{A}^{B}{\frac{q}{4r^2\pi\varepsilon_0}\cdot dr}[/math]
I am guessing that this is the movement of a charge q along a line L from A to B in an electricfield E.
In that case this would be an energy balance saying that the work done intergral (E.dl) equals the potential energy gained.
Did you miss out a dot in the first integral?
But "dl" implies that "l" is variable, is "l" the distance from the charge to the positive point A?
But then I wonder what r is, and why my professor switched to r, turning the integral negative... I'm pretty sure he did write both "r" and "l", but don't get the difference...
What do you mean with "miss out a dot"?
Let me quote the text that is written about the electric potential in my book (my apologies for any mistakes) (most important stuff are bold):
The electric potential difference between 2 points B and A, Vb-Va, is the difference in electric potential energy from the positive unit charge between the points B and A; in other words the electric potential difference between two points B and A is the work that an external force must do to bring the positive unit charge from A to B. The unit of potential difference is the Volt. The electric potential in a random point, V, is the electric potential energy, that the positive unit charge has in that specific point. For this definition, a potential on an infinite distance is being considered zero. The electric potential in a random point is thus the work done by an external force to bring a positive unit charge from infinite, to the specific point. All points with the same potential are forming an equipotential surface. Movement from charges between 2 points on an equipotential surface doesn't need any work. Field forces are perpendicular to these surfaces.
0 -
Hello everyone
Another question, based on an equality from my biomedical physics course:
[math]\int_{A}^{B}{\vec{E}\mathop{}\!\mathrm{d}\vec{l}}=-\int_{A}^{B}{k\cdot\frac{q}{\vec{r}^2}\mathop{}\!\mathrm{d}\vec{r}}[/math]
Question is simple: why?
(Note that I may have written some mistakes with vectorial notation in the integrals)
Thanks!
F.
0 -
Thanks. Think I get it now.
0 -
I don't know if it was clear but my post#10 was meant to be an answer to your question about spare p orbitals in post#9
Sort of; just a small yes or no question: as long as no hybridisation has found place, one of the p-orbitals of an atom is useless?
0 -
Yes, I understand hybridisation, thanks
 0
0 -
Very well, question answered clearly. Thank you both for the scientifical enlightment. +1 each.
Additional, secondary question: so as long as hybridization hasn't found place, one of the P-orbitals will stay 'useless'?
0 -
I have given fuzzwood +1 for getting you to this stage.
However you have not quite drawn the two sp hybrid orbitals quite correctly.
For the situation we are talking about there are two number sp hybrid orbital per atom.
The original p orbitals are symmetric about the origin, both lobes are equal.
The sp hybrids are not. They have one large fat lobe sticking out to one side of the origin and one small tail lobe on the other side.
The fat lobes form the bonds.
Of the two in each atom
On fat lobe sticks out to the left and one to the right (along the x axis)
So the two overlapping fat lobes form a single bond along the x axis and the other bonding lobe for each atom sticks out on the other side of each atom (and therefore can easily bond to a hydrogen).
The other two p orbitals per atom overlap sideways on and form 2 weaker pi bonds
But that's what I've drawn: 1 s-orbital per atom and 3 p-orbitals. That was my intention. I could've drawn sp-orbitals, but then my whole question wouldn't be necessary anymore.
Let me reform my question: is a hybridization of s- and p-orbital into spn-orbitals obliged when promoting an s-electron to a p-orbital?
If not, then why can't just the two sole s-orbits form a sigma-bond, and the three p-orbits each a pi-bond, forming a quadruple bond? (Which was my original question)
0 -
That is exactly how I wanted you to grasp my explanation.

Great, but why won't the electrons just migrate to the parts of the p-orbits between the two atoms, forming a pi-bond lying 'on' the sigma-bond?
0 -
It is the nature of these bonds and the angle that they make with each other.
In an sp3 hybridized system you have 4 equal bonds to other atoms, ideally making an angle of cos-1(-1/3) = 109.47°. In an sp2 hybridized system you have 3 equal bonds with other atoms and an additional pi-bond with one of the 3 atoms. Ideally, the bonds now make an angle of 120°. In an sp hybridized system you have 2 equal bonds with other atoms and two additionals pi-bond with one or 2 of the other atoms. Ideally, the bonds now make an angle of 180°. The reason behind these angles is that the elektrons making up the bonds are as far away from the other bonds as possible.
The orbitals making up the pi bonds are perpendicular to the one making the sigma bond. To engage in a pi bond with another atom, these p orbitals sort of have to bend towards each other. This works for the px and py orbitals, but not for the pz orbital as that one is antiparallel to the sigma bond and thus has to wrap around the entire atom for it to reach the other orbital. You can imagine the strain on this bond to exceed whatever bonding force the bond might have.
i'm really convinced that your answer would make sense to me if I could visualize this...
see the image attached here; is the orange line that prevents the C-atom to undergo 3 pi-bonds in casu?
If so, why couldn't the electrons in these 'problematic' p-orbits just move to the part of the p-orbits that lie between the two atoms, between the sigma-bond?
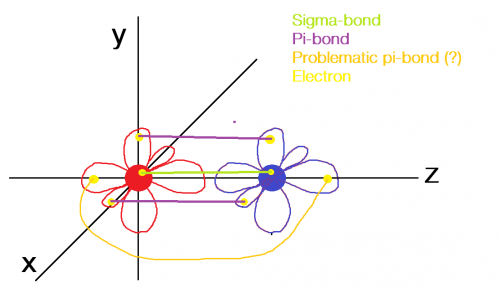 0
0 -
Hi everyone
Just wondering what's the problem with a quadruple bond between two C-atoms.
Why is this not possible?
I mean, if you promote an electron from the full s-orbit to the empty p-orbit, without hybridization, on each atom, why can't they have one sigma-bond and 3 pi-bonds? Or is hybridization 'obliged' with promotion of an s-electron?
Thanks.
F.
0 -
I'm going to change your variable O to an A, because I don't like it (it looks too much like zero). So we have:
[math]U=\int_{0}^{\Delta l} F dl[/math]
[math]\sigma =F/A[/math]
[math]\epsilon =\Delta l/l[/math]
We can first replace F with [math]F= \sigma A[/math]:
[math]U=\int_{0}^{\Delta l} \sigma A dl[/math]
Now we also have [math]\Delta l= l \epsilon [/math]. In the limit that [math]\Delta l[/math] becomes smaller and smaller it becomes [math]dl[/math], and [math]\epsilon[/math] becomes [math]d \epsilon[/math]. So our equation with differentials becomes:
[math]d l= ld \epsilon [/math]
Since we are changing variables we also need to change the limits of integration, which is where the strain in the upper bound comes from. (If change in length goes from 0 to Δl, then strain goes from 0 to ϵ.)
So after all of our substitutions, the integral becomes:
[math]U=\int_{0}^{\epsilon} \sigma A l d\epsilon[/math]
Enlightening. Thanks.
("O" stands short for "oppervlakte", Dutch for "area", yet your irritation is agreeable
 ; I don't agree the choice of your word "variable", however...)0
; I don't agree the choice of your word "variable", however...)0 -
Sorry, but I still can't seem to understand why the second integral is equal to the first one...
0

Excel: 2 IF functions
in Computer Science
Posted · Edited by Function
Please quote my sentence that stated I wanted to do that.
There is none.
Ask before you insinuate.
There's no table I want to copy. It's a table I make myself, in order to have a nice view of my university results in juanuary/february for my former high school teachers