phillip1882

i also wanted to add, if you spin the ship fast enough, you stick to the walls

no, but that's because gravity counter acts the effect. yeah i understand, i was wrong, force doesn't necessarily require energy, but we should clearly indicate when force is being applied

no its velocity, you can experience this with your car, when you turn your thrown to the side some. clearly force is being applied.

so, i used to have a beef with newton. i thought that an orbiting body should require the expenditure of anergy. with the strong nonclear force i can understand not requiring energy, there's no motion and therefore no change in velocity and therefore no acceleration and therefore no force. but with an orbiting body there's change in velocity, a change in direction, therefore force, and force should require the expenditure of energy. but then i envisioned a pole with one end of rope tied to a pole and the other end tied to a rock, if you put the rock "into orbit" around the pole, yes the rope is applying force, but i see no reason discounting friction it can't obit indefinitely. clearly not all force requires energy expenditure.

hmmm. lets say n is 7, 72 × 1 + 36, = 108 72 × 2 + 36 = 180 72 × 3 +36 =252 72 x 4 +36 = 324 72 x 5 +36 = 396 72 x 6 +36 =468 72 x 7 +36 =540 adding all of them together, i get 2268. I'm not sure where the +35 is coming from, but lets add that as well, 2303 from here, how would you determine p and q?

according to euler, the infinite series 1+2+3+4+5.... = -1/12. the "proof" is a bit complex, but basically revovles around letting the series 1-1+1-1+1-1 = 1/2 here's my problem with this. let S = 1 +1/2 +1/3 +1/4 +1/5 +1/6 ... multiply S by 2. 2*S = 2 +1 +2/3 +1/2 ++2/5 +1/3 ... subtract S 2*S -S = 2 + 2/3 +2/5 +2/7 +2/9 ... subtract S again 2*S -S -S = 1 +2/3 -1/2 +2/5 -1/3 +2/7 -1/4 +2/9 -1/5 0 = 1 +1/6 +1/15 +1//28 +1/45... which aproaches a finite value greater than 0.

there are already 5 dan cpus but making a 9 dan one would be quite hard

this is a cool idea i found over at xkcd forums. for a number n, if n is composite, break it into its prime factors. if n is prime, place '<' '>' around the number and determine the n'th prime its is. then the first 20 numbers are... 1 <> 2 <<>> 3 <><> 4 <<<>>> 5 <><<>> 6 <<><>> 7 <><><> 8 <<>><<>> 9 <><<<>>> 10 <<<<>>>> 11 <><><<>> 12 <<><<>>> 13 <><<><>> 14 <<>><<<>>> 15 <><><><> 16 <<<><>>> 17 <><<>><<>> 18 <<><><>> 19 <><><<<>>> 20 a symmetric number is a number that can be written symmetric about the middle. the first few are 1 <> 2 <<>> 3 <><> 4 <<<>>> 5 <<><>> 7 <><><> 8 <<>><<>> 9 <<<<>>>> 11 <><<>><> 12 <><><><> 16 <<<><>>> 17 <<>><><<>> 18 <<><><>> 19 <><<<>>><> 20 <<<>><<>>> 23 <<<>>><<<>>> 25 <<>><<>><<>> 27 <><<><>><> 28 <<<<<>>>>> 31 <><><><><> 32 <><<>><<>><> 36 <<><<>><>> 37 hypothesis: 1) numbers that differ by true value of 1 won't differ by number of backets by more than 2. 2) symmetric numbers follow a logrithmic growth rate similar to the primes. 3) there is no general algorithm for adding recursive numbers.

I ask this in the most serious way possible: what drugs are you taking? nothing that hasnt been perscribed to me. i've taken abilify to combat some earller bipolarism. i'm currently on some medication to fight any voices which i seem to now sometimes hear since atempting suicide. the medications im on are ripisadol a divaporeox. the reson i bielve in the supernatural is it seems to be not just me but things outside myself acting oddly as well. such as people know things about me that i didnt tell anyone, or people acting in a bizzare manner.

so here is a small list of some of the experainces i had. when i went into the hospital, there were two weman there who i had never met who seemed to know exactly why i was there. one seemed to want to help me the other to condem me. after i got out, in the morning i woke up, my whole body seemed full of light. i dont know how else to describe it other than that. lightr radiated through out my skin. i read the bible and it said my word was truth. i condemned the world by saying one lie, one cheat, one steal is worth a pushment of hell. i went online and people were begging to be realased on a chat sever i regularly visit. i freed everyone, by freeing the worst person, krossos, who i later remembered from a book i read a long time ago is the god of death and destruction. he struck deals with people for their release. he had aparently had aleady been freed 7 times. the bible continued to communicate with me. jesus said he was the true god of isreal and that i should know that becuase he sent me two helpers. after a couple months i experanced a sort of 4th dimential reality. seasons shifted rapidlty, flowers grew and wilted in rapid succession, people scrabled for basic food. shortly after, i had a sensation of my head dissolving in acid, after it was over, i read the bible and the apostle paul said i was sentanced to satan to atone. a tv repairman came to my house to install direct tv. after he was done, i said, i leave you to your work, then he said in a near panic, "no your good your good." then he ran up stair, ran back down stairs, and stepped on my toe. he said i didnt step on oyur toe did i, and i said no as a way of forgiving him. then he said your running the show now. then the television seemed to be commucating with me in a simalar fashion as the bible. i read the bible and it said that i was satan, but that satan cant spit in his own eye. so i spit in my own eye to end it. there's more to it, but just to give you a general idea.

so, let's start from the beginning. the harmonic series: 1/1 +1/2 +1/3 +1/4 ... grows indefinitely. however the series 1/1 +1/2^2 +1/3^2 +1/4^2 etc. aproaches a value, specifically pi/6 (or was it pi^2/6? well the point is its finite) in general 1/2^s +1/3^s +1/4^s ... aproaches an interesting value (something in terms of pi.) whenever s is even. now if we modify the equation in a few ways: first well do 1- each term. 1- 1/2^s +1-1/3^s +1-1/4^s... then we'll take the reciprical of each term. 1/(1-1/2^s) +1/(1-1/3^s) +1/(1-1/4^s)... then we'll multiply rather than add. 1/(1-1/2^s)*1/(1-1/3^s)*1/(1-1/4^s)... and finnally we'l exclude any non prime power terms. 1/(1-1/2^s)*1/(1-1/3^s)*1/(1-1/5^s)*1/(1-1/7^s)... it turns out this is exaclty equvalent to our original equation 1/1 +1/2^s +1/3^s... (its possible to prove this but admittedly i don't know how, im not expert. although this looks ugly, this multiplication means that if we can get the right side to be non-trivally zero we have information we can use to estimate the gap between primes. all trival zero occur whenever s is even. all non-trivail zeros occur when s = a +1/2*sqrt(-1) where a is some unkown value. or at least this is the hypothesis, its never been proven.

so, on my 31'st birthday i tried to commit suicide. i survived, but after which over the course of the next 3 months i had a bizzare set of experances, that let me to believe that there is a supernatural element to the universe. i can't prove this of couse, all i have is alot of allegation about my experiances, but it is enough to make me believe. i chose christainty admitedy becuase it's what i grew up with. had i beem born in the middle east i'd probalby would consider myself muslim. but regardless, i truly believe that there is an element beyond what science can explain.

if you need any help i am available to go over most of the basics. email me at phillip1882@yahoo.com

if the number of paths at each split is fixed, then the general equation is... r^(n+1) -r ------------- +1 r -1 if not then I'm afraid you'll just have to add. lets say number of paths at each split is 5 and you have 4 levels. 5^(4+1)-5 -------------- + 1 = 781 5-1

it doesn't matter, so long as all cases are covered.

i'm afraid your question is too poorly worded to really give an adequate answer. the best i can do is try to explain what i THINK you're saying and then answer that question. what you have is a pathing question, and you want to know how many different paths you can take. lets take a few examples and see if we can come up with a general formula. its always good to start with the dead obvious cases, to make things clear. A 1 path A B 2 paths (A, B) A->(1) B 3 paths (A, A:1, B) A->(1,2) B->(1,2,3) 7 paths (A, A:1, A:2, B, B:1, B:2, B:3) A->(1,2) A:1->(1,2,3) A:2->(1,2) B->(1,2,3,4) B:2->(1,2) B:3->(1,2,3) 18 paths (A, A:1, A:2, A:1:1, A:1:2, A:1:3, A:2:1, A:2:2, B, B:1, B:2, B:2:1, B:2:2, B:3, B:3:1, B:3:2, B:3:3, B:4) is this correct?

umm, that doesn't quite make sense. if row m column n = n*m then row 3 column 4 = 12 and row 2 column 6 = 12 and row 1 column 12 = 12 do you see the problem? i believe the standard algorithm is something like the following: linear value = row*total columns +column.

while somewhat interesting in the sense that 2 is the only number with this property, (2+2 = 4; 2*2 = 4; 2^2 = 4) it's not much challenge to define a growth operator where this is not true. for example, let's say # is 2*a +b -1. any number can be reached with smaller values, assuming 1 is given. 1 # 1 = 2 1 # 2 = 3 2 # 1 = 4 2 # 2 = 5 and so on. if you desire the commutative property this is only slightly more challenging. let # = (a << 1) x b |(b << 1) x a -1 where << is left shift, x is xor, and | is or. 1 # 1 = 2 1 # 2 = 4 1 # 3 = 6 2 # 2 = 5

one of my personal favorites is the subtract multiply method. 89 * 97 ------- 100 subtract from each. 100 -89 = 11 *100 -97 = 3 ------- subtract one the two numbers with the cross wise multiplication value. (ie. either 97 - 11 or 89 - 3) 89 11 * 97 3 ------- 86 multiply by the amount subtracted. 89 11 * 97 3 ------- 8600 multiply the two subtracted values, and add. 89 11 * 97 3 ------- 8600 + 33 -------- 8633 unfortunately this is sort of a special case multiplication, and can only be effectively done when the two numbers are fairly close together,

okay, i think i understand what you are saying. let's say there are 200 boxes; our population. each box has several features: size, material, wieght, shape, packing, and wrapping. each feature can have one of several values. to accurately represent a box, requires a random string of data; lets say 30 bits long. with 200 boxes, that's 200*30 bits; plus an error correction, requireing 200*1.3327 more bits. however, becuase we dont care about the order of the boxes; only thier identification, we can reduce this by 200*lg2 200; and likely are able to reduce it further for any rare or unused features. makes sense.

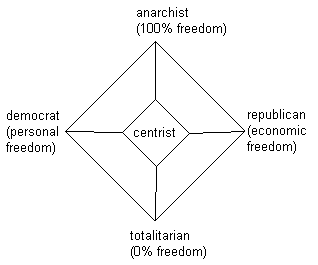
"the important thing is not left or right, there is no left or right, only up or down. up, toward the wings of freedom, or down, toward the ant hill of totalitarianism." - ronald reagan i tend to agree. here's what has been viewed as the political spectrum. i personally consider myself fairly close to the anarchist position. i often find myself critisizing government action. here's 20 questions to help you deside where you are; for each question, answer 2) strongly agree 1) slightly agree 0) niether -1) slightly disagree -2) strongly disagree and give you self the point value accordingly. #1 private business has the right to discriminate against workers for any reason. #2 all drugs should be leagal. #3 government has no right to regulate marriage. #4 government has no right to censor speech. #5 taxation is theft. #6 owership of guns should not be regulated by government. #7 education should be privatized. #8 taxes should not be spent to help the poor. #9 money should be attached to a commodity, such as gold or silver. #10 inflation is a form of tax. #11 interest rates should be determined by private banks, not the government. #12 fractional reserve banking is a leagal practice, if the consumer agrees. #13 the government should not handle retirement plans. (social security should be abolished.) #14 if the free market cannot solve a problem, niether can the government. #15 if accused of a crime, you should have the right to a trial by jury, no matter the crime. #16 military should be handled by a central athority. #17 roads should be handled by government. #18 the government has the right to use force for things other than self defence. #19 the government has every right to borrow money. #20 government should try to regulate the economy. for questions 1-5, move youself to the left if you strongly or slightly agree, to the right if you strongly or slightly disagree. for questions 6-10, move yourself to the right if you strongly or slightly agree. to the left if you strongly or slightly disagree. for questions 11-15, move yourself up if you strongly or slightly agree. down if you strongly or slightly disagree. for questions 16-20, move yourself down if you strongly or slghtly agree, up if you strongly or slightly disagree.

i guess i don't quite understand the problem. let's say we have 7 individual objects, boxes. each box has a distinguishing feature, a binary serial number. how long would the serial number need to be in order to determine which box is which? seems to me you would only need 3 bits. with 128 boxes, you would need 7 bits. in general, the number of bits necessary is proportional to the number of individuals; lg2 n. with over 7 billion people on the planet, is seems to me one's individuality costs 33 bits roughly.

so lately I've been studying randomness for no particular reason. the problem with most prng is they use both multiplication and modulus, both expensive, and are not necessarily very good at producing randomness. i believe i've come up with a nice, compact pseudo-random number generator. here it is in python. v = [0]*3 seed1 = 1995714531 v[0] = 0x96696996 v[1] = seed1 v[2] = 0xb5b5adad def rot(x,k): return ((x<<k)|(x>>(32-k)))&4294967295 #the &num is unnecessary in other programing languages def rng(): v[0], v[2], v[1] = rot(v[2],8), rot(v[1],17), v[0]^(~v[1]&v[2]) return v[1]

okay that makes much more sense. so basically what you're looking for is the number of times a "horse" gets ranked 1-3, with the best horses given the highest chances of winning. for example, horse 3 in the data block at the initial post should receive a high probability, as should horse 5. in particular, the first non-identity column gives the best chances for winning, so 2 should also receive a high probability. with the reference to learning algorithms, I'm guessing you want the computer to figure out how valuable each column is, based on the number of wins and losses each horse receives with the given data. give me a few days, let me see what i can drum up.