-
Posts
719 -
Joined
-
Last visited
-
Days Won
2
Content Type
Profiles
Forums
Events
Posts posted by Daedalus
-
-
Couldn't we explain the "perceived" acceleration of the expansion of the universe as the speed of light decreasing over time as you have suggested in your book? In other words... if the speed of light was getting slower, then we would see this as an acceleration of the expansion of space. Also, couldn't this concept be applied to both Pantheory and to the Big Bang theory? If applied to the Big Bang, wouldn't that mean that light had a higher speed limit which could possible describe inflation? I'm not really sure either way. I just thought I would throw that out there. I also have enjoyed reading you book. I find your explanations for observed phenomena very interesting : )
0 -
All current scientific data shows (a) no real effect of EM waves on the brain (unless from VERY VERY close, and even then rather small one) and (b) no evidence for ghosts or anything "paranormal
I agree. I'm not convinced that EM radiation is the cause. That notion does not make much sense considering that we are emersed in EM radiation throughout most of our lives. However, sound has been known to cause several ghostly effects due to resonant frequencies. However, this does not directly affect the brain, but produces phenomena that seems to be supernatural : )
Research by Vic Tandy, a lecturer at Coventry University, suggested that an infrasonic signal of 19 Hz might be responsible for some ghost sightings. Tandy was working late one night alone in a supposedly haunted laboratory at Warwick, when he felt very anxious and could detect a grey blob out of the corner of his eye. When Tandy turned to face the grey blob, there was nothing.The following day, Tandy was working on his fencing foil, with the handle held in a vise. Although there was nothing touching it, the blade started to vibrate wildly. Further investigation led Tandy to discover that the extractor fan in the lab was emitting a frequency of 18.98 Hz, very close to the resonant frequency of the eye given as 18 Hz by NASA.[20] This was why Tandy had seen a ghostly figure—it was an optical illusion caused by his eyeballs resonating. The room was exactly half a wavelength in length, and the desk was in the centre, thus causing a standing wave which caused the vibration of the foil.[21]
Tandy investigated this phenomenon further and wrote a paper entitled The Ghost in the Machine.[22] Tandy carried out a number of investigations at various sites believed to be haunted, including the basement of the Tourist Information Bureau next to Coventry Cathedral[23][24] and Edinburgh Castle.[25][26]
0 -
Since noone has solved the second part of my challenge, I will post the answer.
Uncool solved the first part using the following "odd / even" equation:
[math]\frac{1-(-1)^x}{2}[/math]
The above equation produces a zero if [math]x[/math] is an even integer, and one if [math]x[/math] is an odd integer. We can arrive at the solution uncool derived by solving the equation which predicts the summation of the above equation:
[math]\sum_{x=0}^n \frac{1-(-1)^x}{2}=\frac{ 2\, n - (-1)^n + 1}{4}[/math]
To obtain the equation which gives us the rest of the sequences we must first derive an equation which produces the Sierpinski triangle. This can be done if we apply the odd / even function to continued summations of [math]x[/math]. Basically, we sum the sequence produced by [math]f(x)=x[/math]. Then, we continue to sum the new sequence to produce the next sequence:
[math]F(S, n)=\sum_{j_{1}=1}^n \sum_{j_{2}=1}^{j_{1}} ... \sum_{x=1}^{j_{S}} (x)[/math]
The Sth summation of [math]x[/math] from 1 to [math]n[/math] can be generalized as follows:
[math]F(0, n)=\sum_{x=1}^n 1=n[/math]
[math]F(1, n)=\sum_{x=1}^n x=\frac{n\, (n+1)}{2}[/math]
[math]F(2, n)=\sum_{x=1}^n \frac{x\, (x+1)}{2}=\frac{n\, (n+1)\, (n+2)}{6}[/math]
[math]F(S, n)=\prod_{j=0}^S \frac{n+j}{j+1}=\frac{\Gamma(S + n + 1)}{\Gamma(n) \, \Gamma(S + 2)}=\frac{\left \langle n \right \rangle_{S+1}}{(S+1)!}[/math]
[math]\left \langle x \right \rangle_{n}[/math] seen used in the above equation is the rising factorial or Pochhammer symbol. I prefer this notation instead of the other variations so that it is not confused with powers / exponents.
[math]F(S, n)[/math] produces the following sequences:
[math]F(0, \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10\})=\{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}[/math]
[math]F(1, \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10\})=\{0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55\}[/math]
[math]F(2, \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10\})=\{0, 1, 4, 10, 20, 35, 56, 84, 120, 165, 220\}[/math]
Plugging this result into the "odd / even" function produces a series of ones and zeroes which gives us the Sierpinski triangle:
[math]\frac{1-(-1)^{F(S, n)}}{2}[/math]
which produce the following sequences (we start with [math]S=-1[/math] and [math]n=1[/math] so that we can see the triangle):
[math]F(-1, \{...\})=\{1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,...\}[/math]
[math]F(\ \ \, 0, \{...\})=\{1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,...\}[/math]
[math]F(\ \ \, 1, \{...\})=\{1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,...\}[/math]
[math]F(\ \ \, 2, \{...\})=\{1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,...\}[/math]
[math]F(\ \ \, 3, \{...\})=\{1,1,1,1,0,0,0,0,1,1,1,1,0,0,0,0,1,...\}[/math]
[math]F(\ \ \, 4, \{...\})=\{1,0,1,0,0,0,0,0,1,0,1,0,0,0,0,0,1,...\}[/math]
[math]F(\ \ \, 5, \{...\})=\{1,1,0,0,0,0,0,0,1,1,0,0,0,0,0,0,1,...\}[/math]
[math]F(\ \ \, 6, \{...\})=\{1,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,1,...\}[/math]
Now if you want the actual triangle pattern you will need to shift [math]n[/math] by [math]-(S+1)[/math]:
[math]\frac{1-(-1)^{F(S, \,n-(S+1))}}{2}[/math]
But, we can see from the above sequences that [math]F(0, n)[/math] produces the double counting sequence from the first part of my challenge. We can also see that [math]F(2, n)[/math] produces the second sequence because it generates a one followed by three zeroes and repeats. [math]F(6, n)[/math] produces the third sequence because it generates a one followed by seven zeroes and repeats. etc...
We can see from the Sierpinski triangle that the sequences we want occurr at the following values of [math]S[/math]:
[math]\{0, 2, 6, 14, 30, 62, ...\}[/math]
The equation which predicts these sequences is [math]2^{m+1}-2[/math] starting with [math]m=0[/math]. Substituting this equation for [math]S[/math] and summing the result gives us the solution for part two:
[math]G(m, n)=\sum_{j=0}^n \frac{1-(-1)^{F(2^{m+1}-2,\,j)}}{2}=\sum_{j=0}^n \frac{1-(-1)^{\frac{\Gamma(2^{m+1}+j-1)}{\Gamma(j)\, \Gamma(2^{m+1})}}}{2}[/math]
Interestingly enough, continued summations of [math]x^p[/math] produce the same result. I solved this equation when I was in the 11th grade in high school. The following is a generalized equation which produces the polynomials that predict the Sth summation of [math]x^p[/math] from 1 to [math]n[/math], where [math]p[/math] is any natural number not including zero:
[math]F(S,\, n,\, p)=\sum_{j_{1}=1}^n \sum_{j_{2}=1}^{j_{1}} ... \sum_{x=1}^{j_{S}} (x^p)=\sum_{j=0}^p \left((-1)^{j+p} \left(\sum_{k=0}^j \frac{k^p \, \left \langle -j \right \rangle_{j-k}}{(j-k)!}\right)\left(\frac{\left \langle n \right \rangle_{j+s}}{(j+s)!} \right)\right)[/math]
Mathematica implements the rising factorial, [math]\left \langle x \right \rangle_{n}[/math] , using:
[math]\text{Pochhammer}[x, n][/math]
0 -
Hi mooeypoo,
I've seen a documentary where they attribute the "sensing / seeing of ghosts" to infrasound. I don't remember which show it was but the following link also discusses the concept:
http://science.howstuffworks.com/science-vs-myth/afterlife/ghost3.htm
Wikipedia also mentions the effect near the bottom:
http://en.wikipedia.org/wiki/Infrasound
I do realize that you posted this topic seven years ago, but it is interesting to see that scientists are still doing research into the paranormal and comming up with sound explanations for what we see and experience.
0 -
I'm not sure exactly what you are getting at, but you can generalize polynomials:
[math]f(x)=\sum_{j=0}^{n-1} a_j \, x^{p_j}[/math]
where [math]a_j[/math] and [math]p_j[/math] are any real numbers and [math]n[/math] is the count of terms, or more accurately defined as:
[math]f(x)=\sum_{j=0}^{n} a_j \, x^{n-j}[/math]
where [math]a_j[/math] are real numbers, [math]n+1[/math] is the count of terms, and [math]n[/math] is the highest power.
You can even have quintic polynomials and beyond:
Unless of course you are referring to a generalized equation for finding the roots of any polynomial.
0 -
ill point out why you are wrong. an impact with the earth will never organize anything into a complex shape or structure or life of any kind. this fundamental flaw in your understanding of physics seems to be extremely prevalent in the scientific community. the notion is ridiculous and unacceptable.
Apearantly, you do not keep up with mainstream science. You haven't even considered ocean impacts which vaporize millions of gallons of water, adding energy to the organic soup which "might" help create organic molecules:
http://www.scientifi...roil-meteorites
The above information is based on the experiments performed by Miller and Urey:
http://en.wikipedia....Urey_experiment
You try to argue that I do not understand physics by making vague statements without showing why I am incorrect. I suggest that you become thoroughly familiar with the subject matter you are refuting, instead of attacking those who make valid points based on scientific evidence.
throw some tobacco on the ground and a rolling paper along side of it and ask yourself how long before a cigarette forms. it will never happen.
Your analogy is horrible. A meteorite impact is not the same as throwing tobacco on the ground alongside a rolling paper in hopes that a cigarette will form. The meteorite impact puts energy into the system. The statement you made does not allow the ingredients of a cigarette to form a cigarette. This clearly indicates that you do not understand the physics involved and lack basic knowledge of biology and organic chemistry.
i can say the life cannot happen as a result of chance... you however cannot say it did. end of discussion. i already proved this point adequately using Newtonian determinism.
Yes, you could say that life cannot happen as a result of chance. But, that does not allow us to conclude that you are correct and it definitely does not end the discussion just because you believe that you have adequately applied Newtonian determinism. My statement in regards to meteorite impacts is more in line with Newtonian determinism than you just stating that you are correct. I have shown that meteorites apply energy into a system, which might generate the means for life to form (i.e. The cause and effect of an ocean impact and the environmental changes following such event which might allow organic molecules to form). However, there is no guarentee that such an impact will form these molecules which leads us to the chance of such things occurring and the probability that life will form due to these, or any other, events.
Also, you did not acknowledge that I gave you partial credit in that life forming was too good for chance alone. The point I made was that it takes both, chance and predefined laws of physics, for life to form. This follows my belief that the universe is so perfectly balanced that it is also unbalanced (chaos and order). If the laws of physics did not allow life to form, then we wouldn't be here today debating your topic. You are arguing that life did not form by chance, when I am stating that it was by chance that life formed on Earth due to the probability that our planet met the criteria.
0 -
-
I've been playing the beta for about a day now and I absolutely love it! The game play is just as you would expect from the Battelfield series. There are a few bugs to work out and some things to adjust. But, this is what one would expect with a beta version of the game.
The rank system seems a lot better because you do move up in rank much quicker than in BF2. The unlocks associated with going up in rank are definitely worth the effort and are vital if you wish to compete.
The only thing I did not like with BF3 is the flashlight. They have extended the flashlight to provide a blinding effect for those looking at it. Even though this does give some realism to the game, the effect is over-exaggerated as even the laser scopes will blind you. The blinding effect is not like a flash grenade, but it does make it hard to pinpoint your target. On the bright side, enemies using their flashlight do expose their position : )
The beta did not include maps with vehicles (tanks, helicopters, jets, etc...). So I am not able to report on any changes made to these systems. But the weapon systems have been improved and shooting the corners of some walls will actually break pieces of the wall out.
I will give the beta version of this game an 8 out of 10. I expect the full version to be even better because they have brought back the jets : )
0 -
Shouldn't this thread be in speculation?
0 -
So are you going to post some math and data to show this "absolute" precision?
0 -
I'm not sure how many gamers we have here at SFN, but Battlefield 3 is open for Beta!!!
I'm downloading it right now. I'll let you all know how awesome it is : )
0 -
It's time to give you all a hint for part 2. The solution can be found in the Sierpinski triangle : )
0 -
I think this thread is insulting to actual wizards. Let me explain... A wizard in the traditional sense, actually studies physical phenomena and learns / shares their information with other wizards. They exploit their knowledge of the universe to create wonderful devices and perform amazing feats, which to the average person seems to be magical.
I think the movie, "The Prestige", puts it best with the magician's explanation of Nichola Tesla in that he is a true wizard. The magician can only trick the audience into believing that they know something about the world, and they hoard their knowledge so that others won't be able to expose them as frauds. But a true wizard needs no illusion, because they know mathematics and the laws of nature which makes them truly powerful and awesome.
A wizard is simply any individual that has failed the to transition from chilhood learning mode into the "pack mind" of a normal human adult.
It is my belief that you are confusing wizards with magicians. Mainly because it is the magicians of the world who have failed the transition from the chilhood learning mode. This is clearly demonstrated in how a magician covets their illusions and tries to trick their audience instead of mastering nature and accomplishing truly amazing tasks.
1 -
Sage is probably one of the most powerful, as it integrates many of the other systems under a common interface.
Awesome post Schrödinger's hat. I'm going to have to check out Sage. It does just about everything Mathematica can do except Diophantine equations. The best part is that it is licensed under GPL.
0 -
Time Dilation - W and X axes
Now we will look at time dilation for the W and X axes. The process is the same as we have worked out previously:
[math]w(u)=\Delta \tau\left (\mathit{Vl}_w \, \left (n+u\right ) + \mathit{Wl}_0\right ) \cos \left (\pm \frac{2\, u-1}{2\, \mathit{Vl}_w \, \left (n+u\right ) + 2\, \mathit{Wl}_0}\right )\cos \left (\frac{\mathit{Vl}_x \, \left (n+u\right )+ \mathit{Xl}_0}{\mathit{Vl}_w \, \left (n+u\right ) + \mathit{Wl}_0}\right)[/math]
[math]x(u)=\Delta \tau\left (\mathit{Vl}_w \, \left (n+u\right ) + \mathit{Wl}_0\right ) \cos \left (\pm \frac{2\, u-1}{2\, \mathit{Vl}_w \, \left (n+u\right ) + 2\, \mathit{Wl}_0}\right )\sin \left (\frac{\mathit{Vl}_x \, \left (n+u\right )+ \mathit{Xl}_0}{\mathit{Vl}_w \, \left (n+u\right ) + \mathit{Wl}_0}\right)[/math]
[math]y(u)=\Delta \tau\left (\mathit{Vl}_w \, \left (n+u\right ) + \mathit{Wl}_0\right ) \sin \left (\pm \frac{2\, u-1}{2\, \mathit{Vl}_w \, \left (n+u\right ) + 2\, \mathit{Wl}_0}\right )[/math]
Now that we have the equation in the form that defines motion with uniform velocity along the W and X axes, we can simplify the terms inside the square root of the arc length integral:
[math]w'(u)^2+x'(u)^2+y'(u)^2=\Delta \tau^2 \left ( \frac{\left(\mathit{Vl}_w \left(2\, n+1\right ) + 2\, \mathit{Wl}_0\right)^2}{\left(2\, \mathit{Vl}_w \left(n+u\right ) + 2\, \mathit{Wl}_0\right)^2}+\frac{\left (\mathit{Vl}_x \, \mathit{Wl}_0 - \mathit{Vl}_w \, \mathit{Xl}_0\right )^2}{\left (2\, \mathit{Vl}_w \left(n+u\right ) + 2\, \mathit{Wl}_0\right )^2}\cos^2 \left(\frac{2\, u-1}{2\, \mathit{Vl}_w \, \left (n+u\right ) + 2\, \mathit{Wl}_0}\right)+\mathit{Vl}_w^2\right )[/math]
Next we will undo the natural units for the speed of light (Note: the equations are getting too big for LaTeX to display the image. We will define smaller equations so that we can put everything together):
[math]\alpha^2=\frac{\left(\frac{\mathit{Vl}_w}{c} \left(2\, n+1\right ) + 2\, \frac{\mathit{Wl}_0}{c}\right)^2}{\left(2\, \frac{\mathit{Vl}_w}{c} \left(n+u\right ) + 2\, \frac{\mathit{Wl}_0}{c}\right)^2}=\frac{\left(\mathit{Vl}_w \left(2\, n+1\right ) + 2\, \mathit{Wl}_0\right)^2}{\left(2\, \mathit{Vl}_w \left(n+u\right ) + 2\, \mathit{Wl}_0\right)^2}[/math]
[math]\beta_{x}^2=\frac{\left (\mathit{Vl}_x \, \mathit{Wl}_0 - \mathit{Vl}_w \, \mathit{Xl}_0\right )^2}{\left (2\, \mathit{Vl}_w \left(n+u\right ) + 2\, \mathit{Wl}_0\right )^2}\cos^2 \left(\frac{2\, u-1}{2\, \mathit{Vl}_w \, \left (n+u\right ) + 2\, \mathit{Wl}_0}\right)=\frac{\left (\mathit{Vl}_x \, \mathit{Wl}_0 - \mathit{Vl}_w \, \mathit{Xl}_0\right )^2}{c^2 \left (2\, \mathit{Vl}_w \left(n+u\right ) + 2\, \mathit{Wl}_0\right )^2}\cos^2 \left(\frac{c \left (2\, u-1\right )}{2\, \mathit{Vl}_w \, \left (n+u\right ) + 2\, \mathit{Wl}_0}\right)[/math]
[math]\beta_{w}^2=\left (\mathit{Vl}_w\right )^2=\left (\frac{\mathit{Vl}_w}{c}\right )^2[/math]
Putting everything together we get:
[math]w'(u)^2+x'(u)^2+y'(u)^2=\Delta \tau^2 \left (\alpha^2+\beta_{x}^2+\beta_{w}^2\right )[/math]
Expanding this out gives us the following (I hit the max image size on this one):
[math]w'(u)^2+x'(u)^2+y'(u)^2=\Delta \tau^2 \left ( \frac{\left(\mathit{Vl}_w \left(2\, n+1\right ) + 2\, \mathit{Wl}_0\right)^2}{\left(2\, \mathit{Vl}_w \left(n+u\right ) + 2\, \mathit{Wl}_0\right)^2}+\frac{\left (\mathit{Vl}_x \, \mathit{Wl}_0 - \mathit{Vl}_w \, \mathit{Xl}_0\right )^2}{c^2 \left (2\, \mathit{Vl}_w \left(n+u\right ) + 2\, \mathit{Wl}_0\right )^2}\cos^2 \left(\frac{c \left (2\, u-1\right )}{2\, \mathit{Vl}_w \, \left (n+u\right ) + 2\, \mathit{Wl}_0}\right)+\frac{\mathit{Vl}_w^2}{c^2}\right )[/math]
Finally, we can substitute this result into the arc length integral and factor out [math]\Delta \tau[/math] (This is where the LaTeX image size is too big. We'll have to use the defined equations.):
[math]\Delta \tau \int_{0}^{1}\sqrt{\alpha^2+\beta_{x}^2+\beta_{w}^2}\, du[/math]
Now that we have the length of our path, we can derive the time dilation equation:
[math]\Delta \tau \int_{0}^{1}\sqrt{\alpha^2-\beta_{x}^2-\beta_{w}^2}\, du[/math]
I realized that I made a mistake when discussing the limits of these equations as the variable, [math]n[/math], approaches infinity. To explain this better, I will demonstrate the limits with the variable [math]n[/math] and with the variable [math]\mathit{Wl}_0[/math]. We need to use [math]\mathit{Wl}_0[/math] as our limiting variable because it is this variable that defines the initial radius of the sphere. Basically, we didn't need the variable [math]n[/math] because it was only used to align the cycles of the light clock which can also be done with [math]\mathit{Wl}_0[/math]. Thus, the variable [math]n[/math] and [math]\mathit{Wl}_0[/math] are practically the same except the variable, [math]n[/math], works in conjunction with the parameter, [math]u[/math].
Limits using [math]n[/math] :
[math]\lim_{n \to \infty} \frac{\left(\mathit{Vl}_w \left(2\, n+1\right ) + 2\, \mathit{Wl}_0\right)^2}{\left(2\, \mathit{Vl}_w \left(n+u\right ) + 2\, \mathit{Wl}_0\right)^2}=1[/math]
[math]\lim_{n \to \infty} \frac{\left (\mathit{Vl}_x \, \mathit{Wl}_0 - \mathit{Vl}_w \, \mathit{Xl}_0\right )^2}{c^2 \left (2\, \mathit{Vl}_w \left(n+u\right ) + 2\, \mathit{Wl}_0\right )^2}\cos^2 \left(\frac{c \left (2\, u-1\right )}{2\, \mathit{Vl}_w \, \left (n+u\right ) + 2\, \mathit{Wl}_0}\right)=0?[/math]
[math]\lim_{n \to \infty} \left (\frac{\mathit{Vl}_w}{c}\right )^2=\left (\frac{\mathit{Vl}_w}{c}\right )^2[/math]
Limits using [math]\mathit{Wl}_0[/math] :
[math]\lim_{\mathit{Wl}_0 \to \infty} \frac{\left(\mathit{Vl}_w \left(2\, n+1\right ) + 2\, \mathit{Wl}_0\right)^2}{\left(2\, \mathit{Vl}_w \left(n+u\right ) + 2\, \mathit{Wl}_0\right)^2}=1[/math]
[math]\lim_{\mathit{Wl}_0 \to \infty} \frac{\left (\mathit{Vl}_x \, \mathit{Wl}_0 - \mathit{Vl}_w \, \mathit{Xl}_0\right )^2}{c^2 \left (2\, \mathit{Vl}_w \left(n+u\right ) + 2\, \mathit{Wl}_0\right )^2}\cos^2 \left(\frac{c \left (2\, u-1\right )}{2\, \mathit{Vl}_w \, \left (n+u\right ) + 2\, \mathit{Wl}_0}\right)=\left (\frac{\mathit{Vl}_x}{c}\right )^2[/math]
[math]\lim_{\mathit{Wl}_0 \to \infty} \left (\frac{\mathit{Vl}_w}{c}\right )^2=\left (\frac{\mathit{Vl}_w}{c}\right )^2[/math]
We can see that by using [math]\mathit{Wl}_0[/math], we do not affect the equation for time dilation for the W axis in the previous post. I made this mistake because the correct variable to use was not easily apparent. This also brings us to the point that it is extremely important to check and recheck ones work often to make sure that you have derived the correct calculations : ) All things aside, we can now show the limit of this time dilation equation for the W and X axes:
[math]\lim_{\mathit{Wl}_0 \to \infty}\Delta \tau \left (\int_{0}^{1}\sqrt{\alpha^2-\beta_{x}^2-\beta_{w}^2}\right )^{-1}=\Delta \tau \left(\sqrt{ 1 - \left (\frac{\mathit{Vl}_x}{c}\right)^2-\left(\frac{\mathit{Vl}_w}{c}\right)^2}\right)^{-1}[/math]
We could derive time dilation for the Y axis, but the equations would come out the same as we have for the X axis. This is because all we have to do is rotate the path using the initial angles we have defined in the previous post. I do have the equations that consider acceleration. However, I will save that for a later post. Also, we can see that the limits of both time dilation equations are exactly the same as the ones I originally posted on page 1 post# 7:
[math]\Delta t_{r} \sqrt{1-\frac{V_{w}^{2}}{c^{2}}-\frac{V_{r}^{2}}{c^{2}}}=\Delta t_{n} \sqrt{1-\frac{V_{w}^{2}}{c^{2}}}[/math]
Next, we will begin discussion on the spiraling singularity. This singularity is not a gravitational singularity. It is a mathematical singularity. But, we will discuss this in the next post : )
I almost forgot that we need to derive the time dilation equations for the mechanical clock / rotating mechanism. We will discuss this after we take a look at the singularity. The reason for this is because I have only been able to work out the time dilation equation for the W axis. I will need to obtain a newer version of Mathematica (the one that uses the GPU to crunch) to solve the equation for the W and X axes because my computer takes forever to solve the equations and factor the results.
0 -
You are unstoppable uncool. Good job!!! I see I'm going to have to come up with an even harder challenge for you. Now let's see you crack part 2 of my second challenge : )
0 -
Mersenne Primes get the most attention because they do not require any calculation to generate the odd number to test. You just fill in an extremely large binary number with ones and then check for primality.
0 -
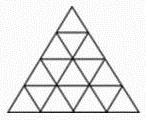
I know most of you have seen this problem at one point in time or another. The question normally wants you to count all of the triangles you see in the image. This challenge is not concerned with just counting triangles, but wants the equation which predicts the total number of triangles given [math]n[/math] number of rows.
The equation uses elementary operators and I will not accept a solution that is based on floor / ceiling, modular arithmetic, or piecewise functions / two part solutions. You must provide a single function which predicts the count of triangles given any number of rows. As with all of my challenges, I will give reputation to the person who can solve this problem before I post the solution within a couple of weeks : )
Sorry for all the edits to this post. My initial search on the internet did not reveal a solution to this problem. However, subsequent searches did yield a few solutions. Luckily, I did not find the solution that I have derived and I have modified the rules to narrow down the solution I am looking for. Most of my challenges were solved many years ago, before I had a computer. Back then, I worked most of these problems out by hand or with a TI-88.
0 -
To answer you question:
The point, [math]P(2 ,3)[/math] is produced by [math]f(x)[/math] such that [math]f(2)=3[/math].
You have been asked to find the corresponding point on [math]y=-3 \, f(x+2)-4[/math]. This means that the graph / function has been shifted to the left two units along the X axis, scaled by [math]-3[/math] and shifted down by [math]4[/math] units along the Y axis.
You can see that [math]f(x+2)[/math] shifts [math]f(x)[/math] to the left two units. So you have to set [math]f(x+2)=f(2)[/math] and solve for [math]x[/math]. This is done by setting the inputs equal to each other, [math]x+2=2[/math]. This gives you the corresponding X value which now equals zero. Ex. [math]f(0+2)=3[/math].
Since you know that [math]f(2)=f(0+2)=3[/math], you can solve for the corresponding Y value by multiplying the output [math]3[/math] by [math]-3[/math] and subtracting [math]4[/math] from the result which equals [math]-13[/math]:
[math]f(2)=f(0+2)=3[/math]
[math]y=-3 \, f(x+2) - 4=-3 \, f(0+2) - 4=-3 (3)-4=-13[/math].
This gives you the answer that you have:
[math]P(2, 3) \rightarrow P(0, -13)[/math]
I hope that helps : )
0 -
Very good uncool!!! Part 1 was easy. Now lets see if you can solve part 2 : ) I have confidence that you can do it.
0 -
It does have the interesting feature that -- with a slight modification -- you can make the additional part both continuous, and non-zero for an arbitrarily small region.
Very cool indeed! I'll have to explore your method in more detail. I give you props : )
0 -
Better than my solution, which I think is much more cumbersome, and a bit flaky as you have to assume positive square root.
[math]x^2 + \frac{1}{2}\left(1- \frac{(x - 3)^2 - 0.5}{(( (x - 3)^2 - 0.5)^2)^{\frac{1}{2}}}\right)(\pi - 9)[/math]
Also your rule of 'no trig' threw me waaay off of the trail of using (-1)^(f(x)) without prohibiting its use. Well done.

Thank you Schrödinger's hat. Your solution is interesting as well : )
0 -
We have a winner. Good job uncool!!! Except you didn't check the math so your answer didn't come out exact. But you did realize the solution : )
[math]f(x) = x^2 - (9 - \pi)*((-1)^{2^{((x - 3)^2)}} - 1)/2[/math]
=Uncool-
Your solution gave:
{1, 4, 18-[math]\pi[/math], 16, 25, etc...}
The solutions to alot of the problems I solve requires alternating sums. I realized that [math](-1)^x[/math] produces -1 or 1 whether the integer was odd or even. It didn't take me long to figure out that [math](1-(-1)^x)/2[/math] produces a 1 or 0. You can switch the one or zero pending on if you use a + or - :
[math]\frac{1\pm(-1)^x}{2}[/math]
After some thought I realized that by using [math]2^{x^2}[/math] as the exponent, the function would produce zeroes for all other integers except when [math]x=0[/math] which produces a one. The correct solution is:
[math]f \colon \mathbb{Z} \rightarrow \mathbb{R}[/math] defined by [math]f(x)=x^2+(\pi - 9)\frac{1-(-1)^{2^{(x-3)^2}}}{2}[/math]
1 -
What is 0^0 in this case?
Sorry uncool, [math]0^0[/math] is not defined and must be handled as an indeterminate form. This leads us to evaluate the limit of [math]0^x[/math] as [math]x[/math] approaches zero which would not produce the desired solution:
[math]\lim_{x \, \to \, 0}0^x=0[/math]
We could consider:
[math]\lim_{x \, \to \, 0}x^0=1[/math]
But, this would not produce the correct solution either.
The solution itself does not rely on Calculus and, as stated, requires only elementary operators such as addition, subtraction, multiplication, division, and exponents that operate on the variable, [math]x[/math]. However, at risk of giving away the answer, you are on the right track by considering exponents : )
To up the ante, I will give the person who solves this five stars and reputation if they do so before I post the solution.
0



explaining top 10 mysteries of the universe
in Speculations
Posted
That makes sense. Also, this would indeed increase the age of the universe according to your model because if inflation was correct, then this extreme expansion would shorten the "age" of the universe dramatically. This would mean that your model would predict stars / galaxies that are much older than the Big Bang prediction for the age of the universe. Is there evidence which shows such cosmological entities as being older than what the BB predicts?