Shadow

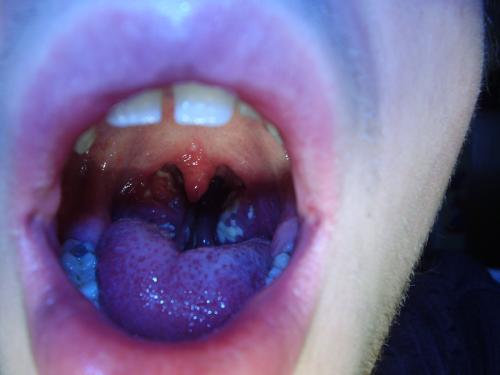
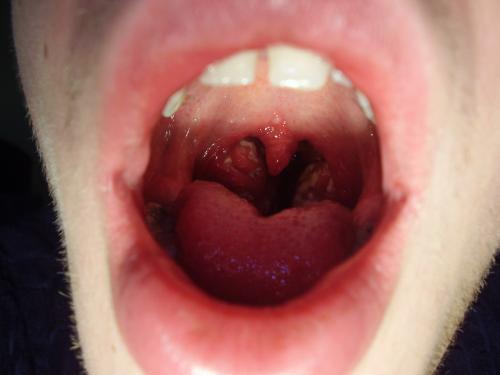
EDIT: My apologies mods, just realized there was a "Medical science" section, could you please move this post at your convenience? The following post in incredibly long, I know, but please, bear with me. I started being sick the Sunday before last; it started out as a barely perceptible sore throat which, over the next 24 hours, developed into a more serious one, accompanied by swollen lymph nodes. I went to have throat, blood and urine samples taken the next day, as I was suspicious of mono (my girlfriend contracted mono about a month ago and to be frank we didn't give much attention to the fact that it's transmitted by saliva. I was willing to take the risk, partly because I had been in contact with mono once before (drank from the same bottle) and was fine). I don't think I had any fever, no cough, just the cold I had been fighting for over a month. The only thing that happened was that multiple (maybe as many as ten) exceptionally sensitive cancer sores appeared in my mouth practically overnight. All the tests turned out negative; no mono, no tonsillitis, no strep and the cold turned out to be due to the fact that I'm allergic to something. So it was assumed it was a virus thing and I was instructed to rest and wait it out, which I only partly did; had a three hour course I didn't want to miss on Tuesday, work to be done for the course on Wednesday involving spending around two hours in a smoky room talking and then one quick trip through town on Friday to drop off some papers and talk about them with my supervisors (hour max). I was exhausted beyond belief every time, but spent the rest of my time in bed or sitting at the computer, reading etc. and actually seemed to be getting better. Then, on Sunday, I checked my throat just out of curiosity and found out my tonsils were covered in those white specks you get with tonsillitis (I don't know the official term for those and couldn't find a translation). So, I "called it in" (my doctor is also my uncle) and he prescribed penicillin tablets to take once every eight hours (specifically Penbene 1 500 000, phenoxymethylpenicillinum kalicum, although I don't know it that's a Czech version of the actual chemical, I couldn't find out much from a Google search). So, thankful that at least something had been found and I had a definitive way of taking care of it, I started to take the tablets. I followed up with the stupidest blunder I could have done; confident that my illness was taken care of and after researching marijuana and penicillin interaction, I smoked a joint (same day I started to take the penicillin - Sunday). I'm not sure how big an effect that had on the way the disease developed, what I do know is that it destroyed my throat (just pain wise), partly because of the munchies, for the remainder of the day and throughout the night. In the morning I woke up with my throat feeling like it was made from gravel, but a couple of cups of tee and oral pain killer tablets took care of that. I felt pretty much fine, and then around 3PM I got a huge fever, around 39.4°C, for like three-four hours. I took a multiple dose of fever-lowering pills and quite frankly I don't think they did much, but I was back to around normal by nine o'clock. After this episode, I was severely weakened until yesterday, partly because excluding yesterday and today, I haven't had a non-soup meal in close to two weeks, and only around two or three of the soup ones because it hurts when I swallow. I am now at the point where I can (sometimes) eat mashed potatoes, under the condition that I immediately gulp down water after every single mini-spoon-full I swallow. As I was told, antibiotics should start taking effect three days after the first dose. Except with me, penicillin didn't do a darn thing. If anything, I felt worse, although I can't say if that was due to penicillin directly or just it not having any effect and the disease progressing. Come Wednesday, I was pretty much desperate; I wasn't sleeping, when I did fall asleep for an hour or two I woke up drenched with sweat and my throat feeling like it was going to kick my backside for the ordeal it was going through; at times, it hurt so bad I had trouble ingesting liquids, although I always sort of got through that by forcing tee down, gargling salt solutions etc. My doctor/uncle swabbed my throat again on Wednesday (ie. three days ago); on Thursday, the results came back negative. Again. This confuses the hell out of my; my tonsil's where like balloons (still are), covered in that white stuff, my cold had turned into something where when I blew my nose in a specific way (which was/is majorly uncomfortable) this long string of mucus comes out, with a color similar to the inside of a pear (maybe a little darker) and blood usually mixed into it when it comes out in larger quantities. As it dries out, it becomes sort of gummy like. I haven't checked to see what happens next, I suspect it dries out completely in time. To add insult to injury, I also had/have mucus drainage from my nose into my throat which aggravates my tonsils all the more (in fact, I'm pretty sore it's responsible for 90% of my throat discomforts, because when I manage to completely clean everything up I'm absolutely fine, for like five minutes). Also, my lymph glands where still swollen, I still had the occasional fevers, couldn't eat. But according to the swab, there was nothing wrong with me. Being completely baffled by that point, my uncle took me to a throat specialist, who was as confused as he was; she eventually prescribed new non-penicillin antibiotics (this was last Thursday, three days ago) called Zinnat 500mg (Cefuroximum axetili). I've been taking those once every twelve hours ever since. My current condition: energy-wise I feel a lot better, although I think that owes mostly to the fact that I had my first real meal yesterday, but my tonsils are bad as ever (the white stuff has started to blend together; my grandfather (also a doctor) said that there's a difference, so I'm throwing it out here just to be sure). The white stuff is concentrated mostly on the left tonsil, while the right one is swollen more than the other (although both are swelled up pretty bad and both have the white stuff on them, see the pictures). I still have the cold, still occasionally come up with the gummy stuff although frankly my throat feels so destroyed that I rarely attempt to. A small cough has appeared as well, where I occasionally cough up mucus from my throat. My throat itself feels incredibly dry, even when I drink water, more than yesterday or any of the previous days. I'm still taking the antibiotics but they don't seem to be doing much, if anything at all. The cancer sores had mostly disappeared throughout the past week, some of them leaving red bumps in their wake which are painful at times. However, a couple of new cancer sores appeared a couple of days ago, although that might be a consequence of me not being able to brush my teeth real well due to the cancer sores themselves. I sometimes have pressure in my ears that I can't get rid of, although it's usually when my nose is completely stuffed up. Also the occasional headache. If there's a good soul among you who has come this far in reading the post; do you have any idea what I could be suffering from? I know there's no way in hell you can give me an accurate diagnosis over the internet, but I'm just looking for ideas, because of the two doctors and one specialist I have talked to, none have any idea what's going on and they're letting it show. And to be quite honest, I'm starting to feel pretty nervous about this whole business. I'm going to get my blood re-sampled on Monday, so I'll post the results once I get them, but that won't be until around Thursday. If you need any more information, go ahead and ask, I'll find out from my doctor. Thanks in advance for any educated guesses you throw forward.

I know this guy from The Teaching Company. He's really good.

That's next to impossible. Computers are such a wide field that it would be impossible to learn it all in one lifetime and that's ignoring the fact that new research is published every single day. On top of that, to understand computers in the way you seek, you would have to learn a good part of mathematics, maybe even all of mathematics...and that's definitely impossible. Don't want to get your spirits down, but in my opinion, we're just not alive long enough for the kind of thoroughness you're looking for.

http://www.learncpp.com/ - best online free C++ tutorial I know. Here are a couple of algorithm tutorial pages I found using a quick Google search: http://www.cs.berkeley.edu/~vazirani/algorithms.html http://www.topcoder.com/tc?d1=tutorials&d2=dynProg&module=Static http://www.topcoder.com/tc?d1=tutorials&d2=alg_index&module=Static Just copy/pasted from here. And here's one for math logic that came up in the alg. search: http://euclid.trentu.ca/math/sb/pcml/welcome.html - A Problem Course in Mathematical Logic Good luck

I made a similar mistake way back.

This will only work in MSVS, in other cases you have to #include <windows.h> This also means that the code won't be portable to other architectures. I usually use the following function (not sure if you've gotten as far as functions), although understanding how it works may be out of your grasp at the moment. But don't worry, as you progress in your learning you'll soon understand it easily: #include <ctime> #include <cstdio> void timePause(int seconds) { clock_t endwait; endwait = clock () + seconds * CLOCKS_PER_SEC ; while (clock() < endwait) {} } int main() { printf("And we shall wait for 3 seconds before the window closes..."); timePause(3); return 0; } -Source I think the best thing to do is to use the Code::Blocks IDE, which pauses the console by itself. And it's also great in debugging and quite frankly in every other regard as well, at least in my opinion.

Thanks Xittenn, much apreciated!

I think I gathered that from your first post as well as from searching the internet, but it doesn't answer my question; where do I start? I'm pretty much fluent in C/C++, so I'm familiar with the concept of programming.

Okay, that was quite a bit to take in. To be frank I think I'm even more confused than I was before, but that's to be expected. To quote the guy I talked to, I'd be "developing and implementing Cloud solutions". But I don't even know what that means and while that's just a quick Google search away, that's not what I'm after at the moment. I've long since been interested in learning more about this field since it has remained impenetrable for me for ages. But I've never had any motivation or reasons to delve any deeper, which is what changed in the past few days. But like I said, I don't know what half the stuff you mentioned means. I don't even know the name of the field I mention a couple of sentences earlier. The problem is that I have a very few terms floating in my mind right now with absolutely no connections to each other. To give a real life example, I know that pans are for cooking, the stuff that will be cooked is called food, the purpose of food is to be eaten, the process of cooking is achieved by raising the temperature of the food which is in turn achieved by use of the stove of which we have multiple types and all this takes place in the kitchen. I have no such framework in what I'm/we're talking about. I don't know the names, I don't know the relationships and I don't know what happens in the processes. And that's what I'm after; how to learn this stuff is step two, step one is what am I trying to learn? But thanks for your response, I wasn't sure if there would be anyone here who'd be able to answer my question.

I recently got an offer for a part-time job which would require me to learn PowerShell. Now, after searching the net a bit I gathered that for PowerShell to make sense, one must first be familiar with Windows Server (which is another thing I'm required to learn). Also, the word virtualization came up a number of times. The thing is, my knowledge in this area is limited to a very rough conceptual image of what ae server is and that's it; I can scarcely even host a CS LAN game. I'm eager to learn and I'm not limited by time, but I have absolutely no idea where to start. I tried searching for stuff like "Windows Server 2008 tutorial" but that just spews out a bunch of resources that build upon previous knowledge. I'm searching for something aimed at a complete layman, who has no experience with servers, networking or any of that stuff whatsoever, something that will allow me to build a knowledge base which will allow me to understand what Windows Server 2008 is, how it works and finally allow me to learn PowerShell, if possible for free. Any ideas?

Schrodinger's cat walks into a bar...and doesn't. Thanks Brian Malow via swansont. Another one I like: To get to the other side. Why did the tachyon cross the road?

Like I said, integral's are beyond my current knowledge (not for long though!) so if they're necessary to solve this problem then I'll just leave it be come back to it after I've learned integration. But out of curiosity I did try to evaluate the integral and solve the equation using Mathematica, and the result I get for [math]v[/math] is not the correct answer.

Except that I don't know [math]v[/math]; that's what I'm supposed find out in the problem. I'm aware of the fact that I can calculate it easily using simple trigonometry, but the whole point was to try and arrive at the answer using calculus, if possible; are you saying it's not? Also, I just used Mathematica to evaluate the integral and solve for v, since I haven't got as far as integration in my studies and was curious to find out if this method works, and the result differs from the one I get if I use geometry.

Oops, made a mistake; [math]\frac{d \Phi}{dt} = -\frac{v}{30(\tan(70^{\circ}) - \frac{v \cdot t}{30})^2 + 30}[/math]

Could you elaborate? I'm new to relativity and am not very good at deducing facts in physics, so I can't see the correspondance with the twin paradox I always thought that was just a concequence of himan perception...is there a name/term I could search for to find out more?

Or put differently, [math]a^2 \neq (a-x)(a+x); \hspace{1mm} a, \hspace{1mm} x \in \mathbb{R} - \{0\}[/math].

hypervalent_iodine and Blahah, you are both incorrect. Spyros, you're answer is correct; the guys above didn't notice you took the base 20 logarithm of both sides, not the natural/base 10 log: [math]36.65 = 20^n[/math] [math]\log_{20}(36.65) = \log_{20}(20^n)[/math] [math]\log_{20}(36.65) = n \cdot \log_{20}(20)[/math] [math]n = \log_{20}(36.65) \approx 1.202181[/math]

Thanks timo, that makes sense. Okay, so now I have to express the angle in terms of time, right? The only way I can think of doing that would be [math]\Phi(t) =\tan^{-1}(\tan(70^{\circ}) - \frac{v \cdot t}{30})[/math] which means that [math] \frac{d \Phi}{dt} = -\frac{v}{30(\tan(70^{\circ}) - \frac{v \cdot t}{30})^2 + 1}[/math]. What next? Is [math] t=10[/math] or [math]t=0[/math]? And how do I find [math]\frac {d\Phi}{dt}[/math]?

We've just started tackling relativity in our physics class, and there's a thought experiment I've come up with that I can't seem to resolve. Say you have an empty infinite universe, and in that universe are two objects, A and B, which are moving at some velocity relative to each other. Since there are no reference points except for the two objects, from A's frame of reference it is B that is moving and A that is stationary and from B's frame the opposite, ie. A is moving and B is stationary. Since time dilates due to velocity, in A's frame of reference B's time will be slower and from B's frame of reference A's time will be slower. But that can't be, since it would mean that time in one reference frame must be both slower and faster than time in the other frame. So which part am I thinking wrong about?

Hey timo, thanks for the response. I deliberately left the units out, just because I was lazy; I'm aware that units are very important in physics problems, but I didn't see any major role they would play in the mathematical perspective, so I just assumed the unit of distance to be "unit of distance" (ie. the cliff is 30 distance units high), the unit of time to be "unit of time" (ie. the whole scenario plays out in 10 time units) and the unit of velocity to be "unit of distance over unit of time" (ie. the velocity of the boat was circa three units of distance over units of time), since this was a mathematical problem, not a physics one. But for completeness, I believe the height was given in meters and the time in seconds, which would make the final velocity in meters per second. I thought [math]\frac{d\Phi}{dt} = -1 deg/s[/math] because the angle changes by ten degrees in ten seconds, although I'm still not comfortable enough with calculus to be sure that it can be calculated in this way; could you outline the difference between [math]\frac{d\Phi}{dt}[/math] and what I did, ie. [math]\frac{\Phi_1 - \Phi_0}{t_1 - t_0}[/math]? Really? Because I'm pretty sure I've seen plenty of examples being written something like [math]y = 3x+2[/math] and then [math]y' = 3[/math], which according to you should mean differentiation with respect to a variable called "y". Anyhow, [math]x'[/math] was supposed to denote velocity.

No one?

As for 1), I confess I haven't watched the video myself, but this might help you. I don't understand question 2), but that might just be a consequence of the fact that I know practically nothing of matrices. Just though I'd pitch in the video and hope it helps a bit.

I'm not sure I understand what you're asking, but I'll give it a shot; it's not "a plus and a minus give a minus", it's "plus times a minus gives a minus". Since you're adding two numbers and not multiplying them, it doesn't hold.

Hey all, we're reviewing trigonometry in our math class, and worked the following problem: A boat is moving at a steady speed towards the base of a cliff. At one point it is seen under an angle of 20° from the top of the cliff. Ten time units later it is seen under an angle of 30°. What is the velocity [math]v[/math] of the boat? We can solve this using trigonometry; if we denote the horizontal black strip [math]x[/math], the horizontal red strip [math]y[/math] and the whole horizontal strip (that is both the red and the black one) [math]z = x + y[/math], we have [math]z=30 \cdot \tan(70^{\circ})[/math] [math]x = 30 \cdot \tan(60^{\circ}) = 30 \cdot \sqrt{3}[/math] [math]y = z - x = 30 \cdot ( \tan(70^{\circ}) - \sqrt{3})[/math] [math]v = \frac{y}{10} = 3 \cdot (\tan(70^{\circ}) - \sqrt{3})[/math] Since I'd recently been looking at implicit differentiation and related rates problems I thought it'd be interesting to try and solve this problem using calculus, but the result I arrive at is completely different. Here is how I work the problem: [math]\Phi(t)[/math] is the function giving the angle between the cliff and the line connecting the boat and the top of the cliff at a certain time. [math]x(t)[/math] is the function giving the distance of the boat from the base of the cliff at a given time. We also know that [math]\frac{d\Phi}{dt}= \frac{60 - 70}{10} = -1[/math] [math]\tan(\Phi(t)) = \frac{x(t)}{30}[/math] [math]\Phi(t) = \tan^{-1}(\frac{x(t)}{30})[/math] [math] \Phi' = \frac{\frac{x'}{30}}{\frac{x^2}{900}+1} = \frac{30x'}{x^2+900}[/math]. We are interested in [math]x'[/math], we know that [math]\Phi' = -1[/math], so we still need to find [math]x[/math], which is where I think I made the error, since I don't know at what time I should calculate [math]x[/math]. I find [math]x[/math] by calculating [math]\tan(60^{\circ}) = \frac{x}{30}[/math], thus [math] x = 30\sqrt{3}[/math]. But, after plugging this value into the equation above, I get [math]x' = -120[/math], which is incorrect. So...where's the problem? Thanks.

Say I have an ideal coin, and I keep throwing it until I get heads. What would be the average number of times I would have to throw the coin? I'd say the answer is one; I'm not familiar with the terminology so I'll have to use my own words, but since the chance of getting either heads or tails is 50%, the number of times I get heads should equal the number of times I get tails (after an unlimited number of throws), which means that I can think of the outcomes of the throws as alternating between heads and tails. Or so I think.