ed84c

Thanks - I have very briefly, will have a bit more of a dig into it.

Hello Looking for someone to point me in the right direction so I can start researching a solution to the problem below: Problem Linear regression with high dimensionality - p=29, n = 5000ish, input variables are generally quite highly correlated When using the model for prediction, data sets regularly have a missing input parameter(s). At the moment I just refit a LSQ solution from the training data with that input deleted. This seems to lead to quite unstable results. Stability is important for my application, more so than absolute accuracy in some senses. -- Regularisation (e.g. Ridge) feels like it should help, but (and I'm not formally train in stats) as I understand that will reduce the variance of the model, with all input variables - and doesn't necessarily achieve anything for model stability where input parameters are deleted. Thanks in advance.

I was refreshing my memory of the derivation of ridge solution and realised I haven't got some of the intuition quite right in my head. Specifically - by using regularisation when fitting a very high order polynomial, intuitively the regularisation part of the objective function should kill off some of the higher order terms. However since the penalty is on the L2 norm of the weights, it will penalise larger weights preferentially and on first glance this would appear to penalise the lower order terms first. Since the data should be normalised this is not a problem in reality (ie. higher order terms in the data matrix are reduced, so their weights larger). But in that case by intuition would be the weight penalty reduces all weights at roughly similar rates, ie. unrrelated to the exponent. Hope that makes roughly sense ... any thoughts? Thanks in advance. Ed

The problem is the material properties of the tempered glass, as Iggy highlights, and as far as I remember bullet proof glass is layers of tempered glass (hard) and some sort of resin (absorbs the energy of the bullet). The tempered glass is cut to shape while still malleable and then cooled fast, the result is the outside forming a hard crust as the inside is still cooling and trying to shrink. This means that the outside is in compression whilst the inside is in tension. Now, glass has a fair large compressive strength but almost no tensile strength.As a result the outside will be hard but as soon as your bit tip enters the core and creates somewhere for a crack to propagate, the glass will shatter as the interior is in tension, which is where the glass is at it's weakest. That said, the world is full of clever people so it wouldn't surprise me if somebody has created some exotic method of machining tempered glass. Putting the glass under pressure might work I guess, that way you increase the compressive stresses throughout the glass (hydrostatic pressure will create pure compressive stress), which might mean that you don't have glass interior under tension that would otherwise shatter. Hope this helps/ makes some sense... Ed

Try looking for a PIR sensor. They are not too expensive. Most are designed for detecting intruders so can differentiate between 37Deg and ambient. I'm guessing if you dismantle it you can calibrate it to 65Deg and get it to give you a reasonable indication of the whereabouts of a hot object.

Thanks for the thought. Things have changed (like the amount of free time I have) since I was 15... but I'll be in touch if I need some advice again. Cheers mate.

These lecture notes are pretty good ,and the intro is a bit more gentle: http://www-control.eng.cam.ac.uk/gv/p6/ Lecture 2 is probably the most important to get your head around. Post again if any probs.

Thanks Timo

Question: Show that [math] {Ax = v_{0}}[/math] has no solution. I know [math] v_{0}[/math] is an eigenvector of A with eigenvalue 0, and the other eigenvectors do not have 0 eigenvalues. So, [math] {Av_0= \lambda_{0} v_{0}}[/math] [math] {Av_0= 0 v_{0}}[/math] [math] {Av_0= 0}[/math] So [math] {v_0}[/math] "is" the null space of A (since no other eigenvectors have eigenvalues of 0). So the question is asking me to prove there is no vector that when operated on by A gets to the null space. I can't think of how to prove this though, apart from saying "A operating on x can only give a vector that is 0 or in the column space"

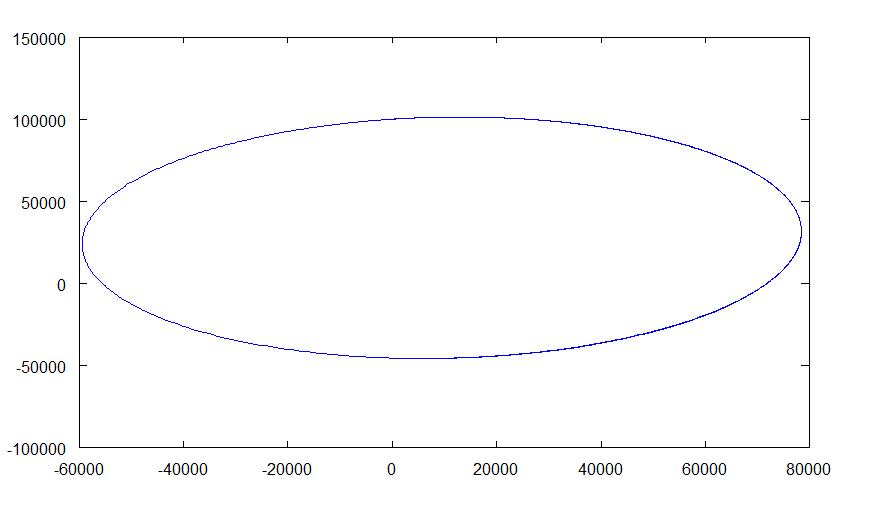
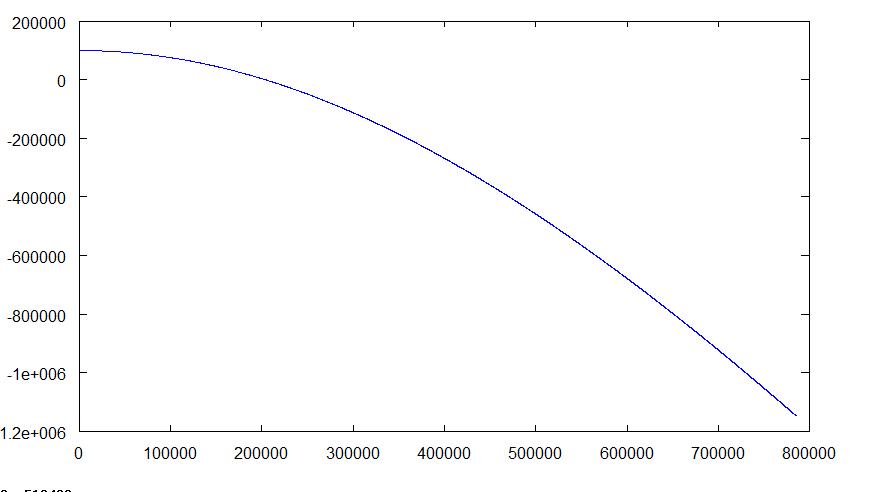
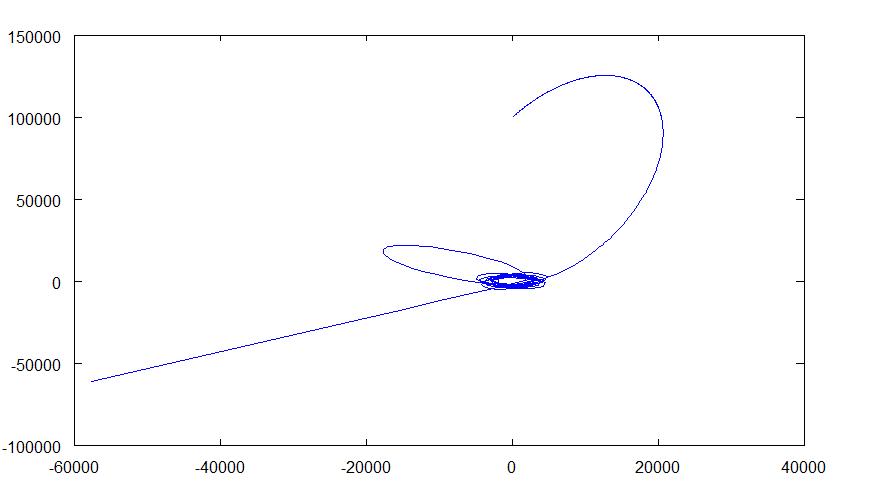
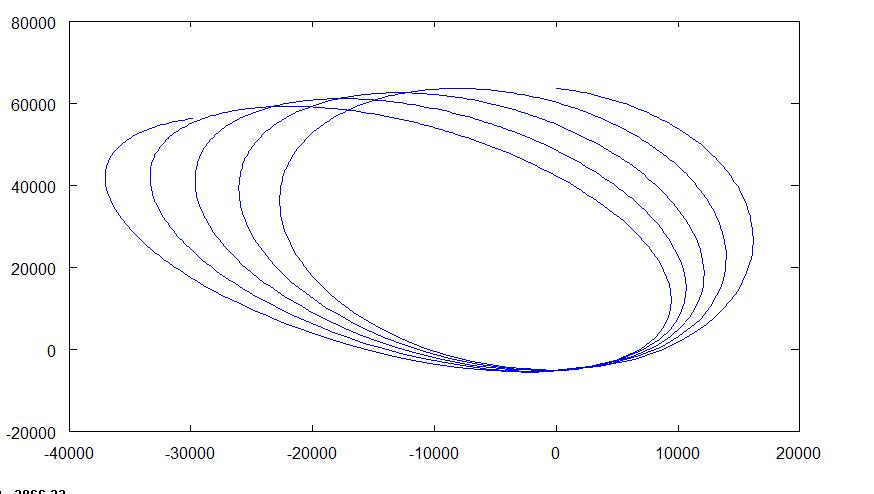
OK turns out it is working... sort of. My point was being sucked into the black hole and then the programme got upset and decided to spit it out creating a massive line that dwarfed the orbit before being "sucked in". However- the orbits still seem a little odd though- the origin of the black hole (0,0) is far too close to the elipse IMO. If somebody could take a look it'd be really good. I've attatched some pics and the altered code for a reasonable orbit. If you want to change the "starting velocties" change r and/ or rOld, in units of about 100- there is not explicit starting velocity that changes the tradjectory (it is effectively (r-rOld)/dt). You can increase the "length" of the orbit it is showing by changing t. Orbit2 (2).txt

Yup true. And I guess even if homework Qs arelooking for use of hyperbolics, it could be good practice to do it the long way round as you end up effectively deriving the equation for acosh,

I'm trying to write a Matlab (well.. octave) code to plot the tradjectory of a satellite in orbit. Unfortunately it just keeps drawing a diagonal line, but I can't for the life of me work out why it wont do any type of "proper" orbit. I think it's nearly there as if I "drop" the satelite (no tangental velocity) it does a sort of 1D elipse. I've attatched the file anyway (renamed .m to .txt as uploader didn't like) if somebody could have a look I would be very appreciative. I'm using the following to work out trajectories (given in question); [Math] r(t + \delta t) = 2r(t) - r(t-\delta t) + \delta t^2 * F(t)/m...............and....... \\ \\ v = 1/(2 \delta t)*x(t+\delta t) - x(t-\delta t)) [/Math] F, r, and v are 3D vectors for the Force, posion and velocity respectively. I'm plotting the x and z values of r(x,y,z)- to try and generate a loop, elipse etc of a 2D orbit. Orbit2.txt

My suggestion would be first to multiply through by e^x and move everything to one side (ie. you get ...... = 0). Then take a leap of faith as this this is a very similar function to solve to some you have been solving for years. (Hint: The answer to these is often = +/- .... likeyou have there)

Another good idea is to read through the manual thoroughly to work out what your chosen calculator is actually do and practice how to do it. Boring, and sounds obvious, but the number of times I've browsed a calculators functions weeks after the exam only to realise, "Damn! I didn't realise my calculator could do that automatically.."

I swore by graphical calcs all through high school and college (graphing is a great method for checking if answers are reasonable.) Unfortunately at uni they only allow 3 calculators (none graphical), but the best of these is definately; Casio FX 991 ES. Can do matrices, complex arithmetic, numerical integration and solve sim eq. and quadratics.... These functions are a great help if you are one of those people (like me) who in exams throw away 20% of their marks from doing a "2+2=5"....