md65536

2 hours ago, joigus said:

But flatness of the universe, as commonly expressed in cosmology books, seminars, etc., refers to spatial flatness. Not to Doppler effect. Doppler effect has to do with ratios d(tau)/dt; that is, proper time over coordinate time. It's, for lack of a better word, some kind of "time curvature". Flatness of the universe refers to flatness of the spatial sections of it.

Oops, I was thinking of gravitational redshift and often mistakenly call it gravitational Doppler shift. I was assuming that if there was a difference in the rate of time due to inflation, it would be due to a change in spacetime curvature. Can there be spatial flatness, but curved time, with a constant speed of light? Or would a changing rate of time require a changing speed of light? 

2 hours ago, joigus said:

Because the question stemmed from a post on "velocity of time", and you mention Doppler effect, I think there might be the rub. Does that make sense to you?

I think it does. I assumed "speed of time" meant rate, and interpreted it to mean "How would the rate of a clock now compare to the rate of the same clock shortly after the big bang (assuming the most general case possible)?" The more I think about it the less sure I am that it even makes sense to ask.

For example it makes sense to say, "I've aged one year less than my twin because of those two years (Earth time) I spent traveling when I aged at half the rate that I'm aging now," but this only makes sense with that second clock to compare to. In another frame, I'm aging at a half rate now, relative to some time I was traveling. Trying to "define things in a vacuum" as you mentioned, I was always aging 1 yr/yr and never aged slower. But then again!, I can just treat myself now and in the past as 2 different clocks and I can compare them, basically label my past self my "twin", and it's fine to say my past self in a different reference frame aged slower relative to me now, and for my past self to say "my future self will age slower relative to me now!"

But back to the case of inflation, I was thinking maybe it's possible to measure your own past clock relative to your current clock. For example if you could define a light clock where the only thing that changes over time is gravitational time dilation (is that even possible to do?), then there might be a red or blue shift occurring in the light clock over time. But how? For example you could make the clock inertial, and say it has 2 mirrors and you keep the mirrors relatively stationary throughout time. But if space is expanding during that time, keeping them stationary for one observer (you) means moving the mirrors according to another observer, so are you really making gravitational time dilation the only thing that affects the redshift? Anyway I got stuck without figuring that out. Without a way to measure it, I can't make sense of what it means to compare the rate of a clock in the past with itself now.

Using another clock to compare to is fine, the "standard clock" you asked for, but like you say: how? For example in flat spacetime in SR you can define a reference clock free from the effects of time dilation simply by making it inertial. But how would you bring a reference clock through an era of inflation without having it affected by it?

On 8/24/2022 at 7:37 AM, swansont said:

We know time depends [...] on your gravitational potential 

Gravitational potential is only meaningful in some simpler metrics like Schwarzschild.

Assuming our universe is flat on the largest scales, do we say it's flat because it has uniform mass distribution, and is that independent of the total mass? Then, assuming it's flat and that the big bang happened, theoretically it was always flat? Or is it flat specifically because it has very little average density, and wasn't always flat?

On 8/24/2022 at 8:42 AM, joigus said:

What is the standard clock against which time is seen to change?

If what I wrote above makes sense, you'd be trying to compare a clock in flat spacetime, to a clock in flat spacetime after inflation. Could it make sense to do it with a Doppler analysis? If you compared clocks at different places, the Doppler shift would mostly be due to inflation, but would there also be a gravitational shift over time even for a single inertial clock?

If gravitational time dilation requires curvature, and the curvature of the universe didn't change in general, then I would guess there's no measurable change in the rate of time for an inertial clock (in the general case) now relative to the same clock earlier, and no theoretical change either.

1 hour ago, Mitcher said:

To sum up, O is measuring an object moving along with O' at velocity v then, fair enough. But just earlier you wrote x and t can have any value; they are unrelated to v.

The transformation doesn't tell you what x and t are, you can choose that and it works for anything.

If you make t a constant, then x(t) can describe a single event. You don't need objects at all.

x = vt+r for a constant r gives you the world line of an object that is at rest relative to O' (the x coordinate changes over time, but x' doesn't).

x = r gives you the world line of an object that is at rest relative to O (the x' coordinate changes over time). x = 2vt is an object not at rest relative to either. x can be independent of v. So: no, there's no implicit object that is moving at v, it is the reference frame O' that is moving at v.

19 hours ago, Mitcher said:

we have x' = gamma.(x - vt). But v should be x/t, hence x = vt and we have x - vt = 0 which is meaningless.

With x and t being anything, the case where x=vt describes a particle that is at the origin of O' at time t, and the meaning of gamma(x - vt) = 0 is that a distance of 0 will always be 0 no matter what the length contraction factor, or in other words if two things are at the same place and time, you can't change that just by transforming their coordinates. Conversely if you have 2 events 1 m apart, you can transform to another coordinate system where they're 0.5 m apart. Eg. let x=vt+1 be a particle that is 1 unit (according to O) away from the origin of O', then x' will depend on gamma.

20 hours ago, Markus Hanke said:

Also, it might surprise you to hear that the law of conservation of energy exists only in flat spacetime - in the presence of gravity, things become rather more complicated.

In general and specifically in our universe, a frame of reference in curved spacetime is a strictly local thing, right? There's no global frame of reference that can be used to consider all the energy in the universe. The best we can do is say that for a local frame of reference, what we measure or predict is either consistent or not with the speculation that the total energy of the universe is zero. As far as I know, everything is consistent with it being 0, but there are too many unknowns that we can't measure, to say that it is so.

You can talk about the total energy of the universe, but not in terms of a frame of reference. So if you have a model where say the universe spontaneously comes into existence from nothing, and energy is conserved, and it ends up with curved spacetime and no global frames of reference, there are still ways to describe the energy of that system being 0, but it wouldn't be described using things like a conservation law that applies to frames of reference. There are different descriptions of energy, some frame dependent and some invariant. Is this right?

17 hours ago, mistermack said:

Didn't you post elsewhere that energy is frame-dependent? How would that match up with net zero?

You could choose a frame of reference where the entire universe has some great momentum, just by using an observer that's travelling at high speed relative to most stuff. It probably doesn't mean much to give a net momentum to the entire universe (because that's relative to what?). Or you could choose a frame where the universe has no net momentum. If you can do that, you can consider the "invariant energy" of the universe.

Adding to what joigus wrote, I think anywhere you are in the universe you can define an observer where, measured locally, the net momentum of the universe is zero? I hope this isn't a gross misrepresentation of GR. Basically, such observers everywhere don't share a frame of reference with each other, because space is expanding between them, but they're also not moving through space relative to each other, so they can each be "at rest relative to the local zero-momentum frame of the universe"... I think.

On 7/1/2022 at 1:47 AM, geordief said:

Ah,yes.Actually I hadn't actually  got round to  looking at it but yes it would be the gravity wells  depiction that I was after (but with the full-ish SR effects included -and "playable" ).

I imagine that at some academic or research level such simulations might  be in use  but probably not for the general public.

Well it depends on what you're looking for, a model that shows things in a simple way, or a rendering of what would be seen by your eyes. The movie Interstellar shows visual effects around a black hole, and I think they needed a lot of time on a supercomputer to render them.

In the SR game above, it doesn't include all the effects of SR, and yet the result is still confusing enough to the eye that you can't easily see what's going on. For Interstellar, they ignored the Doppler effect for artistic reasons. So even these are simplifications relative to what would actually be seen.

On 7/1/2022 at 12:21 PM, J.C.MacSwell said:

Can you now understand why it does not follow that "500 kg of mercury (a little less than 100L) will not float anything over 500 kg"?

Edit: I missed the double-negative and only now see I'm agreeing with you, but I can't find where/if the statement you're quoting was resolved in this thread...

How can you one possibly think that it follows, when you can do experiments in the kitchen sink with water and glasses that show that it's complete nonsense?

You're Others are forgetting (but it looks like mistermack pointed it out long ago) that the space displaced by the mass that you're floating, does not need to be filled with mercury! So for example, say you have 700 kg of mercury in a container, filled right to the top, and you put in a 600 kg weight and it floats, displacing 600 kg of mercury. This is acceptable, agreed? However, the 600 kg of mercury has spilled over the top, so now you have a 600 kg weight floating on 100 kg of mercury, in the space that can hold 700 kg of mercury.

Having tight seals or an "already floating" mass doesn't matter. If you have a stone sitting in a container that is just a little larger than the stone, you can float it using as little mercury as it takes to fill up the space not taken up by the stone.

On 6/28/2022 at 7:54 PM, md65536 said:

There's http://gamelab.mit.edu/games/a-slower-speed-of-light/

This demonstrates visual effects of SR by the way, not GR, and is not applicable to this thread. I wasn't paying attention to which topic I was in!

On 6/26/2022 at 4:54 AM, geordief said:

**perhaps "games" might be a better descriptor  as I was imagining that there could b quite a few settings to play around with.

There's http://gamelab.mit.edu/games/a-slower-speed-of-light/

It doesn't have a lot of options but it's built on an open-source Unity toolkit. The description says it shows time dilation (objects should be slower the closer you are to the speed of light) but I don't see it, and I also don't see delay of light (objects should appear faster as you approach them); it might be the effect is too small for me to notice.

1 hour ago, MigL said:

That is essentially correct, and depends mostly on the model being applied.
A classical point particle has no expectation of decay.
A quantum particle, which can decay, cannot be localized to a point, because of e the Heisenberg Uncertainty Principle, and the fact that, in QFT, the particle is simply a manifestation of its field.

Based on context and the forum we're in, the model must be a relativistic one. The quantum argument sounds reasonable but you can't make that claim about a gravitational singularity without a theory of quantum gravity.

1 hour ago, MigL said:

So what exactly would cause the transition to expansion/inflation ?

I don't see how lack of a clear cause is a useful argument. If you use that reasoning, you can claim that spontaneous particle decay can't happen at all.

1 hour ago, MigL said:

The actual universe is believed to have had a finite initial size, which was subject to quantum fluctuations, and may have initiated its expansion/inflation and subsequent structure.

Yes, it seems accepted theory is moving away from the idea of an initial singularity. My limited understanding is that the singularity is considered speculative, shown to be not necessary in some theories, and not possible in others. However the issue isn't settled because to do so would require a theory of quantum gravity. Therefore making claims as if it's settled, is speculation only. I haven't followed OP's arguments, I'm only addressing yours.

3 hours ago, MigL said:

A singular point cannot have any internal attributes that would cause it to become unstable, or inflate.

Why not? Are you implying that a point particle can't decay?

On 1/17/2022 at 5:12 AM, Genady said:

It might be easier to understand how it works by considering it in the vehicle's reference frame at the moment when it moves with the wind at the wind's speed.

At this moment, in the vehicle's RF, there is no wind, the air stands still, and the ground moves under the vehicle backward. This movement of the ground rotates vehicle's wheels. The rotating wheels rotate the propeller. Propeller pushes the air backward and the vehicle forward. This accelerates the vehicle and it starts moving relative to air.

In the ground RF, it starts moving faster than wind.

I think this is the key to understanding it. I also think most people's approach is not best, whereby they imagine a contraption and explain if or how it works. If instead you ask yourself, given that the air is still and the ground is moving at a constant rate relative to it, is it possible to extract usable energy from that? It's obviously "yes". It's obvious that it could be done without breaking the laws of physics. Then other misconceptions easily fall away too. How much energy can be extracted? Now what swansont said is obvious, you would want a bigger propeller to extract more energy (the more you let the ground pull, the more you must push against the air). It's obvious that the moving ground could provide enough energy to overcome friction in a well-engineered device. It's obvious you wouldn't want a weightless vehicle, if you need a downward force against the ground to capture energy from its motion.

Then, "How might that energy be turned into thrust, and does the device in the videos etc. conceivably do that?" is easier to think about.

On 1/16/2022 at 9:51 AM, exchemist said:

Hmm, do you mean that a glass prism gains mass if you shine a light through it?

On 1/16/2022 at 9:54 AM, Genady said:

No, I just mean mirrors. I take a box with internal walls being mirrors, let light in, say, through a little opening. Light just bounces inside from mirror to mirror (we can close the opening to make sure it doesn't escape). The mass of the box increased.

I don't think the light has to be confined, and a system consisting of a glass prism with light shining through it should have more mass than just the prism.

As a thought experiment, consider a massive particle at rest, and a photon moving with +x velocity. The photon has no mass, but considering the two particles as one system, this is not its rest frame. In the system's rest frame, the massive particle has some -x momentum balancing the photon's momentum. As a system, the particles' kinetic energy contributes to the system's rest mass.

Likewise the prism+light's rest frame would be different from the prism's rest frame. I don't know if this is meaningful in general, since spacetime curvature depends on how the mass is distributed, and I can't imagine how to describe the effects of unconfined photons. However there are cases where it is meaningful, such as with a "kugelblitz", a black hole created by a dense concentration of light energy for example.

23 hours ago, MigL said:

it expends the same amount of energy climbing out of a gravitational well irrespective of path taken, but depending only on the relative heights in the gravity well.

Yes, but gravitational potential is a Newtonian thing, and that applies (always) in a Newtonian analysis.

I was going to use gravity assist / planet flyby as an example of how an object can climb out of a gravity well using less energy, in a changing gravitational field. However, in Newtonian physics, the planet's gravitational force acting on the object equals the force of the object acting on the planet, and the object still uses the same energy to climb, it just gets it from the planet. So it's not the case that a dynamic system alone breaks gravitational potential's path independence.

GR is a different system, and I don't understand where and how the analogy to gravitational potential fails. But for example, I read that if you separate two masses, the GR analog to gravitational potential depends on if the masses are spinning, but the Newtonian gravitational potential doesn't.

On 12/1/2021 at 6:23 PM, Markus Hanke said:

 the volume implied by an entire bundle (congruence?) of such world lines should also be something everyone agrees on.

A light-like path has a geometric length of zero, so all events on a given light cone should have a geometric (hyper)volume of zero. The interior of the cone would have positive volume (by choice of convention) or a time-like volume. The elsewhere would have negative or spacelike volume.

The union of multiple light cones should have zero volume.* So for example if you have a light on the train, and turn it on at the beginning of the train's "life" and off at the end, then the geometric volume of all parts of the train that are lit over its entire life, is 0. If you consider only the lit part of the train (chop off everything outside the "light on" event's future light cone, and everything inside the "light off" event's future light cone), the train's entire existence has 0 geometric volume.

Am I thinking about that reasonably? If so, I'm not sure if an invariant volume would make sense. It seems like a long-lived train, treated as a bunch of time-like world lines, should have a time-like volume.

Or could you add up all the time-like world lines and get a different volume?

* Or... did I make a mistake here? Maybe you can't just add up two light cones, because there are space-like intervals between events on the different cones, but then there are also time-like ones... Now I really don't see what a geometric volume could possibly mean.

On 12/2/2021 at 3:25 PM, Markus Hanke said:

How so? Time dilation between two points would be a time-dependent function rather than a single value, since all of spacetime here is filled with gravitational radiation.

I mean between two events. I'm reasoning that if two clocks are identical except for their histories (basically, same place, time, and speed), they must tick at the same rate, and have the same time dilation factor relative to some distant clock. Therefore the time dilation factor between two clocks can't depend on "how the clocks got there" (I'm generalizing), yet a calculation of something representing gravitational potential, could.

13 hours ago, studiot said:

In your pursuit of gravitational potential are you interested in the application of 'the virial theorem' to cosmology ?

[...] If you want them the derivation is about 10 pages and also involves derivatives (or jacobians) of the Einstein equation and its solutions.

I've never heard of the virial theorem. It looks not basic enough for me. I should look at the derivation but I'd probably give up after getting lost at the top of page 1.

18 hours ago, Markus Hanke said:

As such it isn’t possible to assign a single unique value that signifies gravitational potential to any point in that spacetime.

But there is a unique single value gravitational time dilation factor between two points (in your example at least). Elsewhere on the web I see that gravitational potential represents the metric only as an analogy. Then the resolution might be that "gravitational time dilation is determined by the metric," while it's not always applicable that "gravitational time dilation is determined by gravitational potential"?

On 9/18/2021 at 2:23 AM, Markus Hanke said:

Correct - but with the caveat that the concept of ‘gravitational potential’ can only be meaningfully defined in certain highly symmetric spacetimes, such as Schwarzschild. It is not a generally applicable concept.

Resurrecting this idea, that I never ended up wrapping my head around...

Say we use a mountain as an analogy for an arbitrary spacetime. There's a clock at the top. Two travellers each transport a clock down the mountain along different routes, and meet at the bottom. There, they generally find their clocks have aged differently, but the two clocks, together at relative rest, are now ticking at the same rate. Their clocks tick at a different rate from the clock at the top, but of course the two clocks at the bottom share the same time dilation factor relative to the one at the top. Therefore there must be a scalar number that relates the two locations, that is independent of any differences in how spacetime is curved along the different paths between the two.

In this analogy, "height" works as that single scalar, and gravitational potential is meaningful. Is there another such scalar that relates two locations in an arbitrary spacetime, or is it just the "time dilation factor", and that factor isn't completely determined by any other scalar factor alone? Or, is it that gravitational potential loses meaning only where there aren't worldlines between the two locations?

Or to ask in a different way, if you have two particles in freefall with different velocities, that pass through some one event and later pass at some second event, is gravitational potential certainly meaningful along their respective freefall paths, and if so is it the same along both paths, no matter how asymmetric the spacetime is?

2*sqrt(2) cm is the length of the square inscribed in the circles, which should make it easier to figure out.

1 hour ago, Janus said:

10,000 meters in the track frame.  If the lightning strikes occur 100 m apart in the train frame, then scorch marks they leave on the tracks are 100 m apart as measured from the train frame.  Since the train measures the track as being length contracted by the same factor ( 1/100) as the track frame measures the train, then the proper distance between the scorch marks as measured from the track frame is 100m x 100 = 10,000 m.

Of course this means that the rear of the train ( being only 1 m long as measured from the tracks) reaches the point on the tracks where it and the tracks are hit by lightning while the front of the train is still 9,999 m short of where it will be struck by lightning, making the lightning strikes non-simultaneous in the track frame.

I agree. Interesting that you reasoned it out right from the start, and transferred the events from the train to the tracks, at rest in their frame. Was that essential to the reasoning, or just because that's what the question asked? (If I could redo the question, I'd make them ships in space without the tracks, but would that make the question harder to reason?)

Reciprocality should become pretty intuitive given the first postulate, it seems like a major prerequisite to understanding relativistic effects.

3 hours ago, Country Boy said:

You said that the train's "rest length" is 100 m.   Then in the train's frame of reference the two lightening strikes are 100 m apart.  Of course, in the track's frame of reference, the two lightening strikes are 1 m apart.

[...] I don't know what you mean by "abstract distance".  Any distance, pretty much by definition, can be measured, as well by a meter stick as any other way.

Yes, they're 100 m apart in the train's frame. The strikes / tunnel can't be 1 m in the track frame unless that 1 m expands to 100 m in the train's frame, which it doesn't.

Yes, I used 'abstract' incorrectly. It's the added object (like a ruler, train platform, extra tunnel etc.), used to conceptualize the distance, that's abstract.

Err, too boring? Or not intuitive enough? How about, "What proper length of tracks is contracted to 100 m in the train's frame, if the train with a proper length of 100 m is contracted to 1 m in the track's frame?"

4 hours ago, 34student said:

Is there one or more sizes of train in the frozen 3d universe at time = t* 

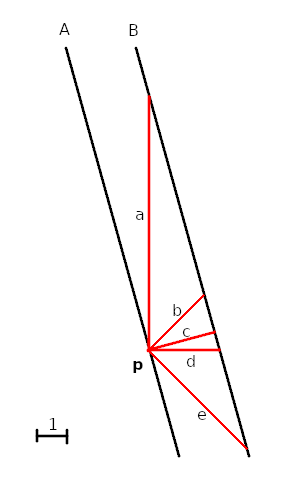
What is the length of a line segment that connects line A at point p, to line B? Is it one or more of a,b,c,d,e, or something else?

If line A represented the world line of the front of a train, and B the world line of the back of the train, what is the length of the train?

This doesn't even illustrate length contraction or the rules of relativity. I think you're missing some basic geometry in what you're asking.