md65536

The mass on a trampoline shows how paths of objects bend in a curved space. studiot, I don't see how your model shows that. The curved sheet doesn't technically need gravity to show this; distort the sheet some other way, and run a "straight" line of tape over the curve and the path will bend (analogous to a null geodesic).

Yes the analogy has problems. The mass represents mass, but the curvature is not representative of spacetime curvature, which I think is 0 at the center of the mass?* Showing the Earth resting on the sheet incorrectly suggests that it's the volume of matter displaces spacetime. I think this fails Einstein's "as simple as possible, but no simpler" criterion. Instead of saying "fabric", it could be called a manifold made up of events---would that stop people from asking what it's made of? Maybe the rest of the analogy could be fixed by labeling things similarly abstractly, instead of using concrete things like an Earth. But I don't know how you'd label it because I don't know what the curvature of the trampoline is actually meant to represent. Is it gravitational potential? Or is it just a toy example of an abstract curved space? I think the trampoline model could be set up and described differently, "no simpler than possible", so that it would both be clearer what it's meant to show, and not suggest other things. At the very least, I feel it should make people think something like "curved spacetime bends the paths of objects" and not "gravity pulls on the fabric of space" or whatever.

Speaking of space vs. spacetime, the inclusion of time in the curvature is what makes masses at rest gravitate toward each other (is that right? along with constancy of 4-velocity magnitude?) but I don't see how that could be represented on a curved sheet.

* Edit: now I'm confused because the curvature of the trampoline is also zero under the center of the mass, so maybe it does fairly represent curvature?

17 hours ago, Dagl1 said:

if they aren't at rest (both moving along line A-B at the same speed so that the distance between them does not change),

Maybe this was already explained better but I didn't see it. An inertial object is only moving relative to something else (ie. an observer). If they're inertial and their distance isn't changing, then they're relatively at rest. If you then say that they're moving at the same speed but still at rest relative to each other, then that's relative to another frame, which you haven't mentioned.

In non-relativistic physics, you might assume you're talking about some universal frame, but probably no one else here would do that; if you only mention frames A and B and then a speed, I think everyone would assume you mean A's speed relative to B and vice versa. You would have to specify a third frame ("Earth frame" for example) for people to get what you mean.

Also, an observer is a frame of reference in SR. https://en.wikipedia.org/wiki/Observer_(special_relativity) This is because you observe ie. measure the same distances and times no matter where you are in a given inertial frame, so you don't have to distinguish different viewpoints in the same frame as different observers.

17 hours ago, Dagl1 said:

If I move towards a star at 80% the speed of light, and I measure the distance to be 6LY, then if I moved very slowly towards it it would have been 10LY? And measured from the star, I too am 6 LY away when moving at at 0.8c, right?

The first part sounds right........ if the star is moving towards you at 80% of the speed of light and is 6 LY away, then you accelerate instantly so it is at rest, it should now be 10 LY away (not "would have". It still is 6 LY as measured in your first frame, and is 10 LY in your second frame).

The second sentence is kinda wrong and this is where it gets fun! You could ignore this until you get the rest of the replies in the thread. Because of relativity of simultaneity, you and the star don't measure the distance between you as 6 LY at the same time. For example if the star is 6 LY away, approaching at 0.8c, it will take 6LY/.8c = 7.5 years for it to arrive. But as observed by the star, your clock is ticking at a rate of 0.6x its own. So while you measure 7.5 years to reach the star (from the event where you measure the star being 6 LY away), the star measures 12.5 years in its own frame, during which you travel 12.5 y * 0.8c = 10 LY. The star measures you as 10 LY away when (according to you!) you measure the star being 6 LY away.

You also measure the star's clock ticking at .6x your own. You and the star are symmetric: each of you measure the other as 6 LY away at the moment (in your own frame) that the other measures being 10 LY away.

Or another way to see it is: at the moment (according to you) that the star passes the 6 LY mark on your rulers (which are at rest relative to you), the star's rulers are length-contracted by a factor of 0.6, and you are passing the 10 LY mark on its ruler. At the event where you say "we're 6 LY away", the star measures you at the mark that's 10 LY away.

... But then, you might also see, if you're at the 10 LY mark on the star's ruler and it's your ruler that's length-contracted according to the star, then when you're at the star's 10 LY mark, the star is at a 16.666 (repeating of course) LY mark on your ruler! According to you, the event of you passing the star's 10 LY mark is simultaneous with the event of the star passing your ruler's 0.6 LY mark. According to the star, the event of you passing its 10 LY mark, is simultaneous with it passing your 16.666 LY mark. This is no problem because the relative simultaneity of distant events is different for different frames of reference.

There are a lot of ways to describe this, I edited it to try to simplify, others probably have clearer and simpler ways to say it.

I'm assuming flat spacetime (no mass, SR only), and inertial motion unless specified.

12 hours ago, Dagl1 said:

If I have a map with the 'position' of different stars around the galaxy, or different galaxies in the observable universe, and we assume these bodies are moving at high speeds relative to each other, does the distance between two galaxies depend on the specific galaxy I measure these from?

Generally yes. Also "when are you talking about?" matters and is more complicated than a Newtonian description. The positions of things on a map are coordinates within a coordinate system, and those are different for different observers. You could have a map where the Milky Way is at a fixed location and Andromeda is moving, or one where Andromeda is fixed and the Milky Way is moving. Those correspond to the coordinate systems of 2 observers at rest in the respective galaxies.

12 hours ago, Dagl1 said:

If so then is there any 'absolute' distance between any points? Does it make sense to say that a star is x light years away, if by speeding up or slowing down, that distance is changed.

Yes, the distance to the star is different in the different frames of reference. There are invariant measures of distance, eg. the "proper length" of a 1 m stick at rest is always 1 m and everyone will agree on that, even if the stick is moving relative to some observer and is length-contracted ie. has a coordinate length less than a meter in that observer's coordinates.

12 hours ago, Dagl1 said:

I suppose the reason is that because galaxy B is in motion, we cannot say it is twice as far away from us, as we can only measure things from one frame of reference.

We can say that. We can measure the distances to both galaxies using one frame of reference (eg. the one in which we're at rest), and you can measure the motion of objects using the coordinates of that frame.

Consider the map analogy. The spatial coordinates can be represented by a grid drawn on the map. The same grid coordinates can be shown by putting a lattice of rulers throughout space. In our own frame of reference, our rulers are not moving and so they don't length-contract. An object light years away can wobble at speeds near c, but yet stay near one place in the grid of rulers.

Meanwhile, that distant wobbling object is moving relative to our lattice of rulers, and our rulers do length-contract, in its frame of reference. For simplicity consider two different inertial frames of reference F1 and F2 that the wobbling object switches between. Each of those frames has its own set of rulers making up a lattice throughout space, each at rest and not length-contracted in its own rest frame. Say I'm at 1 LY from Earth, as measured by Earth, and I'm wobbling relative to Earth. I stay near the 1 LY mark on Earth's set of rulers, but those rulers are contracted by different amounts in F1 vs F2. For example, in F1 Earth might be 0.8 LY away from me and the 1 LY mark, and only 0.6 LY away in F2's frame. The reason that the distance as measured by Earth isn't changing much, and the distance measured by me is changing drastically, is that I'm switching between different frames of reference. The distance between Earth and the 1 LY mark, which has a proper distance of 1 LY, is length-contracted by different amounts to different observers, depending on their relative speed.

51 minutes ago, Ant Death said:

Duration is as recorded by clocks and unique to each observer dependant upon change of position (distance) within the universe irregardless of the rate of change (velocity).

[...]

An inertial motion frame has a distance value greater than zero so duration values are less than time values.

[...]

Inertial light frame velocity = 299792458m/0s = infinite metres / zero seconds

You're making up definitions but it sounds like you're using "duration" to describe proper time.

You're not talking about velocity here. Velocity is a measure of distance/time as measured by a single observer (aka inertial frame). There is a measure of rate of motion called proper velocity or celerity that instead of measuring time using the observer's clock, it uses proper time as measured by the moving clock. Celerity approaches infinity as velocity approaches c. It's not a measure of velocity because you're measuring distance in one frame and time in another.

1 hour ago, Holmes said:

Classically, a point particle with a precisely located energy makes sense. With QM wouldn't such a thing require a completely undefined momentum, maybe other consequences? Wouldn't you need to start with a particle with infinite energy in QM as well? This example sounds like less of an incompatibility of the two, and more a problem of applying certain aspects of modern physics while ignoring others, and as expected reaching a conclusion that doesn't agree with measurements of reality.

On 4/28/2021 at 4:22 PM, Halc said:

So I think you mean rolling the paper so it intersects at a line following the time axis, thus forming a worldline of your stargate. Yes, you don’t need to distort the paper to do that. If you can create such a thing where the two gates are simultaneous in Earth frame, then you’ve created a time machine. All you need is a second set of gates that with the two ends simultaneous with the frame of some receding object. Go through the Earth gate, come back through the other one, and now it’s 1921.

Just pointing out that if you posit this sort of thing, then circular causality results. Didn’t need to accelerate either end of a gate to accomplish it.

[...]

You are opening a portal between events that are separated in a space-like manner. Nothing violated by that (except locality) until you open a second one synced in a different frame.

Yes, that's what I should have said, thanks for the correction. I was mixing up having a space and time coordinates drawn as a grid on the paper, and then mistakenly thinking of the paper as a space that exists in time. It should be the two worldlines of the respective ends of the wormhole, joined and then effectively sewed together.

As you hint at, and I argued in another thread, it wouldn't be enough to have two wormholes, with one going backward in time, to allow causal loops. The mouths would also have to be close enough together. There are no closed time-like curves if the curve is space-like. For example, if you go through a wormhole that brings you 100 years back in time, but also puts you 200 light years away, there is nothing at the entrance that you can affect before you leave. Or, if you travel far away "instantly" using one wormhole, and then back 100 year and ending up near Earth with another, but you have to travel 200 light years to get from one wormhole to the other, you also can't affect anything from before you leave.

On 4/28/2021 at 4:22 PM, Halc said:

Why would the gate time be synced with one end (Earth) and not the other? Wormholes don’t seem to have a preferred end like that.

I didn't mean they wouldn't be. The clock goes through at vanishing speeds. I was calling it "the Earth frame" but they share that frame.

On 4/28/2021 at 4:22 PM, Halc said:

Not sure how that can be construed as not entering until a long time passes. Ok, he not only steps through the gate, but does so at .866c. In that frame, he exits the gate at noon, and the receding Earth clock currently reads 9AM, which is 3 hours behind. So I read you so far. He’ll not enter that end of the gate until 6 hours from now when it’s noon over there.

Yes, that sounds like what I was thinking of. When I wrote "long time" I had the Doppler effect on my mind. But really, only relativity of simultaneity (3 hours) and time dilation (gamma=2) contribute to the long time, so let's say "it's a stretch" to call it a long time. The delay of light due to the (length-contracted) distance to Earth as well as the (not length-contracted) increasing distance of the Earth between the rocket's now and 6 hours later when it enters the wormhole at the other end, contribute to the much longer time until the rocket sees the Doppler-shifted image of itself entering the wormhole.

On 4/28/2021 at 4:22 PM, Halc said:

You are opening a portal between events that are separated in a space-like manner. Nothing violated by that (except locality) until you open a second one synced in a different frame. The main reason it isn’t a big problem yet is because you’re avoiding accelerating the ends, which is why I attempted to explore that part.

I wasn't thinking that far, I was only trying to describe the simplest case I could. But I guess you'd have to decide if the wormhole remains set up for the Earth frame, or if it behaves as an object that changes to a new inertial frame. In the paper analogy, eg. if you have 2 joined worldlines and you move them separately across the paper, do they stay sewed together like they originally were, possibly stretching and distorting? Or do they slide across each other as you skew the paper, and end up like they were set up for their new reference frame as much as they were for the old one? I have no thoughts on that, but I think that since this wormhole is not based on anything real or theoretical, you'd have to make it up.

On 4/28/2021 at 4:22 PM, Halc said:

The acceleration of the rocket doesn’t have any affect on what time it is back on Earth. You make it sound like a causal relationship when in fact it is just a changed choice of coordinate system, which can be done without actually accelerating.

Yes, I agree completely. I was only talking about "according to the rocket", meaning the coordinate time of the distant Earth in the rocket's standard (Minkowski?) coordinates.

The whole point is the acceleration doesn't have a causal effect, because the change in coordinate time on Earth when the rocket accelerates also corresponds with a change in relative simultaneity between the mouths of this wormhole. So for example, if two twins leave Earth and travel together "the long way" to the far end of the wormhole, and only one turns around (thereby having the distant Earth's time in their coordinates "jump ahead"), and they enter the wormhole roughly at the same time, they exit at roughly the same time too (travelling in opposite directions here). As in your example, they both age 2 hours while Earth aged 4, despite only one experiencing a change in relative simultaneity in its coordinates.

17 hours ago, Halc said:

You seem to be envisioning something like a stargate, a portal connecting the non-parallel worldlines of say two different planets.  If one thinks of it as such, there's no reason why it cannot look just like a window.  One can eat at a table that is half here and half there, and you can talk to the other person light years away as if they were in your presence, and can pass the salt and such.

Yes, that sounds like what I'm describing.

Another way to describe it is with paper. If you draw out gridlines representing time and one spatial dimension on a flat sheet of paper, that can represent flat spacetime, and the rules of SR can be applied. If you bend the paper without stretching it, you're not distorting the relations between events along paths drawn on the paper. The rules of SR still apply. The wormhole represents bending the paper and making 2 points touch, and adding a zero-length path or connection between those 2 points.

17 hours ago, Halc said:

If the clocks stay in sync despite the relative motion of ends of the wormhole, then one end can be accelerated as in the twin scenario, starting and ending in near proximity.  When the other end of the gate returns, the table is still there and both observers (neither of which have passed anything except the salt through the gate) will have aged the same, resulting in the wormhole/portal becoming a time portal instead of a spatial teleport setup.  In other words, the portal can be changed from connecting events with space-like separation to connecting events with time-like separation. Similarly, the stargate could be set up at constant separation but vastly different gravitational potentials.  If the clocks tick at the same rate, it quickly becomes a time machine.

If the two clocks do not stay in sync, the two parties eating at the table will have difficulty communicating since one will be 'faster' than the other.  The setup could be used to determine the absolute rest frame since the clock that objectively ticks faster must be moving slower. The principle of relativity would be violated.

I specified that the wormhole mouths are at rest in the Earth frame. It sounds like if you added the ability to accelerate them, you'd have a choice of what happens, and would have to further specify that?

As specified, a clock from Earth that goes through the wormhole at vanishing speeds at time t, comes out at time t. So the clock would remain synchronized with Earth's clock, in Earth's frame. To be consistent in other frames, the clocks would have to be out of sync in other frames. Let's say there are 2 clocks at either end of the wormhole, sync'd in Earth's frame. For a rocket traveling away from Earth in the direction of the far mouth, the clock on Earth is behind the one at the far mouth. In this frame, a rocket that enters at Earth and exits "right now" at the far mouth, will not enter until a long time passes! For a rocket travelling in the opposite direction, the rocket that exits "now" has entered a long time ago.

None of this is a problem at all. With the wormhole mouths not accelerating or changing their configuration, the rockets can communicate with each other. If a message can be passed in the Earth frame, it can be passed in any frame (light cones are invariant). Also, if a rocket exits and can say either "I have not yet entered the other side" or "I just entered the other side" or "I entered long ago", it can also switch between those statements simply by accelerating to a different inertial frame where another statement becomes true.

It sounds like, by underspecifying the wormhole details, I've made it possible to add details that violate SR, but it's also possible to leave it so that no added details violate SR.

So for example, say a rocket leaves Earth at high speed at Earth-time t and goes through the wormhole, exiting at local wormhole time t. But the time on Earth, according to the rocket, might now be t-0.6 years. The rocket turns around in negligible time. Local wormhole time is t+epsilon, but the time on Earth is now say t+0.6 years. It enters the wormhole at t+epsilon and returns to Earth at t+epsilon. Neither twin has spent significant time moving relative to the other, and both have aged negligibly. (This isn't any of the 4 scenarios above, all of which involve the rocket making a long-duration one-way trip.)

Or you could say, the rocket that exits could see Earth at two different times, one across flat spacetime, say .6 years in the past or future but the image delayed by ... a little or a lot by the travel time of light, and one at time t seen nearby through the wormhole.

The calculations I get are that

The wormhole I described is apparently not realistic. But, the same calculations can be done by removing the worm hole and replacing it with 2 planets on each end, with synchronized clocks, and then calculating a one-way rocket trip. You're then comparing the rocket's proper time and the Earth's coordinate time so it's not the same as the twin paradox, but that's fine, SR lets you calculate that. The wormhole is set up to connect events that are simultaneous in the Earth's frame, and an object traversing it in an Earth-frame's instant is sort of like saying that two clocks at either end and synchronized in the Earth frame, represent the same clock. It doesn't matter who goes through the wormhole or what their inertial frame is, the wormhole represents an instant jump in the Earth frame, generally not in other frames.

I wrote out a bit of time dilation and Doppler analysis for each of the cases, but it ended up being more tedious than I expected. I could post that if anyone's interested.

As usual, if you take out any magic or mystery from SR "paradoxes" and look at it geometrically, it's straightforward.

2 hours ago, Ghideon said:

My intuitive approach was to not look at the wormhole and just treat B's travel as a "Black Box" according to A. From the point of view of observer A the equations of special relativity should predict the outcome regardless of how B managed to travel. Or in other words; A should be able to apply the equations of SR to the flat spacetime in A's frame of reference and get a valid result. Or leave SR and apply other formulas* but that, in my opinion, deviates too far from the twin paradox  But I am not sure my approach is a correct way to try to apply SR in this scenario you have created.

That makes sense, to treat objects in the same inertial frame the same, regardless of what's in their black box. I think it would be easier to deal with proper time, because if you have the proper time of B between 2 points, then you really don't care what it does between those 2 points, or even if it remains inertial or has constant speed.

I think it doesn't work with coordinate time in this case. According to A, two different objects say B and B' that travel between the same two events, will age the same if they travel any path between the events at the same speed. By necessity, if they do that (same speed ending up at same place, regardless of what path they took to get there through a simply connected flat spacetime ie. no wormhole) then they'll have travelled the same odometer distance relative to A's inertial frame, for the same amount of time. But if B travels through the wormhole and B' travels through space, they can end up at the same location, with the same speed, and yet have travelled different distances. They couldn't travel different distances at the same speed and end up at the same event (same time).

The way I set up the wormhole, I'm assuming that B ages negligible proper time when traversing the wormhole. If B' makes the same trip through space at a speed faster than light relative to A, it should age a negative proper time I think.

5 hours ago, swansont said:

Doesn't a wormhole have curvature throughout its extent? It would seem odd to me if it didn't (but this isn't in my wheelhouse, so I could be mistaken)

I think it wouldn't matter, if it's possible to say "the proper time to traverse the wormhole is negligible", but I don't know if that's valid, eg. if what I described has a singularity. The relative time that passes outside the wormhole during the trip, is already specified. Effectively, if an object goes through the worm hole at Earth time t, proper time 0, they emerge at time t (in Earth's frame, aka. according to a local clock on the far end of the wormhole which is Einstein synchronized with Earth's clock) and proper time 0.

Basically, the shortest shortcut possible. That might be geometrically impossible for some reason I'm unaware of.

43 minutes ago, swansont said:

Approximately, I would think. (Once you have curvature I think you have to get infinitely far away to have flat spacetime, but you can say it's "flat enough" at some point where the time dilation between two points is negligible.) Like being far from a star and then passing by it, you would go from flat to curved to flat, as a first-order approximation.

I think you would have to know the details of what curvature the wormhole introduces as others have suggested or implied.

Oh, so any realistic wormhole would curve spacetime around the entrances, and with the Earth being nearby there would be gravitational time dilation for the entirety of the rocket's trips through space. I can see how that could change the answers of who ages more. I'd assumed no gravitational effects since none were specified. I effectively described an unrealistic wormhole, but I think it still works on paper.

31 minutes ago, Ghideon said:

From A's perspective B moves one lightyear in a very short amount of time (time much less than on year) and hence A uses a velocity v>c in the formula. The result contains the square root of a negative number since 1−v2c2<0  and hence SR fails in the scenario.

I didn't do it that way. You're using SR to try to calculate the time dilation while traversing the wormhole, but the description of the wormhole gives you that information. I'd say that B's velocity is constant relative to A the entire time, but there is a discontinuity in its location. However since location doesn't show up in that formula, it makes no difference. I don't think that B is actually travelling faster than anything by using the wormhole, it is merely travelling a shorter distance.

But I see what you mean, that was your answer! Yes, I agree it doesn't work to treat the travel through the wormhole as a really fast travel through the space between the mouths. It would have to be a path through a different part of spacetime.

5 hours ago, swansont said:

But curvature means that your location has a time dilation effect, which aren't described by SR.

SR assumes a locally flat spacetime, which you don't seem to have here.

Can you have a multiply connected flat spacetime with a bridge between two locations? I didn't specify that, so one could add other curvature if they want, but with a flat spacetime, SR describes time dilation while outside the wormhole.

But traversing the wormhole itself involves a singularity? Because of that, the time dilation factor is indeterminate? So it doesn't matter if it takes a negligible time to traverse the wormhole, because another clock might elapse an indeterminate amount of time in that instant?

I think that SR is not needed to describe the time dilation that occurs while traversing the wormhole, because I've given that information in the specification of the wormhole. I could post what I calculated for one of the scenarios to see specifically where this reasoning might go wrong, but I was hoping someone would have their own answer to discuss first.

20 hours ago, Ghideon said:

My reply is a quick intuitive answer and there may be more to your question than I realise at this time.

What is your quick answer? Maybe we could discuss it and fill it in more, and perhaps end up in agreement or learn about something we're both missing!

2 hours ago, Ghideon said:

I find your question interesting! I have not done the math to check this (yet) but I get a feeling that the wormhole introduces a scenario that special relativity does not adress. Does the formulas used to resolve the twin "paradox" apply when faster than light travel is possible? Can an observer, stationary relative to the earth, apply SR to calculate the time experienced by the twin travelling through the wormhole?  

My reply is a quick intuitive answer and there may be more to your question than I realise at this time.

I think it can be resolved with SR. Yes, the rules of SR still apply even if there are other aspects involved that it doesn't resolve, and even when there are aspects that modify the rules. Eg. if there's spacetime curvature involved, you don't throw out the results of SR, but neither does SR give you the complete answer. It's highly possible that my question is ill-posed! My intention was to describe the wormhole so that doesn't add aging effects that can't be described in the domain of SR.

SR can deal with faster than light particles, but shouldn't work for accelerating between faster and slower than light. However the wormhole is just a shortcut through spacetime. Basically it involves taking a shorter path between two events, shorter say than a straight path through flat spacetime that a beam of light might travel along, but it doesn't actually involve moving relative to something else at a speed higher than that of light. The situation above can break some physical laws, eg. it allows being in 2 places at once, but I think that on its own it's set up so that causal paradoxes aren't possible. The events here that an object can pass through "simultaneously" are outside of each other's light cones.

I guess "the time experienced by the twin travelling through the wormhole" would depend on the metric, and that would typically involve things outside of SR, but I tried to specify (not clearly?) that the proper time taken to traverse the wormhole is negligible. You should also be able to calculate some things based on being consistent with what some other observer sees. I may have missed something (ill-posed question) or reasoned wrong, but I came up with unambiguous answers that are consistent between observers. Yes, I'm curious about the intuitive answers! But more along the lines of intuitive reasoning, where you can convince yourself that you have an answer that the maths agree with, not just a guess. Also if you only have a guess, are there results from SR that can fill in the missing information?

10 hours ago, Kino said:

What's the metric of your wormhole? If you don't know that then the answer is "not enough information".

Does ds^2 = 0 make sense as a metric, describing a wormhole with negligible interior length and no other specifications? Or is it the external length (which I doubt because there's no requirement of external connections for general wormholes), something like [math]ds^2 = -c^2 dt^2 + dx^2 = 0 + (1 LY)^2[/math]?

I think that enough information is given, with the assumption that we start with the basic twin paradox and nothing more (so assume flat spacetime, no gravity etc.), then add just the wormhole information given (is that even possible while keeping external spacetime flat?). Wormhole traversal events are described; an object enters one location at time t and exits at the other 1 LY away at time t in Earth's frame. All other information can be determined because there is also the 1LY external connection, I think. Any other complications could be added if you want, and you get a different answer, but the same it true for the basic twin paradox setup. Have I oversimplified things to the point of nonsense?

8 hours ago, Kino said:

What's the metric of your wormhole? If you don't know that then the answer is "not enough information".

Is it not possible to describe a simple bridge between the two locations, assuming the simplest configuration without additional complications if they're not specified? Eg. no gravitational properties given, so assume no additional gravitational effects? No discontinuity given so assume it's continuous? The proper time needed to traverse the wormhole is negligible because its length is specified as negligible, right? This of course is a mathematical problem and not a physically possible experiment or anything.

What other information is needed? Is it a case where there are eg. gravitational effects that contribute to the answer and can change it by a lot, or is it that there are multiple possible wormholes that equally fit the inadequate description above, but have opposite answers to the question?

Consider a stationary Earth, with one end of a wormhole fixed nearby, and the other end fixed one light year away. The wormhole is a shortcut of negligible length connecting pairs of events, one at (0, t) and one at (1 LY, t). There are two twins, one on Earth and one in a rocket that travels at a relativistic speed relative to Earth (say 0.6 c or choose a convenient number). Who ages more in these 4 scenarios?:

1. The rocket leaves Earth, travels to and enters the far end of the wormhole, and ends up back at Earth, having been inertial the whole time.

2. The rocket leaves Earth through the near end, exits at the far end, and travels back to Earth, inertial the whole time. (How do these appear different, in terms of Doppler effect? Is there something here that you would say is "equivalent to acceleration" of the basic twin paradox?)

3. Suppose the same as (2), except that when the rocket exits the far end of the wormhole, it's moving in the opposite direction, and turns around (in negligible time) before travelling back to Earth. (How is this different from (2) in terms of measurements and/or what an observer sees?)

4. The rocket leaves Earth, travels to the far end of the wormhole, but it is the Earth that goes through the wormhole, and meets the rocket at the far end. (Is there an "equivalent to acceleration" here?)

I have guesses and explanations I can post later, but like before I'm curious about other people's answers and how intuitive relativity is.

2 hours ago, Halc said:

Still, Reissner-Nordström and Kerr black holes (and Schwarzschild) are not models of real black holes since none of those solutions include Hawking radiation.  Any BH has a finite life, and any events outside the past light cone of the final evaporation event will not be in the causal past of any event within the black hole.

Yes, exactly, so we can discuss what would happen or be seen in a particular model of a black hole, but must be careful not to make the same claim for just "a black hole" in general.

Having the universe's entire history in your causal past would describe a particle that is stuck on (or asymptotically approaching) some horizon, with a proper time that approaches infinitely slower than the rest of the clocks in the universe. That would be similar to an observer who could hover infinitely close to a Schwarzschild BH event horizon. So, EM repulsion exceeding gravity would make sense... it would be like the BH itself is causing you to hover (but this is inside the EH, so I don't think infinite energy would be needed?). I think the singularity still exists in those types of BHs, but with different geometry.

Looking for more details, I came across this:

Falling into the Schwarzschild black hole. Important details
S. Krasnikov

https://arxiv.org/abs/0804.3619

Quote

In Reissner-Nordström and Kerr black holes under their event
horizons (which are quite similar to Schwarzschild’s) there is another re-
markable surface — the Cauchy horizon. And that horizon does have the
property in discussion: an astronaut falling into the black hole reaches the
Cauchy horizon in a finite proper time and crosses it in a point p that con-
tains in its causal past the whole “external universe”. Such an astronaut,
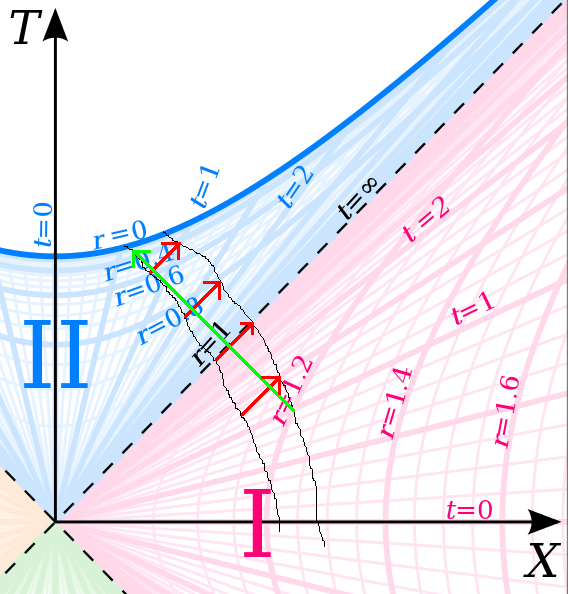
indeed, will be able to see the death of stars and galaxies,

which is surprising, but is a reminder that the details describing a Schwarzschild BH can be vastly different for BHs in general. The Kruskal diagrams are of Schwarzschild spacetimes.

1 hour ago, md65536 said:

you will lose sight of your feet eventually as the light cones narrow as you approach the singularity

This is wrong, as Kino wrote and the diagram shows. It seems you never lose sight of your feet, even if you dropped them in ages before the rest of you went in, but you'd also never see them hit the singularity (of course). You just see older images from when they were above where you are now, and there'd be a last possible image of them which depends on how long ago they entered, so I suppose they'd have to appear increasingly red-shifted.

3 hours ago, Kino said:

There is no invariant sense in which you can say that "your toes have now crossed" until your head also crosses, so you cannot report this. In your local inertial frame your toes do cross first, and you are free to report that your toes have now crossed (but others are free to disagree).

That's an interesting point. Indeed, "Earth" receiving your message in the far distant future would say "that never happened." If your head could at that point, separate from the feet and escape the black hole, it could go from its local inertial frame where the feet crossed, and return to Earth where the feet never crossed. That seems weird, but it's no weirder than the Andromeda "paradox".

Everyone here agrees one way or another that the head while outside the EH never sees light that originated inside, so nothing contradictory is measured by anyone (no observation of an event that can later be said not to have happened).

The astronaut saying "my feet have now crossed" is a red herring that suggests there is a paradox when there is none. Without that, the astronaut simply sees images of her feet from outside the EH while outside the EH, and from inside the EH while inside. The details are the same, but may be easier to think about?

9 hours ago, Markus Hanke said:

I don’t see how the eyes of the astronaut could possibly “catch up” with the photon, while still preserving the usual local laws of SR. Perhaps the answer is obvious (lol), I just don’t see it right now.

I think it's obvious if you look at it in terms of intersecting world lines and light cones. I don't know the calculations, but it's easy to see using diagrams of lightcones made by people who've done the calculations. Also, it's easier to think about what information is available to an observer, and not about how it would look. If the object's world line and an event's future light cone intersect, that object "sees" the event. Those are invariant and can tell you what happens without needing to describe it in a given observer's local coordinates. Because the coordinate speed of light at a distance inside the BH is not c, there's going to be visual distortion at some point, and you will lose sight of your feet eventually as the light cones narrow as you approach the singularity (before, after, or during the inevitable spaghettification?, I don't know), but that doesn't always need to be figured out.

3 hours ago, Kino said:

Here's a Kruskal diagram, copied from Wikipedia, with toe and head worldlines drawn (badly hand-drawn black lines), and a few light signals exchanged (red from toe to head, green from head to toe).

Interesting! The red lines show light from toe to head going from a lower r to a higher r outside the EH (pink), constant r on the horizon, and from higher r to lower r inside the horizon. A 45 degree line toward +X anywhere in those regions would have those properties.

1 hour ago, Markus Hanke said:

Consider an arbitrary event located directly on the surface in question, and attach a light cone to that event. Now look at the tangent space to the surface at that event. If the surface is like-like, the tangent space will fall to the interior of the light cone; if the surface is null, the tangent space will coincide with the surface of the light cone. So this isn’t the same - you can (at least in principle) escape from a light-like surface to infinity, but you can’t escape from a null surface.

But the future light cone interior is in the direction of the BH interior, that doesn't matter? Is it that the EH is a null surface, but also a light-like surface, yet the latter does not give you enough information to define the horizon?

1 hour ago, Markus Hanke said:

It depends what you mean by “nearby”. Since below the horizon the r-coordinate becomes time-like in nature, all light cones will be tilted inwards - meaning you cannot see anything that is below you, since it is impossible for a photon to increase its r-coordinate, irrespective of how it is emitted. You can still communicate with particles co-moving along with you at the same radial distance. A particle higher up than you can send you messages, but your reply won’t ever reach that particle.

My main argument in this thread is basically that you can see what is below you, because it doesn't involve a photon increasing its r-coordinate, but rather the observer decreasing its r-coordinate to reach that light. Is that argument wrong?

Inside the horizon, the r-coordinate of all photons must decrease over time. Near the horizon, the photons aimed "upward" decrease r very slowly. By necessity, an infalling object must decrease in r faster than some of its photons could---the object can't leave the future light cone of a past event on its own world line, and fall slower into the singularity than all of its light. This implies that an infalling particle can decrease in r faster than the "upward"-directed photons from events on the world line of an object below it. Thus, the infalling observer must be able to see objects that are always below where it is now, but were above where it is now when they emitted the light the observer is now seeing, which appears to come from below. In Schwarszchild coordinates (I think???) those photons are decreasing r very slowly, but in the observer's local coordinates they are moving upward at the speed of light. Just like the EH has a fixed r coordinate but locally moves past the infalling observer at the speed of light.

If this is wrong, I don't see how the astronaut could see their own feet, because their feet are at a lower r coordinate.

re. "The path of light that goes from feet to head also leads to the singularity."

3 hours ago, beecee said:

Can you explain this bit further in simple language?

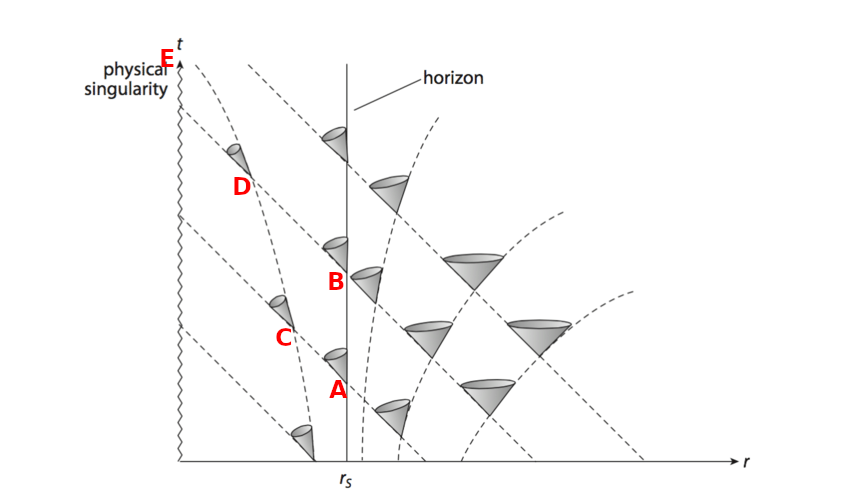
Sure, I'll use another diagram:

Here, the purple line could represent a path of light that goes from an event at the feet, and intersects the head's green world line, and ends up at the singularity.

The pink line represents light from an event, that is aimed 'directly' toward the singularity. It has a slope of 45 degrees, representing a coordinate speed of c. No object anywhere on this graph can have a slope shallower than 45 degrees.

Purple represents light from the same event, directed as close as you can get to away from the singularity. As you can see, it still reaches the singularity.

Blue represents all the locations at which light from the one event can reach the singularity, at different times.

Red represents an impossible object that "catches up to light" directed away from it. This is impossible, as has been stated a few times in this thread. No path can go from the right side of the pink line, to the left side of it.

Yellow represents some impossible objects travelling faster than light in the "opposite" direction. No path can go from the left side of the purple line to the right.

Green represents a possible world line for an object, that is traveling slower than light, and sees the event (when it intersects the purple line). Green could be the world line of the head. Even though it entered the BH after the feet, light from the feet can still reach it. Notice that at no point is there light moving away from the singularity. Notice that the possible paths for light from the event are not all the same, or same length. Their different slopes represents different coordinate speeds (in the graphed coordinates) of light. Inside the EH, all velocities in these coordinates are toward the singularity. The vertical alignment of light cones on the EH represents a coordinate speed of light equal to 0 for light directed away from the BH.

There is no "catching up to light" needed, because the light from the feet that intersect the head's world line is aimed *toward* the head, as well as toward the singularity.

1 hour ago, beecee said:

My limited understanding has me agreeing with MigL, for whatever that's worth.

MigL is simply wrong, using arguments that apply to a stationary or distant observer, applied incorrectly to an infalling observer.

We can all agree at least that it's possible to survive falling into a large enough black hole without tidal effects ripping you apart, correct? Writeups about this can be found everywhere with a simple google search. Is anyone arguing that those are all wrong?

What does it mean if you can survive falling through an EH intact, but you lose sight of your feet? You lose feeling from your feet, and your heart for that matter. You lose blood from your heart. You lose the half of your head underneath your eyeballs for that matter! What does it mean to survive intact, not be ripped apart by tidal forces, and yet be literally cut off from your body because light has suddenly taken on a completely different local behaviour?

2 hours ago, MigL said:

"At some point, the astronaut sends a message basically saying "My feet are now inside the event horizon", and Earth eventually receives that message."

IOW, he 'sees' ( gets information from ) his feet, inside the EH, and relays that information arbitrarily far away, to Earth.

No, you're purposefully neglecting that light takes time to travel from the feet to the head, about the same (in this scenario) time that it takes the EH to travel from the from the feet to the head.

This all implies the astronaut has a meaning for the use of the word "now". If the astronaut can say that the feet cross the EH "before" the head, then there is a meaningful point where it can say the feet are now inside and the head is not. If what the astronaut "sees" is also what the astronaut calls "now", then by necessity the head and feet passed the EH at the same time, and Earth does not receive that message. Either way, there is no paradox, there is no path of light from inside the EH to outside, and there is no point where the feet suddenly disappear because delay of light ceases to be a thing.

1 hour ago, Halc said:

Yes, the worldline would be through the center of a given light cone, not the edge, such as a line connecting A directly through D.  I think your head and feet need to be a little closer together to illustrate the light going from one to the other. There are no inertial worldlines in your picture.

I agree, that would be better. Wouldn't the shape and orientation of the light cones be independent of the motion of the light source?, while the shape of the source's world line would be entirely dependent on it. So not all world lines would be pointed locally along the axis of the cone. I think the image is a fair representation of the world lines of inertial particles entering the BH at near the speed of light, which is not at all what I wanted to show.

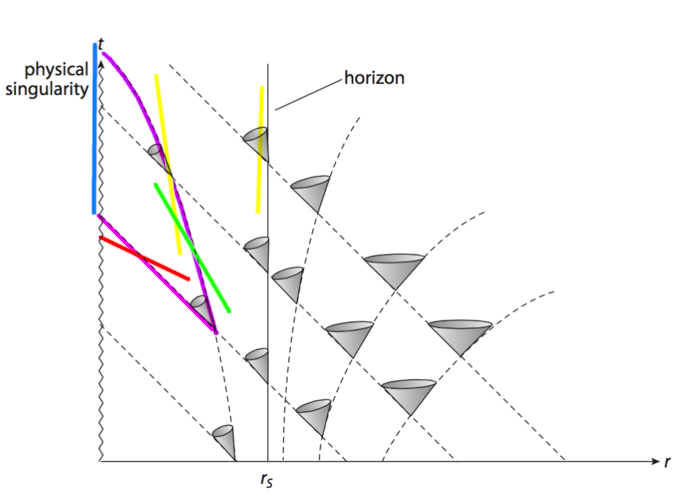
I've attached an image showing light cones inside the horizon. The labelled events are:

A - Feet pass the EH.

B - Head passes the EH.

C - Astronaut twitches her feet

D - Astronaut sees her feet twitch

E - Photons from twitched feet reach the singularity.

The scale of this is out, the astronaut twitches her feet in the short time before the head has entered the BH. More realistically, the head's world line would be very close to the feet's.

The light cones inside the BH show that light from a single event does not take the same amount of time to reach the singularity, in all directions.

Also... I think I made a mistake, the lines I'm using as the head and feet worldlines appear to be light-like. Can you see from the diagram as-is how it should look, or should I post a correction? Also, if you still think the head can't see the feet inside a BH, please show how this would look with light cones.

5 hours ago, JohnSSM said:

Time dilation dictates that time runs slower near massive objects.  With space and time being linked, how does slowing down time, also create an effect of a hole that is stretching space as you fall into it?

The slowing of time is only relative. An external observer measures the infalling clock slowing relative to its own, but the infalling observer measures their own local clock's proper time ticking at a rate of 1s/s. Their own clock does not stop as they fall into a BH.

If an infalling astronaut would lose sight of their feet, and smaller distances, this would imply that a light clock would stop functioning, or at least would stop depending on its orientation. Theory doesn't predict that.

5 hours ago, beecee said:

My understanding is as the two members above. Once inside the BH's EH, all paths lead to the singularity, so a person falling in feet first would not get to see his feet.

I'll throw something else in for debate...light/photons that are emitted just fractionally this side of the EH? All that light/photons not emitted directly radially away from the EH, will eventually arc back to fall into the BH. But any photons emitted directly radially away will always remain just outside the EH, never falling in and never quite getting away.

I really didn't expect there to be debate after a resolution was posted.

You still have light cones inside the EH, outside of the singularity. The cones do not become lines, where there is only one path for light from an event to the singularity. The path of light that goes from feet to head also leads to the singularity.

"Light beams aimed directly outward from just outside the horizon don't escape to large distances until late values of t." -- https://math.ucr.edu/home/baez/physics/Relativity/BlackHoles/fall_in.html but they do escape.

1 hour ago, Markus Hanke said:

It’s a null surface, actually.

Isn't that the same thing?

1 hour ago, Markus Hanke said:

The geometry of spacetime below the horizon is such that no stationary frames exist - in other words, no matter how much radial thrust the engines of the unfortunate ship put out, it will continue to experience radial decay as it ages into the future. So the two ships couldn’t remain at relative rest.

What did you mean by “paradox” in the thread title? 

Yes, but if both ships fell in, they could remain close enough to relative rest to not notice, for some time. Just like a person falling into a large enough black hole doesn't feel themselves being pulled apart for some time, even if tidal forces are always present (though negligible here). I'm talking about a black hole so immense that the gravitational effects are very weak at r_s, like an r_s of tens of billions of lightyears. If that's too small, maybe a billion times that! If you make it big enough, you should be able to continue falling toward the singularity for a lifetime without ever noticing you're trapped in a black hole. All the rules still apply, you can't communicate with anyone outside the EH, but the EH has expanded beyond you at the speed of light, and anyone you try to communicate with who hasn't escaped, is inside with you.

I can't say what would be observed on the inside of a BH, but my understanding is that accepted theory does not predict any strange local effects of crossing the event horizon, like suddenly being unable to communicate with or see "nearby" infalling particles.

By "paradox" I meant it's not a real paradox, just a conceptual problem to resolve.