Kedas

using a search engine would help, anyway... http://www.freshdevices.com/slide_show_software.html

For people interested in the problem some info here: http://www.math.jmu.edu/~jim/compressible.html

The model is based on this: (bottom page) http://www.engineersedge.com/fluid_flow/pressure_drop/pressure_drop.htm and also used here: http://www.cpvmfg.com/cat98/g-series15.htm

differential solution: (P(0)=Pstart=0) [math]P=Pin . Sin(\frac{Patm . t}{Volume.\sqrt{Kv}})[/math]

Thanks, Then my math model or my assumption of what will happen is the problem. It's about filling a tank with air. (y=tank pressure, a=inlet pressure. (dy/dt)=airflow) Does this mean that at a certain point the pressure in the tank will reach the applied pressure or is my airflow formula not good enough? (it seems logical to assume that it will never reach that pressure like a capacitor) formula in detail http://www.scienceforums.net/forums/showthread.php?t=20182

(I will talk about the second equation with a² because that's easier) Yes, I forgot about that part where y isn't defined. but there is one other thing I don't see: Dy is defined for y=a (Dy=0) but y should never get to that point 'a' since Dy reaches zero when y reaches that point. Just like the diff. eq. without sqrt, y will never reach 'a'.

If you solve this (Dy) = (a²-y²) with y(0) = 0 then y=a for t=inf (not periodic) y = a * (exp(2*t*a)-1) / (exp(2*t*a)+1) y= a * (F -1) / (F + 1) that sqrt is making it periodic somehow...

An other theory We know the position of what we feel by assocation. That kind of feeling corresponds to that location. touch/feeling, your senses and location are learned and stored. But what if there is something wrong with this data because it was wrongly learned. reasons for bad assocation/learning - Wrong learning due to bad functioning of the brain (tired,drug...) - And the difficult learnings like when two places touch each other what is the location of that feeling.

The first one

let's make it [math]\frac{dy}{dt}=\sqrt{a^2-y^2}[/math] [math]\int\frac{1}{\sqrt{a^2-y^2}}dy=\int dt = sin^-1 \frac{y}{a} = t[/math] so [math]y=a.sin(t)[/math] But this is still periodic, why is y not staying constant when it reaches a?

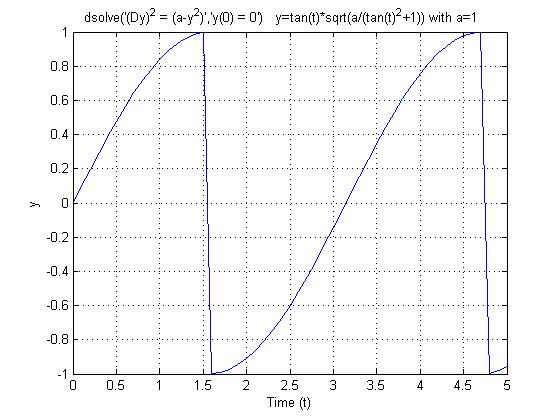
(Dy)² = (a-y²) with y(0) = 0 How do you solve this? Matlab gives these solutions: syntax: dsolve('(Dy)^2 = (a-y^2)','y(0) = 0') y=tan(t)*(a/(tan(t)^2+1))^(1/2) and y=-tan(t)*(a/(tan(t)^2+1))^(1/2) But these solutions are periodic if you look at the diff. equation: when y²=a then y should stay constant (not periodic) can anyone help?

How are you planning to avoid the interferance of natural selection? (You are not the only one making selections) It is possible that the natural selection compensates your selection. example: 1) a generation 2) you make a selection. 3) in the next generation all those that are closest to the first generation survive and those that are close to your selection die. So you can keep yourself busy for a while

I'm also sure you are not the only crazy person. I found there was in some case a link between the two points. In many cases you can make those two places touch each other. (by bending) This is most likely because the reason for the itch is easily shared by those two places. It is maybe possible that the itch is there on two places but only one is noticed by the brain until that itch is gone. And if all of this is wrong then you are just crazy

The jar is cylinder shaped. (so forget about all other shapes) It gives you almost 8000 ton air. - It is 324m (not 300m) - 1ton=1000kg. (SI)

Seems to be correct, I did some fast calculations and it could be right due to its big ground area and very small top. http://www.tour-eiffel.fr/teiffel/uk/documentation/structure/page/chiffres.html

So all we have to do is separate information from energy(states) so we can transfer information wihtout transferring energy.

h(m).density(kg/m³).g(9.81m/s²)=pressure (Pa) 1mmHg=0.001*13500*9.81=133Pa or 0.133kPa (Redfox was right about that)

After you convert the numbers you also change the unit. like 12/8 kPa. What is the problem?

I have this diff. equation: [math]\frac{dP}{dt}=\frac{Patm}{Volume}\sqrt{\frac{(Pin^2-P^2)}{Kv})}[/math] with Patm, Volume, Kv = constant; P = Tank Outlet Pressure; Pin = Tank Inlet Pressure I would like to have a laplace function of this so I can use it easily in simulink, this way I can put many air tanks behind each other. Isn't there a way to go to a laplace form, skipping the diff. equation problem. Matlab solved the diff. equation in a way I don't like: simplify(dsolve('DP = Patm/Volume*sqrt((Pin^2-P^2)/Kv)','P(0) = Pstart','t')) like this: F=[sin((Patm*t-atan(1/(Pstart^2-Pin^2)*(-Pstart^2+Pin^2)^(1/2)*Pstart)*Kv^(1/2)*Volum................. Matlab gives up when it has to make a laplace of this. any help is appriciated, thanks

I travel to the future every day. I get the train in the morning to go to work and at the evening I return home with the train. Didn't I just travel to the future? because my house has experienced more time than I have. OK it's not a big diference but it is there.

So we can go to the future because it hasn't happened yet?