Everything posted by JeffJo
-
problem with cantor diagonal argument
Because M is defined to be the totality of all possible elements E. Why does he not mention M in: This is the construction of the list that is diagonalized. All it comprises, are elements defined like the element E. Not the "totality of all possible elements E." What diagonalization proves, is that any list of elements from M, necessarily omits at least one element of M. It never claims to use, or to not use, all of M in this proof. +++++ The problem is that it is taught incorrectly. More than just claiming to use real numbers, which it works on but Cantor did not use. The first line in most teachings is something like: Assume, for contradiction, that you have a list S of every real number in [0,1). ... when that first line should really be: Let S be any list that can be made from just real numbers in [0,1). What is usually taught is invalid as a proof by contradiction (I'm not saying it is invalid, just not a proof by contradiction. You have to use every part of what you "assume, for contradiction, that...". And what is taught does not use the "every" part of that contradiction. It just proves it is not "every." But students have it hammered into their heads that it is the archetype, so they remember it. How about Bertrand Russell's version? It's very close to Cantor's, but in English, with more modern math terms:
-
problem with cantor diagonal argument
I try to represent things consistently, rather than how you use inconsistencies to misrepresent Cantor. You are co-opting the notation used by others, maybe in the hope of creating confusion. One example of such confusion is the "diagonal" that you think is an important property in CDA. It isn't defined, or even mentioned. I am being consistent with the notation used in Wikipedia: A capital letter represents one of the sets being used, while a lower case letter represents one of the strings that is a member of these sets. That makes it easy to recognize how the indicies are being used. The letter S is used for the set that is subjected to CDA, and s for its members. The letter T is used for the set of all eligible strings; that is, Cantor's M. No, the point is that CDA only works with sets that that are known to be countable. They are subsets of the complete set T (or Cantor's M), which is not yet known to be countable, or uncountable. Before the proof, your M0 and M1 are also not established either way. So this argument you are trying to goad me into has no implication on CDA. This is where you misrepresent Cantor. He never claimed that E0 (what Wikipedia calls just s but I prefer s0) was not in M (what Wikipedia calls T). He said it was not in the sequence E1, E2, E3, ... ." Cantor never names this set, or calls it a subset of M, but he does define it in a way that means a subset. You are trying to exploit this by misusing his symbols, and misquoting Cantor. When I say that S is a subset of T - and note that "subset" means a relationship between two sets - I mean only that every member of S is also a member of T. It can be a proper subset ("incomplete or partial") or an improper subset. The only properties I reference are that every member of S is in T, and that all members of S are represented in a list s1, s2, s3, ... . This is what Cantor meant when he said "If E1, E2, …, Ev, … is any simply infinite series of elements of the manifold M...". He doesn't explicitly mention a set that is equivalent to my S, but he also never says "all elements of the manifold M." So, by definition these Ev's comprise a subset. What you are missing (either deliberately because it contradicts your arguments, or by omission because you don't want to look at what might contradict it), is that Cantor never says his E0 is not in his M. He says the exact opposite: "then there always exists an element E0 of M, ...". Where he says E0 can't be found, is in the sequence: "...which cannot be connected with any element Ev." I am confident he knew exactly what his statements meant. But either you don't, or you don't want to admit that you do since it contradicts yous arguments.
-
problem with cantor diagonal argument
Keeping it relevant (see P:"It's possible you have a problem in comprehension." J:"It's obvious that you don't want to comprehend CDA."), which of your two sets. M0 or M1, is one where you know that the conditions Cantor placed on the set S hold true?" That is, the Ei's in these conditions: If E1, E2, …, Ev, … is any simply infinite [einfach unendliche] series of elements of the manifold M .... If you can't show that either M0 or M1 can be put into such a list, then any answer to your question has no significance to CDA. But the answer is s=0000... can be in subset S0 of M0 that can be put into a list as Cantor requires. There are listable subsets S0' that do not have s=0000... as a member. s=1111... can be in subset S1 of M1 that can be put into a list as Cantor requires. There are listable subsets S1' that do not have s=1111... as a member. Now, if you will stop trying to change the details of CDA to fit your incorrect criticism of it, we can discuss why it is a valid proof. But if you continue to misrepresent it, we can't. Whether or not you interpret such writing correctly (you don't), they have no bearing on the mathematical proof called CDA.
-
problem with cantor diagonal argument
I suspect there are German words that mean the following, but I only know a little German ("he's sitting over there" - the movie Top Secret). But this is why I use '0' and '1' as the characters. Take '1' to mean "true" or "included." Take "0" to mean "false" or "excluded." Then each Cantor String - a function of the form C:N->{'0','1'} - defines a unique subset of the natural numbers by including or excluding its position number. CDA is not a formal proof, it is an example, using infinite sets, of Cantor's Theorem that the power set of any set has a greater cardinality than that set. It's obvious that you don't want to comprehend CDA. You want to misinterpret it in your failed attempt to disprove it. I fully comprehend the parts of your argument that are comprehendable. Most aren't. And I use C:N-->{'0','1'} in place of E. This is a properly-define function that map every natural number n to one of two characters. The set M (I often use "T" go be consistent with Wikipedia's article, but I don't recall if I have done so here) is the set of all such functions. On the contrary, every E he uses is a function, as I showed. He didn't define the ones used in CDA, he defined the conditions they must satisfy. Cantor never compared N to his set M. This is a common misconception, but it is a misconception. And if you have read the actual paper, this statement alone proves that you did not "comprehend" it. You don't even get all the words right. Cantor says that there are subsets of M that can be put into a one:one correlation (he means a bijection, while "correspondence" means an injection). This is true, there are trivial examples like "all '0' except a '1' in position n." He goes on to prove that any example that can exist misses at least one member of M. He does no such thing. Those three strings were examples of what the strings in M can look like, not the beginning of the CDA proof. He hasn't even presented the proposition that CDA proves at that point in the paper. Which is: 3. "If E1, E2, …, Ev, … is any simply infinite series of elements of the manifold M, then there always exists an element E0 of M, which cannot be connected with any element Ev. This "begins with" a set of E's - not the totality of all E's which comprise M - that has the property that it is in a bijection with N. He does no such thing. Nothing like your "D" is mentioned in the paper. He does no such thing. There is nothing "random," tho it is "arbitrary." The proof "begins with" any ordered list E1, E2, ..., Ev, ... that can exist. Each Ev is defined in this list, but "arbitrary" means that the actual definition doesn't matter. Because Cantor never mentions "diagonal," never defines a "diagonal D," nor a "45º angle." He defines a new function where E0(n) = 1-E(n,n). Later Mathematicians interpret this as a diagonal, but that term is not mathematically defined in the paper, nor is it pertinent to any part of the proof. This new function E0(n) = 1-E(n,n) fits my definition of a Cantor String C:N->{'0','1'}, so it is a member of M. Ignoring the fact that this quote has nothing to do with CDA, so it is irrelevant to CDA, you fail to "comprehend" it. You just don't like what it means.
-
Clouds changing color inside rainbow arch
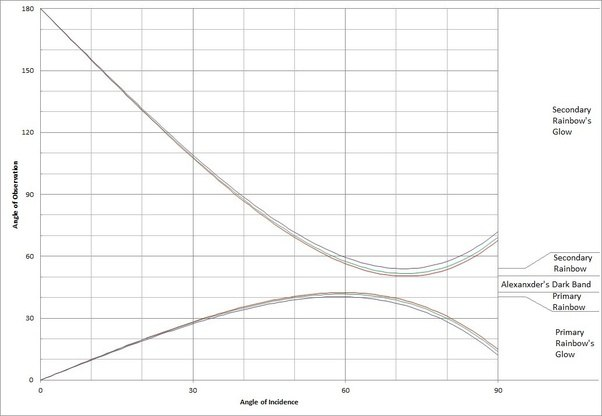
Why? There is nothing "partial" about separation. But the term applies to individual rays, not the entire reflection. It is total in individual rays. But at most observations angles where a reflection is observed, every color of light is observed in that reflection. No, the equation refers to the angle of deflection. That deflection is caused by two transmissions (refraction accompanies transmission) and one reflection. And it references Snell's Law: Well, since I mentioned that explicitly, yeah. A cross-section of it is displayed in this diagram that I repeat: The "red" reflection is a 42 degree wide, filled-in circle with a bright rim. The "violet" reflection is 40 degree wide, filled-in circle with a bright rim. Other colors do the same in-between. The 2 degree difference is caused by aberration, not separation. The specific angles are caused by the fact that the equation you didn't see Snell's Law represented in has a maximum at about A=60 degrees and D=40 to 42 degrees. Not because other colors "separated from" the violet light the eventually deflected 40 degrees. It is an example of dispersion, which means the equation evaluates differently for different colors, not the they spread out.
-
Clouds changing color inside rainbow arch
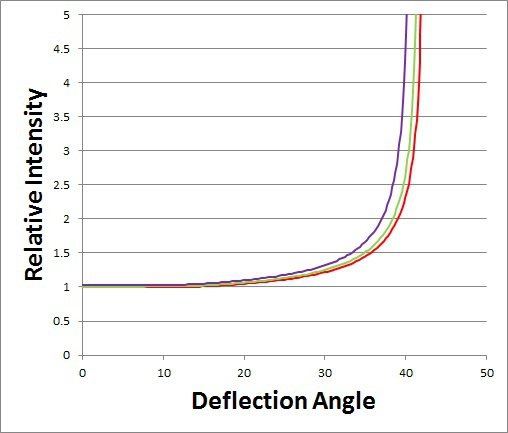
And I described it. It determines the angle B in the equation D(n)=n*180°+2*A-(2n+2)*B, where A is the angle of incidence of an incoming light ray, n is the number of (not total) internal reflections, and D is the total angle thru which that light is deflected. Since the primary and secondary rainbows are both seen when looking away from the sun, often this is subtracted from 180° and put in the range 0° to 180°. That's 4*B-2*A for the primary. "Dispersion" does not mean colors separate, it means that each color's optics have to be handled separately. That is, each gets a different curve in plots like this: The ranges of deflection angles that I labeled the "glow" is where no separation of colors is observed. (Yes, it still occurs to individual rays, but the colors recombine). The Calculus of Rainbows shows how to determine the "rainbow angle" as a function of k, the index of refraction. For the primary, the angle of incidence for the incoming ray is A=arcsin(sqrt((4-k^2)/3)) = 59.48° for red light with k=1.3318. For this ray of red light, B=40.30°, and D=4B-2A=42.24°.
-
problem with cantor diagonal argument
Why? It is you who are in denial. First off, I'm not quite sure you understand what the sets are. As evidence, "any set of binary symbols" seems to be a vacuous description. Cantor's set M (as opposed to whatever you think M is) is the set of all possible Cantor Strings (my name). A Cantor String is a function C that maps the set N of all natural numbers, starting with 1, to the set {0,1}. (Well, Cantor used {'m','w'}, but any difference is insignificant.) We can write this C:N->{0,1}. Any individual character in this string can be expressed as C(n), for any n in N. Cantor's Diagonal Argument does not use M as its basis. It uses any subset S of M that can be expressed as the range of a function S:N->M. So any individual string in this function can be expressed as S(n), for any n in N. And the mth character in the nth string is S(n)(m). So the diagonal is D:N->{0.1} is the string where D(n)=S(n)(n). By definition, this is a Cantor String, so it is in M. And the negation of it, D', is the string where D'(n)=1-S(n)(n). And it also, by definition, is in M. What isn't necessarily true, is that either D or D' is in S. D may or may not be, but that is irrelevant. D' cannot be, because D' is different than every S(n) in the nth position. No, he did not. You did. Cantor defined functions of the form C:N->{0,1} and showed that D' fit that form. How the characters are extracted from the 2D table used to illustrate it has no significance.
-
Clouds changing color inside rainbow arch
And those images overlap almost entirely. While "separation" - the word I used, and that is used most often - implies they don't. Diverge: "to move or extend in different directions from a common point." The vast majority of the reflection consists of white light, comprising all visible wavelengths. The overwhelming interpretation of rainbows (basis for this statement: Newton's "colors of the spectrum" are almost never called that, they are called "colors of the rainbow") is that each band is monochromatic. All I'm trying to get across, is that they are not. But those who learned it that way seem very reluctant to accept that it is wrong. Never. I said that the result "separation of colors" is not observed. That is not synonymous with "refraction," which means that the ray tracing has to be handled separately. This isn't that complicated, unless you intentionally try to misunderstand it. <Sigh.> As does the process I described. I expressed it with Snell's Law. As they do in the rainbow reflection, inside the violet band, even after two refractions have affected the light. Again: the split occurs to individual rays. Most recombine with the other colors, from incoming sun rays that hit the drop at a slightly different place. And yet again: the split occurs to individual rays. Most recombine with the other colors, from incoming sun rays that hit the drop at a slightly different place. No, in the area where the colors recombine, it brightens the sky. Alexander's Dark Band is actually unaffected. See step 1.2 of my outline of the process.
-
Clouds changing color inside rainbow arch
Do you understand that "internal reflection" means only "reflection inside an object," and really has no special significance beyond the geometry? But that "total internal reflection" has a very specific meaning, and does not mean (although it often does) being inside an object? When light encounters the boundary between two transparent media, some reflection always occurs, but transmission does not always. If the angle of incidence is greater than the critical angle, C=arcsin(1/k), no transmission occurs. This effect is responsible for fiber optics, the sparkle in diamonds, and the optics in binoculars. It's also why aerated water looks white, as total internal reflections occur on the outside of the bubbles. I never said that internal reflections are not responsible for rainbows. I said that total internal reflection is not. But I usually try to say "reflections inside" so that I don't cause the kind of misunderstanding you seem to have. Even if it was just a habit to add "total" in front of "internal reflection," it is still wrong and teaches the wrong things. I have no idea what "problem" you think I have. And they offer the same explanations that I have. But not yours. They do not support "the light leaving the droplet has been split into diverging blue and red rays with the blue above the red" as the cause of a rainbow. It isn't the "diverging rays" that cause the rainbow, it is the fact ranges of the deflections are different, as a function of wavelength. And that's what "dispersion" means. That ray tracing is a function of wavelength. For single rays, colors separate. For the entire image, aberration occurs.
-
Clouds changing color inside rainbow arch
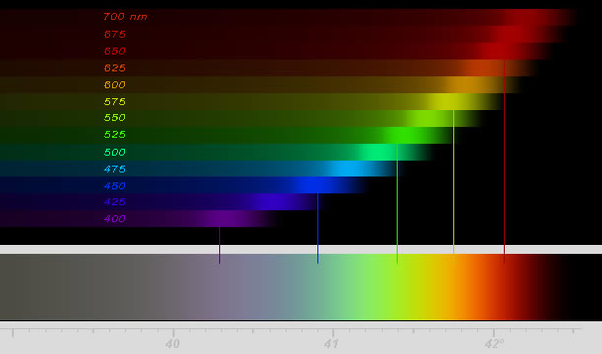
That was an obvious typo, and editing restrictions prevent me from changing it. It (quite obviously) should have been "refraction." No, it does not. Reflections only invert the "depth" dimension. And if reflection did invert them, the colors would be seen in the same order. The primary rainbow is a filled-in circle that is centered on the sub-solar point, with an angular radius of about 40° (violet, inside) to 42° (red, outside). The secondary rainbow is a similar filled-in circle that is centered on the sun, not the sub-solar point. It has an angular radius of about 126° (violet, inside) to 130° (red, outside). This means that the image "wraps around" the top of the sky, and is seen about 10° above the primary rainbow. The colors are in the same order, inside-to-outside. But because it is seen upside-down, "inside" is higher than "outside." This relative order is caused entirely by the magnitude of the deflection angles, and the alternating center (sub-solar point, sun), not the number of reflections. If the index of refraction were on the order of 2, the secondary rainbow would be seen the side of the sky with the sun, with red higher than violet. I can show you the equations that lead to these results. There are no total internal reflections, so there can't be a second one. Perhaps this is a typo, too? If you accept "total internal reflection," "reflections invert images", and "the rainbow is a spectrum," then I can see why you don't find them unacceptable. But it seems that Indian schools are quite fond of teaching rainbows, as many of the explanations you will find come from there. I'd say 90% get it wrong. Maybe you should look at this site, if you think UK information is better: https://atoptics.co.uk/rainbows/primrays.htm . It is actually one of the leading sites that give entirely valid information.
-
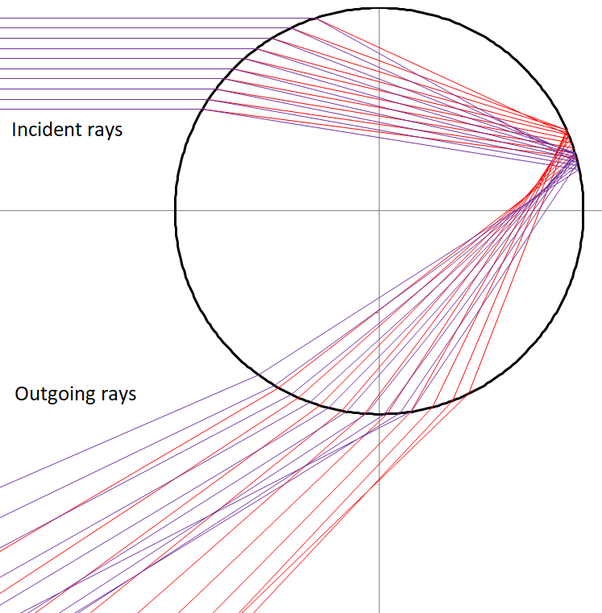
Clouds changing color inside rainbow arch
Some light always reflect off an air-water interface, in either direction. See Fresnel Equations. However, little light bounces off of the outside, and it scatters in many directions. But strictly speaking, I didn't explicitly state whether the rainbow comes from light that reflects off of the inner, or the outer, surface. You read "outer" into what I said, ignoring the diagram that shows internal reflections. All that I said is true. The only things making my statements difficult for you to see were my attempts to not go into detail, and your unwillingness to accept it (which I infer from the fact that you ignored my ray diagram showing internal reflections.) But here's a more detailed explanation. See the ray diagram if you find it unclear: Say a ray of light strikes the surface of the drop making angle A with the surface normal. 0°<=A<180° Both transmission and reflection will occur. But the reflected light is dim, and uninteresting. Most of the light will enter the drop with angle of refraction B=arcsin(sin(A)/k), where k is the index of refraction of water. 0°<=B<C, where C is the critical angle where total internal reflection occurs. The total deflection is A-B. Note that the line containing the surface normal passes thru the center of the drop, so it contains a radius. This light will pass thru the drop, and make angle B with the surface normal at the back. It is angle B because the ray makes an isosceles triangle with two radii of the sphere. Many explanations for rainbows say total internal reflection occurs. It is impossible, since B<C. Both reflection and transmission occur, and again most transmits. The light that exits without ever reflecting does not form colored rainbow bands, but does make what is called the "zeroth-order glow" around the sun. The light that reflects is deflected 180°-2*B. Step 2 repeats, in theory, indefinitely. But the amount of light that reflects becomes insignificant after a few internal reflections. The light that exits has an angle of refraction of A. The total deflection is again A-B, and the sign of this angle is correct. The light that exits after n internal reflections has a total deflection angle of 180*n+2*A-(2n+2)*B. For the primary rainbow, it is customary to subtract this from 180 since you look away from the sun to see it. This is what I plotted above.
-
problem with cantor diagonal argument
Maybe you should come back when you learn to read. He didn't need to imply what he wanted to prove, he stated it explicitly. "[In 1875] there appeared, probably for the first time, a proof of the proposition that there is an infinite manifold, which cannot be put into a one-one correlation with the totality [Gesamtheit] of all finite whole numbers 1, 2, 3, …, v, …, ... However, there is a proof of this proposition that is much simpler." And you should at least attempt to understand what the words you ignore mean. A infinite list is, by definition, a set that is in a bijection with the set N of natural numbers. That means it has the same cardinality (oops, you left that one out), not a greater cardinality. He wanted to prove that the cardinality of M was greater, not "an infinite list/enumeration of sequences contained in M." Maybe you should read the .pdf you linked, without your pre-existing bias. I call your attention to the section titled "Cantor's method", in the paragraph following figure 1, line 4: "for all v in the set M." But "v" is the index of the columns, while he meant the index "u" of the rows. D has the single coordinate u. It is a function whose domain is the set of natural numbers, and whose co-domain is {'m','w'}. The set M is the set of all functions whose whose domains are the set of natural numbers, and whose co-domains are {'m','w'}. So by definition, D is in M. That is, it is an "E".
-
problem with cantor diagonal argument
Yeah, I have several Quixotic causes where I try to un-convince people who are convinced of an incorrect solution. Another here is the explanation of rainbows that is almost universally taught, yet contains errors of fact and interpretation.
-
problem with cantor diagonal argument
I have read it, without preconceptions. It is very confused. Maybe you should read Cantor's proof without your preconceptions. From the pdf: "He [Cantor] concludes E0 differs from D for all v in the set M" No, he concludes that E0 differs from Eu for all u in the list that E0 was derived from. Neither "v" nor "u" are in the set M, they are natural numbers not binary sequences (rows). What Hudson calls "D" is the diagonal that is negated to get Cantor's E0. Both are in M, by the definition of M. And nothing described as "all <whatever> in M" are referenced in this part of the proof. The rest of the paper refers to constructions that have nothing to do with this conclusion, so they are irrelevant. Whether or not "A different random list could contain E0" is irrelevant, since any list you can produce can be used to construct a different E0 that is not in that list. And the point is really quite simple: The actual diagonal argument does not prove that M is uncountable, it proves: IF you have a list of sequences from M, THEN we can construct a sequence that is in M, but not in this list. In "analyzing" this proposition, there is no reason to refer to "all M," or any other sequences besides 00 derived from the list in hand. But once you have the truth of this proposition, it "follows immediately" that M itself is uncountable.
-
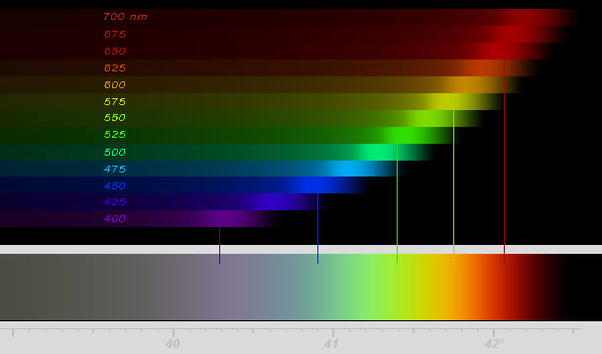
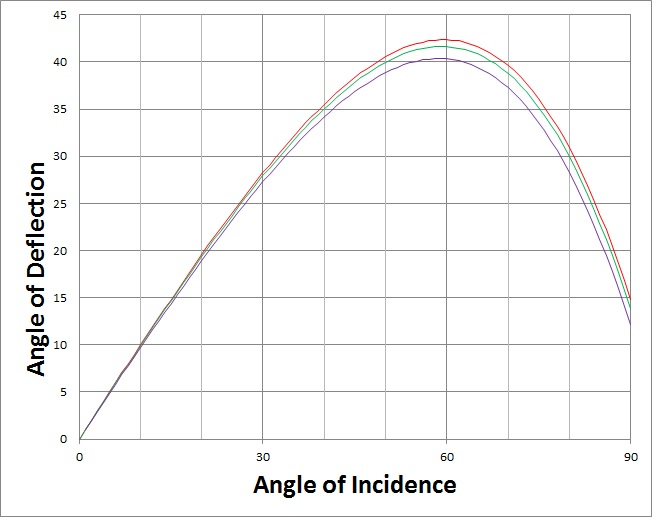
Clouds changing color inside rainbow arch
Again, the process known as "color separation" applies to individual rays of incoming light, not to the image as a whole. The green band contains lesser intensities of red, orange, and yellow light; but not blue, indigo, or violet. Citing "color separation" as the root cause of the rainbow does not explain this. Citing "color aberration" does. But by citing "color separation," it is easy to come to the conclusion that each color band comprises just one frequency of light (with allowances for the 0.5° width of the sun). And if you search the internet for explanations of the rainbow, you will find this incorrect conclusion explicitly mentioned in a many, maybe even a majority, of them. All I'm trying to do is separate (pun intended) the process as it applies to individual rays from the process that causes the rainbow. This misconception is furthered when people incorrectly call Newton's "colors of the spectrum" the "colors of the rainbow." They are not the same; my second figure above shows this. This explanation is not symmetric in regard to different colors; I'm not sure why you claim that, or how you got those orders. The maximum angle of the deflection depends on the index of refraction, and I illustrated this in my first figure. I admit that I was trying to be brief, and so left the asymmetry to the interpretation of that figure, but it is there. The maximum for red light is about 42°, so the red band is seen reflected from drops that are about 42° from the sub-solar point (the shadow of your head). This is the outside, not the inside, of the rainbow. The maximum for green light is about 41°, so the green band is seen reflected from drops that are about 41° from the sub-solar point. This is the middle of the rainbow. The maximum for violet light is about 40°, so the violet band is seen reflected from drops that are about 40° from the sub-solar point. This is the inside, not the outside, of the rainbow. Maybe this will help: The maximum of intensity is caused because the functional relationship between the incident angle and the deflection angle has a maximum around i=60° and d=40° to 42°. And the intensity of the light is inversely proportional to the slope of this function. The intensity is illustrated by how the light rays "bunch up" near the maximum. This is exaggerated: Yes, each colors separate in individual incoming rays. But not as that implies in the full set of outgoing rays. +++++ [Edit] Swansont wrote: There is no difference, except how the colors are formed. If we could create an array of small prisms suspended in the air, and all aligned the same way, we would see a linear band of spectrum (i.e., not quite the same as rainbow) colors across the array. The image project from one is the same as the image seen in the array. Then say we have a screen, with a hole cut in it so that we can shine a bright beam of white light through it. Place a spherical flask of water in the beam. It will reflect a white circle of light onto the screen, with rainbow (i.e., not quite the same as spectrum) colors around the rim. Something like this: The point is that the reflection from one, and the image from an (aligned) array, are the same.
-
Prove the negative of the Monty Hall problem
Those who intuit that the answer is 50:50 are using what is known as the Principle of Indifference on the two closed doors. And it doesn't apply to them. But they shouldn't be criticized too much - the reasons for why it doesn't apply have nothing to do with mathematics, and many who should know better get it wrong in other problems. If the paths needed to reach two different outcomes are identical, except for the names we apply to the details, then the PoI says that they should have the same probability. That is, if we have no reason to claim one result is more, or less, likely, then we must consider them to be equally likely. If a process has N different outcomes that all have this property, then each has probability 1/N. This principle is so ubiquitous that we may not realize we are applying it. It is why we say that the car has a 1/3 chance to start behind each of the three doors. To our knowledge, there is no reason why there is more, or less, reason for the car to be behind door #1, #2, or #3. Let's say that the contestant originally picked door #1, and the host opened door #3. These are just the names that make no difference to the PoI, and using names makes it easier for me to talk about the solutions. Then: To say the answer is 50:50, you first have to say that you know of nothing that distinguishes door #1 from door #2. This is definitely not true: it was possible for door #2 to have been opened, but impossible for door #1 since the host would never open the contestant's door. Once you have identified a difference, you have to have a reason to suspect that this difference affects the probability of reaching the known result, that door #3 was opened. If the car is behind door #2, a 1/3 chance, then the host was forced to open door #3. If the car is behind door #1, then the host had a choice. Either door #2 or door #3 could have been opened. The PoI no longer applies, and the answer cannot be 50:50. The PoI does apply to which door the host chooses to open when the car is behind door #1. With two choices, the probability of door #3 being opened is halk of what it was before this information. This makes the probability that the car is behind #2 (the first case in this list) twice that of #1. The answer is 1/3:2/3 The reason this is hard to see, is that it was not made clear that we know which door was opened. +++++ It is the way that the MHP problem is presented that makes it seem self-evident that door #1 and door #2 are equivalent, when they are not. There are other problems where the exact same reasoning should apply, but the presentation isn't the same. Mr. Smith has two children. At least one of them is a boy. What is the probability that both children are boys? The most naive solution here is that "the other" child - the one who may or may not be a boy - must have a 50% chance to be a boy. This is wrong because no specific child was identified as "the boy." That is, if there are two boys, which is "the other"? (This might be easier to see if the family had five children, with at least two boys. Which are "the other three"?) So the error is in determining the set of cases, not applying probability theory to them. Many experts will explain that in a two-child family, there are three equally-likely (by an idealistic application of the PoI) combinations. Based on birth order, those that that fit the given information are: BB, BG, and GB. If the PoI applies to them, each should have a 1/3 probability, and the answer is 1/3. But if you examine this logic, you can see that it is the same logic used to get 50:50 in the MHP. Only the number of possibilities has changed. The issue is whether the BB possibility is equivalent, under the PoI, to the BG and GB possibilities. Martin Gardner, who first posed this problem (1959 in his Scientific American column), originally answered "1/3." But he retracted that answer, claiming the question was ambiguous. Specifically, it did not distinguish between the many ways you could know that at least one child is a boy: You asked Mr. Smith "Do you have at least one boy?", and he said "yes." You met a son. Mr. Smith told a story about a son. Mr. Smith is a Boy Scout leader. etc. The PoI applies only to the first case. In almost any other reasonable way to learn "at least one is a boy," the PoI does not apply since you could also have learned that there was at least one girl. This has the same result as the host choosing between two doors, and it makes (as Gardner admitted) the answer 1/2.
-
Clouds changing color inside rainbow arch
Yes, the effect on any one incoming ray is the same as what you call "color separation." No, when seen as a whole, the effect on the resultant image is not due to that effect. Different colors from different parts of the original end up in the same place, not "separated" at all. And the reason I make this fine distinction is because many people believe, incorrectly, that the green band in a rainbow is completely "separated" from red. They believe that, because they attribute the rainbow to "color separation." And that is wrong. What happens in prisms, only happens when there is a single ray of incoming white light (or parallel rays that extend in the same direction as the axis of the prism, so that the paths from different incoming rays experience the exact same deflections). What happens is that each color is deflected to a different place than any other color. What happens in lenses and raindrops, where different rays do not experience the same deflections, is that the size of the resultant image varies by color.
-
Clouds changing color inside rainbow arch
I just joined, and wanted to get my post count up . So I looked for some of my pet topics in old posts, and I think this one needs a better response in a science forum. Most explanations of rainbows are satisfactory for middle schoolers, but get many details wrong if you go above that level of education. The problem is that it sounds so reasonable, that few students doubt the accuracy, and they repeat it when they become teachers. The short explanation is that spherical raindrops do not act like prisms, they act like lenses (or the mirror in the back of a flashlight). The colors are not caused by the literal act of color separation, it is a secondary effect called color aberration. And the bands are caused by ... well, it isn't a simple analogy. A spherical raindrop reflects light back toward the sun at every angle from 0° (straight back toward the sun) to about 40°. So the complete reflection is a beam of light, like from a wide-beam flashlight, that is about 80° wide. But the beam does not have a constant brightness. In increases slowly as the incident sunlight moves off-center. And it actually becomes asymptotic at the maximum reflection angle. See the first figure below. But the sun is actually about 0.5° wide, so this asymptote creates a bright band of light that is 0.5° wide. The effect of diffraction is not to separate colors, it is to change this maximum angle. It's about 40° for violet light, and about 42° for red light. So the bright bands for different colors are slightly offset, and the colors get less vivid as you move from red to violet. See the second figure (from https://atoptics.co.uk/bows.htm) Finally, the area in the sky that is inside the bright bands still has some reflected light. This makes the sky there appear brighter, but what is usually noticed is that the sky outside is darker. It has been named Alexander's Dark Band for the man who first wrote about it. Third figure. The same thing happens with the secondary bow. But the colors aren't "reversed," the bow is actually seen up-side down. Technically, the bright inside extends past the top of the sky and goes to the sun itself. You usually can't see this. Other answers did explain the pinkish hue correctly.
-
problem with cantor diagonal argument
Why do you think D1 and D2 appear in any list that is used as an "example of CDA"? Are you still under the impression that CDA starts with a statement like this? Assume you are "working with" a list of the complete set of infinite binary sequences. That impression is understandable, for one who has not actually read the paper where Cantor presented CDA. It is commonly claimed to be the first line. But you have read it; I know this, because I saw you quote it in a different post. The proposition he proves is (in literal form and an informal translation in the style you use for Ann and Bill) : If E1, E2, …, Ev, … is any simply infinite [einfach unendliche] series of elements of the manifold M, then there always exists an element E0 of M, which cannot be connected with any element Ev. If Ann "works with" an infinite list of infinite binary sequences, then there is always an infinite binary sequence a0 that is not in Ann's list. To prove this, Cantor starts out by saying: For proof, let there be E1 = (a1.1, a1.2, … , a1,v, …), E2 = (a2.1, a2.2, … , a2,v, …), Eu = (au.1, au.2, … , au,v, …), ... , where the characters au,v are either m or w. Sorry for the copy-and-paste text, I got it straight from Logicmuseum. For proof, let Ann start out with a list like 111001..., 000111..., 101100..., ... Now please, please notice that neither of the statements says "assume that every infinite binary sequence is listed." They just have to be lists that actually do exist. Cantor did make one mistake here - technically, he should prove (by example is sufficient) that at least one such list is possible. You didn't imply how Ann and Bill determine any more members. But here's one: 100000... 010000... 001000... ... So, let's go back to my question at the top. Why do you think D1 and D2 appear in any list? Yes, they should appear in any complete list, but what has that to do with Ann's and Bill's lists? The sequence a0 (that you call D1) does not appear in Ann's list. Whether or not it appears in Bill's is irrelevant - they afr not necessarily listing the same set of sequences. The sequence b0 (that you call D2) does not appear in Bill's list. Whether or not it appears in Ann's is also irrelevant. But we can follow this with the conclusion of CDA, which is actually the contradiction that you tried to use to claim it was invalid: It follows immediately that the totality of all elements of M cannot be put into the sequence [Reihenform]: E1, E2, …, Ev, … otherwise we would have the contradiction, that a thing [Ding] E0 would be both an element of M, but also not an element of M. It follows immediately that Ann (or Bill) could not have been "working with" a listing of all infinite binary sequences. Because that would mean that the string a0=D1 (or b0=D2) was both in the set listed by Ann (or Bill), but also not in that set. CDA actually isn't very hard to understand. It is unfortunate that it gets taught incorrectly, becasue that does get in the way of understanding it. But you can't disprove it by intentionally ignoring what it says, and using its contradiction against itself.