

Genady
-
Posts
5073 -
Joined
-
Days Won
51
Content Type
Profiles
Forums
Events
Posts posted by Genady
-
-
6 minutes ago, Maartenn100 said:
The neural correlates are just the outer appearance of this inner world, dimension, or space, seen from the viewpoint of another mind. The neural correlates are 'this inner space and inner thoughts' seen in the perceptions of another mind. The neural correlates of consciousness do not cause the mind, they are the mind, seen from the perspective of another mind.
Sorry, I guess it makes sense to you, but it doesn't make sense to me. Just words. Got a model?
0 -
9 minutes ago, DanMP said:
So the curvature has no cause?
Yes, it has not. Every spacetime has a curvature.
0 -
2 minutes ago, Maartenn100 said:
Science (as concept) is non-physical. Without this non-physical mind you could not read these words here on the page or any other book for that matter. Take the non-physical mind away from the world, and science ceases to exist.
Just replace "non-physical" with "physical" and "mind" with "brain":
Science (as concept) is physical. Without this physical brain you could not read these words here on the page or any other book for that matter. Take the physical brain away from the world, and science ceases to exist.
Yes.
0 -
6 minutes ago, DanMP said:
Time dilation is the "dominating effect" or the dominating [apparent] cause?
I wrote apparent because, in my opinion, the actual cause of gravity is the one that creates "the curvature" ...
Since energy-momentum and curvature are not timelike separated, there is no meaningful causal relation between them.
0 -
18 minutes ago, KJW said:
Why don't you try an infinitesimal translation to find out:
xμ⟶xμ+δxμ
Note that:
f⟶f+∂μf δxμ
I did, and my answer was that \(\mathcal L\) is invariant under translation.
0 -
42 minutes ago, Maartenn100 said:
I am asking here and now for immediate recognition from the physicalists for this non-physical dimension or space where thoughts, inner images, the inner voice, dreams, and experiences reside!
No.
0 -
The Lagrangian, \[\mathcal L(x)= \frac 1 2 \partial^{\mu} \phi (x) \partial_{\mu} \phi (x) - \frac 1 2 m^2 \phi (x)^2\] for a scalar field \(\phi (x)\) is said to be "Lorentz invariant and transforms covariantly under translation."
What does it mean that it transforms covariantly under translation?0 -
1 hour ago, wazzup said:
is there a calculation of the arc using the 2 dia sizes of the pellet
You also need the length of the pellet.
0 -
2 minutes ago, joigus said:
4000 ya
Isn't it rather 6000? 😄
1 -
2 minutes ago, cryptocracy said:
When the world first formed, its rotation speed was faster than it is now and it started to slow down. Will the slowdown be faster when the moon disappears?
6 minutes ago, Genady said:It will stop slowing down (almost).
42 minutes ago, cryptocracy said:I get it but I guess it's not just limited to tides
Another ecological effect will be on organisms which use Moon for timing, for example, coral spawning.
1 -
1 minute ago, cryptocracy said:
What will be the effect on the earth's rotation speed?
It will stop slowing down (almost).
1 -
12 hours ago, KJW said:
Gravitational time dilation is the change in the length in spacetime of a timelike worldline with respect to height and is geometrically related to the curvature of the worldline, which corresponds to the acceleration we experience standing on the ground on earth.
This ^^^^, I understand.
8 hours ago, KJW said:the analogy that enables someone to appreciate the esoteric nature of gravity in terms of the geometry of something as familiar as a slinky or a disc.
This ^^^^, is only a distraction to me.
(But generally, more often than not, I dislike analogies. Perhaps something individual.)
0 -
1 hour ago, KJW said:
The familiar gravity that we all experience on earth is caused by gravitational time dilation.
Yes, it is, in this sense:
"This is extremely general. In any kind of gravitational field, as long as it is more or less constant with time, and not doing anything too radically relativistic, the coefficient in front of \(dt^2\) in the metric is always one plus twice the gravitational potential."
Susskind, Cabannes. General Relativity: The Theoretical Minimum (p. 155).
0 -
2 hours ago, joigus said:
should be written as
I'm at ease with the Schwartz's notation by now. It is as simple as mentally substituting \(A_{\mu} g^{\mu \alpha} B_{\alpha}\) every time he writes \(A_{\mu} B_{\mu}\).
0 -
I'm looking where exactly, during a construction of the Feynman propagator \(D_F(x_1,x_2)\), a particle goes off-shell.
It is on-shell all the way until before the last step:
\(D_F(x_1,x_2)=\frac i {(2 \pi)^4}\int d^3 k \int d \omega \, e^{-i \vec k (\vec x_1 - \vec x_2)} \frac 1 {\omega^2 - \omega_k^2 + i \epsilon} e^{i \omega (t_1-t_2)}\)
The particle is on-shell here because its 4-momentum is \((\omega_k, \vec k) \), where \(\omega_k^2 = \vec k^2+m^2\).
Integration variable of the first integral is 3-momentum \(\vec k\), where each one of the three component varies from \(- \infty\) to \(\infty\).
Integration variable of the second integral is energy \(\omega\), which also varies from \(- \infty\) to \(\infty\).
Now, we combine these integration variables into a new 4-vector \(k=(\omega,\vec k)\), where each component varies independently from \(- \infty\) to \(\infty\). This 4-vector is not a 4-momentum of anything and thus is off-shell for a simple reason that there is no shell for it to be on. It is just an integration variable:
\(D_F(x_1,x_2)=\frac i {(2 \pi)^4}\int d^4 k \, e^{-i \vec k (\vec x_1 - \vec x_2)} \frac 1 {\omega^2 - \omega_k^2 + i \epsilon} e^{i \omega (t_1-t_2)} = \frac i {(2 \pi)^4}\int d^4 k \frac {e^{k (x_1 - x_2)}} {\omega^2 - \omega_k^2 + i \epsilon}\)
Being a generic 4-vector, \(k\) satisfies \(\omega^2=k^2+ \vec k^2\).
Being an on-shell 4-momentum, \((\omega_k, \vec k) \) satisfies \(\omega_k^2 = \vec k^2+m^2\).
Substituting these above, we get the final form of the Feynman propagator:
\(D_F(x_1,x_2)= \frac i {(2 \pi)^4}\int d^4 k \frac {e^{k (x_1 - x_2)}} {k^2 - m^2 + i \epsilon}\)
The particle, which is on-shell, is not explicit in this form. Instead, we have a generic variable \(k\), which is a Lorentz invariant way to package the four integration variables, and which is not a 4-momentum of any particle. Evidently, there are no off-shell particles here.
0 -
Unfortunately, I can't read this post:
1 hour ago, RobertSmart said:Given Lagrangian:
4L=−21ϕ□ϕ+21m2ϕ2−4!λϕ4
The Euler-Lagrange equation is:
∂ϕ∂L+□(∂(□ϕ)∂L)=0
and I don't know how his result is different from mine, but it seems that his EL equation is the same as mine,
On 2/27/2024 at 6:36 PM, Genady said:The EL equation:

<<<<<
which is different from
36 minutes ago, joigus said:we get as the only Euler-Lagrange equation,
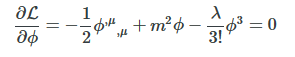
<<<<<<<
I disagree with the latter. We need to use the generalized EL equation, which I have already derived in this exercise:
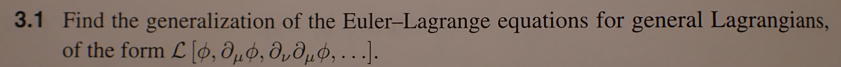
and got the answer compatible with this:
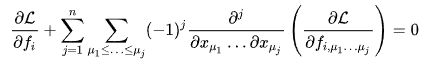
(Euler–Lagrange equation - Wikipedia)
1 -
Write down the next-order diagrams for the equation of motion \(\Box h - \lambda h^2 -J =0\). Check the answer using Green's function method.
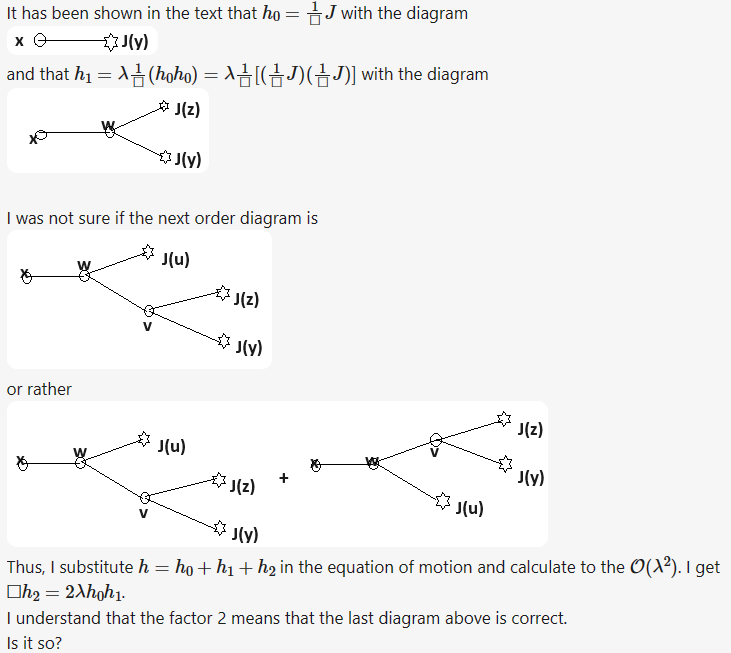 0
0 -
Q: How many constants \(c\) are there so that \(\phi(x)=c\) is a solution to the equation of motion?
A: Three. \(c=0\) and two solutions for \(c^2= \frac {3!} {\lambda} m^2\)
Q: Which solution has the lowest energy (the ground state)?
A: The potential energy from the Lagrangian is \[\frac {\lambda} {4!} \phi^4 - \frac 1 2 m^2 \phi^2\]It is the lowest for the non-zero \(c\): \(- \frac{3!m^4} {4 \lambda}\).
0 -
This is a multi-step exercise. It would be very helpful if somebody could check my step(s) as I go. @joigus, I'm sure it is a child play for you.
I'd like to make sure that I've derived correctly the equation of motion for this Lagrangian:
\[\mathcal L=- \frac 1 2 \phi \Box \phi + \frac 1 2 m^2 \phi^2 - \frac {\lambda} {4!} \phi^4\]
The EL equation:
\[\frac {\partial \mathcal L} {\partial \phi} + \Box \frac {\partial \mathcal L} {\partial (\Box \phi)} = 0\]
The equation of motion:
\[\Box \phi - \frac 1 2 m^2 + \frac {\lambda} {3!} \phi^3 = 0\]
How is it?
P.S. As edit LaTex does not work, I add a typo correction here. The equation of motion is rather
\[\Box \phi - m^2 \phi + \frac {\lambda} {3!} \phi^3 = 0\]
1 -
21 minutes ago, joigus said:
at this point in your life
The advantage is, no deadlines.
0 -
I think, I got it.
The symmetry validates the equation (3), because this equation makes the variation of Lagrangian a total derivative, and this makes the variation of action vanish:
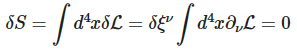
IOW, without the symmetry, we can't go from (4) to (5).
1 -
Rather than trying to fix the OP, I've prepared the text elsewhere and just post its image:

A minor correction: the equation (4) above should rather be
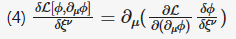 0
0 -
Here are steps of derivation of energy-momentum conservation:
Consider a shift of the field ϕ by a constant 4-vector ξ :
(1) ϕ(x)→ϕ(x+ξ)=ϕ(x)+ξν∂νϕ(x)+...
The infinitesimal transformation makes
(2) δϕδξν=∂νϕ
and
(3) δLδξν=∂νL
Using the E-L equations, the variation of Lagrangian is
(4) δL[ϕ,∂μϕ]∂ξν=∂μ(∂L∂(∂μϕ)δϕδξν)
Using (2) and (3),
(5) ∂νL=∂μ(∂L∂(∂μϕ)∂νϕ)
or equivalently
(6) ∂μ(∂L∂(∂μϕ)∂νϕ−gμνL)=0
The conclusion is, "The four symmetries have produced four Noether currents, one for each ν :
(7) Tμν=∂L∂(∂μϕ)∂νϕ−gμνL
all of which are conserved: ∂μTμν=0 ."
My question:
where in this derivation the assumption was used that the transformation is a symmetry?
P.S. I am sorry that LaTex is so buggy here. I don't have a willing power to do this again. Ignore. Bye.
0 -
test
in The Sandbox
\[\phi(x) \rightarrow \phi(x+\xi)=\phi(x)+\xi^{\nu} \partial_{\nu} \phi(x) + ...\]
\[\frac {\delta \phi} {\delta \xi^{nu}} = \partial_{\nu} \phi\]
\[\frac {\delta \mathcal L} {\delta \xi^{nu}} = \partial_{\nu} \mathcal L\]
\[\frac {\delta \mathcal L[\phi, \partial_{mu} \phi]} {\partial \xi^{\nu}}=\partial_{mu} (\frac {\partial \mathcal L}{\partial (\partial_{mu} \phi)} \frac {\delta \phi} {\delta \xi^{nu}})\]
0

What is gravity?
in Modern and Theoretical Physics
Posted
Not necessarily. For example, the Schwarzschild geometry exists in vacuum.