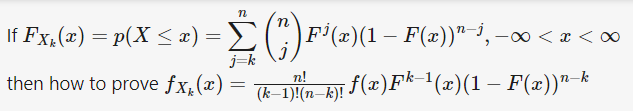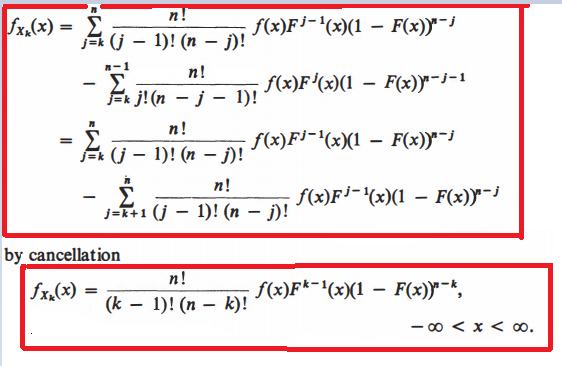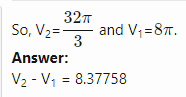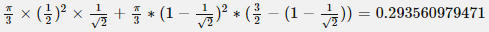Everything posted by Dhamnekar Win,odd
-
Using line integral to find the lateral surface area of some part of a cylinder
I got the answer to this question. I computed it as follows: [math]\displaystyle\int_0^{2\pi} 12 dt = 24\pi[/math]
-
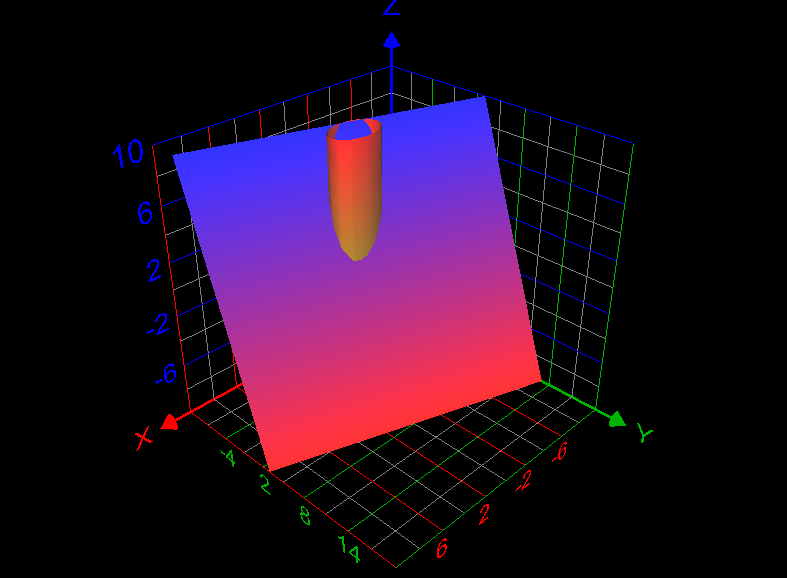
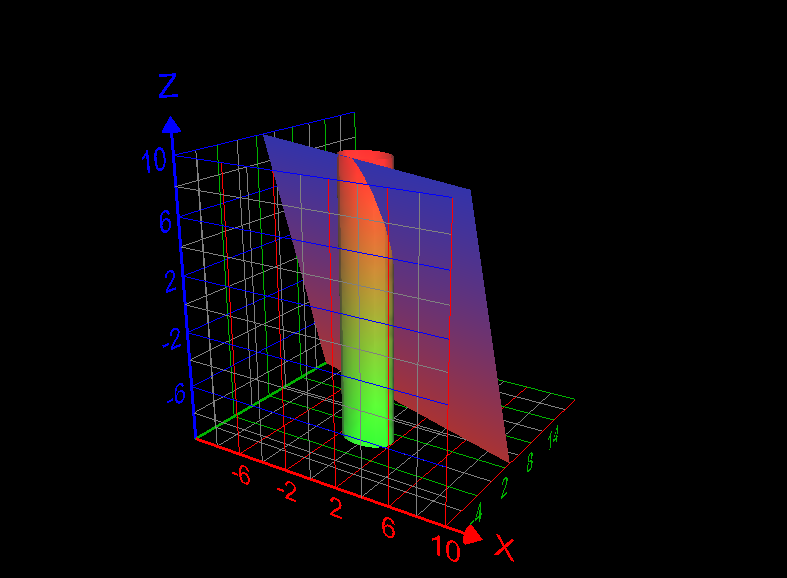
Using line integral to find the lateral surface area of some part of a cylinder
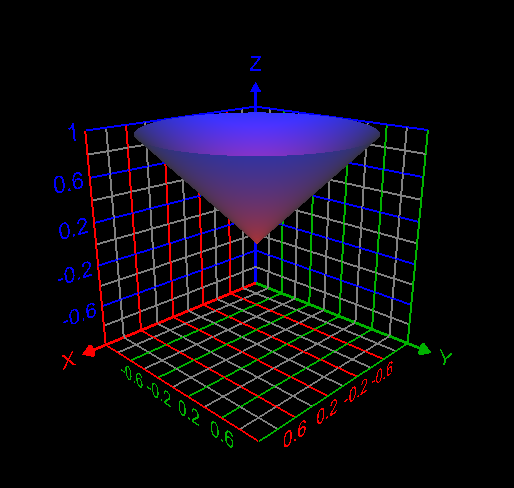
Use a line integral to find the lateral surface area of the part of the cylinder [math]x^2 +y^2 =4[/math] below the plane x + 2y + z =6 and above the xy-plane. How to answer this question? What is the answer of this question? Graph of the required lateral surface area of the cylinder is given below:
-
Derivation of P.D.F. from distribution function
I tag this question as 'SOLVED'. Author's computations are correct. Thank you.
-
Derivation of P.D.F. from distribution function
After studying these author's computations, I understood the differentiation part but I don't understand cancellation part and final term computation.
-
Derivation of P.D.F. from distribution function
Author computed [math]F_{X_k} (x)[/math] as follows. but I don't understand it. Would any member explain me the following computations?
-
Computing center of mass
- Computing center of mass
- Finding the volume of the solid using change of variables technique
- Finding the volume of the solid using change of variables technique
I think my answer in the original post is incorrect. So, I want to correct it. My corrected answer is [math] \displaystyle\int_0^{2\pi}\displaystyle\int_0^2\displaystyle\int_0^4 r dz dr d\theta =16\pi [/math] Is this answer correct?- Finding the volume of the solid using change of variables technique
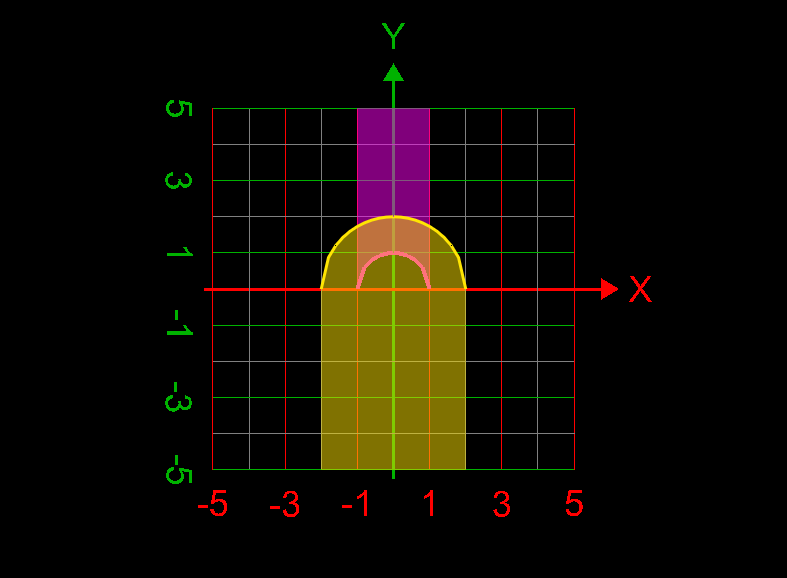
Find the volume of the solid bounded by [math]z = x^2 + y^2 [/math] and [math] z^2 = 4(x^2 + y^2) [/math] My attempt to answer this question: [math] \displaystyle\int_0^{2\pi}\displaystyle\int_0^2\displaystyle\int_0^4 1 \rho^2 \sin{(\phi)} d\rho d\phi d\theta = -\frac{128\pi \cos{(2)}- 128\pi}{3}= 189.822143919[/math] Is this answer correct?- How to use the change of variables technique here?
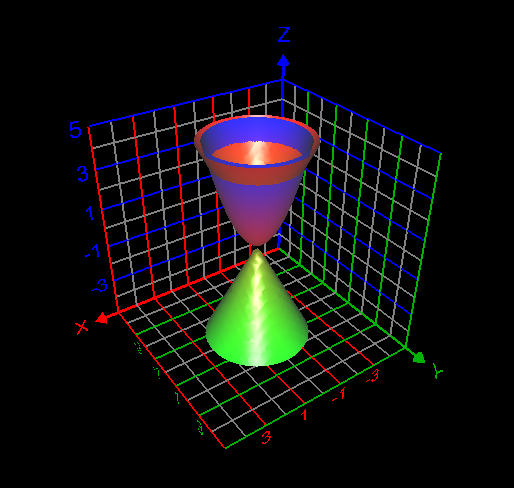
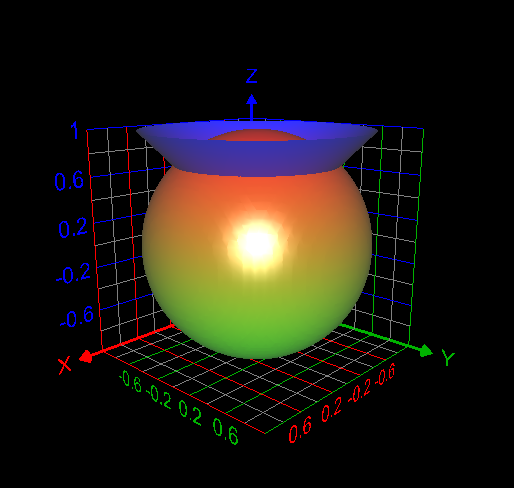
I computed the volume inside both the sphere [math] x^2 + y^2 + z^2 =1[/math] and cone [math] z= \sqrt{x^2 + y^2}[/math] as follows: [math]\displaystyle\int_0^{2\pi} \displaystyle\int_0^{\frac{\pi}{4}}\displaystyle\int_0^1 \rho^2 \sin{\phi}d\rho d\phi d\theta= 0.61343412301 =\frac{(2-\sqrt{2})\pi}{3}[/math]. This answer is correct.- How to use the change of variables technique here?
I want to correct the volume asked in the question computed by me = [math] \frac{\pi}{3} \times \frac12 \times \frac{1}{\sqrt{2}} + \frac{\pi}{3} \times (1-\frac{1}{\sqrt{2}})^2 \times (\frac{3}{\sqrt{2}} -(1-\frac{1}{\sqrt{2}}))=0.534497630798[/math]- How to use the change of variables technique here?
My attempt: I graphed the cone inside the sphere as in my first post. But I don't understand how to use the change of variables technique here to find the required volume. My answer without using integrals is volume of the cone + volume of the spherical cap = Is this answer correct? If correct, how to derive this answer using integration technique?- How to use the change of variables technique here?
Find the volume V inside both the sphere x2 + y2 + z2 = 1 and the cone z = [math]\sqrt{x^2+ y^2}[/math] How to use change of variables technique in this problem?- C program could not be executed at Windows command prompt
Yes. From that point of view, this program is wrong. But we already decided to ignore the leap year and we mentioned that as the comment.- C program could not be executed at Windows command prompt
- C program could not be executed at Windows command prompt
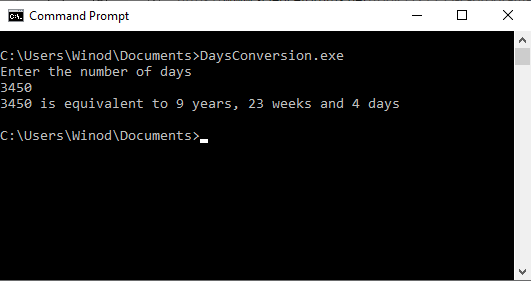
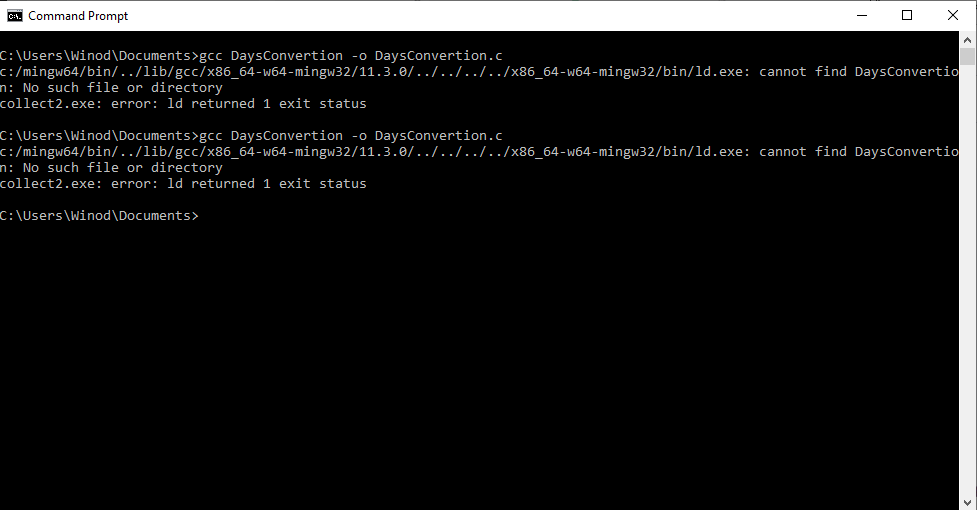
I have downloaded and installed ' C c-programs application from Windows store. I copied one program named 'Days Convertion' from it to my Notepad++ and saved it as c source file in the Documents folder. When I tried to compile it using gcc, gcc said unable to find the file. How can I fix this error? The c program is as follows: /* Write a c program to convert given number of days to a measure of time * given in years, weeks and days. For example 375 days is equal to 1 year * 1 week and 3 days (ignore leap year) */ #include stdio.h #define DAYSINWEEK 7 void main() { int ndays, year, week, days; printf("Enter the number of days\n"); scanf("%d",&ndays); year = ndays/365; week = (ndays % 365)/DAYSINWEEK; days = (ndays%365) % DAYSINWEEK; printf ("%d is equivalent to %d years, %d weeks and %d days\n", ndays, year, week, days); } /*----------------------------------------------- When I tried to compile it using gcc at windows command prompt, I got the following error several times. After giving this command at command prompt, 'DaysConvertion.c' file disappeared from the Documents folder. How can I fix this error?- How to debug the Java program that uses the Monte Carlo method to approximate the double integral?
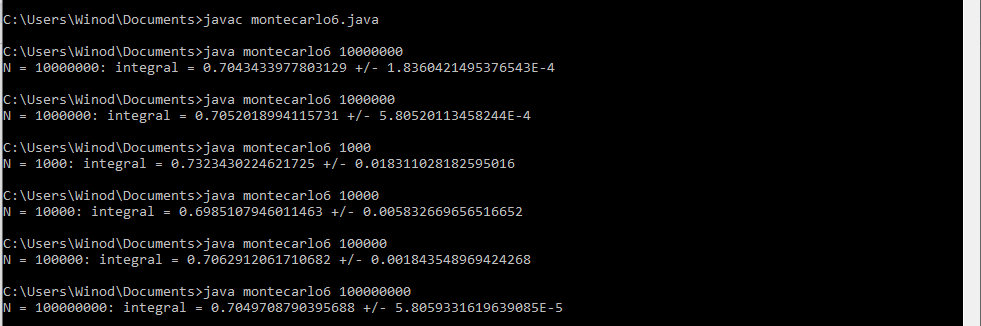
Yes. I think you are correct because as per your suggestion, I modified my Java program and I got the correct answer as given by author i-e 0.705. The modified java program and its new output is given below: //Program to approximate the double integral of f(x,y)=e^xy over the //region bounded by x=-1, x=1, y=0, and y=x^2 public class montecarlo6 { public static void main(String[] args) { //Get the number N of random points as a command-line parameter int N = Integer.parseInt(args[0]); double x = 0; //x-coordinate of a random point double y = 0; //y-coordinate of a random point double f = 0.0; //Value of f at a random point double mf = 0.0; //Mean of the values of f double mf2 = 0.0; //Mean of the values of f^2 for (int i=0;i<N;i++) { //Get the random coordinates x = 1 * Math.random() ; //x is between 1 and 0 y = 1 * Math.random() ; //y is between 0 and 1 if (y < Math.pow(x,2)) { //the point is in the region f = Math.exp(x*y); // Value of the function mf = mf + f; //Add to the sum of the f values mf2 = mf2 + f*f; //Add to the sum of the f^2 values } x = -1 * Math.random() ; //x is between -1 and 0 y = Math.random() ; //y is between 0 and 1 if (y < Math.pow(x,2)) { //the point is in the region f = Math.exp(x*y); // Value of the function mf = mf + f; //Add to the sum of the f values mf2 = mf2 + f*f; //Add to the sum of the f^2 values } } mf = mf/N; //Compute the mean of the f values mf2 = mf2/N; //Compute the mean of the f^2 values System.out.println("N = " + N + ": integral = " + vol()*mf + " +/- " + vol()*Math.sqrt((mf2 - Math.pow(mf,2))/N)); } //The volume of the rectangle [-1,1]x[0,1] public static double vol() { return 1*1; } } The new program's output:- How to debug the Java program that uses the Monte Carlo method to approximate the double integral?
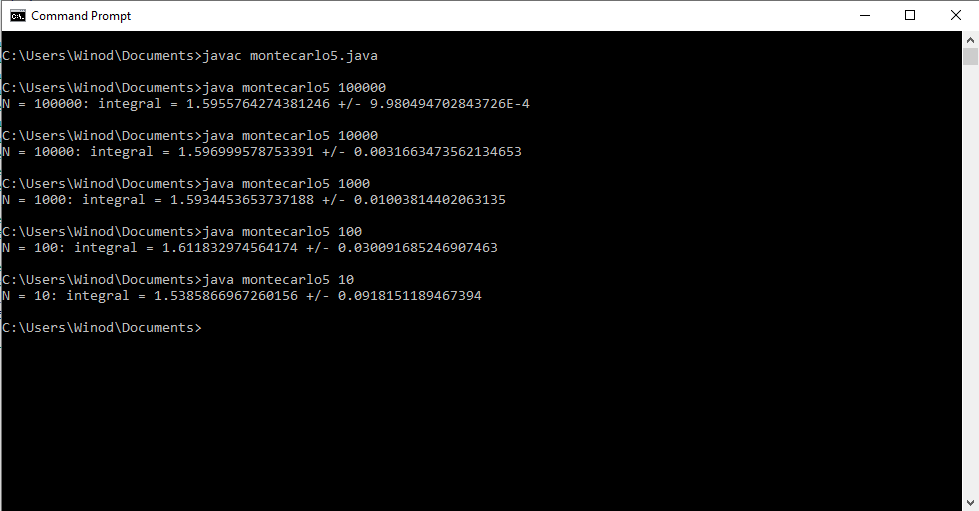
Write a program that uses the Monte Carlo method to approximate the double integral [math] \displaystyle\iint\limits_R e^{xy}dA [/math] where [math] R= [-1,1] \times [0, x^2][/math]. Show the program output for N = 10, 100, 1000, 10000, 100000 and 1000000 random points. My attempt: //Program to approximate the double integral of f(x,y)=e^xy over the //region bounded by x=-1, x=1, y=0, and y=x^2 public class montecarlo5 { public static void main(String[] args) { //Get the number N of random points as a command-line parameter int N = Integer.parseInt(args[0]); double x = 0; //x-coordinate of a random point double y = 0; //y-coordinate of a random point double f = 0.0; //Value of f at a random point double mf = 0.0; //Mean of the values of f double mf2 = 0.0; //Mean of the values of f^2 for (int i=0;i<N;i++) { //Get the random coordinates x = Math.random() ; //x is between 0 and 1 x = -1 * Math.random() ; //x is between -1 and 0 y = Math.random(); //y is between 0 and 1 f = Math.exp(x*y); // Value of the function mf = mf + f; //Add to the sum of the f values mf2 = mf2 + f*f; //Add to the sum of the f^2 values } mf = mf/N; //Compute the mean of the f values mf2 = mf2/N; //Compute the mean of the f^2 values System.out.println("N = " + N + ": integral = " + vol()*mf + " +/- " + vol()*Math.sqrt((mf2 - Math.pow(mf,2))/N)); } //The volume of the rectangle [-1,1]x[0,1] public static double vol() { return 2*1; } } Program Output is as follows: Correct integral =0.705; My Java program showed a integral 1.596 which is wrong, so my program is also wrong. How do I debug this program?- Maximization using Lagrange Multipliers
- Maximization using Lagrange Multipliers
- Normality computations
Are these above normality computations correct? If yes how? I don't understand these computations. Any chemistry help will be accepted.- Computations of a cell or solution potentials
Answer to question(d): Co3+ + V2+ → Co2+ + V3+ Defined redox couple is Co3+/Co2+ system [math] [Co^{2+}] = \frac{0.0050 mol}{0.200L} =0.025 M, [Co^{3+}]= \frac{0.010 mol}{0.200 L}=0.050 M, E_{sol}= E^{\circ}_{Co} -\frac{0.059}{n} \log{\frac{[Co^{2+}]}{[Co^{3+}]}} = 1.82 V - \frac{0.059}{1}\log{\frac{[0.025]}{[0.050]}} =1.84 V [/math]- Computations of a cell or solution potentials
If I write the balanced equation as 2VO2+ + Zn0 + 2H+ ⇌ 2VO2+ + Zn2+O-2 + H2O Is this correct?- Computations of a cell or solution potentials
Hi, Thanks for finding out the fault in my answer. Now, I rewrite the corrected balanced reaction 2VO2+ + Zn0 + 4H+ ⇌ 2VO2+ + Zn2+ + 2H2O - Computing center of mass
Important Information
We have placed cookies on your device to help make this website better. You can adjust your cookie settings, otherwise we'll assume you're okay to continue.
Account
Navigation
Search
Configure browser push notifications
Chrome (Android)
- Tap the lock icon next to the address bar.
- Tap Permissions → Notifications.
- Adjust your preference.
Chrome (Desktop)
- Click the padlock icon in the address bar.
- Select Site settings.
- Find Notifications and adjust your preference.
Safari (iOS 16.4+)
- Ensure the site is installed via Add to Home Screen.
- Open Settings App → Notifications.
- Find your app name and adjust your preference.
Safari (macOS)
- Go to Safari → Preferences.
- Click the Websites tab.
- Select Notifications in the sidebar.
- Find this website and adjust your preference.
Edge (Android)
- Tap the lock icon next to the address bar.
- Tap Permissions.
- Find Notifications and adjust your preference.
Edge (Desktop)
- Click the padlock icon in the address bar.
- Click Permissions for this site.
- Find Notifications and adjust your preference.
Firefox (Android)
- Go to Settings → Site permissions.
- Tap Notifications.
- Find this site in the list and adjust your preference.
Firefox (Desktop)
- Open Firefox Settings.
- Search for Notifications.
- Find this site in the list and adjust your preference.