-
Posts
14 -
Joined
-
Last visited
Content Type
Profiles
Forums
Events
Everything posted by Kino
-
What's the metric of your wormhole? If you don't know that then the answer is "not enough information".
-
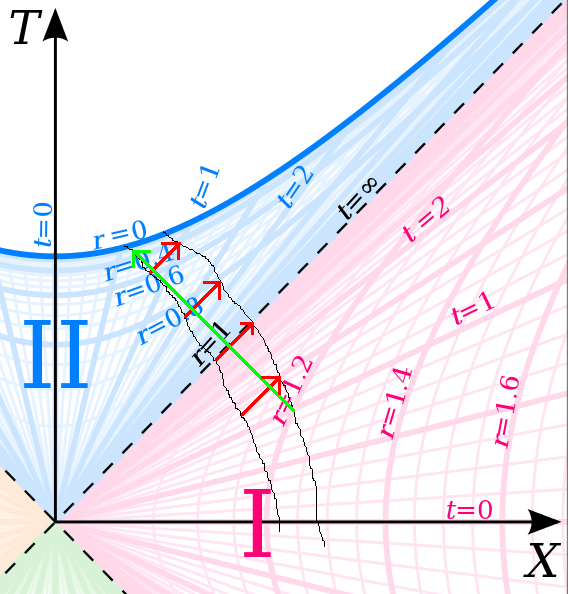
One of the easier visualisations is, IMO, a Kruskal diagram. Null paths in it are 45 degree lines, and the event horizon is one such. The axes of local inertial frames are (very small) x shapes, squished towards one or other of the light cone arms. If this sounds a bit like a Minkowski diagram, it should. But here the representation of spacetime is very distorted, so you can't extend those local axes infinitely as you can in Minkowski spacetime. And there's a lot of additional structure (a second exterior region and a white hole) that are artefacts of taking the Schwarzschild solution a bit too seriously. Here's a Kruskal diagram, copied from Wikipedia, with toe and head worldlines drawn (badly hand-drawn black lines), and a few light signals exchanged (red from toe to head, green from head to toe). I've only sketched the infaller's paths (badly), not calculated them. And they're quite a long way apart, so there isn't time for a light signal from the head to reach the toes inside the horizon. This would be possible if the lines were closer together. The reason I like this diagram is the simplicity of the light cones. It's easy to see what happens as someone falls in. You will see (receive a light signal from the event that) your toes cross the horizon as your head crosses. There is no invariant sense in which you can say that "your toes have now crossed" until your head also crosses, so you cannot report this. In your local inertial frame your toes do cross first, and you are free to report that your toes have now crossed (but others are free to disagree). Light signals can be exchanged both ways at all times (as long as both your head and toes cross), so you can never not see your toes.
-
He doesn't even seem to pay attention to his own posts, let alone anyone else's. See my comment about him proving that \(u.v> c^2\) for distinct \(u\), \(v\) then asserting that \(v.x=c^2\), with \(x\neq v\), implies \(x\) is a four velocity.
-
Correcting myself here: \(m\) can be anything it likes because it does exactly nothing. However if you insist that \(k^2\bar c^2=c^2\), then noting that \(\bar c^2\) is negative since \(a\) is spacelike, then \(k\) is imaginary.
-
Um... what?! You already showed on another thread that for two four velocities \(u\) and \(v\) their inner product satisfies \(u.v\geq c^2\), with equality iff \(u=v\). So what you should expect from (15) is that \(v-ka\) is not a four velocity, except in the case that \(ka=0\). In fact, a moment's thought would tell you that \(v-ka\) isn't even necessarily timelike. Furthermore, you already know that \(a\) is spacelike, so your \(m\) must be imaginary and cannot be 1 as you so blithely assert. This whole line of argument is utterly incoherent. If you want to see the effect of four acceleration on a four velocity you need to calculate \(a(\tau)\) or some other parameter, then integrate \(v(\tau)=v(0)+\int_0^\tau a(\tau')d\tau'\) (or whatever parameter you prefer to \(\tau\)). Simply adding a multiple of the four acceleration and hoping does not work.
-
I think the point (and what the OP proved) is that zero is consistent with the symmetries of the Riemann, naturally so because zero is the Riemann tensor of flat spacetime. But it isn't the only tensor that satisfies those symmetries.
-
Since that is merely a disguised form of your (4), all you are saying is that a tensor that is antisymmetric is antisymmetric. Taking six equations to get to a tautology seems excessive, but isn't wrong. (7) still does not follow from (6). I already gave an example of a non-zero Riemann tensor that satisfies (6). All you've done is shown that a zero tensor is not inconsistent with some of the properties of the Riemann. I have no idea which comment you are referring to.
-
In this thread, I think the problem is that OP did not realise that using the label \( R_{\alpha\beta\gamma\delta} \) for a tensor does not make it the Riemann tensor (a zero tensor satisfies the constraint placed on the tensor here but not all constraints on the actual Riemann). In the "Enigma of the tensors" thread I think it is incorrect index gymnastics. In "Norm Square of the Four Acceleration Vector" it is a misunderstanding of calculus. In "On Four Velocity and Four Momentum" it is that two vectors with a specified norm will not add to another vector with the same norm. I do not think OP has just one single problem.
-
It's worse than that. (4') has two free indices on the left and either zero or one on the right depending on how you interpret the repeated \( \mu \). And look at the indices in the first equation in the un-numbered block after (4''). Indices \( \rho \) and \( \sigma \) are used on the unbarred tensor and the barred coordinate differentials. Compare with the correctly stated transformation, (1). So the two derivatives not in brackets are (probably...) the barred-to-unbarred transform applied to the already unbarred tensor. Then we get to your point about whatever it is OP thinks they are doing with the triply repeated \( \alpha \). Having looked at a few more of the OP's postings I think they believe that there is something fundamentally wrong with maths. Therefore they expect illogical and contradictory results and, when they get them, do not bother to check for their own errors.
-
This expression is clearly invalid because the indices do not match. This expression is clearly invalid because the indices do not match. Is \( \alpha \) a dummy index? Is \( \mu \) a dummy index? Obviously not true, and counterexamples are common. See, for example, Eddington-Finkelstein coordinates (non-diagonal) and Schwarzschild coordinates (diagonal) on Schwarzschild spacetime.
-
Thanks. It looks like you get an hour to edit, so it's not a big problem.
-
(7) does not follow from (6). The term in square brackets in (6) is symmetric in \( \alpha \) and \( \beta \), so (6) is satisfied by any arbitrary four-index tensor \( R_{\alpha\beta\gamma\delta} \) (not just the Riemann tensor) as long as it is antisymmetric in \( \alpha \) and \( \beta \). This is not surprising, since (6) is nothing more than a restatement of (4), which itself is nothing more than a statement that \( R \) is antisymmetric in its first two indices (true of the Riemann, but also of a great many other tensors). It certainly does not follow that all components of the Riemann tensor (or any other arbitrary four index tensor antisymmetric in its first two indices) are zero, as can be verified by (for example) calculating the Riemann tensor for the Schwarzschild metric and confirming that (6) is satisfied for at least one choice of \( \gamma \) and \( \delta \) for which at least some of the \( R_{\alpha\beta\gamma\delta} \) are non-zero. E.g: pick \( \gamma=r, \delta=t \). The non-zero \( R_{\alpha\beta r t} \) in (+---) signature Schwarzschild coordinates are \( R_{trrt}=2m/r^3 \) and \(R_{rtrt}=-2m/r^3 \). Thus (6) expands to \[ R_{trrt}(g^{t\mu}g^{r\nu}+g^{r\mu}g^{t\nu})+R_{rtrt}(g^{r\mu}g^{t\nu}+g^{t\mu}g^{r\nu})=\frac{2m}{r^3}(g^{t\mu}g^{r\nu}+g^{r\mu}g^{t\nu}-g^{r\mu}g^{t\nu}-g^{t\mu}g^{r\nu}) \]The term in brackets on the right hand side is clearly zero, so (6) is satisfied even though the Riemann tensor is clearly not zero.
-
Thanks! I think the easiest way to make the point is actually to extend your one liner. \( c^2=\eta_{\mu\nu}U^\mu U^\nu \) by definition, and hence differentiating with respect to \( \tau \) we get \( 0=\eta_{\mu\nu}A^\mu U^\nu+\eta_{\mu\nu}U^\mu A^\nu=2\eta_{\mu\nu}U^\mu A^\nu \). This equation is obviously satisfied if \( A \) is a zero vector. If it's not a zero vector, we simply note that for any \( U \) there exists a frame in which it represents a state of rest, and hence in that frame the only non-zero component is \( U^t=c \). In that frame \( 0=\eta_{\mu\nu}U^\mu A^\nu \) simplifies to \( A^t=0 \), but the spacelike components of \( A \) are not restricted. Thus in this frame \( \eta_{\mu\nu}A^\mu A^\nu=-((A^x)^2+(A^y)^2+(A^z)^2) \) is obviously negative, or zero iff the vector is a zero vector and, since the left hand side is manifestly covariant, it's negative in any coordinate system. I think this is everything useful that @Anamitra Palit expressed in equations 1-11 and the un-numbered equation immediately afterwards, just derived with much less mess. But you can differentiate \( 0=\eta_{\mu\nu}U^\mu A^\nu \) with respect to \( \tau \) again, giving \( 0=\eta_{\mu\nu}(A^\mu A^\nu+U^\mu J^\nu) \), where \( J^\nu=dA^\nu/d\tau=d^3t/d\tau^3 \) is the "four jerk". In the frame where \( U \) represents "at rest", this simplifies to \( cJ^t=\eta_{\mu\nu}A^\mu A^\nu \), which is manifestly non-zero if the four-acceleration is non-zero. So the OP is simply wrong when they state in the un-numbered equation before (12) than \( \gamma = \mathrm{const} \). That would only follow from \( d^2t/d\tau^2=0 \) if that were true for all \( \tau \) (which it isn't in general) or if \( d^nt/d\tau^n=0 \) for all \( n\geq 2\) (which isn't true in general). I see what you mean. The ones where I can see the maths all seem to have an error, too. By the way, is there any way to make LaTeX render in the preview? I still see the source, although it seems to render when posted.
-
Hasn't the OP just proved (in a rather long-winded way) that the inner product of four acceleration and four velocity is zero and, hence, that if the four velocity is \( V^t=c \), \( V^x=V^y=V^z=0 \) then the four acceleration has \( A^t=0 \) (and that the four acceleration is spacelike if it isn't zero)? They just appear not to have noticed that in general \( \frac{dA^t}{d\tau} \neq 0 \), so the conclusion that \( \gamma=\mathrm{const} \) does not follow. The fact that a function is instantaneously zero does not mean that either its integral or its derivative need be zero. To me, the argument looks similar to saying that in circular motion in the x,y plane there comes a point where \( (v_x,v_y)=(v,0) \), and at that point \( a_x=0 \), and hence \( v_x \) can never change and circular motion is impossible. Obviously that's nonsense, and realising that \( \frac{da_x}{dt}\neq 0 \) is a part of understanding why it's nonsense.