quiet

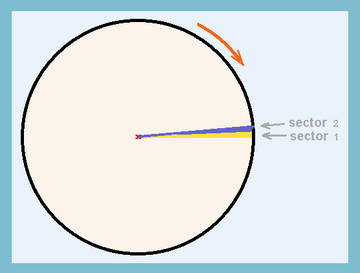
Let's go slowly. Let's look at the vector expression of Loretz's force. [math]F_{_L}= q \left( \vec{E} + \vec{v} \times \vec{B} \right)[/math] You know that the vector product is equal to zero when the vectors are parallel. And it is maximum when they are perpendicular. You only use a magnet. So the first term inside the parenthesis does not exist and remains [math]F_{_L}= q \ \vec{v} \times \vec{B}[/math] This means that the direction of wire movement can not be parallel to the direction of the magnetic field. The best condition is that they are perpendicular directions. --------- Outside of what was previously commented, what remains is conceptual understanding. In this phenomenon, the relative movement between the charge and the lines of the magnetic field is of interest. It is true that the description of the electromagnetic field devised by Faraday, in terms of field lines, is now considered obsolete. But for the concept that interests us I can not find a better description. From the questions you have answered, I understand that you have set up the experiment in the following way. 1. It is a magnet is a disk, with the poles on the sides of the disk. 2. The disk has uniform magnetization. Or at least, although it varies radially, it does not vary with the angular coordinate. 3. There is no relative movement between the disc axis and the 2 cm wire. The disk rotates but the axis remains fixed with respect to the wire. --------- With such an assembly, the wire sees no relative movement between itself and the magnetic field lines, regardless of whether the disk is rotating or still. Why ? Think of two contiguous circular sectors 1 and 2. When the disk rotates, the place that sector 1 leaves is occupied by sector 2. Both sectors are magnetically identical. Then the rotation of the disk does not cause a rearrangement of the lines of force of the magnetic field. The lines remain invariant, regardless of having the disk still, or spinning rapidly. The wire is still relative to the axis of the disk. Then it see invariant magnetic field lines, which remain motionless with respect to that wire. For that reason there is no potential difference between the ends of the wire, regardless of the angular velocity of the disk. --------- If you want to deepen the topic, you can ask the following. What would happen if instead of the oscilloscope you had an exquisitely sensitive instrument capable of measuring signals of atomic frequencies? In that case, when the disk rotates, the place left by an atom, an ion, a proton, an electron, can be occupied by a particle that is not magnetically identical to the previous one. Your esquisite instrument would react to the rearrangement of lines at the atomic scale and detect an irregular signal that, developed in a Fourier series, would have a fundamental component of atomic frequency. In other words, the spectrum of the signal would begin in that frequency order. --------- I hope I have understood the assembly well, otherwise the writing in this note is not valid.

Is the 2 cm wire placed at static position respect to the magnet?

Is disk magnetized? If it is, another question. Is a face of the disk one manetic pole and the other face the opposed pole?

Have you tried another wire length? If thre is no error in your experimemt, then the case is very interesting.

Thank you very much.

Hi icester. I will run the risk of asking a question without knowing your preparation in physics. Have you studied, mathematically or conceptually, the properties of electromagnetic induction? If you have not studied them, we can talk a bit about it.

I would like the written communication to convey how much I appreciate the gravitation chapter of that book. With an outstanding didactic quality, with beautiful and elegant style, it exposes the tools that allow to pose very diverse situations and access to specific bibliography. I have saved the images. It does not appear the author's reference in the sheets. I would like to know the data, if possible. I must confess that regarding gravitational interaction and other interactions, little by little a very different conviction has been installed in me than what appears in the bibliography. So different that seem to me it's an abuse to think about a gravitational field and apply the same kind of mathematical treatment that we use for the electromagnetic field. The issue exceeds the context of this thread. That is why I will not continue the comment.

It is true what you point out. The thread would have been better warning in the beginning that the model corresponds to incompressible material. Before your question, I had not noticed that detail. That's why I did not mention it in the beginning. I appreciate your intervention. Thanks also for the link. I have not followed the mathematical development. I have only read the concepts that I can, in some way, understand. It seemed to me that the objective of the advanced model shown in this publication is to explain, first, how the astronomical objects of the analyzed class are formed, to study later the evolution towards a condition with more or less stable averages in the magnitudes that describe the state. As I said, that seemed to me. Maybe you can confirm or correct my interpretation.

Thanks studiot for the question, which serves to reflect. We know that the density of a gas, approximately, increases with pressure, as long as the volume does not approach the value of the co-volume. Assuming constant density implies supposing that it is not a gaseous sphere. The constituent substance of the sphere is incompressible. In reality it seems difficult to find something that is strictly incompressible, maintaining that property in all conditions. In an ideal model, like this one that we have here, we can suppose perfect incompressibility in all conditions of pressure and temperature. And the model reports that ideal conditions do not prevent the existence of a critical region. The Chinese philosopher Confucius inverted the phrase, because he said that true understanding is given by the pair of symmetrical phrases that you get with the original phrase plus the inverted phrase. In your case we would have the next pair. For the same reason that cows are spherical For the same cows that reason is spherical

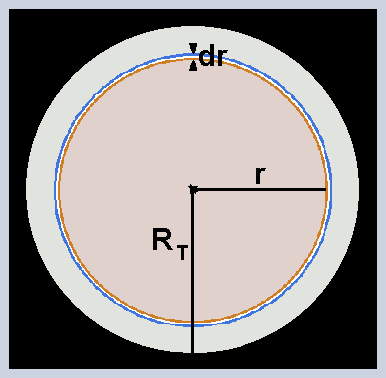
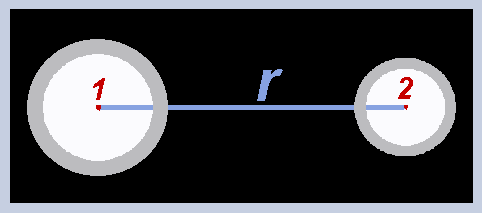
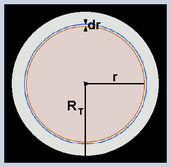
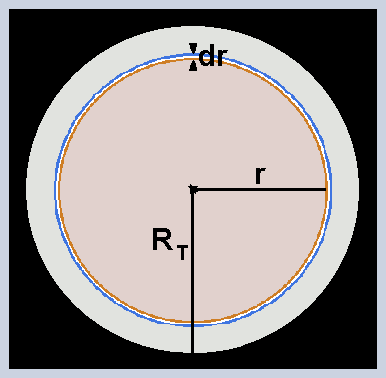
This thread is simply an application of Newton's gravitational law and of the two corresponding shell theorems. Why have I decided to place the subject in Speculations? Because in this section, if a debate is initiated, there is more freedom to expose opinions. In physics we can take the laws and theorems individually. In that way we obtain pieces of information, comparable with the pieces of a puzzle. Sometimes a problem requires applying laws and / or theorems jointly. This minimizes the amount of free parameters and, for that reason, reveals details that do not appear in individual applications, or in cases that are resolved by applying a less numerous set of laws and / or theorems. Regarding gravitation, Newton left a law of force and two theorems, called shell theorems. The law of force does not need comment. Let's go to the shell theorems. - Theorem 1 Shell material perfectly spherical. The density may be uniform, or it may be a function of the radius with spherical symmetry. In both cases the same theorem is viritated, which establishes the following. Let's abbreviate the word shell with the letter C. The gravitational force between C and an object located outside of C, has the same value that we would obtain supposing that all the mass of C is accumulated in the center of C. Example. To calculate the force between two shells of the type mentioned, the distance in the denominator of the force formula is equal to the distance between the centers of the shells. That is to say [math] F= G \ \dfrac{ m_{_1} \ m_{_2} }{r^2}[/math] - Theorem 2 The net gravitational force, exerted on a point object located inside the spherical shell, is equal to zero. It is fulfilled regardless of the location of the inner object. - Let's start now the topic that interests us. * Sphere with uniform density. * Validity of Newton's gravitational equation and the shell theorems within the body of the sphere. * All variables are continuous. That is, we can derive and integrate. Why uniform density? Think of a sphere made of foam rubber with uniform density. To alter that and achieve non-uniform density, work is needed. Then, with non-uniform density, the sphere has more energy than with uniform density. When conditions permit, the sphere will minimize its energy by releasing the excess, that is, it will return to the condition of uniformity. The law of force and Newton's shell theorems admit some density distributions in the sphere and others do not. Uniform density is a supported condition. Think of a spherical shell of infinitesimal thickness, defined within the sphere. That shell has an infinitesimal volume dV, expressed in the following way. [math]dV = 4 \ \pi \ r^2 \ dr \ \ \ \ \ \ \ \ \ (01)[/math] [math]r \ \rightarrow[/math] radius of the infinitesimal shell Symbolize P to a point on that shell. We want to calculate the gravitational force at that point. Theorem 2 informs that the part of the sphere located between [math]r[/math] and [math]R_{_T}[/math] exerts a net force equal to zero over P. Then only the part between the center and [math]r[/math] . Theorem 1 informs that we can assume accumulated in the center all the mass of the part that interests. This applies to all points of the infinitesimal shell. For that reason we can refer the calculation to the mass [math]dm[/math] of the whole infinitesimal shell. In that case, Newton's formula expresses the sum of all the modules. Which modules? There are infinite points, [math]P_{_1}[/math],[math]P_{_2}[/math],[math]P_{_3}[/math]...[math]P_{_n}[/math], all in the same condition as P. Although the force vectors of all those points have different directions, all the modules are equal. If we put in Newton's formula the mass [math]dm[/math] of the whole shell, the result is the summation of all the modules. The individual module at a point is equal to that summation, divided by the area of the spherical surface of radius [math]r[/math] and multiplied by the infinitesimal area corresponding to the point. If we started from the individual point, we would need to do an integral, to get the same result that Newton's formula expresses when we put the mass [math]dm[/math] of the whole shell. Es decir, podemos evitar una integral y lo haremos. The sum [math]dF[/math] of the módules is [math] dF = G \ \dfrac{m_i \ dm}{r^2} \ \ \ \ \ \ \ \ \ (02) [/math] [math] m_i \ \rightarrow [/math] mass of the part enclosed by the shell of radius [math]r[/math] [math] dm \ \rightarrow [/math] infinitesimal mass of the shell of radius [math]r[/math] The shell of radius [math]r[/math] is in direct contact with the shell located an infinitesimally farther from the center, that is to say situated in [math]r+dr[/math]. Contact involves force transmission in the radial direction. The force points towards the center. That means that the shell located in [math]r+dr[/math] transmits force to the shell located in [math]r[/math]. On the shell located in [math]r[/math] There is an infinitesimal gravitational force, which is added to the infinitesimal from [math]r+dr[/math]. The sum of both is transmitted to [math]r-dr[/math], whose infinitesimal gravitational force is added to the sum of the other two. That means that strength [math]F[/math], exerted on the shell of radius [math]r[/math], it is calculated integrating [math]dF[/math] between [math]r[/math] and [math]R_{_T}[/math] . [math] F= \int_r^{R_{_T}} dF \ \ \ \ \ \ \ \ \ (03) [/math] We apply (02) in (03). [math] F= \int_r^{ R_{_T} } G \ \ \dfrac{m_i \ dm}{r^2} \ \ \ \ \ \ \ \ \ (04) [/math] The density [math]\delta[/math] is uniform. Then we have the following. [math]m_i = \delta \ \dfrac{4}{3} \ \pi \ r^3 \ \ \ \ \ \ \ \ \ (05) [/math] [math]dm = \delta \ 4 \ \pi \ r^2 \ dr \ \ \ \ \ \ \ \ \ (06) [/math] We apply (05) and (06) in (04). [math] F= \int_r^{ R_{_T} } G \ \dfrac{ \delta \ \dfrac{4}{3} \ \pi \ r^3 \ \ \delta \ 4 \ \pi \ r^2 \ dr }{r^2} [/math] [math] F= \dfrac{\left( 4 \ \pi \right)^2 }{3} \ G\ \delta^2 \int_r^{ R_{_T} } \ r^3 \ dr [/math] We solve the integral. [math] F= \dfrac{\left( 4 \ \pi \right)^2 }{3} \ G\ \delta^2 \left[ \dfrac{R_{_T}^4}{4} - \dfrac{r^4}{4} \right] [/math] [math] F= \dfrac{\left( 4 \ \pi \right)^2 }{3} \ G\ \delta^2 \left[ \dfrac{R_{_T}^4}{4} - \dfrac{r^4}{4} \right] [/math] [math] F= \dfrac{4}{3} \ \pi^2 \ G\ \delta^2 \left( R_{_T}^4 - r^4 \right) \ \ \ \ \ \ \ \ \ (07) [/math] The force [math]F[/math] is distributed over the entire spherical surface of radius [math]r[/math] , as previously explained. Then the pressure [math] p [/ math] corresponding to that surface is expressed as follows. [math] p= \dfrac{ \dfrac{4}{3} \ \pi^2 \ G\ \delta^2 \left( R_{_T}^4 - r^4 \right) }{4 \ \pi \ r^2} [/math] [math] p= \dfrac{ \dfrac{4}{3} \ \pi^2 \ G\ \delta^2 \left( R_{_T}^4 - r^4 \right) }{4 \ \pi \ r^2} [/math] [math] p = \dfrac{\pi}{3} \ G \ \delta^2 \ \left( \dfrac{R_{_T}^4}{r^2} - r^2\right) \ \ \ \ \ \ \ \ \ (08) [/math] In (08) we notice the following. If a point B is closer to the center than another point A, that is to say [math]r_{_B} < r_{_A}[/math], then the pressure in B is greater than the pressure in A. That property is independent of the density and the total size of the sphere. In the equation (08) [math] p \rightarrow \infty [/math] when [math]r \rightarrow 0 [/math] . Is that why an absurd or incoherent equation? When you put a model, you are not expressing all the properties of reality. Example. No real cone can have the vertex sufficiently sharp to end in a single point, which meets the ideal of the abstract geometric point, of infinitesimal size or, in practical language, of size equal to zero. The geometric model of the cone assumes that it does. That does not create incoherence in geometric theory. Something similar is found in the ideal model of the sphere. There is a critical region, not suitable for the usual aggregation states. There is no inconsistency. The ideal model exhibits a detail that we can not ignore. The theorems of physics are as abstract as the theoretical geometry. When we are ready to interpret the results well, an infinite tendency in an ideal model means, simply, that there is a border and, in some way, the physical laws avoid going beyond that boundary. Many times the same laws determine the properties of the border. Think of the following ideal model. A material cone is free to move without friction along a straight tube. You place the tube vertically, with the apex of the cone facing down. Although the mass of the cone is very small, say a microgram, the ideal model gives the vertex an infinitesimal surface, equal to zero in practical terms. The weight of a microgram, divided by an infinitesimal surface, gives a pressure tending to infinite. Is the result inconsistent? No. Well interpreted, the model informs that no material cone can have the vertex perfectly sharp, until equaling the abstract geometric point, independently of the mass of the cone. Think of the three usual states of aggregation, gaseous, liquid and solid. Can any of those states exist near the center, where the pressure is too great? Note that [math]p \rightarrow \infty[/math] when [math]r \rightarrow 0[/math]. Too close to the center, the usual aggregation states can not subsist. What kind of state could resist? It would need to be, at the elementary level, a highly dynamic state. We will not advance in this matter, because it exceeds the scope of Newtonian physics. If we knew the maximum pressure that the most resistant of the usual aggregation states can withstand, we could calculate the radius of the central region that neither of these states can occupy. We can do it in the following way. In (08) we can make the following variable change. [math] r^2=u \ \ \ \ \ \ \ \ \ (09) [/math] If in (08) we apply (09) a second degree equation is formed with respect to [math]x[/math]. [math] p = \dfrac{\pi}{3} \ G \ \delta^2 \ \left( \dfrac{R_{_T}^4}{u} - u\right) [/math] We multiply by [math]u[/math] both members. [math] p \ u = \dfrac{\pi}{3} \ G \ \delta^2 \ \left( R_{_T}^4 - u^2 \right) [/math] We divide both members by [math] \dfrac{\pi}{3} \ G \ \delta^2 [/math] . [math] \dfrac{ 3 \ p }{ \pi \ G \ \delta^2 } \ u = R_{_T}^4 - u^2 [/math] We order. [math] u^2+ \dfrac{ 3 \ p }{ \pi \ G \ \delta^2 } \ u - R_{_T}^4 = 0 \ \ \ \ \ \ \ \ \ (10) [/math] The maximum pressure allowed by the most resistant habitual aggregation state is a data independent of the size and density of the sphere. This data could be included in tables, as the constant G . If that data were known, it would suffice to know the density of the sphere to calculate the radius of the critical region, that central region where there can be no gas, liquid, or solid. On the internet there is data from trials that subject substances to increasing pressures, to reach disintegration. When I did the search, a synthetic substance appeared as a substance more resistant to pressure, more resistant than all the known natural substances. A sphere made of that artificial substance, with mass and radius equal to the mass and radius of the Earth, would have a surprisingly large critical region, thousands of kilometers around the center. If the sphere is made of something less resistant than the artificial substance, equation (10) gives a larger critical region.

I have raised the case of an ideal gas. When the collisions are weak and do not modify the internal dynamics of the particles, the behavior of a real monatomic gas approaches that case. In the statement I have defined the force as the pressure multiplied by the surface of the sphere that encloses the gas. If we were to enclose the gas with a spherical latex balloon, it would be the surface of the balloon. It is an impractical but acceptable definition. I have arrived at the following result. [math] \dfrac{ F_{_2} }{ F_{_1} } = \left( \dfrac{ V_{_1} }{ V_{_2} } \right)^{\tfrac{4}{3}} [/math] [math]F_{_2} \ \rightarrow [/math] Force when the volume is [math]V_{_2}[/math] [math]F_{_1} \ \rightarrow [/math] Force when the volume is [math]V_{_1} [/math] We can symbolize [math] V_{_1}[/math] to the initial volume and [math] V_{_2}[/math] to the volume after the compression. It is not the ratio proposed by The Rabid Sloth, but in some cases it may differ little from a relationship inversely proportional to the volume. Recall that this result corresponds to an ideal gas. A real gas could deviate from the result. Could any real gas deviate in the necessary way to fulfill what The Rabid Sloth has proposed? I ignore it. Maybe someone can provide information.

Hi The Rabid Slot. As you have established, compressing is reducing the volume. You have compressed the system to a [math]V_{_1}[/math] volume and, to maintain that constant volume, you need to apply an F1 force. Later you want to reduce the volume an infinitesimal more, that is, you want to get to [math]V_{_2} = V_{_1}-dV[/math]. The force required to keep the volume [math]V_{_2}[/math] constant is a little higher than to maintain [math]V_{_1}[/math], that is, [math]F_{_2} = F_{_1} + dF[/math]. This is the case in systems that are opposed to being compressed, for example a bicycle inflator that has the outlet hole blocked. At first it costs little, then it costs more and more. The same happens when you compress a spring. When you study compression, it is interesting to express that behavior mathematically. When you take a relaxed spring and compress it slightly, you exert force in only one direction and instead of the volume reduction you can measure the length variation of the spring. Hooke's law indicates [math]F_{_2}-F_{_1} = k \left( l_{_2}-l_{_1} \right)[/math], where k is a constant, called the spring constant. Solving the two subtractions as they were defined, remains [math]dF = k \ dl[/math]. Although it is the simplest case, it serves to understand that the variation of size (whether in length or volume) and the variation of force, are related by a mathematical function. Usually the function is expressed as a derivative. [math] \dfrac{dF}{dl} = k \ \ \ \rightarrow[/math] (Hooke's law) [math] \dfrac{dF}{dV} = s \ \ \ \rightarrow[/math] (law of the studied system) Function [math]s[/math] can be mathematically simple or complicated. And you will not know before studying the system physically. If the system is opposed to being compressed, the only thing you know for sure, is that [math]F[/math] grows when the volume decreases. You can not say that the force [math]F[/math] is inversely proportional to volume, since the relationship depends on the type of system. When the volume decreases, the force [math]F[/math] grows in the form determined by the physical laws that the system is fulfilling and by the conditions of the situation.

Yes, it is exercised in all directions. But the plate that regulates the flow is flat and receives force caused by the pressure in a single direction, which is perpendicular to the force necessary to displace the plate. If someone had the obligation to develop this kind of obvious detail before saying a word, we would need centuries to be able to converse. https://www.ncbi.nlm.nih.gov/pubmed/24688733 Is MOSFET some type of transistor? M etal O xide S emiconductor F ield E ffect T ransistor

Citation needed: https://www.technion.ac.il/en/2013/05/technion-scientists-develop-an-advanced-biological-computer/ So an electronic steering system (controlled by a microprocessor) can only steer hard right or hard left, nothing in-between? : The electronic steering system operates in discrete steps. As you said, there is nothing between one step and another. The steps are small enough to offer the driver the feeling of continuous control, although strictly not so. Not the majority of transistors in microprocessors, memories and most of the other components in a computer: Help me understand the concept related to the phrase, to respond.

Hi. Let's go slowly. The question can be interpreted in more context. A context is the current moment, the date in which we live. Today technology is beginning to design and build systems that process information without using the typical resources of electronics. An example that I remember is achieving with bioproteins and other biomolecules the functions that microprocessors do today. And something else. With biomolecules facilitates the attempt to combine the virtues of binary logic with the virtues of fuzzy logic. When the doctor asks where it hurts, touch a point. And you say a little more to the right. In binary logic there is no formulation of a little more to the right. In fuzzy logic it is possible. In the context of computers that use electronic resources, the transistor has been and is a major player. Something like the helmsman on an old ship. Without demerit of the rowers and those who performed other tasks, no old ship could have navigated without a helmsman. Why did the transistor become very important? Imagine a large tank and located quite high. The tank feeds a pipe that carries water down. Inside the pipe there is an adjustable damper, which allows to control the output flow. The tank pressure is exerted in a direction parallel to the pipe. The displacement of the gate is perpendicular to that pressure. Then, the energy needed to regulate the flow is much less than the energy carried by the liquid. The case is analogous to pushing a car. All the weight of the car is exercised vertically and is supported by the street. You push in a horizontal direction and you only need to overcome the friction of the axes. The transistor has 3 terminals, called collector, emitter and base. In the hydraulic analogy, the collector is comparable with the side of the tube connected to the tank. The emitter is comparable to the outlet of the tube. And the base is comparable with the gate that regulates the flow. That is why the control energy, applied to the base, is much lower than the energy conducted between collector and emitter. When you need linear control, there are circuits designed to achieve it. A linear circuit achieves that the current between collector and emitter differs from the control current in only one detail. The value. If the control current is sinusoidal and has a given frequency, the current between collector and emitter is also sinusoidal and has the same frequency, with greater amplitude. This is the base of the amplification that uses transistors. The possibility of controlling the current between collector serves for many applications. The computer data can be encoded as pulses of electrical current. By combining transistors it is possible to design circuits capable of processing logical operations, some simple and others very complex. The transistor allows to use low voltages and has a control terminal that demands very little energy. For that reason it is a remarkable electronic resource.

Thank you very much. Best regards.

Understood. Thanks for moving the thread to this section. Do we have good reasons to dismiss it? Let's do that without the slightest grief and, in reality, with the advantage of knowing that we have eliminated a serious error. Thanks for what you have contributed.

Hi, studiot. The first thing is to admit that you tell the truth. I have no evidence. I only take some data as indications that invite us to examine the subject of the central hole, with hot plasma and ducts towards the poles. I do not want to discard the model without giving it a chance to be examined. 1. I have assumed Newton's gravitational equation to be valid within the planetary body. 2. I have validated Newton's theorem regarding gravity inside a spherical shell of matter. 3. I have assumed that in the radial direction the infinitesimal forces, corresponding to all the points of the segment where the integral is defined, are added. The discrete analogy of that is a set of coins stacked one on top of the other on the table. The table supports the summation of the weights of all the coins. With these criteria we arrive at the equation of pressure at a point within the planetary body. [math]p = \dfrac{\pi}{3} \ G \ \delta^2 \ \left[ \dfrac{R_{_T}^4}{r^2}-r^2 \right][/math] Although the approach is referred to ideal conditions, such as uniform density and perfect spherical symmetry, the shape of the equation reports that when the point has the center the pressure tends to infinity. This ideal result, well interpreted, informs that no material sphere can contain solid, liquid or gaseous matter between the center and a critical radius [math]r_o[/math], because from the center to that radius the pressure overcomes the cohesion of those states. A hot plasma can perfectly work in the central hole and oppose the pressure of matter at the border [math]r_o[/math]. That's why the only thing I can assume is that, if Newton's gravitational equation, Newton's shell theorem and stacked coins are valid, it would be reasonable to think of a hot plasma that occupies the central hole. The plasmas are magnetized and acquire rotational movement, as reported by the following links. https://www.sciencedaily.com/releases/2018/06/180619122949.htm https://vdocuments.mx/documents/plasma-physics.html Magnetization and rotation establish a dynamic axis and an electromagnetic axis, which are not required to be on the same line, but neither do they differ too much. Statistical fluctuations, as reported by these links, produce laser-like effects of short range and with concentrated energy. The electromagnetic axis directs some pulses towards the poles. In that way, by successive pulses, the plasma can dig ducts towards the poles and the pressure fill them with plasma. The temperature of the plasma should decrease towards the poles. The idea of a molten metal core at 6900 ° C in the center of the planet has never facilitated a fully satisfactory reconciliation between observations and physical laws. The idea of the plasma would make conciliation much easier. And the same model would work for all astronomical objects whose approaches approximate spherical symmetry, such as planets, common stars, neutron stars and others. Perhaps it would even facilitate the explanation of the collapse of a supernova, in case that collapse occurs because at a given moment, the material shell is broken by the pressure of the inner plasma. Newton's gravitational equation, Newton's shell theorem and stacked coins. I trust that. The molten metal core causes stumbling in my mind.

Temperature at the Earth's center, auroras, properties of the upper layers of the atmosphere, agree very well with the properties of the plasmas and with what the plasmas are capable of doing. I put a couple of links referring to that. https://www.sciencedaily.com/releases/2018/06/180619122949.htm https://vdocuments.mx/documents/plasma-physics.html

I have calculated the pressure according to the radial coordinate, in the way explained in my second post. That is, integrating the infinitesimal forces between [math]r [/math] and [math]R_{_T}[/math]. I have obtained the following result. [math]p = \dfrac{\pi}{3} \ G \ \delta^2 \ \left[ \dfrac{R_{_T}^4}{r^2}-r^2 \right][/math] In the equation we observe the following. a. For [math]r=R_{_T}[/math] is [math]p=0[/math] . This is logical, because there is no planetary material above the surface of the sphere. b. Regardless of density, [math]p \rightarrow \infty[/math] for [math]r \rightarrow 0[/math] . This happens because the radial force is finite for all the values of the radius. A finite force on a surface tending to zero produces a pressure tending to infinite. My second post exposes the essential detail of the reasoning that leads to that equation. I need that this detail be examined and, if appropriate, criticized, because it leads to the integration of force [math]r[/math] and [math]R_{_T}[/math] . In case that reasoning is wrong, the equation will be invalid. And in case of being successful, all the spheres with finite average density meet the following condition. Between the center and a finite radius [math] r_o [/math] there can be no matter in any of the states of aggregation, solid, liquid or gaseous. That region of radio [math]r_o[/math] it must contain something in another state, which is able to balance the pressure exerted by the rest of the sphere. The most suitable to occupy the central region and balance the pressure of the rest could be a hot plasma. The obtained equation applies to all physical spheres, regardless of size and average density. Although the hole is microscopic, a billiard ball should have something around the center that meets the required condition. It also applies to the Sun, to all the spherical planets, to the Moon, to all the stars, etc. If the only possible thing were hot plasma in the central region, then, in the case of the Sun, the great pressure of the central plasma could have dug a conduit towards each pole, where the hot plasma bristles and spreads around the body forming the crown . Polar auroras are produced on Earth. That perfectly could be emissions of plasma expelled from the center by a pair of conduits that go from the center to the poles, as in the Sun. Why Earth has no hot crown? Because it has less mass than the Sun, the central plasma is in less violent thermodynamic conditions and large-scale statistical fluctuations are less frequent. In the sun they are incessant and maintain a permanent crown. The temperature in the center of the Earth is close to 6900 ºC. The plasma of the solar crown has a temperature close to 6000 ºC. Taking into account that one temperature corresponds to the center of the sphere and the other to the region that surrounds the surface, the little difference of the values is an interesting fact. Whether all this is credible or not depends on the success or failure of the basic reasoning exposed in my second post. That's why I need to examine it.

Thanks for the reference. For doubts, I add the link. https://assets.cambridge.org/97805218/96214/frontmatter/9780521896214_frontmatter.pdf Thanks for the reference.

I understand what you say, because it's reasonable. Beyond that, I prefer to try an abstract mathematical approach, even if it is rudimentary, to then take the tables of known natural and artificial materials, find the material that supports the maximum pressure that matter can support in states of aggregation, put in the final equation the data of our planet, calculate the pressure based on the radius and, finally, find out what happens. Could the maximum pressure supported by states of aggregation be overcome before reaching the center of our planet? Without the calculations we will never know.

Hello, thanks for making you present. I will try to explain the idea better. When there is matter enclosed and subjected to a pressure incompatible with the states of aggregation (solid, liquid, gas), one can assume that this enclosed matter goes to the state of hot plasma and that, that hot plasma, is capable of generating a pressure that balance the gravitational pressure of the material that encloses it. I have tried a rudimentary exploration of the proposal, assuming conditions that simplify the calculation. 1. Planet with uniform density, perfectly spherical. 2. Validity of Newton's gravitational equation within the body of the planet. 3. Validity of the use of continuous variables, to use differentials and integrals. Think of a spherical shell of infinitesimal thickness, whose volume dV is expressed in the following way. [math]dV = 4 \ \pi \ r^2 \ dr \ \ \ \ \ \ \ \ \ (01)[/math] [math]r \ \rightarrow[/math] radius of the infinitesimal shell Symbolize P to a point on the shell of radius r. We want to calculate the gravitational force at that point. The point P is inside the finite shell between [math]r[/math] and [math]R_{_T}[/math]. Newton demonstrated that a closed shell of matter, independent of the form, exerts net gravitational force equal to zero in all points of the inner region. A similar theorem exists for the electrostatic force within a closed shell. That means that the force of gravity on P depends only on the sphere between the center of the planet and the radius [math]r[/math]. Now we need to reason something. Think of a radius of the planet, which extends from the center to the planetary surface. That radius contains infinite points. Each one fulfills the conditions of point P, for a determined value of the radius. Think of 3 contiguous points, [math]P_{_1},P_{_2},P_{_3}[/math]. At [math]P_{_1}[/math] there is an infinitesimal force, at [math]P_{_2}[/math] other and [math]P_{_3}[/math] another. In gross language, we can say that [math]P_{_1}[/math] and [math]P_{_2}[/math] are touching. The same [math]P_{_2}[/math] and [math]P_{_3}[/math]. In a little more precise language, we can say that between two contiguous points are the quantum interactions, which are responsible for transmitting and adding, in radial direction, the infinitesimal forces of all points [math]P_i[/math]. What does this mean ? If we have reasoned well, it means that the force at a point P is the sum of the infinitesimal forces of the points between r and [math]R_{_T}[/math], belonging to the same radial segment that contains P. In coarse language, the force at a point P is calculated by adding, in the radial direction, the infinitesimal force of P with all the infinitesimals of the points between P and the planetary surface. Is there a contradiction between Newton's theorem and the sum of infinitesimals in the radial direction? The theorem corresponds to a closed shell whose interior is empty. The net force is zero at the points of the interior vacuum. The inside of the shell that we are defining on the planet is not empty. Then there is something that transmits force and the infinitesimals add up in a radial direction. The spherical symmetry of Newton's theorem also exists on the planet. For Newton's gravitational formula, the only mass causing net force is the mass contained between the center of the planet and the radius r. I would like to receive opinions regarding that reasoning. If appropriate, we can advance a little more in the mathematical approach.

Hi. Some questions have been installed in my head. 1. In what is transformed a material subjected to a pressure that overcomes the atomic cohesion? 2. There are tables dedicated to the maximum pressure that each material supports without losing its basic constitution. 3. There are enough data on our planet and other astronomical objects to calculate the pressure as a function of the radial coordinate, inside the body of the object. In the case of our planet, it would be the pressure at a point below the planetary surface. 4. Is there any known material, natural or artificial, capable of withstanding the pressure in points that are deeper than a certain limit? I'm thinking of putting up with the pressure without atomic cohesion being overcome. 5. Could we formulate the pressure according to the radial coordinate? 6. Can there be a region, around the center of the planet, where solid, liquid and gaseous states are impossible, so that the only state able to withstand the pressure is plasma? That is, the area closest to the center is occupied by plasma.

Within the concert of ideas of the cosmological community, are the adjectives dark and undetected synonymous? Example without pretense of taking it seriously. A cloud of positrons, in thermal equilibrium with the microwave background, would be indistinguishable from that background for typical observation methods. It is not a dark cloud. It irradiates the thermal spectrum corresponding to the equilibrium temperature, but what radiates is identical to the cosmic background and by the usual means is indistinguishable. Now I think about it and I notice that, from time to time, some of those clouds would collapse producing a burst of gamma rays, like those called explosive sources of gamma rays. But I only put it to give an idea of how something present can be indistinguishable.