ALine

Doesn't gamma radiation strip neutrons from atoms?

Wouldn't the proton pair be past the coulomb barrier between the two? So would it be feasible?

Could you take alpha radiation and then strip the neutrons from it using gamma radiation and then apply radiation to heat the proton pair to lead to fusion?

I believe to have found a pattern for the goldbach conjecture, however I need help formalizing it into an equation and proof.

Just wanted to make sure everyone was doing ok and wanted to say hello.

I was working trying to figure out how to map input to output and came up with this program.

def create_mapping_function(inputData, outputData):
    mapping = []
    # map the same to the same
    for i in range(0,len(inputData)):
        for o in range(0,len(outputData)):
            if outputData[o] == inputData[i]:
                # mapping position to position
                # this shows the mapping values.
                mapping.append([i,o])
    return mapping

inputData = input_data()
outputData = output_data()


mapping = create_mapping_function(inputData, outputData)

# print(f)

# use mapping and save them as a mapping function.

inputData    = ['h','e','l','l','o']

# mapping   = f
# # input a unique list with a specific length
#f(x)
def mapping_function(inputData, mapping):
    outputData = []
    for i in range(0,len(inputData)):
        outputData.append(0) # placeholders

    for i in range(0,len(inputData)):
        outputData[mapping[i][1]] = inputData[mapping[i][0]]

    return outputData

output = mapping_function(inputData, mapping)
print(output)

Here is an image of the prototype...

I received a multimeter read out before and after exposing it to the sun and got an increase in voltage over time.

I "think" it works on a principle similar to osmosis but with electrons, however I am most certain this may be wrong.

I developed and prototype for an invention for collecting energy from the sun.

It stores a maximum of .6V. It is very inefficient and I feel as though the prototype can be improved dramatically.

(A novel invention for collecting energy from the sun.) <- real title

dang, thought it was a double scale.

this is indeed a puzzle

Does there have to be real and fake coins? Like their have to be bags which are real and fake? Can you have all 5 bags be fake and none real?

hmmm, what type of weighing scale?

I was about to finish, but then I saw this trickster.

2 hours ago, Genady said:

by weighing only once.

Now do you mean weighing every bag all together once or can I weigh each bag independently once.

now when you say "all the coins in some bags are real and all the coins in other bags are fake." Do you mean that their are no empty bags and there are also no bags which are heterogeneous. Or that they have real and fake coins?

I have been thinking about how you could probe within a map or function in algebra and decided to try to use a sort of "probe" set in-between the sets that are being mapped together. It reminds me of composition and am trying it from that angle, however I need some help with it. The reason I want to do this is because I want to see if I can "discover" a mapping without the need of a mapping(for higher order math's) or function equation for algebra right now.

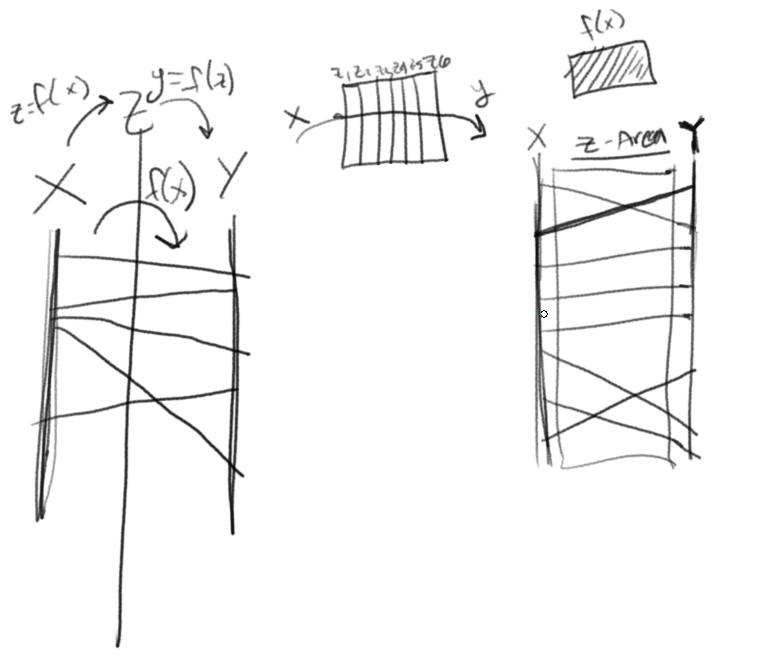
The name could use some work for the topic.

was just spit balling @joigus

thank you

52 minutes ago, studiot said:

Does 4 implies 2 have any meaning?

How do mathematicians define "meaning?" Because whenever I run into it I come to an existential road block.

But, yes I think I understand what you are saying in terms of Relations and my intuitive thought.

I think I got function and relation confused and did not understand each of there definitions are you have pointed out prior.

Random thought, could this be used to imply symmetry breaking in a field of study such as physics?

6 minutes ago, studiot said:

a R b denotes that b is related to a

Are relations the same as if conditional statements then? Or at the very least similar? Because with a if b, you have b -> a.

5 minutes ago, studiot said:

What do you mean by this ?

I mean to say that a relationship is the connection between two points in space in nature.

Also I mean a relationship is an object in math.

4 minutes ago, wtf said:

But the implication is manifestly false, as I noted. If X and Y have the same truth value, then their xnor is true and their xor is false, resulting in a false material implication. Agree or disagree?

Agree

4 minutes ago, wtf said:

Didn't understand this. Sets of knowledge? What do you mean?

Just expressing my limited amount of knowledge on the subject.

5 minutes ago, wtf said:

But the implication is manifestly false, as I noted. If X and Y have the same truth value, then their xnor is true and their xor is false, resulting in a false material implication. Agree or disagree?

Need some time to try and formalize this, have problems with this endeavor.

I admit defeat.

6 minutes ago, ALine said:

(relationship) [ X XOR Y -> X XNOR Y] (this was the first way I thought about doing it where XOR was the addition in mathematics because of the circle and the +, multiplication would be circle and x.

 

It being I have no idea how to formally explain it.

It being my idea/discovery.

Mathematics is the structuring of the universe, ergo nature, into a set of discoverable rules and formulations. These formulations are conceived by the human mind. A set is itself an inverse of reality due to those languages which better describe reality. Languages, of the romantic kind, describe humans endeavor to discern between the reality and fictitious efforts of noise. That's probably the best way I can put my discovery. I think I am trying to describe automata theory. Not sure though. Please help.

(relationship) [ X XOR Y -> X XNOR Y] (this was the first way I thought about doing it where XOR was the addition in mathematics because of the circle and the +, multiplication would be circle and x.

41 minutes ago, wtf said:

So, what do you mean by -> here?

I was using implication here.

41 minutes ago, wtf said:

Mathematical functions never create news sets. Given two sets, there may be functions between them. But the sets have to already exist. Functions do relate them in terms of inputs and outputs, but this isn't a very meaningful way to put it.

I may have been applying my sets of knowledge to a field of study which uses mathematics to make the above statement true.

44 minutes ago, wtf said:

symmetric addition

XOR Gate symmetric difference,

XNOR Gate symmetric addition, however I worded it wrong.

58 minutes ago, wtf said:

Secondly, Russell showed in 1901 that there is no universal set. Are you working with some restricted universe of sets? Can you clarify what you mean by universal set?

jesus math is old. Was not aware of this fact. Thanks for this.

58 minutes ago, wtf said:

Potentially a fractal

This was just banter more than stating any claims or facts.

Thanks for your responses.

This basis of the idea was that the implication emerged from the relationship.

X, being a set, and Y being a set.

X XNOR Y -> X XOR Y, is the basis of mathematics.

Mathematics, based on my research, is about relationships which can be described using functions. These functions relate or create new sets. However there is a problem. What actually IS a relationship.

Claim: A relationship is a symmetric difference -> symmetric addition.

Explanation: A symmetric addition is a similarity between two sets. It is a comparison between these two sets and everything else in the universal set. By comparing both obtain something neat.

Potentially a fractal. This is as far as I have gotten on the problem. 

11 minutes ago, wtf said:

Was this for me?

A TM program is a finite sequence of symbols taken from an at most countably infinite alphabet. There are therefore at most countably many TM programs of length 1, countably many of length 2, countably many of length 3, and so forth. The countable union of countably many sets is countable. Therefore there are at most a countable infinity of TMs. And for TMs you can substitute programs in any Turing-complete language: FORTRAN, COBOL, Python, C++, or whatever.

Since there are uncountably many sets of natural numbers (per Cantor), there must necessarily be sets of natural numbers whose members can NOT be generated by any computer program. That contradicts your claim, to the extent that I can interpret it.

https://en.wikipedia.org/wiki/Turing_machine

This does not, by the way, contradict your thesis. Your premises are wrong but your conclusion is right! A step in a computer program is a transition from one state of the computer's hardware to some other state. Practical computers -- real-life digital computers implemented physically -- are finite state machines. They make a succession of transformations from one state to another, and those transitions can be taken to be mathematical functions.

https://en.wikipedia.org/wiki/Finite-state_machine

 

 

yes, apologies

Can you provide an explanation to your Turing machine statement please.

Thanks bud