Trurl

Studiot, when you recommended Mark Levi’s book did you see a parallel in that it was as confusing as my posts? I mean the guy is a mathematician and physicist so he is more skilled than me. The majority of reviews are 5 stars. But the text was not user friendly. It is...proof...diagram...proof with one or two sentences to explain. It would take me hours each proof to find out what he is talking about. And he said you only need geometry. I could take his word the proofs work, but wouldn’t that defeat the purpose? I loved the first chapter where he was going to relate pure math to physics. But I couldn’t make it past the second chapter. I looked ahead and I have no clue what direction he is comparing math and physics. If my posts are explained this poorly (or worse), I have to fix it. I need to define my ideas like a textbook would. Like Levi’s book, he may have the best relation of practical science and pure mathematics, but if it takes months to recreate his work, no wonder my ideas are not clear. I am working on a clear write-up. There is so much information it will take weeks.

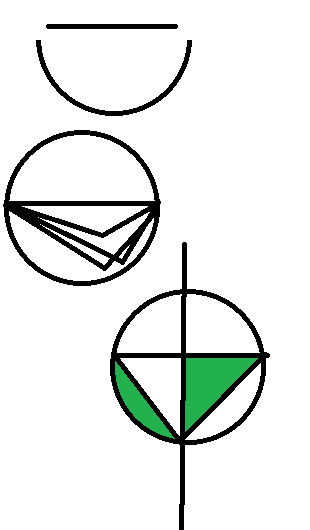
Thanks Studious. I am going to get that book. I think it will help me communicate ideas. No one knows what I am saying. The ideas might just be too abstract. I thought the 4 equations were concrete. But you are right I have to come up with something tangible. One clear example. I included a PDF in the last post you read. Is that any help? I do have the second part of my write-up. I am aware the following hypothesis most likely don’t work, but do you get any ideas when you read them? I am describing geometry. Easy enough to make a hypothesis, but I have not been successful. When you read them, do they make any sense? Other examples of my hypothesizes. I want to post all the content. I will not post again until I have a concrete example. The attached PDF of my other hypothesis shows a parabola and an example of 64 degrees by a triangle with sides 3 and 5. If the right eyes see it, I believe it could be turned into something powerful. So please excuse these hypothesizes. It is related, but I can't explain it. P.S. The reason I originally called it the 2 Sided Triangle was to spark interest. You are right people couldn't get over the name. Also pnp is what it has always been in this post. PNP is the given semi-Prime. I am placing into a triangle pnp and its factors x and y. It would be extremely useful. But it relies on the fact that we can use the equations I derived to find x. Which we can if pnp is small. Try the 4 equations for known semi-Primes. My hypothesizes are what you can do once x is found. I also hypothesize if all sides of the triangle equaled pnp, x, and y. It is possible to draw such a triangle. There are infinite triangles, but I want to find what angle between x and y will produce side of pnp. This post is already too long. I will post when I have a clear example. Or to answer questions. All this ties in. And maybe if I explain it right I can make you believe. The following is a post I was working on before I read the replies. So something repeat. Ok here is a short but powerful idea. I think we should write as many hypotheses as we can. A free writing exercise like Mark Levy’s book. A brainstorming session that is serious and not silly. Of course, some of you may find my hypothesis silly. In Stanislaw Lem’s book Futurological Congress it briefly mentions the futurists who study what words will be used in the future to determine the technology the future has. But this hypothesis is simple, but I know my drawings stink. If anyone knows a program to create traditional drafting and geometry please share. Adobe Creative Cloud is a scam. Ok here is my hypothesis: You see a line in the first figure of the attached drawing. This line is length pnp. There is a half-circle below it. In drawing 2 there are three angles in the half-circles. These are the triangles whose largest side is pnp. They are many, but the angles must touch both ends of pnp. The third drawing is an isosceles triangle. (The isosceles triangle is half white and half green.) It is drawn in this way because we only have test triangles (angles) who fall in the green area. These angles still have to touch both sides of pnp, but we only test those areas in green because of redundancy. If one segment of the triangle is large the other is short the lengths will repeat after half the distance has been covered. (I hope this makes sense. I need help with the development of this idea.) That is it. Just picture only using some of the circle and relate it to finding angles on the parabola of the previous post hypothesis. Abstract hypothesis (Just for fun.): The Riemann Hypothesis to prove or disprove there is a zero we can use a triangle who has factors as its segments. I believe ½ is a critical line where the zeros occur because the factors are on an isosceles triangle. The sides are equal and cancel each other. Dealing with fractions so we cannot have division by zero. I do not know enough about the Riemann Hypothesis to describe further. But this is just a brainstorm I had. I know its silly, but I just wanted to share the idea. See attached picture. When you use the 4 equations in this thread to find x from pnp, x occurs closer to the left-hand side of the number line. My future concentration will be on determining x perfectly. Maybe if we apply only the green area on the circle to searching for x possibilities, we might will solve semi-Primes with geometry. I am aware my hypothesizes seem absurd. But that is how I formed the 4 equations I posted on this thread. I think there should be a math class on nothing but forming hypothesizes. I do not mean the hypothesis shouldn’t be well thought out. It may even be to an impossible problem. But I just read Mark Levy’s book on free writing and I want to do math free writing. But often choosing a math problem to work on is just as important as solving it.

Ok, this post has many views no comments on my new hypothesis. I do understand that it may be that no one is exactly sure what it is I am doing. I am not doing one thing in this post. The goal was to present my equations that solve for x knowing only pnp. I think we can agree that the equations are significant, but to find a practical solution we need the ability to solve large numbers. What works for 5 and 17 is easy to solve, but advanced computer programming is needed to crunch a 100-digit number. I am trying to improve my ability of explaining mathematical subjects. I just finished reading the book Accidental Genus by Mark Levy. It dealt with producing content. I got content but I need to communicate my ideas. I believe explaining math is a skill that improves with practice. But sometimes a math solution is hard to explain or prove why it works and how we got there. And it does not help that most U.S. citizens are math illiterate. So, you show your work to those who do and prepare for criticism. I wrote “this problem can be solved with elementary mathematics,” in a lesson outline. And my instructor wrote back “this isn’t elementary mathematics.” I meant math below calculus. It was only one phrase out of a 5-page document. My material did not rely on this phrase. But it was enough to make her very mad and pick apart my lesson plan. So that is where I am at. I’m sure if I had a person-to-person conversation with someone, I could explain my work. Using diagrams and paragraphs by themselves is a challenge. But I did not write this post just to babble. I want you to look at the attached pdf and see if it has any merit. In it I claim that I can solve a triangle knowing only 2 sides. Yes, with that title no one will bother to look at it. But spoiler alert I draw the triangle that with only 2 sides known with the characteristics I want it to have. Yes, I know only 2 sides has infinitely possibilities. But does it? What if we add more information? Perhaps the hypothesis I just posted. For example, what if you have a side of the triangle that is a product of the 2 sides? I know that sentence makes sense to me and not you, but what if we design a set of custom triangles? So that is what I meant. It still may not work, but I am working on a geometric drawing that may tie the 2 together. I am writing it up now. But it is important that I accurately communicate my idea. Simply put this is it: I believe there are vector “factors”, 2 sides of a triangle that through vector summation result in the pnp side (the known vector resultant). So, if we can find a way to relate vector sum to the factors of the scalar of resultant, we can factor pnp into 2 semi-Prime products. And since pnp is semi-Prime only one set of products were work. **This does not mean that a semi-Prime vector resultant would not have infinite many solutions. Instead, the vector sum with the Prime products, would be unique. And since it is unique, we may be able to predict or design where it occurs. **Again, this hypothesis probably makes sense to me and not you, the reader. But what does it make you think? It is hard for me to describe something where no source to reference. But any feedback is helpful. The goal is not to produce a theory, but to explain to you, the reader my reasoning. If you are interested of all in my hypothesis, review the attached PDF. I will later attempt to explain why I brought up this subject again. 2sided_triangle20210528SFN.pdf

Ok I’m going to bounce an idea off you. If it is total wrong it doesn’t mean it isn’t important. I began my work on Semi-Primes years ago with a vision that a logarithmic spiral could show a pattern in Prime numbers. I have heard others say this, but they were talking a scatter plot while I tried to make my spirals characteristics match the properties of the Prime numbers. And of course, it is easy to say a logarithmic spiral will show a pattern, but finding the pattern is the challenge. I attempted several attempts without success. The Hypothesis: If you draw an angle between 2 lines of length of 2 Prime numbers the vector result is a length of the Semi-Prime perhaps a pattern will form in that the spiral that encompasses the end point of the vector result will form a logarithmic spiral. A spiral that can be described mathematically on both the coordinate plane and the equation of a logarithmic spiral. If we know the angle between the 2 Prime numbers and the vector resultant we know all sides of the vector triangle. We also know the slope of the vector resultant and its vector magnitude. The slope or derivative can be used to predict future values. There is a problem determining if a number is Prime or a Semi-Prime. The 4 equations I listed on this thread should only work if both x and y are Prime and when x*y = pnp. Multiplying an unknown factor by a known Prime and placing in my equations may become a way to test for Primality. If the equation produces correct factors we know both x and y are Prime numbers. Also, there are infinitely many Prime numbers so there are infinitely many corresponding factors for x. For example 3 *5 or 3 *7 or 3 *11. For every Prime factor there is a Prime that can be multiple to produce a Semi-Prime. Multiplying 3 by a larger Prime factor will produce a Semi-Prime that will increase in magnitude. **Just to be clear on the triangle I am drawing. I envision a vector with sides of the Prime factors. The angle between them will determined by SSS from the Prime number factors and pnp as the vector resultant. I propose that if we graph this for all known Semi-Primes a pattern (a useful pattern will result.) Again, I am aware that this is easier said than done. I cannot calculate this by myself. But I propose that treating Semi-Primes in vector form will lead to better mathematical representation.

If you are interested in these equations visit my status page. i stink at writing for mathematics. So much for publishing a textbook. My education professors said I was writing musings for the internet. It may not seem like it but I have an undergraduate understanding of math. I enjoy reading Michio Kaku’s books. String theory is pure math. I love plugging numbers. Can anyone suggest a site with string theory math for the novice? From what I understand the math of modern physics is out of control. Anyways enjoy the link in about me page. Can anyone recommend a book about writing for mathematics?

Good eye. x = Sqrt[ [ ((x^2 * pnp^4 + 2 * pnp^2 * x^5) + x^8) / pnp^4]]

Here is my previous attempt at a perfect equation to find semi-Primes. The trouble is that it is too complex to solve easily. x = Sqrt[ [ ((x^2 * pnp^4 + 2 * pnp^2 * x^5) + x^8 / pnp^4]] [pnp^4 = [[ ( (pnp^4 * x^2 + 2 * pnp^2 * x^5) )] / x^2 ] – [(x^3 / pnp / 2)] Test these equations. If you want to know how they were derived pm me and I will send you a link to download free. I don’t mean to advertise, but if you are interested pm me. It is the easiest way to get you a lot of information.

I am only kidding. I did not think of it either. My nephew said he had a friend that did math on excel and mathematics. But it didn't click because they never taught that in school. I was watching a video of The Great Courses and the instructor showed how computers solve differential equations. It is a cheap and powerful method. But it may be able to graph from 0 to pnp.

One more post before I conclude this project. Why did no one recommend Excel for the graph and the list? It would graph and list an N of 100 digits easily. It has a segment of adjustable accuracy. Spread sheets are common to solve graphs and differential equations and it is a tool everyone has access to. It would take more adjustments with Mathematica. Of course if you didn’t believe in my work you wouldn’t mention this simple tool. However if you think it can be estimated with a simple graph you have already plugged it into the spreadsheet without sharing.

Lock this thread. I have spent years reading encryption books and tinkering with Prime numbers. It was very valuable in that I could study statistics, game theory, review calculus and work on ideas. It was more than just crunching x’s and pnp’s. That is why I keep it up. I even learned the basics of Mathematica. My end result was to approximate x by graphing a pattern in division. I need to know what x will have a y value of N. I can’t graph it accurately enough with standard programs. I don’t know if there are any computer programs to graph a range that is pnp. I could take guess at the value and solve within 20 guesses, but I really thought the graph was possible. I am on to other projects. I am really interested on the brilliant, but common sense experiments of the early 1900’s. I am amazed how all the experiments in light and electricity were common place in those scientists’ labs. I have a physics experiment book that is at the undergrade level. I think I’ll follow along and recreate the experiments. So all my work and I can only approximate x. It’s not wasted time. I learned a lot. But if anyone has some more advanced graphing software plug my numbers in please.

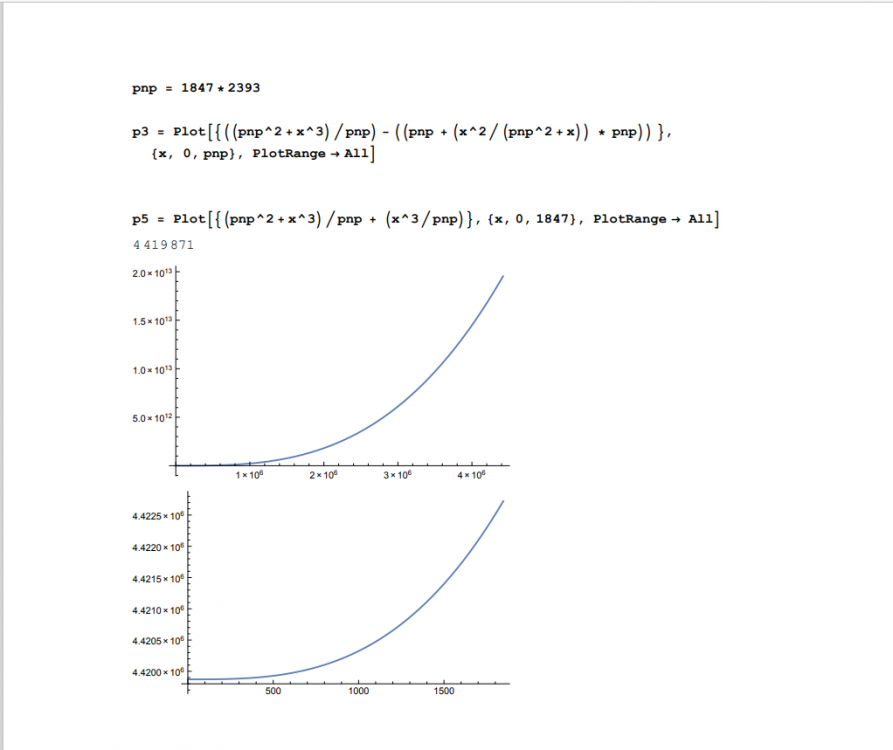
p3 = ((pnp^2 + x^3) / pnp) – ((pnp + (x^2 / (pnp^2 + x)) * pnp)) p5 = (pnp^2 + x^3) / pnp + (x^3 / pnp) where N = pnp for computer computation Given equations p3 and p5. p3 is equal to p5 a distance of N. Since N is the distance subtracted from p5 So, p3(x_semiPrime)=0 and p5(x_semiPrime)=N That is y=0 at an x equal to the smaller semi-Prime at p3. And at p5, y=N. Knowing the above, p3(x) = p5(x+N) so p3(N)=p5(N+N) since these equal the derivative of those should also equal p3’(x) = p5’(N) and p3’(N) = p5’(N+N) My goal is to get enough “given” information to form a solvable deferential equation. I find it to be challenging if not outright confusing. I subtracted p5 by another equation with value N to get p3. I thought it translated the x-axis values to the y-axis. However it has shifted the equation a value of N in the x-axis to the left. I believe the above statements are correct. Are they enough to create a solvable differential equation?

Both good explanations. I don’t know what to think of multiple realities. With all the histories and multiple realities, we forget we are living it. Our lives are just as significant as any reality.

In Star Trek Next Generation the last episode “All Good Things,” the character Que, an omnipotent being, suggest the crew was not in space to map constellations. But all our physical sciences are based on these observations, So my question is what is Que suggesting?

Ok, I hope this makes sense. It is only an idea. I just wanted to post it to see if it makes anyone else see something new in a plain graph. I had trouble finding the values on the graph of x when N is a hundred-digit number. I was certain that I could just zoom in or pan the graph to see the proper value. As I have found, this is difficult to do in practice. So I am back at just approximating x and using test values. But in trying to do this I noticed something else that would help in the search for x knowing only N. So for N = x *y, where x and y are 2 unknown Prime numbers, there exists a pattern. (I hope you can understand the following algebra.) (x^2/y) = (X^3/N) = ((N/(y^2/x)) So with a x of 5 and a y of 17 and an N of 85 we have: (25/17) = (125/85) = (85/57.8) = 1.470588 This should be true only of semiPrimes. It is interesting to so values of inequalities in the x axis. (x^2/y) < x < y < (y^2/x) < N < (N+(x^3/N)) I hypothesized if I transformed the y and x axis for equation p5 I would have a clear plot. Because a value of y would be known to be N. I have tried the function Parametric Plot. I haven’t found software that defines x knowing a known range. So my hypothesis is this: My equations are based on the value N. If I were to take equation p5 and subtract in by itself, I would have N-N or zero. But what I now have is the equation of p3. So I just translated the graph N in the negative direction. Then from the result, I add (x^2/y) along the x-axis and the y value at this x value will be x. So for 85=5*17 the y value of equation p3 will equal 5 where the x value equals 1.47. There is still much to be worked out. Please check my logic. And please don’t kill my post. I am being serious. Doing math is one thing. Explaining it is another. But if this works I have just transformed axis using only basic algebra. I think it will be useful to find x knowing only N.

Ok, so I graphed the RSA 100. There is one problem in particular. I just can’t read the axis’ scale. I am researching how to evaluate the graph in Mathematica. I just need to find xongraph where yongraph equals pnp. That would be the range. I believe you can test for yongraph on a graphing calculator and find points on the graph. I post this as a mathematical challenge to the SFN community. How do I arrange the scales in mathematic software to find the y value I am looking for? It takes milliseconds to draw, but I need to be able to evaluate it.

For a large N use a software like Mathematica and paste in N. Yes I know math types don’t like that. I apologize. It just needs some properties as an algorithm. So in the following Mathematica code replace pnp with N and graph and look for a yonthegraph of pnp. Work from the left side. I don’t know it’s speed compared to other methods. The truth is I don’t know the other methods. I know they rely on series. I took a simpler approach and looked for patterns in the division of semiPrimes. My question does it work for all factor, not just factors of semiPrimes? Refer to my second post of this thread. i am going to rewrite the proof so every can understand it. (Not just me.) i think the confusion is people are looking for a number series and I am just doing algebraic operations.

Here is the summary of my work: The main equation is: (N^2+x^3)/N = N+[(x^2/((N^2/x)+x))*N] All the other math is the simplification of this equation. If you simplify the equation completely it results in zero equals zero. Which is not particularly useful. But we can put N the given semiprime product of x and y, where x and y are the Prime factors. As I have showed in the examples if you “plug and chug” “N” into the equation and graph the equation in its un-simplified form, then my hypothesis says that reading the graph in how I told you to read p3 and p5 should reveal x knowing only N. Test it. Plug in N and x. Or just graph it. You will find it works for any size N. And that graphing is in polynomial time. But if you do not believe me, then please tell me your reasoning. I know the way I wrote my proof to you was hard to understand. Explaining is much more difficult than solving. I tried to word the proof how I thought it through, but if no one understands it, it is not helpful.

PNP is the variable name of the semiPrime in question. It is the given. It is usually referred to as N as in N=p*q, where p and q are the Prime number factors. PNP is my name because I cannot call it N because N is a keyword in Mathematica. PNP or N is the factor of 2 Primes and is the given in RSA cryptography. Finding x knowing only N is considered difficult with large Prime factors. The goal of this work is to use a simple mathematical pattern to list N in terms of x, than reveal the value of x in the graph of the equations. So basically, if you did not understand my write up, you could plug and chug PNP into my equations p3 and p5 and they would both reveal x, the smaller Prime factor at: for p3 where y (y of the graph) =0 for p5 where y equals N (again y of the graph) i should have have started by explaining it that way, but I wanted to show to some extent, how the equations where simply derived. It will take me some time to address the other questions.

PNP is N in this. Originally it was N = p*j. But N is protected in Mathematica so I renamed it pnp. N = p*J = x*y, because I also called p, x and j, y. This is a poor decision because when you graph it ygraph is different from y in the equation. So it created some confusion, but writing this up and coming up with a solution variables get jumbled. DLP is the discrete logarithmic problem. If this can factor semi-Primes then the DLP is next to go. Remember I am claiming I can factor semi-Primes and thus RSA cryptography would be no more. But it wouldn't matter because other cryptosystems would take its place. I know that is a bold claim. But I am only looking at simple patterns in factoring. Here is a draft write-up I was working on. I hope it helps and not hinders. Finding math is one challenge. Explaining it is another. Hacking extends to all disciplines and is not limited to technology. The question I ask is can math be hacked? Is there a “math hack” that will solve problems? The number guessing game is a programming exercise for those learning to program. The user of the program guesses a number and is told if their guess is higher or lower than the desired value. It is very efficient and often takes less than ten guesses to find a number with several digits of length. Factoring is a problem of cryptography. The most common example is finding the Prime factors of very large numbers. Yes, this is an impossible math problem. But what if we take what is known about the number guessing game and apply it to find the smaller Prime factor? Here I attempt to demonstrate how a series of guesses can eliminate possible factors. Definitions: N is the number that is known and the number we will factor. (Or estimate the equation is equal to.) x is the smaller factor. We will plug this number in for a guess. The guess is found when N calculated is within range of the known N. y is the larger factor number. We will place it terms of x to build the equations. We start with 3 sample equations: Equation 1: N = xy Equation 2: y = Sqrt[(((N^2) / x) – x^2)) / x] Equation 3: y = (((N^2/x) + x^2) / N) ** In case you are wondering how these equations are derived, it is simply finding a pattern in y and putting it in terms of x. ** Also note Equation 2 and 3 are equal. They stand alone when we guess. It only takes Equation 2 or Equation 3 to make a guess. We know N and will place a test x into the equation: N = [Equation 2] * x Or N = Sqrt[(((N^2) / x) – x^2)) / x] * x **Do not simplify further. The rules of simplification results in an imaginary number. Remember we are just guessing there will not be a perfect solution. Test N = 25, 135,039 Place into equation and use a test x of 5500. So that 5500 is the test x. 25135039 = Sqrt[(((25135039^2) / 5500 – 5500^2) / 5500)] * 5500 25135039 != 25131729.1592027 The guess on the right side of the equation is larger than the Given N. N does not equal N. So we must decrease the test value x. The value 5500 for x creates to small a number. NGiven > NGuess So we will try a test value of 2500. N = Sqrt[((N^2) – x^2)) / x] * x 25135039 = Sqrt[(((25135039^2) / 2500 – 2500^2) / 2500)] *2500 25135039 >25134728.17699 This is very close. NGiven is still greater than NGuess. But it is still within error. We would continue the process until we test an x of approximate value 3581. 25135039 = Sqrt[(((25135039^2) / 3581 – 3581^2) / 3581)] *3581 Which equals 7018.440204 * 3581 25135039 is close to 25134125.4942275 Then we divide NGiven by x and have 25135039/ 3581 = y = 7019 Well we tested the value of x = 3581 because we know the answer. I know what you are thinking that is a difference of plus or minus 1000. But N is 8 digits in magnitude. There is another test: Equation 3. You see, setting y in terms of x is quite easy. There are easily dozens such equations. Now we test 2500 and 3581 again using Equation 3. y = (((N^2/x) + x^2) / N) N = (((N^2/x) + x^2) / N) * x For x = 2500 N = (((N^2/x) + x^2) / N) * x N = (((25,135,039^2/2500) + 2500^2) / 25,135,039) *2500 25,135,039 is approximated by 25,135,660.6421 Is it too close to call again? Did we narrow it done to only 1000 odd numbers we have to test? Place in a test x of 3518: N = (((25,135,039^2/3581) + 3581^2) / 25,135,039) *3581 25,135,039 is approximated by 25,136,865.98 Simple equations that are easy to plug and chug withing a few minutes. The guessing game requires a math program. I use Mathematica to guess and 128-bit Prime numbers. I still do not know if it is simplified enough to prove useful. It is a math hack. Traditional math would want proofs and an equation that gave a perfect solution. But it does make sense that there are patterns in factorization. A number has 2 factors, say x and y. If you increase y then x must decrease. So there are patterns. The challenge is to describe those patterns with a math description. https://github.com/Craylar/Patterns-in-Factorization Equation 3: y = (((N^2/x) + x^2) / N) N = (((N^2/x) + x^2) / N) * x, which reduces to (N^2 + x^3)/N = N which we know is not true. The error is (x^3/N) So, (N^2 + x^3)/N = N + (x^3/N) ** (N^2 + x^3)/N = N + (x^3/N) We know from discovery that (x^3/N) = (x^2/y) **Will explain further. So we substitute for y in terms of x The simplest substitution is (y=N/x) (For another equation we could substitute: (y=(N^2/x)+x^2/N) The goal is to use as simple equation that can be graphed. (That is in terms of the know N in terms of x.) It is irrelevant that we cannot simplify or solve the equations. It is a “math hack.” We use the graph to find x in polynomial time. Another equation in terms of y is: (y=(N^2/x + x^2)/N). This can also be substitute into (x^3/N) = (x^2/y), and graphed. **

I know I not the best math teacher. What parts do you not understand? I am taking the known semiPrime, PNP, and graphing it along the x axis to find the place where y equals zero. I do this to find x knowing only PNP. Look at the pdf I posted (see previous post attachment). You will see 2 equations, p3 and P5, and the graphs that correspond to them there. N=1847*2393=4419871=4.4199871*10^6. (These are N=x*y as an example) For p3 as y approaches 0, x will be 1847 or x. For p5 as x approaches 1847, y=4.4199871*10^6 or N (here x at 1847 y=N because the equation is structured differently. Also note y in N=x*y is distinct from y on the graph.) I know that my equations are confusing. I was trying to show how they were derived algebraically. For now forget the equations and focus on the graph. I recommend using a computer software to graph equations p3 and P5. Trust me this is not a super advanced math problem. Stop treating it as such and go with you graph reading skills. That is why I called it simple yet interesting. Sometimes the simplest solution is best. Let me know if this is a better description. And remember I use N and PNP to mean the same N=PNP.

Thoughts? Do you believe the math? I’ve shared it with an engineer and he thought it worked but he said he wasn’t a mathematician. I am not a mathematician either. And I am biased. I envisioned it so it makes sense to me. I was hoping for some guidance from these boards. Is it worth publishing? I am not an elite mathematician so message boards and the net are where I publish. So now break large semiPrimes. And if the math holds true, break the DLP next. Primality test by multiplication and seeing if a semiPrime is formed. There are no prizes for factoring anymore. Patterns in the graphs; a normal distribution. The maths range from algebra to calculus. There are similarities to graphing differential equations. So if you believe in my math please let me know. The message boards were built to solve problems like these.

The graph is what’s important. N=1847*2393=4419871=4.4199871*10^6 For p3 as y approaches 0, x will be 1847 or x. For p5 as x approaches 1847, y=4.4199871*10^6 or N Using graphing in polynomial time to get an answer that algebra can’t solve.

(N^2 + x^3)/N = N + (x^3/N) We know from discovery that (x^3/N) = (x^2/y) So, we substitute for y in terms of x The simplest substitution is (y=N/x) (For another equation we could substitute: (y=(N^2/x)+x^2/N) Another equation in terms of y is: (y=(N^2/x + x^2)/N). This can also be substitute into (x^3/N) = (x^2/y), and graphed. Look at the graphs on the attached pdf. Do you see it now? GraphicCalcSimple.pdf

N=85 x=5 y=17 All my math problems deal with semiPrimes. Is there a pattern? Does it only work with semiPrimes? Can you reduce the fraction to N/oversomedenominator? Has it been observed before? I did not derive it from an equation directly. I am looking for patterns and thought this was one. But I will share if you deem it interesting.

(x^3/N) approximately= (x^2/y) (25/17) approximately= (85/58) Thoughts?