Trurl

On 4/20/2024 at 11:25 PM, KJW said:

As a result of this thread, I did some exploration of factoring semiprimes. I even came up with a solution of sorts, but this didn't seem to be any more efficient than brute force.

I also wanted to say I’m happy to hear this post encouraged you to research SemiPrimes. That is what it is all about. I was going to be an adult educator until the professor failed me. But that is another story.

I also hope that if you take the inverse of the dozens of equations that it will make the graph better for visual inspection.

I also would be interested in what you are working on. Maybe you will share in the forums someday.

BTW does anyone know what the picture of the writing on the wall is?

You are right about the brute force. I don’t know how useful it is when the smaller factor is occurring close to zero anyway.

But what is given me a glimmer of hope is the first graph of my last post cross the x axis at around 41227. That’s where it appears to cross but computer generated graphics can be deceiving.

If anyone could show where y on the graph equal zero that is the x intercept of that fist graph of the last post, it would be well appreciated.

Ok, I haven’t been here in 3 months. I was walking around and read the writing on the wall. And it made me think I should be working on mechanics instead of such abstract ideas of factoring SemiPrimes.

But my work was not without reward. But of course graphs can appear deceiving. Often graphs show a limited view. (Like in the old days of CAD when you couldn’t revolve the view in 360 degrees. You had to change the angle of the view by typing in coordinates).

The question is, “Is this graph deceiving?”

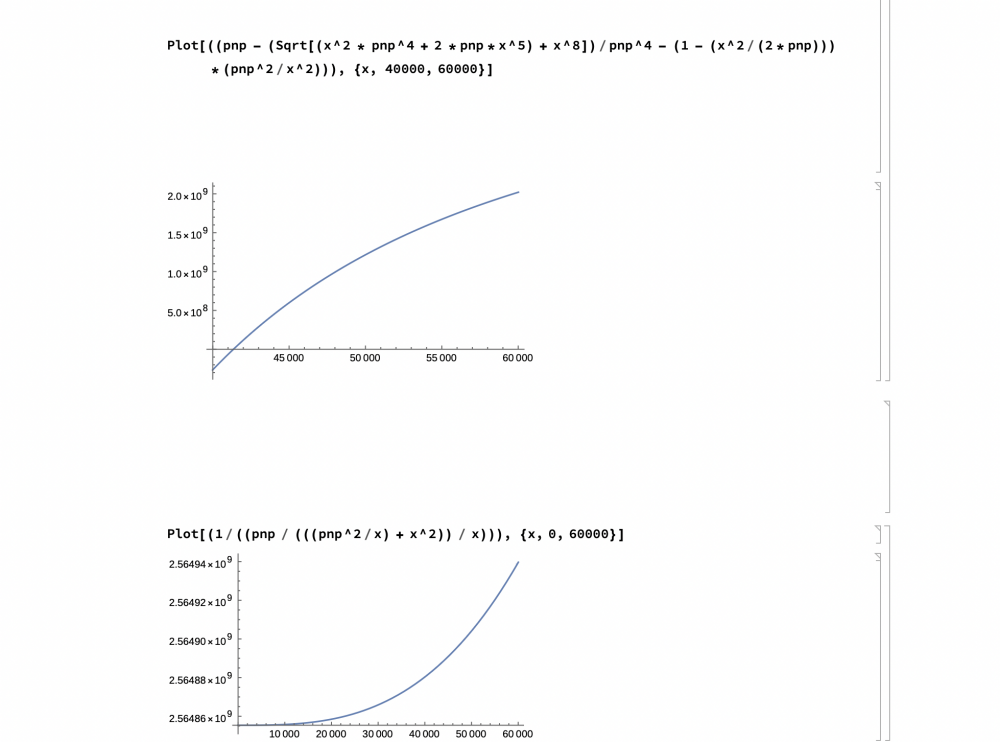
Clear[x, pnp]

pnp = 2564855351

Show[
 
 
 
 
 Plot[(( (((pnp^2/x) + x^2)) / x) /pnp), {x, 0, 60000}]
 
 
 ]










Plot[((pnp - (Sqrt[(x^2 * pnp^4 + 2 *pnp*x^5) + x^8])/
     pnp^4 - (1 - (x^2/(2*pnp))) *(pnp^2/x^2))), {x, 40000, 60000}]










Plot[(1/((pnp / (((pnp^2/x) + x^2)) / x))), {x, 0, 60000}]

This code works!!!!!!!

Working Mathematica Code:

Clear[x,p];



p=2564855351;
x=3;


Monitor[While[x<p, If[(x*(Sqrt[p^3/(p*x^2+x)])-p)<0.5, Print[x];
   Break[];];
  x+=2;];
 If [x <= p, While[x<p, If[Divisible[p,x],
     Print[x];
     Break[];];
    x +=2;];], x]
3
41227

p = 2564855351;
x = 3;
Monitor[While[x <= p, If[(x*(Sqrt[p^3/(p*x^2 + x)]) - p) < 0.5, Print[x];
   Break[];];
  x += 2;

Missing parentheses, but the logic is there.

The language is Mathematica. I collaborated with another Mathematica coder. I’m not familiar with the “Monitor” class.

But this class is the representation of everything I have posted. If it is the syntax I will have to consult more Mathematica coders.

Attention all coders!!!

p = 2564855351;
x = 3;
Monitor[While[x <= p, If[(Sqrt[p^3/(p*x^2 + x)] - p) < 0.5, Print[x];
   Break[];];
  x += 2;];
 If[x <= p, While[x <= p, If[Divisible[p, x], Print[x];
     Break[];];
    x += 2;];], x]

First function corrected:

p = 2564855351;
x = 3;
Monitor[While[x <= p, If[x*(Sqrt[p^3/(p*x^2 + x)]) - p) < 0.5, Print[x];
   Break[];];
  x += 2;

Same as all my recent descriptions.

Well leaving out the x was a happy accident. It just shows again x times y = p and we are just using algebra.

4 hours ago, Ghideon said:

What does "within range" mean?

That is why the second part of the program used division. The first algorithm found where x value of the small factor approached zero value at y. I put the value of y at p minus x times y so it is easier to find.

I could have said x at factor and y equals pnp.

I said within range because there is some error with x. It is close but within error.

4 hours ago, Ghideon said:

What do you mean by "approaches”?

The equation is too complex to solve for x even though it has x as the only unknown. I say approaches because I am plugging in a test value of x to find y. That is why I graphed it.

I know it is not pretty math and is more of a hack. But using test values you know the area of the factors because the further away the y value on the graph is from zero the further away you are from the factor.

p = 2564855351;
x = 3;
Monitor[While[x <= p, If[(Sqrt[p^3/(p*x^2 + x)] - p) < 0.5, Print[x];
   Break[];];
  x += 2;];

Syntax error. Should read:

p = 2564855351;
x = 3;
Monitor[While[x <= p, If[x*(Sqrt[p^3/(p*x^2 + x)]) - p) < 0.5, Print[x];
   Break[];];
  x += 2;];

That is why it wasn’t working. It was y, the second Prime factor. But we would have no way of knowing when y was reached. Multiple y by x to get p. Subtract p and the y of graph equal to zero. That y intercept is where x approaches the value of the smaller Prime factor.

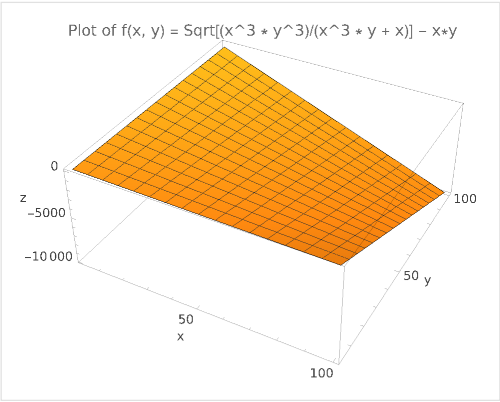
The problem is it is Sqrt[(x^3*pnp^3)/(x^3*pnp+x)-pnp

Where pnp is the constant SemiPrime. 2564855351 in this case

x is the value on the axis. Where y on the graph equals zero, x approaches the smaller SemiPrime.

I believe in your graphs y is variable.

I am working on testing the program. But if you take

p = 2564855351;
x = 3;
Monitor[While[x <= p, If[(Sqrt[p^3/(p*x^2 + x)] - p) < 0.5, Print[x];
   Break[];];
  x += 2;];

and display x when it breaks it should be within range of the smaller Prime factor.

I know testing sounds simple enough but my computers and software are aging. Software upgrades faster than I do. All my software is scattered across 5 computers. And I don’t think Win7 and XP systems are safe on the internet. But that is just my computer maintenance problems. Hope this helps.

There are no  anomalies. When you graph the  equation, the x of the graph (you just graphed) equals the smaller Prime factor where y of the graph is or around zero.

There are no tricks. That is why I called it Simple Yet Interesting.

The code I posted was generated by ChatGPT. It simplified the equation. You should try it in  Mathematica. It is not meant to be efficient but the first function should break (and print) near zero and estimate the smaller factor x.

I have already posted on this.

Let pnp = 2564855351

When x = 41227, the (x*y) part of equation equals 2564855365.5

https://www.scienceforums.net/topic/124453-simple-yet-interesting/page/7/#elControls_1258420_menu

Hope this explains what I was attempting to do. I need to post  another, larger example.

If the program from ChatGPT works you should be able to modify the testing steps ( from every odd number to x+=22 or larger)

The one thing that needs checking is how GPT simplified the equation.

That is why I said test for lager Primes. Because 2 known Primes multiplied together will equal zero in the equation if they form a SemiPrime.

Quote

Finding large primes with your approach unfortunately does not work; mathematical reasons why has been presented already.

@Ghideon

And anyone interested

Yes. I am still dividing and finding a square root in my calculations. How could it be faster than the original recursive division?

Probably not faster, since when you start at 3 the unknown x is closer to zero than pnp anyway.

But the advantage is you don’t need to test those values in my equation that don’t occur next to zero. This zero is unique to pnp. It also occurs in sequential order. So, if you subtract the left side of the equation by pnp and it is, say 5, you know that x is smaller than the tested x at that value.

I know it has many faults, but it does provide a unique graph that may contain some useful analysis.

I think it will prove more useful as pnp increases in value. But it is difficult for me to test. I will try to factor the largest semi-Prime posted earlier. But that is why I posted here in the first place for help testing.

I realize my algorithm isn’t faster than plain division, but that isn’t what it was intended to do. I need outside eyes because I created the algorithm and am biased, but finding semi-Primes is not the only part. Instead, it is to exploit a pattern in factorization.

3x+1 if odd

x/2 if even

So why not create a sieve of multiples of 2, 4, and 8?

When x equals a logarithm of 2, 4, or 8 then x/2 repeated equals 2.

2*2*2*2…

4*4*4*4…

8*8*8*8…

These 3 logarithms of 2, 4, and 8 encompass all the numbers that reduce to 2 when repeatedly divided by 2.

What am I missing? Did I break the rules of the pattern? I am trying real hard not to factor semiPrimes. I did not research the problem yet. I am only working with 3x+1.

I realize that this is more complex with larger numbers. I am just stating a simple example.

@Sensei

@Ghideon

I had help on this program. A good Samaritan put the code into ChatGPT and it supped-up the code.

I still don’t know if it will run faster with larger Primes compared to standard recursive division. I think it gives a picture of what is going on with the factoring. x will only occur around zero on the graph.

Again, I don’t know how to measure any efficiency of the program. Obviously with small Prime products (pnp), it will not show any improvement with factoring the semiprime.

Again, I am breaking a resolution not to enhance RSA. But I wanted to share some final thoughts on this project I have spent great effort on. I think my next project will be Microsoft Kinect or 3D Printing. A friend bought me a book on Nichola Tesla for Christmas. It has his messages. However, the messages are encoded in puzzles and cryptograms. I thought I could write a simple Mathematica program and decode them. If the program works, I will share every detail. Here we go again. LoL. At least it’s not RSA. Even video games would be a good break from RSA.

I know what you are thinking why would I give such information away. That is if you really believe in my program. I know such information is valuable, but if no one attempts to find large Primes with it I don’t know if the program even works. That is why I shared everything in the message board. I have shown my case. Please prove it right by finding large Primes.

p = 2564855351;
x = 3;
Monitor[While[x <= p, If[(Sqrt[p^3/(p*x^2 + x)] - p) < 0.5, Print[x];
   Break[];];
  x += 2;];
 If[x <= p, While[x <= p, If[Divisible[p, x], Print[x];
     Break[];];
    x += 2;];], x]

One of my resolutions this year is to stop trying to enhance RSA cryptography. I have been at it as early as 2006. In my first attempts, I stated that a logarithmic spiral could define a pattern in Prime numbers. I still believe this. And it is inherently feasible because logarithms already explain many patterns.

But my ideas are the same in all my posts: x * y = pnp.

If I had just left the equation at: x * (pnp / x) = pnp ; it wouldn’t have been helpful. I had to find a way to put y terms of x and pnp that was useful and equaled more than 1 =1. The enhanced equation still may be difficult to solve, but with only x as the unknown I could substitute x along the graph and when that value minus pnp approximately equaled zero, the value of x that caused that zero is the smaller Prime factor.

Well despite the fact if you believe me or not Or if this is even useful (I believe it is useful), you could set up an equation similar to this isolating x and testing it along a graph for any pattern. It may be a challenge to put y in terms of x and pnp that only solves the desired pattern, but it would be a shot to analyze the series in ways not done before.

So, as I break or fulfill my resolution, I ask even though it would still be challenging to break RSA with this method, is the method itself useful in trying to find patterns where this is no pattern?

x* y = pnp

x * (Sqrt[ (pnp^3/(pnp * x^2 + x) + (x^4/(pnp^2 + x) )] ) = pnp

x * (Sqrt[ (pnp^3/(pnp * x^2 + x) + (x^4/(pnp^2 + x) )] ) – pnp = 0

Let pnp = 2564855351

When x = 41227, the (x*y) part of equation equals 2564855365.5

Not bad for government work.

Thanks tor the links 😁

One of my New Years resolutions is to stop trying to enhance RSA.

Where is there a list of copyrighted content that is now public? The first Mickey Mouse movie now is public domain.

Also, I thought that all my data analysis on crypto would benefit me in  bioinformatics. Even though I am not a biology major or know much about, I thought I could still work with the statistics.

Is there any online database of open source data to try and crunch and find patterns in genetics?

Quote

13 hours ago, swansont said:

Can you provide those sources

 

The back of the book picture I posted says  it will break RSA, DSA, and ECDSA.

I have yet to read the book, but it proposes alternatives to modern encryption.

The previous link you posted was the first I saw that said today’s encryption was safe.

I have been listening to Michio Kaku’s book. I haven’t finished but he describes quantum computers as pattern solvers. Uses like mapping dna or folding proteins. He doesn’t say we can do that currently. He does mention Google and Microsoft building prototypes.

I guess there is some disagreement on quantum computing. 60 minutes made it sound like it was coming out tomorrow. And there is several sources that say it will break RSA, DSA, and ECDSA.

I’ve heard 40 qubits was the highest. But I believe you that it is far off.

I see quantum computing as producing too much information. We are going to get an answer and it will be so complex that we will have to assume it is correct. I mean something like how you can’t prove a math theory by crunching numbers.

However expanding the amount of different crypto algorithms seems awesome.

BTW, I have not read this book.

Several sources have a cliffhanger: quantum computers defeat modern cryptography.

The book article of chapter 2: The Physics of Quantum Information, Bouwmeester, mainly says the man in the middle attack. If Eve has the public key she can use it to compare her plain text to the cipher text.

The article goes on to say how secure quantum ciphers are. A lot of which I don’t understand.

I still don’t know why modern encryption fails. I will research Shor’s algorithm. Thanks for the tip.

There is currently much interest in A.I. and quantum computers. I am trying to branch out to other subjects than RSA.

But both subjects may destroy humanity. I only say this as a fact of science, but isn’t a device that can manipulate atoms and have infinite processing power God?

Why does the invention of a quantum computer mean the end of RSA?

I have seen many sources that claim this, but they never explain the “how.” The one explanation I have read is that they have one of the keys and the way quantum computers work they reveal the pattern only knowing the given part.

My question is does this only imply to modern key sizes? What would prevent someone from using a quantum computer to make a gigantic semiprime to factor?

And do quantum computers explain mathematical patterns? I don’t think by factoring the RSA semiprimes it would find a pattern. Isn’t the quantum computer still just crunching numbers?

From my reading, it was said that quantum computers will design a custom key system every time. I understood it as being a sort of geometry that unique to all computers.

Combine A.I. and quantum and you have a thinking machine that can manipulate the world through atoms. SFN will now be moderated by the quantum. But that is ok because we can’t keep track of the trillion-digit keys or us finding patterns is no longer needed. Worse yet, we have lost the argument that the world is a simulation. 

I think the scientist’s view determines rather he proves if God does or does not exist to himself.

Before the 20th century science and religion were on the same page. Scientists were only explaining what God created for us.

Some scientists see the work of God in a mathematical series. Other scientists need more evidence. In fact they dedicate their lives to it. Why do we want more knowledge and discoveries? It is to create and unlock mysteries. But for what reason are we doing this? Technology doesn’t always equal improvement. And what are we doing with all this knowledge? Finding better ways to kill each other?

Whatever you believe is a personal choice. Science can’t answer such questions. That is why we seek God.

I realize that I didn’t use an official tax system. I just wanted to illustrate that tax compounded makes more for the government than the amount of money they tax.

I choose sales tax. In high school we are taught this is the most fair tax. The more you spend the more your tax. And everyone pays the same rate. But like most taxes I think the more money you have the less the tax affects you.

But imagine a flea market with dealers buying from one another. Each spends $100 on an item from the other dealer and pays $6 tax on every $100. The $6 is additive. You still need $100 to purchase, but you must add the $6 tax. The tax is subtracted from the individual buyer each time they spend. The $100 is constant.

I am trying to illustrate that the tax has the potential to generate more tax than the original payment of goods. I don’t think this is new. I think it is inherent in taxes themselves.

I would say the inability for governments to track transactions of cryptocurrency is why they want cryptocurrency to fail.

I know if you have tax it takes away from the amount of money you have left. But money transfers it is never destroyed. I am not an economics expert, but somewhere somehow someone has mapped the movement of money between taxpayers and the amount of tax revenue generated.

It isn’t a tax system. I am just raising the question is taxing money making more revenue.

I used sales tax as an example. With every purchase or transaction there is 6%. The cost is $100 to purchase each time. So one person buys something for $100 and pays $6 sales tax. The person who receives the money makes their own purchase of $100 and so forth.

So the same $100 generates revenue more than its original value over time. More transactions means more $6 in tax fees.

Sales tax Pyramid Scheme

Ok say I buy something for$100 + $6.00 sales tax. Then the person I bought from buys something for $100 + $6.00 sales tax. And so on and so forth for n, the number of money transactions.

Does that mean that on $100 the government just make $6.00 * n. And after $100 / $6 times the government is making more money than the original $100?

So the act of saying $100 is worth so much in gold, actually makes more than the value of the gold? And then transfer of money is promoted because it generates more value?

And you thought bitcoin was a scam.

p=2564855351 

For[i = 3, i <= p, i+2,
If[(Sqrt[p^3/(p*i^2+i)] - p) < 0.5,
x = i,
Print[i],
i=p+1
]
]
While[x<=  p, x+2

If[ Divisible[p,x],
Print[x],
p = 1];
]

This was an attempt to target the range of divisors into the semi-Prime. I know I am doing division in the second loop, but the range is smaller, where the test equation of the first loop equals approximately zero.

I know you can argue the usefulness. However, I still argue that at large semi-Primes with this algorithm, the number of test values is significantly less.

And a shout-out to Chat gpt. The reason I am a terrible programmer is syntax; too many languages; too many unknown classes. Now that I have uploaded my algorithm, gpt will render all public key encryption invalid 😜--- only kidding of course. No one believes my work anyway. That was until gpt …