JVNY

I agree that it is tough, but that is part of what makes it interesting. The light emitter and the photographic film that recorded the fringe shift were fixed on Sagnac's rotating disk, so what he recorded was from the POV of the rotating disk, not the inertial frame attached to the center. Trying to understand the effect from the POV of the disk is worthy of effort. And I agree, the c+v and c-v refer to closing speeds. If the observers on the rim try to synchronize their clocks using the Einstein convention sending signals in one direction, then yes I think that each clock is ahead of the one behind it (or vice versa, if the signal were sent in the other direction). I don't know, however, what is simultaneous with what if you synchronize clocks with any given convention (a light signal from the center, or some other method). I am not sure what simultaneity convention properly applies to a rotating rim. So I was focusing first on the explanation of the Sagnac effect; if the closing speeds of the signals measured on the disk relative to their source (on the disk) are the same as the closing speeds of the signals in the lab frame relative to their source (on the disk), i.e. c+v or c-v, that might give some information to help with the subsequent question of simultaneity. But it seems as if the closing speeds are different on the disk.

A couple of thoughts. First, I think that even on the rim (not just in the lab) each clock will tick at the same rate. Say the interior of the rim is mirrored, so that a light signal can travel around the interior. If a clock sends a series of signals around the ring (in either direction), one every second of its proper time, then each other clock on the rim should receive the signals one every second of its proper time (after the initial delay for the first signal of the series to arrive). Second, you are on to something with the simultaneity shift suggestion -- some analyze the Sagnac effect as a shift in simultaneity, like this: http://www.physicsinsights.org/sagnac_1.html However, I don't think that the shift in simultaneity view follows the c+v and c-v analysis of how light travels on the rim (to a rim observer), because the Sagnac effect is the same in absolute value for both the counter- and co-rotating signal (plus or minus 207.4 ns for a signal sent around the earth per the Ashby article linked above). It is definitely worth thinking through.

I am trying to get at the point of view of the rim, not the axis. If a rim is rotating in an inertial laboratory, it makes sense that signals sent in opposite directions around the rim travel in the lab frame relative to their starting point on the rim at c+v or c-v. However, the result of +v or -v applying is that the difference in lab time between the arrival of counter- and co-rotating signals back at their starting point on the rim will depend on the speed of the signals. On the rim, however, the difference in arrival times does not depend on the speed of the signals. Any pair of opposite signals sent around the rim (light flashes, slow traveling portable clocks, etc.) will have the same difference in arrival time due to the Sagnac effect as measured by an observer fixed on the rotating rim. See, for example, Ashby and Allan on slow clocks carried around the earth (http://tf.nist.gov/timefreq/general/pdf/133.pdf , page 652), and Ashby on clocks around the earth that are synchronized using the Einstein convention with light signals sent around the earth (http://areeweb.polito.it/ricerca/relgrav/solciclos/ashby_d.pdf , page 15) (excerpts attached). Because the difference in arrival time as measured on the rim (by an emitter and receptor fixed on the rim) does not depend on signal velocity, it cannot be right to explain the Sagnac effect as being due to light traveling at c+v or c-v as measured by a rim observer. The standard explanation seems to confuse what is happening in the inertial laboratory frame with what is happening on the rim itself.

I suspect that you can do this. You might not even need more than one section. Say that you have (1) a stationary, hollow cylinder with its inside surface mirrored, and (2) a single light emitter/light receiver unit. You set the unit into motion circling around the interior of the cylinder like a motorcycle in the classic "wall of death" carnival sideshow, see http://en.wikipedia.org/wiki/Wall_of_death_(carnival_sideshow). Then the unit sends a flash of light in each direction. I suspect that the same result would occur (the unit would record a fringe shift for the returning flashes when they arrive at the unit). Dufour and Prunier ran the Sagnac experiment with different parts of the device fixed in the lab rather than on the disk (such as fixing some of the mirrors in the lab), and their experiments got the same approximate fringe shift results as the one with all parts fixed on the disk. See http://www.conspiracyoflight.com/pdf/Dufour_and_Prunier-On_the_Fringe_Movement_Registered_on_a_Platform_in_Uniform_Motion_(1942).pdf

Makes sense, thanks.

Thanks to both swansont and phyti. The thing that confuses me about the particular quotation is the phrase "the sum and difference of the speed of light and the speed of some other object, both with respect to a single inertial coordinate system . . ." Given that the emitter and detector are both on the disk, the result (fringe shift recorded on film) has nothing to do with any inertial coordinate system. If you set the interferometer into translational movement rather than rotation, the film will not record any fringe shift (swansont: "you get a fringe shift in a rotating Sagnac interferometer but not in a translating one"). It is only in another inertial coordinate system (say a laboratory relative to which the interferometer is moving) that one would observe light to move relative to the interferometer at c plus or minus v. Given that the entire experiment (including the photographing of the fringe shift) occurs on the disk, which is not inertial, utilizing the concept of "a single inertial coordinate system" seems irrelevant and confusing.

Here is a typical explanation of the Sagnac effect: Clearly the pulse traveling in the same direction as the rotation of the loop must travel a slightly greater distance than the pulse traveling in the opposite direction, due to the angular displacement of the loop during the transit. . . [T]he expressions "c+v" and "c-v" appearing in the derivation of the phase shift . . . do not refer to the speed of light, but rather to the sum and difference of the speed of light and the speed of some other object, both with respect to a single inertial coordinate system, which can be as great as 2c according to special relativity . . . http://mathpages.com/rr/s2-07/2-07.htm I am having difficulty grasping this explanation because all parts of the interferometer in the classic Sagnac experiment are fixed on the rotating disk (including both the light source and the film that receives and records the light waves). So the experiment does not seem to measure light speed plus or minus rotational speed with respect to some inertial coordinate system (such as the lab system in which the disk rotates). The experiment seems to measure light speed entirely with respect to points on the disk. Can anyone offer suggestions about how to interpret or supplement this explanation? Thanks.

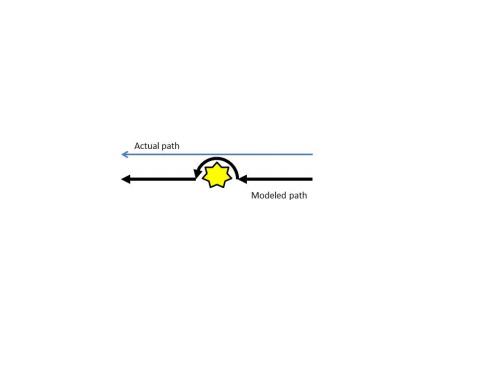
I think that they even state that the line for the actual path is straight (no aberration) because the aberration is so small that it cannot be represented in the simple drawing.

It is essentially their drawing (without copying it outright and violating any copyright they might have in it). But remember that they expressly state that they are modeling a different path than the actual experiment, in order to simplify the math. They acknowledge that their answer is therefore only an approximation of the actual experiment. Their method yields 250 microseconds; xyzt recalls that the actual is around 200 microseconds. So it is clearly only an approximation.

Sure. Although I do not understand them, I can post them for you. For radial path segments they use: dr/dt = 1 - (2M / r) [note that for c=1, I believe that this is the same as your post 3 formula: ] and then integrate: dt = dr / (1 - (2M / r)) They define r as the "coordinate" radius (or reduced circumference, or r-coordinate) and say that it is called a radius "despite its being no true radius" (page 2-9). They use an approximation for 2M/r: (1 + d)^n = 1 + nd And from this they get 53 microseconds delay for the radial segment Earth to Sun. Then, for tangential semicircular path they use: ds/dt = (1 - (2M / r))^(1/2) They assume that r = R for the entire semicircle, so they solve that equation for dt and sum it along the entire semicircular path of length πR, being: πR / (1 - (2M /r))^(1/2) And they use the approximation again and get a delay of approximately 15 microseconds. They don't do the Sun to Mars segment in detail, but they instruct the reader to use rMorbit = 2.28 E +11 meters, and they say that this generates a time delay for that segment of 57 microseconds. So their total time delay is 53 + 15 + 57 = 125 microseconds each way, or 250 microseconds for the round trip. The chapter on the time delay is a "project," so Taylor and Wheeler do not show each step of their calculation. They show what I posted, generally saying to the reader to use certain formulas and then ask the reader to show that the results are the numbers above.

It seems that the biggest issues are (1) whether slower coordinate speed of light has any physical meaning, (2) if one believes so whether one is mainstream or fringe, and (3) whether the coordinate speed of light (the speed as measured by a distant observer) is a valid explanation of the Shapiro delay. Taylor and Wheeler are certainly mainstream, and here are excerpts from their book "Exploring Black Holes: Introduction to General Relativity." The text answers the questions (1) yes, (2) mainstream, and (3) yes. Project (i.e., chapter) E is titled "Light Slowed Near Sun." That pretty much answers all of the questions implicitly from the start. Here goes with excerpts. The text sets forth the initial questions: * What happened to "Light always moves with the same speed"? * Who says light slows down near Sun? * How much does light slow down near Sun? * Does observation verify the predicted value of the slow-down? [from page facing E-1] The Schwarzschild bookkeeper records a "smaller speed of light" than do . . . free-float observers . . . That is the prediction of our analysis . . . Does this prediction have a physical meaning at all? Is there any way to measure this "slowing down of the speed of light" as reckoned by remote observers? "Yes" and "yes" were the answers predicted by Irwin Shapiro and demonstrated by him and coworkers. [from page E-1] So, Taylor and Wheeler literally ask the question whether the slower speed of light as reckoned by remote observers has a physical meaning, and they state that Shapiro answers "yes" it does. Question (1) above is answered "yes." This answer comes from Shapiro himself (according to Taylor and Wheeler) and it is included in Taylor and Wheeler's book, so it seems pretty mainstream. Question (2) above is answered "mainstream." Taylor and Wheeler then analyze the Shapiro delay. They state that it is too awkward to integrate the equation for the "skimming" path of light next to Sun that the Shapiro experiments actually use [page E-2]. So they state that: Instead we obtain an estimate of the delay time by assuming a slightly different path . . . that comes in radially from Earth, circles halfway around Sun in a tangential semicircular path, then moves out radially . . . This alternative path . . . yields an estimate much closer to a precise calculation than we might have expected. [page E-2] They use an illustration like the attached. They then calculate the delay as a combination of the radial and semicircular segments. The calculation uses the radial Shapiro delay formula, as does Iggy. Taylor and Wheeler's slightly different path generates a delay very close to the actual delay determined by experiments (approximately 250 ms modeled delay for a roundtrip to Mars). This is a delay "reckoned by remote observers" [per Taylor and Wheeler, page E-1], so it is in fact the coordinate speed of light measured by distant observers [as phrased by xyzt]. So, the coordinate speed of light is the valid explanation of the Shapiro delay. The answer to question (3) above is "yes." Going back to Taylor and Wheeler's introductory questions to the project, and answering them: * What happened to "Light always moves with the same speed"? [light travels slower near gravity as measured by distant observers, which has real physical meaning] * Who says light slows down near Sun? [shapiro, for one, according to Taylor and Wheeler] * How much does light slow down near Sun? [approximately 250 ms for the Earth-Mars round trip] * Does observation verify the predicted value of the slow-down? [yes]

I agree with this. What I did in the other exercises was to proportionately adjust all of the clocks' tick rates to the same rate (the farther rearward, the more elapsed ticks show on the clock than actual ticks of time for that rocket's clock). I think that you would call this putting all of the clocks on the same coordinate time. That eliminates the time dilation effect. It leaves only the distance effect. If you calculate the speed of light using the proper distance, then you get the speed of light slowing the closer the rocket is to the rear of the accelerating row (or the deeper in a gravitational well). I think that xyzt objects to that description: Having heard from a lot of members who have been kind enough to respond, and done a lot of reading, I think that it is reasonable to consider two descriptions to be true. First, the speed of light is constant. In gravity, the distance that one is measuring when doing a Shapiro delay experiment is greater when the sun is between the earth and the other planet than when the the sun is not. The greater time that the experimenter on earth measures in the former case is due to the fact that the distance is greater. Second, in the earth experimenter's frame the speed of light is not constant; the speed slows when the sun is between the earth and the other planet. Call this the coordinate speed of light; that is fine. But it is not "devoid of any physical meaning." It is measurable by the earth experimenter. We cannot simply change our coordinates to get another value -- we live on earth, we send signals out into space, and we need to take this effect into account when doing calculations that depend on the amount of our proper time that passes before the signals return (or before the signals reach a spacecraft that we have sent into space). Here is an excellent example of the two views, both from the same person. Neil Ashby is responsible for the GR corrections in the GPS system: http://en.wikipedia.org/wiki/Neil_Ashby Here is a piece that he coauthored about GPS corrections: http://www.gps.gov/cgsic/meetings/2012/weiss2.pdf This notes that there are relativity terms that are becoming important in the GPS system. Slide 2 describes two effects that are not currently used in the GPS corrections: "Signal Propagation Delay" caused by "Earth's Gravitational Field." The first of the two is expressly called the Shapiro delay on slide 15. So, one way of looking at the effect is that gravity causes signal propagation delay, which I think can fairly be interpreted only one way -- that gravity slows down the signal (delaying something is slowing it). If we want to make the GPS system more precise, we would need to correct for this signal delay. It has physical meaning; we live on the earth, drive our cars here, shoot guided missiles at each other here, etc. So we cannot deny the physical reality or importance of this signal slowing. On the other hand, Ashby also says (from the other perspective) that the effect is one of greater distance: the distance is the coordinate distance plus the "so-called" Shapiro delay (slide 3). So it seems to be fair to view the question from both perspectives, at least if you want to be able to both understand GR and build an accurate GPS system.

I get the same, thanks, and I apologize for getting the question numbering wrong (and for stipulating that the ships accelerate at 0 rather than 60 in their frame, making it a bit awkward). I will put together a Minkowski diagram shortly and think about your question about the time it takes for the ship to pass, but here is a summary and finishing off of question 5. The ships initially present 80 apart in the ground frame, with their clocks not synchronized there. The rear (Bert) clock is ahead by the product of velocity and proper length, hence 100 * 0.6 = 60. Events that are simultaneous in the Bert/Frank frame (like clock striking 60) are not simultaneous in the ground frame. Events at the rear happen 60 units of Bert/Frank time earlier in the ground frame than events at the front. So Frank's clock reads 0 and Bert's 60 in the ground frame. Now let's assume simultaneous acceleration in the Bert/Frank frame at their time 60 (since Bert is already at 60, and we don't want to have to go back in time . . .). Bert accelerates first in the ground frame (his clock reads 60 at inception). It takes 60 units of Frank time, with Frank traveling at 0.6, before Frank accelerates. That is a head start in the ground frame for Bert of 75 units of ground time, so Bert closes 15 of the separation in the ground frame as you calculated, leading to a 65 distance in the ground frame when Frank accelerates (thus ending Bert's head start and locking in the 65 ground distance). During Bert's head start, he is traveling at 0.8, so his clock ticks slower in the ground frame than Frank's. As you note, Bert's clock ticks only 45 while Frank's ticks 60. The new gamma for Bert is 1.667 (because he is traveling at 0.8), and 75 ground time / 1.667 = 45. Thus, at the time Frank accelerates, Bert's clock reads 105 in the ground frame (60 at the start, plus 45). Frank's reads 60. The difference in clock times in the ground frame is 45 as you note. The proper distance between the ships is the ground distance times gamma, or 65 * 1.667 = 108.333. Both ships are at rest with respect to each other (in the same reference frame). If the clocks are still synchronized in their frame, then Bert's should be ahead of Frank's in the ground frame by the product of proper distance and velocity, or 108.333 * 0.8 = 86.667. But it is only ahead by 45. So Bert's clock has fallen behind in their frame. So, the example shows that: Ships that accelerate at the same rate cannot maintain their proper distance. The proper distance increased by 8.333 in the example. The front ship has to accelerate at a lower rate to maintain proper distance. If the two ships accelerate Born rigidly, then they will maintain their proper distance at all times. Consistent with another post above, same proper distance at all times = at rest with respect to each other at all times = in the same reference frame as each other at all times = agree on simultaneity with each other at all times. Their clocks will run at different rates in their own frame, admittedly. As the example shows, the rear clock actually runs at a slower rate in the ships' frame (thinking about this leads to the equivalence principle, with Bert being lower in the gravity well than Frank). But if they accelerate Born rigidly, with Frank accelerating at a lower rate than Bert, they can maintain their proper distance, stay at rest with respect to each other, remain in a common reference frame, and as a result agree on the simultaneity of events.

Getting back to the initial posts, I will go out on a limb and say that yknot is not nuts. There are three events: (1) emission of light, (2) light striking O1, and (3) light striking O2. The light emission and the light strikes are all events, and serious physicists would agree. Witness Taylor and Wheeler, Spacetime Physics, page 10: "Another event is the emission of a flash of light from an atom . . . A fourth event . . . is the strike of a lightning bolt on the rudder of an airplane." See also the (less august) wikipedia entry on "Spacetime": "Events which occur to . . . a photon along its path (i.e., while traveling at c, the speed of light), all have light-like separations." yknot correctly described the events that occur to the photons (striking the observers) as events, and correctly described them as being light-like events (perhaps better to say, like wikipedia, that they have light-like separation). Also, it is not necessary to have a second light source to show the relativity of simultaneity (although Einstein uses one in the train example, and admittedly yknot is using the train example). All you need is a light source that flashes spherically outward. Then, when the light strikes observers who are equidistant and on opposite sides of the light source in its frame, the strikes will be simultaneous in the light source's frame. But they will not be simultaneous in other frames that are in motion relative to that frame. See Spacetime Physics at page 176. yknot, in your original post you say that the two strikes are absolutely in the order O1 first and O2 second because they are light-like. But it is not the case that all events that have light-like separation occur the same order in all inertial reference frames, as Taylor and Wheeler show. I agree with the early responses that the relative motion is important, and that it is fundamentally what special relativity is all about. If you use a second light source on the opposite side of the observers, or if you separate the two observers slightly at inception and put the light source between them, there will still be differences in how the observers observe the light (just as you point out in your original post), but as the other posters say this just illustrates special relativity. It is not inconsistent with SR.

This site says 20% of all humans who ever lived past age 65 are alive today: http://www.trinity.edu/mkearl/ger-biol.html So I suspect you have to go a lot higher than age 50, perhaps age 90 or 100.