Posts posted by ydoaPs
-
-
It depends on the kind of classical physics and the complexity. If you want to understand basic toy kinematics and dynamics at the high school level, you could get away with going up to the first order differential equations.
You'll be doing stuff like taking the derivative of a displacement equation to get a velocity equation.
If you want to understand more complex problems with more modern paradigms, then you'll need multivariable calculus.
You'll be doing things like solving the Euler-Lagrange equations and integrating Lagrangians to find the least action.
With waves, electromagnetism, and "Modern Physics", that table of contents specifically tells me you'll likely need the multivariable parts of the calculus text as well.
But it might be simplified for like an introductory course. You'll have to look at the physics book. If it has [math]\partial[/math] or an upside-down triangle,you know you'll need the multivariable parts.
TL;DR:
That physics book's topics suggest you'll need the entirety of the calculus book
Edit:
!Moderator Note
Topic moved from Lounge to Classical Physics
-
On 9/29/2021 at 6:14 PM, swansont said:
You have an infinite number of points in any finite, one-dimensional line segment. So this is incorrect.
It should be pointed out that this is an uncountabe infinity. It is waaaaaaaaaaaaaaay bigger than the infinite cardinality of the natural numbers
Infinities come in different sizes
-
-
On 5/9/2021 at 11:04 PM, neonwarrior said:
Hello everyone,
Why -2 .(-3) = 6
Why is it positive?
Why we accept that (minus sign) times (minus sign) is positive ? What is its origin?
Thanks in advance
It's good that you asked in Linear Algebra And Group Theory, because we're going to need some algebra you likely have never seen (unless you went to college) to answer it.
Multiplication isn't one thing. What multiplication is depends on what you're multiplying. Algebra is how we define this.
In Algebra, there are a handful of different kinds of structures. Here, we're interested in Groups, Rings, and Fields. Rings and Fields are kind of made of Groups, so we'll start there.
Say we have a set (the lay concept of set will work fine for our purposes), and we'll call it S.
On this set, we need to define a rule called a "binary relation" that takes any two things in the set and gives some output. We want this set to be closed under this relation, so the relation can only give us things that are already in the set. For this combination of set and relation (for now, we'll use ? to denote the relation) to be a Group, they need to have the following properties:
1) Associativity: for any three things a, b, and c in the set, the relation doesn't care about where the parentheses go. a?(b?c)=(a?b)?c
2) Identity: there is a special thing in the set (traditionally denoted by e when talking abstractly) where, for any other thing a in the set, a?e=e?a=a
3) Invertability: for any thing a in the set, there is another thing in the set a* where a?a*=e=a*
That's enough to be a Group. But we want a special kind of Group, called an Abelian Group. That's just a regular Group that has an extra property:
4) Commutativity: for any two things a and b in the set, a?b=b?a
Tradition dictates that for Abelian Groups, + is used in place of ? and 0 is used in place of e and -a in place of a*. If a Group is not Abelian, we often use × (or nothing at all) in place of ? and 1 in place of e and 1/a in place of a*.
If S is the set, we write (S, +) or (S, ×) for the group, but we often just write S if it is clear from the context that we're talking about a group.
This is enough to let us build a Ring.
With Rings, we still have a set S, but we have two relations. (S, +) is an Abelian Group, but × is a bit more lax. × only has to satisfy two properties:
1) Identity, and
2) Distributivity: for any three things a, b, and c in S, a×(b+c)=(a×b)+(a×c)
Like how (S, ?) is a Group, (S, +, ×) is a Ring.
If a Ring is commutative and has inverses for each relation, then the Ring is called a Field.
There are four particularly important facts mentioned above that are important to why a negative times a negative is a positive:
1) a+(-a)=0,
2) a+0=a,
3) a×0=0 (not mentioned above, but still important), and
4) a×(b+c)=(a×b)+(a×c)
Proof -a×-b = a×b:
Let a and b be positive numbers in our field (S, +, ×).
0=b+(-b)=a(b+(-b))
-a×-b = (-a×-b) + a(b+(-b)) = -a×-b + a×b + a×-b = -a×-b + a×-b + a×b = -b×a + -b×-a +a×b = -b(a+(-a)) + a×b = a×b
TL;DR:
It's because Fields are commutative, have identities, and are distributive
-
On 12/15/2019 at 8:34 PM, NonScientist said:
Okay, so I’m new here. Hi everyone.
So I’m not sure why this is affecting me this severely, but I recently discovered the whole “free will vs. determinism” question, and I’ve realized quickly that I should’ve never been introduced to this idea, because I’m finding it almost impossible to deal with the notion of not having free will. It has sent my mind into this state of extreme shock, agony, and despair that almost seems insurmountable. It’s like my whole world and everything I believed has been flipped on its head. I’m serious in saying that this has sent me into a straight panic and shock. I feel like I’m having this nervous breakdown. It’s an overwhelming feeling.
I’m trying to keep myself calm and just relax, but this has really messed me up.
Does anyone here believe in free will? Or can offer any good defenses or arguments for free will? I feel like I need to be reassured that there is free will or else I won’t be able to deal with it. The idea that everything is predetermined, and I’m just robot with no agency or ability to do otherwise is more than my psyche can handle. I’m sort of in this crisis.
How many coin flips does it take to make a free choice?
-
-
-
-
-
Hello ydoaPs,
Layer logic is more similar to (a modified) classical propositional logic than to modal logic.
It does not handle modalities or possibilities.
It uses three truth values „true“, „false“ and „undefined“.
The most important feature are the layers.
A propostion in layer logic does not have one truth value but has a truth value in every layer 0,1,2,3,... ,
and different truth values in different layers are allowed.
So in a way every proposition has an infinite truth vector.
The layers are like additional new dimensions and allow new handlings of contradictions.
Yours
Trestone
If there's no relating the layers to each other, what's the point? If there is, then it's just modality with another name.
-
-
Learn some math. Even the really basic stuff can let you do really cool things. Many of the machine learning techniques aren't all that mathematically complicated. Neural networks, for examples, are little more than optimizing weighted averages of a step (or sigmoid or something like a sigmoid) function.
-
Make your comments descriptive and useful (e.g. don't comment a line that increments a counter with /* increment counter */, try something like /* keep track of the number of lines we have processed */). Imagine you are explaining your code to someone else (who isn't as smart as you) when writing comments.
Add comments at the start of each file saying what that file contains.
Add comments at the start of each function/procedure saying what the function does, what parameters it takes and what it returns. Add comments at each step in the function explaining what it is doing and why it is doing it that way - it is OK to document your design decisions in the comments. Otherwise, one day you might come back and think, "that seems an odd way of doing it; I think I'll simplify it .... Oh no! Why doesn't it work any more!?"
As well as using meaningful variable names, add comments to the declarations with more info (e.g. why it is that type /* We use a set rather than a list here to automatically remove duplicates, and we don't care about the ordering */)
If you "temporarily" comment out lines to try a different implementation then:
1. Add a comment explaining why those lines are commented out
2. Consider deleting them when you are happy with the new version
3. Start using a version control system!
Keep the comments up to date with the code; e.g. if a function is given an extra parameter, update the comments.
A common analogy is to comment like you're explaining it to a rubber duck.
-
I noticed that a lot of the programming questions here, while phrased in terms of coding in specific languages, are actually rooted in a broader context of programming itself. People are having problem with the ideas behind programming in general. If we help people with algorithm building, the language-specific syntax falls into place.
So, this thread is for tips on programming in general. This isn't about programming in python or programming in java. This is about the fundamental heart of what one needs to do. If anything, it's tips on how to code in PseudocodeTM.
I'll start:
One of the biggest thing about programming is being able to break a problem down into chunks and then break those subproblems down. Keep doing that until you get a picture of what specifically you need to do to accomplish each major step. So, if your program needs to do things in three big steps, start even lower than pseudocode; start with a list.
Step 1
Step 2
Step 3
Then, take each of those steps and do the same thing.
Step 1:
Step 1a
Step 1b
Step 1c
Step 2:Step 2a
Step 2b
Step 2c
Step 3:Step 3a
Step 3b
Step 3c
You may or may not notice the indentation. That brings up my second tip.
Use indentation, called "whitespace", in your programs and even pseudocode. Some languages require you to have whitespace indentation (like python and the never ending tabs v spaces war), but many do not. It is still good practice for writing though. Most languages have interpreters or compilers that ignore anything about whitespace other than whether there is at least one space between two letters, so it won't hurt the program but it will help you. Writing, or at least planning, with whitespace keeps ideas organized. Look at the example in the previous tip. You see each substep, and it's clear where in the logic that it belongs. It makes code easier to read and understand, even if it's not required.
Speaking of readability and understanding, that's where my last two tips come in.
Make good names. Names like "MyFunction" or MY_CONSTANT are bad names. They don't tell you what the function is doing or what the constant is for. Make names descriptive, and your code will be easier to understand and easier to read. Rename (or "refactor") if you need to. Many programming environments will even let you replace all instances of one name with instances of the new name, so it won't even be a long tedious thing. Renaming, if giving a new name, is a good thing. It promotes clarity.
Comment everywhere. Comment to the point that you think you're overcommenting, and then comment some more. Future you will likely have no idea what your code is doing, so leave good notes for future you to use to figure it out.
Your turn.
-
-
It isn't paradoxical the answer is that once the host opens the first door with a goat behind it you have a 50:50 chance of getting the car.
That's the incorrect answer. You can do it just marking out the possibility space with pictures of doors, cars, and goats, or you can do it the Bayesian way and you get the same answer. That answer is not 50/50.
You can run actual trials (as Mythbusters did) and confirm. 50/50 is an incorrect answer.
Horrible quality video to follow:
-
-
-
-
-
fiveworlds is taking a week long vacation after plagiarism and publicly posting PMs without permission.
-
HRamjetTesla has been banned at his own request and for an abusive meltdown.
And Soral has been banned as a sockpuppet of Frank_Baker.
-
-

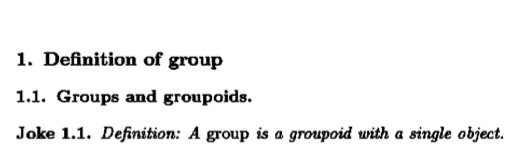
How big is a point? (Can be that the Natural Numbers are Finite?)
in Linear Algebra and Group Theory
When you're talking about volumes and hypervolumes, your set needs to be equipped with a measure function. The technicalities are too much to go into in a single post, but see the wiki link if you're interested.
The standard measure used on the Reals is the Lebesgue measure where the length (in one dimension) is just the difference of the endpoints.
So, if we're looking at the length of a point p, we need to just take p-p, which is, of course, 0.