Everything posted by Jacek
-
Physical, conformal age of the universe
Like I'm the one who cares about your sympathy... You apparently also DGAF (your choice of words - how civil) about on topic discussion, since you don't answer my questions regarding your statements. And you moved my thread from Astronomy and Cosmology to Speculations after 2 weeks and after my question and answer, what would be aging in the expanding universe without matter. And you still don't have your own answer to this question.
-
Physical, conformal age of the universe
Wrong assumption. Also, asking on-topic questions for @swansont is all I'm doing at the moment if you look above. As for you, you must be proud of this bold red font of yours, aren't you?
-
Physical, conformal age of the universe
Was there non-smooth drop or increase in the radiation temperature, caused by recombination and the emission of CMB? I was asking about the temperature of radiation before recombination. I think you still owe me moving this thread to your trash, don't you? Yes, our attitude is off-putting. I'm not kind to you, because you're a part of cancel culture for me.
-
Physical, conformal age of the universe
@exchemist ask @swansont
-
Physical, conformal age of the universe
Part of my homework should be yours, because you were asking me about the radiation before the CMB emission and I answered accordingly to my knowledge. Then you wrote about the reset of the thermal distribution by this emission, so I thought you should know basic parameter of this distribution. Are you saying that both the radiation right before recombination and hydrogen atoms at the moment of recombination were at 3000K? If that's the case, it wasn't reset.
-
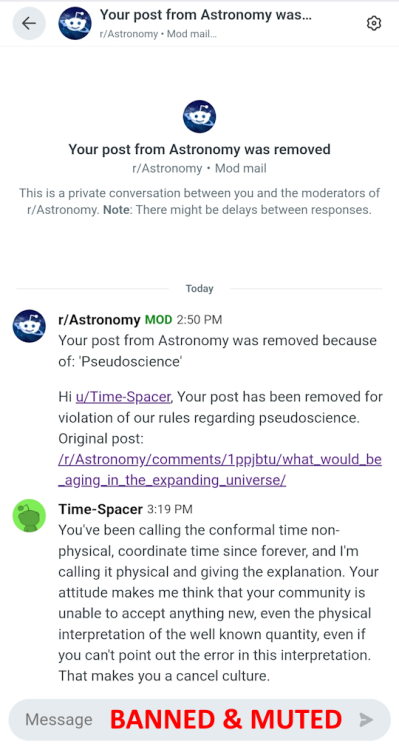
Cancel culture in major astronomy communities
Do you really think that deleting my post, muting and banning me adds to the credibility of astronomy forums?
-
Physical, conformal age of the universe
@swansont Our on-topic discussion had stopped on the temperature of hydrogen at the moment of recombination. Can you tell the radiation and matter energy densities right before and right after recombination? I'm also interested in the temperature of radiation right before recombination.
-
The real freedom
Sorry, I can't help myself :) https://youtu.be/lLCEUpIg8rE
-
Cancel culture in major astronomy communities
That's just the latest example. And that's my pseudoscience on this forum: https://www.scienceforums.net/topic/140204-physical-conformal-age-of-the-universe/#findComment-1305214
-
Physical, conformal age of the universe
I did my best. I can see that's not enough for you, but I also think it would never be.
-
Physical, conformal age of the universe
On-topic: How would you answer my question from this post: https://www.scienceforums.net/topic/140204-physical-conformal-age-of-the-universe/#findComment-1305214?
-
Physical, conformal age of the universe
-
Physical, conformal age of the universe
It's nice to be kept out of your trash, thank you. How would you answer my question from this post: https://www.scienceforums.net/topic/140204-physical-conformal-age-of-the-universe/#findComment-1305214?
-
Physical, conformal age of the universe
Yes, I am. Are you able to admit that it's not pseudoscientific?
-
Physical, conformal age of the universe
@swansont @Phi for All @CharonY @Dave @Cap'n Refsmmat No maths / Incomprehensible / You are contradicting accepted science / No evidence / No physical basis / Obvious errors / It's not science - Which is it in my case?
-
Physical, conformal age of the universe
What would be aging in the expanding universe without matter? How can you tell the age of such a universe without assuming the world line of the material observer? How would you calculate it? Below is more elaborate version of my previous post and my own answer to the title question. SI definition of a second: "The duration of 9 192 631 770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium-133 atom." If we give the cosmic time (equal to the universe age equal to the proper time of the observer resting in the CMB reference frame) in seconds, we can easily give it in the number of radiation periods from SI definition of a second. In the same manner we can define a physical, conformal age of the universe. That's the duration of a certain number of the extending CMB radiation periods proportional to the extending peak wavelength of this radiation that passed through a point at which the CMB is isotropic, since its emission. Proportionality factor is the speed of light, because c=λ/T where λ is the extending peak wavelength, and T is the extending wave period. Conformal time η=∫dη=∫dt/a(t)=47Gy is the conformal age of the universe and I don't question it. I'm proposing a physical definition for it. The inverse of the scale factor 1/a(t) is increasing with time counted backwards, because 0<a(t)≤1 and a(t₀)=1, where t₀ is the present, proper age of the universe. That makes dt/a(t)=(z(t)+1)dt the equivalent of the wave period extending over time counted backwards. We're integrating over it to sum it up. The observed redshift z(t) of light emitted at the past time t and increased by 1 is equal to the expansion of the wavelength, period and the universe itself. Astronomy has been calling it non-physical, coordinate time since forever. I'm calling it physical and giving the explanation. If it's correct, then the universe may actually be 47 (not 13.8) billion years old, corresponding to 47 billion light years of the observable universe radius. I don't deny that matter is 13.8 billion years old and I don't claim that universe is 47 billion years old in proper time. I claim that it's 47 Gy old in conformal time, and that conformal time is the actual cosmic time of the universe, not the proper time of its matter. I base my argument on the fact that the expanding universe without matter would not be its age, because it wouldn't have it, but it would still be aging - conformally, along with the decreasing energy density and temperature of the background radiation. Answering the title question: The universe itself would be aging - conformally. Astronomy is in Crisis... And it's incredibly exciting - Kurzgesagt - https://youtu.be/zozEm4f_dlw In summary: 1. Dark matter distribution doesn’t exactly fit the galaxy rotation curves. 2. Dark energy doesn't exactly fit the expansion. There are serious premises of a non-accelerating expansion based on "strong progenitor age bias in supernovae". 3. Hubble tension remains a persistent and unsolvable mismatch between the expansion rates. 4. There are so old galaxies observed in such a young universe, that ΛCDM model simply doesn’t allow them. 5. These galaxies can have from 1% to 100% contribution to the CMB radiation. How funny is that? 6. The excess radio dipole doesn't match our peculiar velocity calculated from the CMB dipole. Plenty of things simply don't add up. Quite positive and interesting feedback from scienceforums.com: https://www.scienceforums.com/topic/98751-what-would-be-aging-in-the-expanding-universe-without-matter/#findComment-465635
-
Physical, conformal age of the universe
So 3000K was a temperature of hydrogen back then?
-
Physical, conformal age of the universe
In my understanding, the background radiation was already there before the recombination, when the hydrogen atoms were created, and some of it was absorbed by them in the process of their creation. However, the electrons in newly formed atoms were generally in the excited state from which they immediately transitioned to the ground state, emitting the photons that were added back to the background radiation. Is this correct? If it is, then the idea of extrapolating it back to the Big Bang seems sensible to me the more if the radiation coexisting with the plasma before the recombination was the black body radiation. If it's not, then I'm left with the purely mathematical extrapolation, but I don't see how it could be incorrect, since the radiation's redshift directly corresponds to the scale factor describing the equal expansion of the universe and the radiation filling it. What I can show is trivial. "According to the FLRW metric which is used to model the expanding universe, if at present time we receive light from a distant object with a redshift of z, then the scale factor at the time the object originally emitted that light is a(t)=1/(z+1)." [imath]1+z=1/a(t)[/imath] I'm aware that [imath]dz/dt = -\dot{a}/a^2 = -(1/a)(\dot{a}/a)[/imath] [imath]\dot{a}/a = H(t) = H(z(t)) = H(z)[/imath] [imath]dt = -(1+z)^{-1}H(z)^{-1}dz[/imath] [imath]dt/a(t) = -dz/H(z)[/imath] But I'm not using it; dz is the differential of dimentionless redshift, and I need dimentional, temporal dt and spatial cdt. It's enough for me that 1/a(t)=1+z(t), so dt/a(t)=(1+z(t))dt. Now, if we interpret dt as the initial period and cdt as the initial wavelength at - let's say - the Planck time, then z(t)+1 is the redshift+1 equal to the expansion of the wavelength, period and the universe itself. Ps. What's the deal with latex?
-
Physical, conformal age of the universe
I can't show it in "my" integral, because it's not mine. It's the integral of the FLRW metric equation for null geodesic. I'm just giving you my interpretation of cdt/a(t) as the extending wavelength, and dt/a(t) as the extending period over time counted backwards. Ps. I've reached the maximum number of posts I can make per day. That's a limitation for a new accounts on this forum. @swansont I will gladly answer you tomorrow.
-
Physical, conformal age of the universe
But I see it. If you extrapolate the CMB peak wavelength backwards to the Big Bang, then it will be infinitesimally short, just like the differential dt. That's why I consider cdt/a(t) as the extending wavelength, and dt/a(t) as the extending period, but with time counted backwards.
-
Physical, conformal age of the universe
I don't choose a single one. I'm adding their changing periods just like I'm adding a changing wavelengths by integrating over cdt/a(t) to get the observable universe radius. Conformal age 47Gy is conformal, because it's proportional to the observable universe radius equal to 47Gly, and the proportionality factor is the speed of light. In the same way the extending radiation periods are all proportional to the extending wavelengths. That makes them conformal.
-
Physical, conformal age of the universe
Which one are you? :)
-
Physical, conformal age of the universe
SI definition of a second: "The duration of 9 192 631 770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium-133 atom." If we give the cosmic time (equal to the universe age equal to the proper time of the observer resting in the CMB reference frame) in seconds, we can easily give it in the number of radiation periods from SI definition of a second. In the same manner we can define a physical, conformal age of the universe. That's the duration of a certain number of the extending CMB radiation periods proportional to the extending peak wavelength of this radiation that passed through a point at which the CMB is isotropic, since its emission. Proportionality factor is the speed of light, because c=λ/T where λ is the extending peak wavelength, and T is the extending wave period. Conformal time η=∫dη=∫dt/a(t)=47Gy is the conformal age of the universe and I don't question it. I'm proposing a physical definition for it. The inverse of the scale factor 1/a(t) is increasing with time counted backwards, because 0<a(t)≤1 and a(t₀)=1, where t₀ is the present, proper age of the universe. That makes dt/a(t) the equivalent of the wave period extending over time counted backwards. We're integrating over it to sum it up. Is there something wrong with the proposed, physical definition?