mattiao
Members-
Posts
10 -
Joined
-
Last visited
mattiao's Achievements

Quark (2/13)
2
Reputation
-
Dear Joigus, finally I have been working again on this topic after several weeks. While I confirm that with a system of 2 non linear equations and one parameter K, adding the condition of \[ \boldsymbol{\nabla}J = 0 \] works to find the maximum K for which the system has solution, when I try to apply it to a system of 3 equations, this method doesn't work. I do an example to work on it: \[ \begin{cases} 4x^3 - y + 4xy^2k = 0 \\ 4x^2y + 4y^3 - x - k = 0 \\ 2z + p = 0 \end{cases} \] First of all I have trying to iterate k and I found that the system has solution until \[ k<=6.9 \] resulting \[ x=0.0302, y=1.2008, z=-3.45 \]. Then I have calculated the Jacobian of this system: \[ J = \begin{bmatrix} 12x^2+4y^2k & -1+8xyk & 0\\ 8xy-1& 4x^2+12y^2 & 0 \\ 0 & 0 & 2 \end{bmatrix} \] Calculating the determinant of this I get \[ \boldsymbol{\nabla}J = 2(12x^2+4y^2k)(4x^2+12y^2)-2(-1+8xyk)(8xy-1) \] But if I add this equation to the above system, imposing it equal to zero, the system has not solutions. In fact substituting \[ x=0.0302, y=1.2008, z=-3.45 \] in the above equation, value is far from zero. Any idea?
-
Yes, now I would like to solve a system with 4 variables and 1 parameter, so in total 4 equations + the equation to close it maximizing the parameter. Unfortunately no... but if it helps we can consider it linear as first step and once solved, to move on non-linear.
-
Dear Joigus, I have been thinking and working at this topic and I have done some progresses! I have extended your intuition to systems with more equations. So if we have a system of 3 unknows and 1 parameter of which we want to find the higher value that makes the system solvable, we can use the parameter as an unknows and add a 4th equation. To write the 4th equation we can consider the gradient of the other 3 equations. We can do \( \vec{v_{1}} = \boldsymbol{\nabla}f_{1}\wedge\boldsymbol{\nabla}f_{2} \), so \( \vec{v_{1}} \) is the vector tangent to the curve created by the intersection of \(f_{1}\) with \(f_{2}\). In the same way we can do \( \vec{v_{2}} = \boldsymbol{\nabla}f_{2}\wedge\boldsymbol{\nabla}f_{3} \) to get the vector tangent to the curve created by the intersection between \(f_{2}\) and \(f_{3}\). Now to have just 1 solution of the system, we need that those 2 curves are tangent between them, therefore we can impose \( \vec{v_{1}} \wedge \vec{v_{2}} = 0 \) as 4th equation of the system. I have tried with many systems and it works!!! Let me know if what I have done until here is clear... because now I would like to do the same with more equations in the system, but it looks quite difficult! Do you have any idea how to continue?
-
Joigus, I think using \( \boldsymbol{\nabla}f_{1}\wedge\boldsymbol{\nabla}f_{2}=0\) as 3rd equation of the system, is the correct solution! I have tried with several systems of 2 equations and it always working! In the next days I will try also with systems with more than 2 equations... I will keep you update, thanks.
-
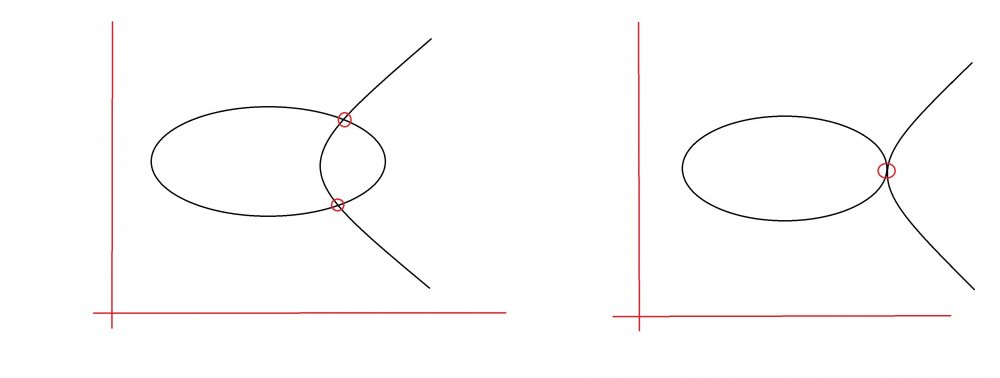
Yes joigus, I think we start to be on the right way. So, as you already understood, my system becomes: \[ \begin{cases} −x^2 + 10x − 1/2y^2 + 6y − K = 0 \\ −2x^2 + 20x + 3/2y^2 − 18y = 0 \\ (−2x+10)−(−4x+20)=0 \end{cases} \] And like you said, from the 3rd equation I get \(x=5\). Substituting this in the 2nd equation, we get \(y=4.367\) or \(y=7.633\). Finally substituting x and y in the 1st equation, we get \(k=41.667=\frac{125}{3} \) . So for this example imposing the 3rd equation as the difference of the derivates respect x, works. You can try to do the same with the second example, but in this case you have to derivate respect y to obtain the 3rd equation. Solving the system, you will get: \[x=1.6626 \\ y=6.0 \\ k=45.0\] that is exactly again the maximum value of k that we were looking for. The reason is that the 3rd equation adds the condition of tangency between the 2 intersection of the surfaces represented by the first 2 equations with the plane xy. So , because they are tangent, the solution of the system that is the intersections of the previous curves, can only be 1. I show you both cases in the following picture: So, they case on the left that has 2 solutions is for \(k<125/3\) and the case on the right with just 1 solution (tangency between the 2 curves is \(k=125/3\). If we have \(k>125/3\), the 2 curves doesn't intersect and there isn't any solution.
-
Hi Joigus, sorry if I haven't been clear enough, I'll try to explain better. It's true that the equation in the example can be solved exactly, but as I explained, that was just an example, my system is done be 4 equations and it can't be solve analitically, it has to be solve with numeri methods (Newton-Rapson in my case). I try to change example, anyway keeping just 2 equations to start: \[ \begin{cases} 30sin(x/4)+100sin(x/10)-x − 1/2y^2 + 6y −k= 0 \\ 60sin(x/4)+200sin(x/10)-2x + 3/2y^2 − 18y = 0 \end{cases} \] I am trying to use k as a new variable and to add a condition of uniqueness in the 3rd equation. Because the number of solutions of a system of 2 equations can be N if the equations intersects in the XY plane N time, 0 if they don't intersect or 1 if they are tangent, I am trying to impose the tangency condition. Therefore as 3rd equation I use the difference of the derivate of the 1st equation and the second equation respect the same variable. For example in the first system I proposed it worked with the derivate on X, instead in this last example I have to derivate respect Y. In both cases anyway with this approach, I get the correct solution. Have I been more clear now?
-
I am considering K as an independent variable, so our system becomes: \[ F(x, y, k) = 0 \] The third equation is the Jacobian of the first equation respect the first variable (x) minus the Jacobian of the second equation rw respect again the first variable (x). So for the example I put above, it becomes: \[ (-2x+10) - (-4x+20) = 0 \] The reason why add this 3rd equation is that solving this system with Newton-Rapson I got the result I was looking for. Otherwise I don't see how to get it using numerical methods... P.S.: sorry but I am not able to write formulas in the correct way in this forum, please give me some advice...
-
ok, very good, but now let's complicate things... This is the analytical solution of this system. In my case I have much more complex systems and I can't analytically solve, so I use a Newton-Raphson method. I found I can get the same result (K=125/3), adding a third equation to the system and using k as a variable: df1/dx - df2/dx = 0 (the derivate respect x of the first equation minus the derivate respect x of the second equation) This makes sense, because it imposes that the intersections of 2 surfaces represented by the first 2 equations of the system with the plane xy, are tangent and this is the limit for which the system can have a solution. Please ask if I have not been clear enough... now, considering that my system has 3 equation (like said above that posted was only an easy example to explain the post), which equation should I use as forth one to find the maximum parameter for my system?
-
Thanks Sensei, the result is correct (K=125/3), but I have't clear how you found it. Can you explain, please?
-
mattiao started following System of equations and one parameter
-
Dear all, I have a system of N non-linear equations in N variables and 1 parameter. The system has solutions until the parameter is less than a certain value. I am interested in finding the maximum value of the parameter for which the system has solutions. Could you help me to find a way to do that? I have tried to use the parameter as an extra variable of the system and to add one more equation, but I struggle to find the new equation... I try to give you an example in case I have not been clear enough: −x^2 + 10x − 1/2y^2 + 6y − K = 0 −2x^2 + 20x + 3/2y^2 − 18y = 0 How do I find the greatest K for which this system has a valid solution? Note that this is only an example, I am looking for a general rule...