Martoonsky

Hi. Thanks for the the help, but I have a complaint. In your original post, you say to use math tags but you don't explain what the math tags are or how they're formatted.

@studiot, if we used the constants [math]\rho\left(R\right)[/math] and [math] g\left(R\right) [/math] then it would be true that [math] \int_{0}^{R} \rho\left(R\right)g\left(R\right)dr = \rho\left(R\right)g\left(R\right)R = P_{R} [/math].

However, this is not the case. When [math] \rho = \rho\left(r\right) [/math] and [math] g = g\left(r\right) [/math] then in general, [math] \int_{0}^{R} \rho\left(r\right)g\left(r\right)dr \neq \rho\left(R\right)g\left(R\right)R [/math]. Note also that [math] \int \rho\left(r\right)g\left(r\right)dr \neq \rho\left(r\right)g\left(r\right)r [/math]. If you still disagree with the math, then please show your own working out.

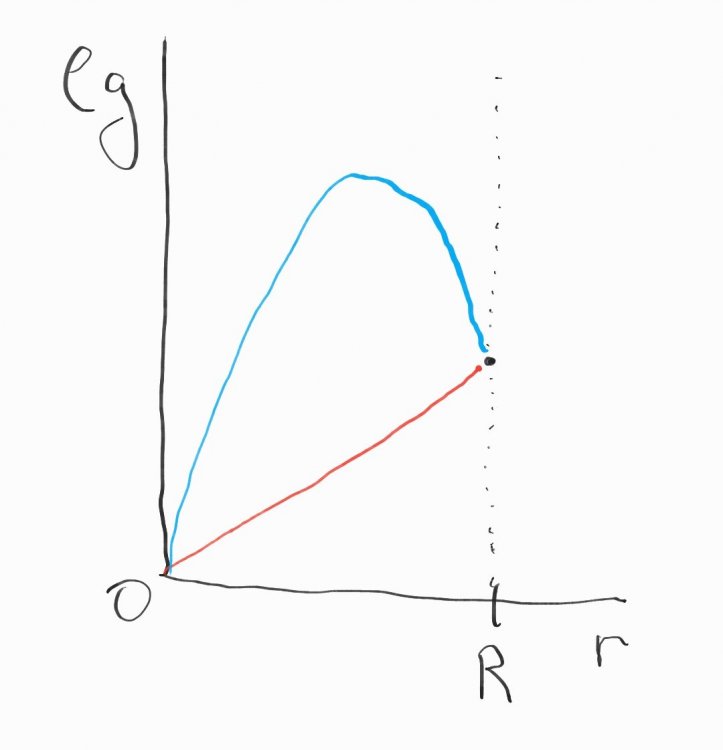
@joigus, I was not trying to represent any particular formulas in my graph. I was just trying to point out graphically that two different functions will not have the same value of definite integral over the interval [math]r = 0[/math] to [math]r = R[/math] just because their endpoints have the same value.

3 hours ago, studiot said:

Thus your expression states

P₀  =  P_R  + P_R  = 2 P_R

Sorry, but this is not correct. If rho and g were constants, then the integral would evaluate to P-sub-R, but they are not. Check out the graph below of two possible curves for rho x g vs r. They have the same values at r=0 and r=R, but obviously their integrals are not the same. 

7 hours ago, joigus said:

1) the amount of air within the shaft does not deplete the atmosphere significantly

I don't see this as much of a problem theoretically. You could make the shaft very narrow, or add air. If the atmosphere were depleted, it would reduce the value of the pressure at the center. 

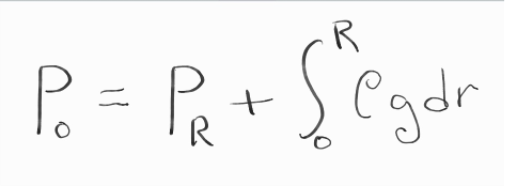
I haven't yet tried to do a detailed calculation but the above graphic provides the answer. P-sub-zero is the pressure at the center (at radius r = 0). R is the radius at the surface. Rho = rho(r) is the density and g = g(r) is the acceleration due to gravity. 

I thought I would divide the integral into sections for the inner and outer cores, mantle and crust. I think I could come up with an average g for each section. I'm not sure what to do with rho yet since it varies with temperature and pressure. 

56 minutes ago, Endy0816 said:

I think if the Earth were to stop spinning and had all of its mass evenly distributed in a sphere, it would be close to zero at the exact center.

 

Thanks, but I'm pretty sure that's not correct. Air pressure is due to the weight of the air column above you. As you go down into the earth, the air pressure should rise above the atmospheric pressure at the surface. Among the factors involved, you would have to account for the acceleration due to gravity decreasing as you go down; also, assuming the walls of the tunnel allow heat to flow through, you'd have to allow for the temperature increasing as you go down. 

I wonder if anyone has any ideas as to how one might figure this out. If there were a tunnel from one side of the earth, through the center of the earth, and on out the other side, what would the air pressure be in the center? I have some ideas, but one catch is that the air pressure and air density would seem to be mutually interdependent..