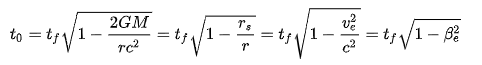rjbeery

No problem. Please provide me with an exact equation showing me this.

OK, so I've never looked at the derivation of the approximation before. This is a great synopsis: https://campus.mst.edu/physics/courses/409/Assignments/gravitational potential.pdf I think I understand. The approximation U = mgh has 'g' baked into it; we could rewrite this as g = U/mh, and if we take the derivative with respect to r (or h), the change in g is independent of a change in r (or h) in this form -- so you are right. However, the true math (sans approximation) is a full Taylor series expansion, with the height variable continuing on indefinitely to higher and higher powers. In other words, the full expression of g = U/mh is infinitely differentiable with respect to r and will always be dependent upon r. There is no scenario where the acceleration can exist in a form that is independent of r. So, yes, the approximation is exactly the cause of our disagreement.

I think it's important that we agree on where we disagree. I don't deny anything about Einstein's elevator, except that it isn't a true equivalence if the acceleration is due to gravity, and that's because I don't believe "constant acceleration due to gravity" is possible, and the Newtonian approximation is obfuscating that fact. Light would obviously bend under acceleration, regardless of the source. You're asking me to prove that your approximation is an approximation. I may look at doing this, but at this point I don't see much benefit in convincing you as long as you haven't found any objective refutation in the mathematics of my paper.

It doesn't give the same answer. Saying "the other [terms] are small and can be ignored" is like saying that pi is literally 333/106. If Einstein's elevator is your example of a physical scenario where potential increases over a substantial distance of constant gravitational acceleration, it isn't valid. It too is an approximation. We can imagine, in our minds, an elevator being accelerated uniformly from top-to-bottom, but the person standing in the elevator could use equipment (available today) to compare the gravitational acceleration at his head vs his feet. If they differ then he knows he is in a gravitational field. A gravitational field is defined as the negative of the gradient of the gravitational potential. If the gradient is zero, then the gravitational acceleration is zero -- how would you explain that?

But it isn't. I agree with you that time dilation, and therefore refraction, are correlated with gravitational potential, but a change in gravitational potential requires a change in time dilation. I have given the full GR treatment of velocity and how it relates to a free fall in gravity in equations (1)-(6). I do the same in the second section with refraction. Yes, I did this, and we both agree that my math is an exact result, whereas the Newtonian approximation used by Pound-Rebka is just that. It is known to be inexact, and would quickly diverge from reality as the height of the tower increased. In other words, you're using a known approximation as a proxy for GR when we both know it is not. If you still disagree then I would like to examine a physical scenario where potential increases over a substantial distance of constant gravitational acceleration. The only one I can think of is in the center of a Newton's sphere (where potential remains unchanged).

I understand now. You think that, because the approximation has varying time dilation with a constant g, then that's proof that GR claims the same thing. This is false, and equivalent to saying that Newton's approximations prove that the speed of light is infinite.

What different result were you referring to here? To be honest, the things you're saying are just bizarre. This is from the Pound-Rebka wiki page: In other words, treating g as constant is a known approximation, and the proper calculation is literally listed. I solved that exact calculation to show you that it does not produce a "different result". If we used exact values for r_s and altitude then it would produce an exact result.

I can't tell if you're being intentionally obtuse, but .009 is the approximate Schwarzschild radius of the Earth. I used that for r_s in the calculation. The above math was my response to you saying where the ratio of time dilation factors (using rough estimates) is a difference of 3*10^(-15), compared to the gh/c^2 = 2.5*10^(-15). The fact that they could not (at the time) measure the time dilation difference at a distance of 22.5 meters, forcing them to use the approximation you listed, does not mean that the GR answer is anything but correct.

Have you done any calculations? and gh/c^2 = 2.5×10^(−15)

This isn't true; the frequency shift you're using is a Newtonian approximation. Compare this (the true equation): to equation (12) in my paper above and you can see that they are clearly just taking the ratio of time dilation at both heights to determine blueshift.

There's nothing controversial in the paper. It's very straightforward. If you think this paper is inconsistent with GR then you are perhaps misrepresenting what GR predicts. I don't understand the second statement above. I'm not sure how (or why) I would want to derive time dilation without GR. Lastly, time dilation would exist in constant g but it would also be constant, and therefore gravitational acceleration would not be present. Consider the inside of a massive, transparent Newton's shell -- time moves slowly, but everything is free-floating.

According to this paper, "constant gravitational acceleration" would not induce forces at all. I mean, intuitively, we would expect it to (because we are accustomed to using g for convenience) but, as the paper outlines, time dilation would be constant in a field of "constant gravitational acceleration" and therefore would not refract light. If gravitational forces still existed in such a field then equivalence would be broken. Also, you are asking for the causal mechanism, but that is literally what the paper is about. Time dilation is the mechanism. If you're driving on a dirt road and you hit the shoulder of sand, your car turns in that direction; drop a straw in water (where light moves more slowly) and the straw appears to "bend down". It's all the same thing.

I copied your post above, but here's a direct link: https://www.scienceforums.net/topic/122084-paper-a-causal-mechanism-for-gravity/page/2/?tab=comments#comment-1141752 I'll be curious to see if others find this result unsurprising as well. I think it is very significant.

You asked for an explanation 11 months ago, and now you seem to be saying that it's obvious.

swansont, I feel that this paper is a completely different angle on a similar subject. Please consider letting it remain in its own thread. equation (19) should read:

In this paper, we show that the time dilation field of mass-energy is sufficient to predict gravitational effects on light. Essay written for the Gravity Research Foundation 2021 Awards for Essays on Gravitation. Free-falling into Black Hole We start with a black hole, B, possessing a Schwarzschild radius (rs) of 3000 m, giving it a mass of roughly one solar-mass (~2*10^30 kg). We take a body, A, of negligible mass, initially resting at a great distance (PEi = KEi = 0), and allow it to free-fall towards B. To calculate A’s coordinate velocity at a given distance, r, from the center of B, we start with (1) (2) (3) (4) (5) so (6) Integrating gives us: (7) We evaluate the equation for the final 1000 meters of A’s path before reaching the event horizon (i.e. r = 4000..3000, see Fig 2) (8) (9) So (10) Here we take note of the proper velocity of A at r = 4000 (see Fig 2) (11) We also note that (12) where t0 is the proper time of events for A, tf is the coordinate time of those same events (for a distant observer), and the radical value is the time dilation factor which approaches 0 as r approaches the event horizon at rs. Light passing through a graded refractive index A refractive index of a medium is defined as the dimensionless number (13) where v is the measured velocity of light through that medium. In other words, n can be treated as the reciprocal of an apparent time dilation factor (from the remote observer’s point of view). If we consider a gravitational field as the medium being traversed, then we can use (12) to represent that medium’s refractive index as (14) where ys is analogous to the Schwarzschild radius of B above. We see that as a light ray R approaches a height of ys the “time dilation factor” approaches zero, and n diverges to infinity. Light in this area is effectively frozen, and, for all intents and purposes, the horizontal boundary of y = ys is an event horizon. Now we take Snell’s Law (15) where k is a constant determined by the initial angle and location in the medium of an incident ray. Combining (14) with (15) we now have (16) so (17) In Figure 1 we are considering theta to be the angle between R and the normal to the x-axis, therefore (18) We can combine (16-18) to get (19) We now want to determine k. Since we know from (11) that the body A is approaching B at a velocity of .866025c at r = 4000 (see Fig 2), we choose theta such that the light ray R is approaching B at the same rate at y = 4000. A light ray with a vertical component moving downward at .866025c is doing so at pi/6 radians off the y-axis (20) (21) (22) All such k-values will be unity when the vertical component of R is equal to a radial free-fall velocity, such as A’s, at a given height. Plugging k = 1 into (19) we have (23) We now calculate the length of R’s spatial path from y = 4000 to the so-called event horizon ys = 3000. (24) (25) (26) (27) (28) So (29) which is the same value we calculated in (10). Gravity and refraction equivalence We can verify the relationship between (8) and (27) by adjusting (7) (30) (31) (32) where of course the constants of integration are irrelevant to the integral. Conclusion In conclusion, we have shown that the time dilation field of mass-energy predicts gravitational effects on light. Parsimony and equivalence would suggest that this mechanism is sufficient to explain gravitational forces on massive objects as well, possibly in the form of EM mass.

I have some questions regarding black holes. Which forum channel would be appropriate, and do we happen to have any astrophysicists on this forum?

Markus, may I ask your profession?

Agreed. I'll post to the forum if and when I find or produce a new analytic solution. Thanks so much for the patient and mature discussion.

Have you actually read the OP? Or its references? Did you look at the numeric analysis I posted? I shared the spreadsheet so you can see that there are no fudge factors involved. The math works. That being said, I understand the tensor objection, which is why I'm asking for real-world examples where spacetime curvature and time dilation diverge. Maybe the full time dilation field requires more information than I'm presuming; maybe GR has redundancies in distinguishing mass/momentum and other forms of energy (IOW, two different systems could produce the same result); maybe there's more information in the EFEs than mere spacetime curvature; maybe this connection doesn't generalize and is only useful in limited analyses. I think about all of these things. But insisting that either this idea can either immediately and completely replace all of GR, or else it's worthless, seems premature.

Feel free to throw out thoughts, I love hearing other perspectives. Dispersion and FLRW are things I had never considered, and I appreciated their mention.

Markus, I understand your position and I appreciate your input. You're correct that I keep referring to the simpler Schwarzschild spacetime solution but that was to illustrate the theoretical connection to others who can't see it at all. I'm "facing many fronts" in this thread. I just spent 6 hours convincing another poster that the gravitational time dilation equation is mathematically valid. You might be right that the connection doesn't generalize, but I remain unconvinced. The FLRW spacetime example doesn't work, for example - the reason we know about cosmological expansion in the first place is due to time dilation (red-shifting of the distant stars). In fact, when people present me with apparent counter-examples that I can explain it does nothing but strengthen my resolve. If that's frustrating, I'm sorry. This is right but we've already covered it. It's the local time dilation gradient that determines gravitational movement. Remember discussing Newton's shell?

I'm ignoring nothing. There are time units on the LHS (t0), and time units on the RHS (tf). The remaining units under the square root all cancel out. I literally did the math for you. Numerator units: GM = m^3/s^2 Denominator units: rc^2 = m^3/s^2 They are the same units. Meters cubed over seconds squared. What are you missing?

Mordred...you're peer reviewing PhD astrophysics articles and you've never seen or dealt with the gravitational time dilation equation? Look at the numerator of the fraction under the square root: 2GM. This has units of m^3 * kg^-1 * s^-2 * kg. This simplifies to m^3 * s^-2 Look at the denominator of the fraction under the square root: rc^2. This has units of m * (m/s)^2. This simplifies to m^3 * s^-2 They cancel. It's a dimensionless scalar, as I've said multiple times. It's OK to miss a mass term in the numerator, or whatever you seem to be doing, but I don't understand how you aren't reading the words that I'm typing, explaining what the equation is, telling you exactly what you're looking at. If you don't like the equation, your problem is not with me but with the entire astrophysics community.

No, you need to read the words I'm typing. The first equation is the equation for gravitational time dilation. I'm pretty sure the dimensions align without problem.