
Casio
-
Joined
-
Last visited
Posts posted by Casio
-
-
On 6/29/2024 at 11:43 PM, studiot said:
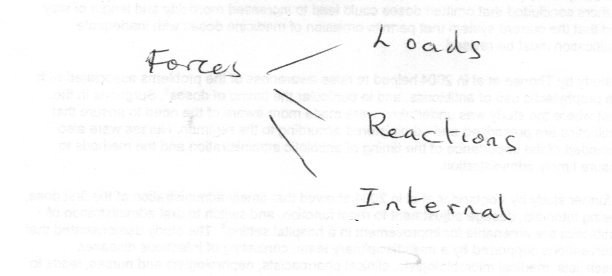
In Engineering we deal with real world objects called Bodies.
Bodies can be affected by agents we call Forces according to specific rules.Individual forces cannot combine directly, but many forces can act on a single body - with the overall effect being a specific combination of the effect of each force acting individually.
The same effect as all these combined forces can also be caused by a single suitably applied force called the resultant.
Because both bodies and forces exist in the same geometrical universe or framework, there exists a correspondence between the geometry of the lengths and positions of the bodies and the geometry of the diagrams describing the forces.
In fact one is a scale diagram of the other.For our present purposes forces acting on a by may be considered as
a) Externally Imposed - These are called Loads
b) Constraints on the Body by other bodies or forces - These are called Reactions
c) Forces generated internally witin the body by the actions of (a) and (b)
We will only need to examine (a) and (b).
Rules for the actions of Forces on Bodies
-
A force is a push or a pull
-
All forces act only in straight lines, called their line of action.
-
Forces cannot "turn corners" or "change direction" Interaction with a body may produce a new force in a different direction.
-
Individual forces generally act on bodies at a single point called the point of application.
-
A body for which the resultant of all acting forces is zero is said to be in equilibrium.
-
A consequence of (5) is that a body with only a single non zero force acting on it cannot be in equilibrium.
-
If a body is under the action of two forces it can only be in equilibrium if the two forces are acting along the same line.
-
A body under the action of two or more (non zero) forces may always be brought into equilibrium by the application of an extra single force whcih is equal in magnitude but opposite in direction to the resultant of the original forces. This is callant the equilibrant.
(This forms the force basis of the triangle of forces).
- The nature of the geometrical link between the configuration of the points of application and the directions and magnitudes of the applied forces enables a diagram called "The Polygon of Forces" to be either drawn or calculated.
Scale drawing alone was once a popular method of obtainingt the Resultant/Equilibriant without calculation.
The Triangle of Forces is simplest such polygon and uses three forces, two applied plus the resultant/equilibrant
In the next post I will show how this is done using some simple example diagrams.
I will also comment on where and why your information is correct or incorrect.
I also think you are perhaps confusing the obtaining of a resultant by the triangle of forces with resolving a single force into components in specific directions, which the triangle can do for you because of the aforementioned geometric relationship. But this is a different calculation altogether.
In the next post I will show how this is done using some simple example diagrams.
I will also comment on where and why your information is correct or incorrect.
Also, just in case some information NOT INCLUDED by me was overlooked, the Right Triangle is ONLY showing one force and half the calculations. In Vectors there must be two forces to find a resultant etc. I only included one. In a brake drum assembly, there are two shoes, one leading and one trailing. I only ever talked about forces acting on the trailing shoe using a Right Triangle. I also agree that force cannot turn corners, but maybe the confusion was around two areas of my concern that may have been misinterpreted?
1/ The applied force of 102.3 N travelled along AB ONLY. There then is a frictional force created (uP) This frictional force amounts to 32 N. I didn't know whether in my calculations to include it or dismiss it?
2/ The force (I said) along BC is NOT redirected from AB.
3/ The force I calculated along BC being 81.1 N I am referring that force to or calling that force the "Component" force.
What do I mean by component force!
The brake shoe is metal, the lining material is a mixture of compounds and resin. The frictional force acting is 32 N. This force is the force on the shoe material and the rubbing surface of the brake drum.
This frictional force 32 N being pushed on the brake drum is a calculated force from the 102.3 N appllied force, but I think is a seperate force.
The force acting along BC I refer to as the component force. This is what I am trying to establish as the force building up inside the brake shoe itself. So Newton said, to every action there is an equal and opposite reaction, hence, the force applied at B towards C is the component force and I calculated that as 81.1 N. Now to achieve that force, the pivot at the heel of the shoe must maintain the shoe in that fixed position, therefore a reverse reaction is created equal and opposite the applied force. The shoe has now got an internal force present of 81.1 N.
So, how dense does the material a shoe is made from have to be? If the material is too thin the shoe will distort and break. The component force calculated is to help interpret what force what thickness material can cope with without distortion and damage.
Hence why I was thinking about vectors and forces to calculate the component force!
-
A force is a push or a pull
-
I didn't think the conversation being carried on was necessary. You pointed out that what I said was nonesense. I thought that if you'd ofunderstood what I was trying my best to explain, then you might of returned with some constructive suggestions and or applied math to show how its done, but you didn't so I took it you didn't understand what I was trying to do. I appreciate it difficult to interpret people and ideas on such forums as these, but at least I tried. If it loads I've now included a diagram.
-
4 hours ago, studiot said:
Forgive me for knowing what i am talking about.
You posted Applied Mathematics in the Analysis and Calculus subforum where it is certainly misplaced, but i thought it a small point, easily rectifyable.
Perhaps @swansont would be kind enough to move it to Applied Maths where it truly belongs.
So what is the triangle if it is not part of the physical world?
This is just incorrectly imagined nonsense, as written above.
It certainly has little or nothing to do with the 'triangle of forces'
Ok thanks for your input anyway. I'll need to find an engineering forum that has experience in these areas of expertise.
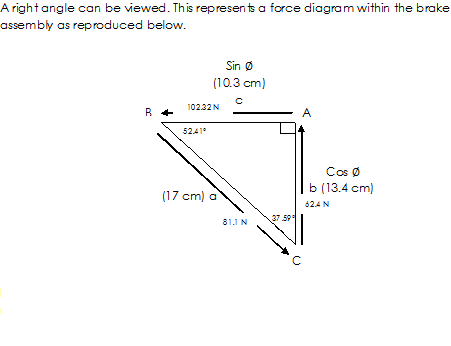
Ok I've managed to work out how to do it.
I've got a force of 102.31 N acting along AB. I wanted to work out the force acting along BC and CA. I knew that some losses must occur due to the angles the forces had to pass round. This is how it is done...
F Cos theta = 102.31 N x cos 37.59 = 81.1 N, and F cos theta = 102.31 N x cos 52.41 = 62.4 N
Now using Pythagorus we have...
c = square root a^2 + b^2
c = square root 81.1^2 + 62.4^2
c = 102.32 N
In conclusion...
Force AB applied was 102.31 N, the two remaining forces acting after the acute angles are; 81.1 N and 62.4N
That's good enough for me to give me some guidance, and I'm seriously NO expert in this.
-
8 hours ago, studiot said:
Thank you for your reply.
I am still not clear what is going on here and therefore what your actual question is.
Can you (scan/photograph) and post the passage from the book as printed please.
You need to be aware that there are (always) two triangles involved.
There is the real world-object triangle which defines the geometry of the situation, both in terms of distances / positions and angles.
And there is a purely theoretical abstact triangle others have referred to as a vector triangle.
This second triangle is similar to, but not congruent with, the real world triangle.
Two triangles are said to be 'similar' if they have the same angles, but not generally the same side lengths.
Triangles which have both the same angles and the side lengths are said to be congruent.
I am guessing that mixing up these two different triangles is the source of your difficulty, but I can't be sure without sight of the original.
Thanks for your reply. The triangle is imaginary and is not similar to another triangle. I'm no professional in this subject, but another book I've researched suggests I should have posted this problem in the Statics forum and not the maths department. If I can find away of posting my drawing I'll do it as soon as I can, but I think you could also get a good general idea of my request by drawing a right triangle on paper yourself to give you the picture I'm referring to.
The specifications...
Right triangle.
The 90 degrees angle MUST BE at the right corner of the horizontal line, i.e. __________________Here. Then follows the vertical line downwards, i.e. | This line touches the horizontal line marked "Here". That is the 90 degree angle point. The horizontal line length is 10.5 cm. The vertical line length is 13.5 cm. The line that represents the hypotenuse is 17 cm. The triangle has acute angles, the top left is 52.41 degrees and the bottom angle (sine) is 37.59 degrees.
My problem...
An applied force is present along the horizontal line from A to B. A is the 90 degree angle. B is the 52.41 degree angle to the left. When the force of 102.31 N is passed along the horizontal line from A to B, the line changes direction along BC, which is the hypotenuse, which then changes direction again by 37.59 degrees along CA to the 90 degree start point.
The force must change its magnitude when it changes direction. What I'm trying to find out and learn is how to use the acute angles in the math to calculate the new forces along BC and CA.
I hope you understand what I'm trying to do!!
-
On 6/23/2024 at 4:35 PM, studiot said:
Yes I think you may be missing something.
Is your triangle a real object like a triangular shelf bracket, say a length of strip metal bent into a triangular shape ?
No, the triangle is representing forces. In this right triangle, there is only one force N applied. This force then meets and equal and opposite force at point B in the right triangle, and then that force changes direction by 52.41 degrees and travels along the hypotenuse BC, before changing direction again by 37.59 degrees back to point A which is the right angle 90 degrees, where the applied force starts. Because only one applied force is known, in my understanding, until the angle 52.41 degrees is taken into consideration to change the direction of the force applied, then the force along BC cannot correctly be calculated.
So the engineering book I'm reading advises to measure the length of the sides of the triangle and multiply that length by the force applied to justify the force acting in that direction, such as the force from AB = 102.31 N times 10.5 = 1074 N, and then the force is applied again along BC = 102.31 N times 17 = 1740 N
So by just calculating two sides, the applied force is increasing after changing direction of 52.41 degrees. I just can't accept that the method used is correct?
Forces changing direction like this to me I'd think should reduce in force, not increase?
-
-
51 minutes ago, joigus said:
How come you multiply force times distance to get a force? The result would have to be a work, energy, torque...
(Never mind the mixed units, as you should convert cm to m.)
This should be homework, right?
First answer, multiply force x distance to get a force? Your not creating a force doing that, you've already got the force, its just increasing along the line of action.
Strickly speaking yes in the SI Units the length should or could be metres m, but equally so the units cm are also used. Common sense must prevail, if then your measuring a football pitch, by all means use metres m, but if your measuring something approximately 50 mm long, then I'd of thought using either mm or cm would suffice. The engineering book is using cm so I kept with that unit of length.
This is not homework. I'm simply reading at home in an interest I have based on my job I do. I'm nearly 60 years old and have no interest nor energy left for speed chalk board exercises that also envelope many mistakes.
-
I have a right angle, the 90 degrees angle is at the top right corner. A force is applied along AB. AB is the horizontal line from the 90 degree corner marked A to the left marked B, with a length 10.5 cm. The force along AB is 102.31 N. The force AC is the vertical line of action measured at a length of 13.5 cm. The hypotenuse final length BC is 17 cm.
Hope your with me to this point!
According to a engineering book I've read that includes the methods for calculating the Traingle of Forces, where two or more forces are known, the side lengths of the triangle are measured and then multiplied by the acting force to record the results, however, either I'm missing something in the writing of the book, or information is missing!
By example...
The force acting along AB is 102.31 N. The length of AB is 10.5 cm. Therefore 10.5 x 102.31 = 1074 N
Now the line of action changes direction from AB to BC, and this is where I'm questioning the book maths. The length of side BC is 17 cm, therefore 17 x 102.31 = 1740 N
I could carryout the same procedure with the remining vertical force, which records 1381 N.
What I questioning is this. The book example is using the Triangle of Forces Rules, but nowhere does the written instructions in the book take into consideration that these forces have changed direction, at angles of 52.41 degrees being angle ABC, and 37.59 degrees at angle BCA.
Am I missing something here? I'm sure the angles should be included in the math!!
-
-
On 6/23/2020 at 3:36 PM, John Cuthber said:
The Serpent pretty much did say "please eat this".
Don't forget that God put the serpent into the garden.
Nobody seems to know what He did that.From what I understand God put the serpent into the garden to watch over Adam and Eve. Although they were perfect that does not mean they knew or understood everything, they had not had the time to gain long term experience, which is not much different to us now. We all fall foul of some people who take advantage of us and we get what I call the short straw, which hopefully we learn by our mistakes not to get it again. It is said that Eve was deceived by the serpent who presented himself as a snake. Some talk about the apple, but I think it is more to do with understanding desire, the knowing and wanting something, so maybe it was more likely the serpent said something to Eve that caused her to take the bate. Presenting this bate (whatever it was) to her husband Adam caused him to agree with her which is where the problem with God arrived. God knew something was wrong at that time because Adam and Eve were said to be hiding in the trees, because they had become aware they were naked. Do children growing up not go through this very same experience, I think we all go through it.
The problem I have here is that we all die because through Adam sin past to all men, however conversations I've had over time people tell me that Eve was deceived. Maybe that could be true, however if I tricked you into something that would put your life in danger of dying, would that be your fault? If Eve was not to blame or partially to blame, she would still be here today, but she is not. It is also said that a balance had to be created to allow imperfect humans to co exist, so Jesus was sent to earth as a human sacrifice for all those who exercise faith in him. Where is Jesus our mediator today? He died over two thousand years ago, he made a name for himself but where is the real evidence that God or Jesus are real?
It is said that the bible is a book of knowledge that tells us about diseases and how to live etc, but take covid-19 now, did God instruct worshipers to stop socializing? No that was carried out by our governments, who took advice from scientists. Where is Gods involvement in the current world pandemic? Many and many questions but no evidence of a real world invisible God or Jesus.
-
As I have advised previously about this subject, I'm no expert or deemed to have any professional understanding of this subject, but a research medical journal I read advised back in 2017 about corona virus and trials that were being carried out back then. You start to get to a point that you hear people on the TV in the medical world with a lifetime of experience trying to advise you things that they are being told to keep their mouths shut about. Two doctors on the TV recently tried to speak out about this virus and one doctor was told to shut up and could not say what he wanted, and the other doctor had contracted the virus and since has past away. Recent information I've read had this to say about the corona-virus going back as far as 2017;
Ivermectin
Lab tests performed by Australian researchers showed that this anti-parasitic drug stopped the coronavirus growing in cell cultures within 48 hours. This widely available drug has already been shown to be effective against other viruses including HIV, dengue, flu and Zika.
Ivermectin is already approved by drug regulators and is widely available although it would have to be trialled in patients before becoming an accepted therapy.
-
19 hours ago, MigL said:
One factor which seems to be getting ignored during this outbreak, is the root cause.
Possibly because investigating it has racist overtones, but I think it can be discussed in a civil manner.India is as overcrowded as China and probably even more insanitary in certain areas, yet no major diseases have originated there.
China, on the other hand has given us SARS in 2004, and now COVID-19. Both are thought to have originated in Chinese 'wet markets", where exotic animals are caged in close proximity, under stress, and slaughtered on the spot for customers who believe their consumption provides health, sexual, and other benefits. Both virus are common to bats, and while SARS made the jump to civet cats, and then to humans, COVID-19 is thought to have jumped from bats to pangolins ( scaly anteaters ) and then to humans. Mutating with each jump.
Turtles, snakes, cats, birds, bats, etc. in close proximity, and a great demand from wealthy Chinese for these exotic meats is the root cause ( what benefits does shark fin soup really bestow ? ).These markets are common in China, Thailand, Vietnam, etc., where poor farmers can make good money by raising exotic animals that were never meant to be in proximity. China did close down some of these markets after the SARS outbreak, but they've looked the other way, as wet markets made a comeback ( as in Wuhan ).
Other diseases have also resulted from the overcrowded and unsanitary methods of raising pigs ( swine flu ) and chickens ( avian flu ).
Is it time that the world demands the ending of these wet markets ( especially the exotic animals part ), and other unsanitary livestock activities ?I'm no expert in this subject at all, and if it were not so affecting humans to the degree it is worldwide, I'd probably of never had an interest to look in on the subject at all, however, that said, I think that some serious questions must be raised to ALL world leaders after this COVID-19 is resolved, if it can be resolved as Russian indicate that it might never be resolved.
-
A lot is now being done where schools and business are closing although some business are doing their best to keep open and active. In my trade the government control us and are currently advising that we can't stop Statutory testing and examining motor vehicles. Today I've read about some businesses saying that they are asking customers to turn off their heaters and remove any items in the vehicles like food stuff, cans, cups etc. How serious should this vivid 19 be taken as a working class person dealing directly with the public!
-
Here is a Government UK link to statistics etc regarding the virus.
https://www.gov.uk/guidance/coronavirus-covid-19-information-for-the-public#risk-level
-
On 12/16/2019 at 1:34 AM, NonScientist said:
Okay, so I’m new here. Hi everyone.
So I’m not sure why this is affecting me this severely, but I recently discovered the whole “free will vs. determinism” question, and I’ve realized quickly that I should’ve never been introduced to this idea, because I’m finding it almost impossible to deal with the notion of not having free will. It has sent my mind into this state of extreme shock, agony, and despair that almost seems insurmountable. It’s like my whole world and everything I believed has been flipped on its head. I’m serious in saying that this has sent me into a straight panic and shock. I feel like I’m having this nervous breakdown. It’s an overwhelming feeling.
I’m trying to keep myself calm and just relax, but this has really messed me up.
Does anyone here believe in free will? Or can offer any good defenses or arguments for free will? I feel like I need to be reassured that there is free will or else I won’t be able to deal with it. The idea that everything is predetermined, and I’m just robot with no agency or ability to do otherwise is more than my psyche can handle. I’m sort of in this crisis.
One should always try to live a life as relaxed as one can in the circumstances. No matter what everybody might think or believe, nobody has complete free will. What you can and can't do will come from various sources, such as one's ability to understand what one might want to do in their free will, and a main one these days being the society we live in, which does control what we can and can't do quite a lot nowadays.
-
-
Triangle of forces
in Applied Mathematics
Why only AB?
The two problems I forsaw were...
1/ I only have one force N acting,
2/ The whole point of the excercise was to establish the component force, which you've pointed out as the internal force.
That is what I was always trying to establish. The force N acting along AB was always known, the problem was understanding how to work out the force internally (or along) BC to establish the internal (component) force.
Hope I've made that clearer, sorry if I've confused everyone.