Lazarus

The assumption in Bell’s Theorem is that in the Classic calculation the number of wrong way detections is proportionate to the sine of the angle of rotation. If the assumption were that it was proportionate to the 1- cosine of the angle the Classic and Quantum results would match. The reason that sine rather than 1- cosine was chosen is the question.

That's cool, uncool. That is 3 more errors than Bell's Inequality Theorem has. In spite of my sloppy post, the point is that the cosine relationship has not been justified.

In Post 41 Swansont said: You double the angle (according to the small angle approximation) and you double the counts in the orthogonal axis. The length of the orthogonal part varies as sin(x). That's basic trig. sin(2x) = ~2sin(x) for small values of x ------------------------------------------------------------------------------- Two plus two is four. Therefore, the moon is made of green cheese. For small angles the cosine is almost linear. Therefore, the cosine of the rotation of the measuring device matches the wrong way detections. That’s a hard sell.

Spin is usually concerned with a condition of a particle that resolves into two distinct choices, 0 or 1, red or blue, up or down, horizontal of vertical, etc. So what you mean by “projection of the spin” must be the projection of the polarized photon or bowing pin. The problem still remains “How does that justify the cosine of the angle of rotation of the measuring device matching the number of wrong way detections?”.

We are on the classic side of the fence, so how does spin relate to anything?

What is the justification for the cos detemining the number of "wrong way detections"?

There are two calculations, one Quantum and the other Classic that are being compared. The Quanum side is extremely complex but the Classic side is just High School Math so it should be resolvable to everyones satisfaction. The question is still "What is the justifcation for the rotated detector's wrong way detections matching the angle?". Here are some of the earlier posts. Post 25 Swansont I'm not seeing what the length of the horizontal line across the target area has to do with this. It's the angle that's being measured. Post 28 Lazurus The length of the pin is less than the long dimension of the rectangle and greater than the width of it. With the rectangle in the long direction vertical, a vertical pin will always go through. A horizontal pin will always hit the side of the rectangle. When the rectangle is rotated a bit the horizontal distance becomes greater and a horizontal pin has a better chance of making it through without hitting the side. Post 31 Lazurus Regardless of whether or not the Bowling Ball model is a valid demonstration of the failure of the assumption that doubling the angle of rotation of a measuring device can’t more than double the misses, what justifies Bell’s assumption that it is impossible for a physical situation to more than double the number of misses. Post 31 Swansont I don't think you've read that right, or didn't understand what's going on. As you change the angle of the detector, you start getting wrong answers. Classically it depends on the sine of the angle. For small angles, doubling the angle doubles the sine. But QM gives a different answer, which is how we know the classical analysis is wrong.

We discussed the reason for the assumption of the linear relationship and you wanted the vertical change to be the deciding factor and I wanted the horizontal difference to be the choise. Would you clarify why your position is better?

The essence of this discussion is that Bell’s Inequality Theorem relies on an unwarranted assumption. It assumes that the classic calculation of the number of “wrong way” detections in one of the detectors is linearly proportionate to the angle of rotation. There is no justification for that and it gives incorrect results. If the assumption were that the number of “wrong way” detections increased as the angle increased to the maximum, the result would be correct. That assumption is implicit in the Quantum calculation. If Bell’s Theorem is flawed Spooky Entanglement does not exist.

Thank you for the comments.

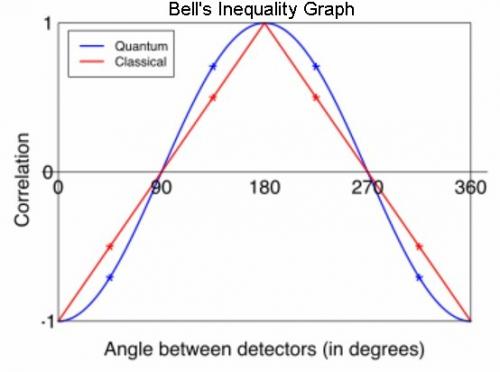
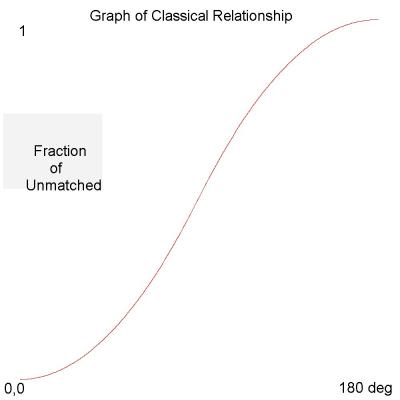
The state of the particles is not independent. Moving the angle of the second detector re-defines what you would mean by zero for an entangled system. I don't think you are appreciating the details of the physics involved. You appear to be thinking about this classically. Lazarus: The rectangle hole sensor should work OK for 90 degree correlations and it is easy enough to make a 180 degree correlation but that is irrelevant because YOU ARE ABSOLUTELY CORRECT that the measuring device doesn’t matter in Bell’s Inequality Theorem. What does matter is that Bell’s Theorem is based on the contention that the Quantum results cannot be matched by Classic physics but that is called into question. Here is a way to produce the same result without resorting to Quantum assumptions: The assumptions are that the number of unmatched pairs are detected is proportional to the angle between the detectors between 0 to 90 degrees. From 90 to 180 degrees the matched and unmatched numbers are reversed so the results are symmetrical. The conditions are that the Bob detector is stationary and the Alice detector is rotated and all the particles we are looking at are detected by the Bob detector as correct. At 1 degree the Alice detector receives 1 “wrong way” particle. In the 1 to 2 degree range the Alice detector gets 2 wrong particles for a total of 3 particles. For each 1 degree between 0 and 90 degrees all the Alice detectors wrong way particles are counted and added to a total. Since all of the Bob detectors are “right way” particles the number of unmatched pairs is equal to the Alice detectors total of wrong way particles for this degree of rotation. The total number of pairs is 8100. There are 45 pairs in each 1 degree. Here are the results: 1 deg of Total Deg Wrongs Wrongs Unmatched Fraction 0 0.000 0.000 0.000 0.000 1 1.000 1.000 44.000 0.000 2 2.000 3.000 88.000 0.000 3 3.000 6.000 132.000 0.001 4 4.000 10.000 176.000 0.001 5 5.000 15.000 220.000 0.002 6 6.000 21.000 264.000 0.003 7 7.000 28.000 308.000 0.003 8 8.000 36.000 352.000 0.004 9 9.000 45.000 396.000 0.006 10 10.000 55.000 440.000 0.007 11 11.000 66.000 484.000 0.008 12 12.000 78.000 528.000 0.010 44 44.000 990.000 1936.000 0.122 45 45.000 1035.000 1980.000 0.128 46 46.000 1081.000 2024.000 0.133 88 88.000 3916.000 3872.000 0.483 89 89.000 4005.000 3916.000 0.494 90 90.000 4095.000 3960.000 0.506 91 89.000 4184.000 3916.000 0.517 92 88.000 4272.000 3872.000 0.527 177 3.000 8097.000 132.000 1.000 178 2.000 8099.000 88.000 1.000 179 1.000 8100.000 44.000 1.000 180 0.000 8100.000 0.000 1.000 Graphs of Quantum results and Classic results:

---------------------------------------------------------------------------------- Lazarus: First, it has been claimed that no physical device could behave in the way that Quantum Theory dictates. That is what the bowling ball thing is all about.. Second, the above equation, f = theta squared divided by 2, shows that 2 degree rotation of one sensor gives a different result than 1 degee opposite rotation of both sensors as the sensors are independent. Are you suggesting that the 2 sensors are not independent?

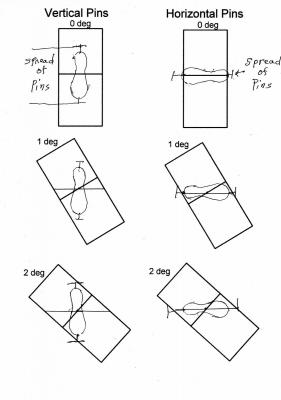
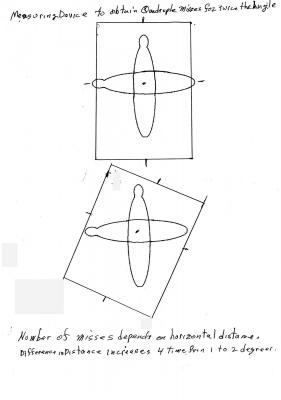
Swansont said: Your detector details are irrelevant. We're talking about the underlying physics, so the detection is assumed to be perfect. Lazarus said: The formula f = A^2/2, where f is the number of unmatched items and A is the angle of rotation, dictates different values for f when each measuring device is rotated 1 degree in opposite directions rather than one measuring device rotated 2 degrees. That is f = 2*1^2/2 = 1 for 1 degree vs f = 2^2/2 = 4 for 2 degrees. The 2 separate rotations are independent so must add to get the total number of mismatches. Experimental or theoretical corroboration of that would weaken Bell’s Inequality Theorem. Has that experiment been performed? Swansont said: Why will a perfect detector of bowling pin orientation measure the wrong spin the fraction of time you claim it will? Lazarus said: The detectors are rectangular holes that consider the pin detected if the pin passes through the hole without touching the edge. The vertical dimension of the hole is 1.5 times the length of the pin. The horizontal dimension is 0.99 times the length of the pin. The arriving pins have random variation of 0.1 times the length of the pin. When the rectangle is rotated the horizontal distance across it is equal to the width of the rectangle divided by the cosine of the angle of rotation. With the width = d0, the horizontal distance across with a rotation of 1 degree = d1 and with a rotation of 2 degrees = d2, d1 = d0/cosine(1) and d2 = do/cosine(2). Since d1 = d0*1.0001523 and d2 = d0*1.0006095 it follows that the increase in length of the horizontal distance across is 4 times as great for a rotation of 2 degrees as it is for a rotation of 1 degree.

Comparing bowling pins results with photon results: BOWLING PINS Two bowling balls are loaded into the chamber of a gun at a time, one vertical and the other horizontal. The chamber is spun, making the orientation of the pins undetermined but their relation of 90 degrees is constant. At some random time the pins are fired. Now the angle of rotation is determined but is unknown and the 90 degree relationship still holds. PHOTONS Radiation is split into two photons one polarized vertical and the other horizontal. The angle of rotation is undetermined but their 90 degree relationship is constant. -------------------- BOWLING PINS The detectors are rectangular holes that consider the pin detected if the pin passes through the hole without touching the edge. The vertical dimension of the hole is 1.5 times the length of the pin. The horizontal dimension is 0.99 times the length of the pin. The arriving pins have random variation of 0.1 times the length of the pin. PHOTONS The detectors measure the angle of polarization of the photons. The arriving photons have a random variation of 0.1 times the wave length of the photon. -------------------- BOWLING BALLS When the detectors are aligned with the arriving pins, there is a 100 percent match between the detectors. When one of the detectors is rotated 90 degrees there is a zero percent match. When one of the detectors is 2 degrees from alignment the number of mismatches will be 4 times as great as when the alignment is 1 degree off. The difference the horizontal distance available for the wrong way pins to get through is 4 times as great at 2 degrees as it is for 1 degree. PHOTONS When the detectors are aligned with the arriving photons polarization, there is a 100 percent match between the detectors. When one of the detectors is rotated 90 degrees there is a zero percent match. When one of the detectors is 2 degrees from alignment the mismatches are 4 times as many as when the alignment is 1 degree off. -------------------- What is the difference?

The point is that creating a scenario with bowling pins that gives the same results as Quantum entanglement questions whether or not the condition of the “Quantum” particles is really indeterminate while in flight.

The reason we have not been able to reach agreement is that not all the possibilities are being discussed. Using David Mermin’s explanation, which follows. a black and white distinction can be made. ---------------------------------- “Original Bell’s inequality The inequality that Bell derived can be written as:[4] p(a,c ) - p(b,a) - p(b,c) < or = 1 where ρ is the correlation between measurements of the spins of the pair of particles and a, b and c refer to three arbitrary settings of the two analysers. This inequality is however restricted in its application to the rather special case in which the outcomes on both sides of the experiment are always exactly anticorrelated whenever the analysers are parallel. The advantage of restricting attention to this special case is the resulting simplicity of the derivation. In experimental work the inequality is not very useful because it is hard, if not impossible, to create perfect anti-correlation. This simple form does have the virtue of being quite intuitive. It is easily seen to be equivalent to the following elementary result from probability theory. Consider three (highly correlated, and possibly biased) coin-flips X, Y, and Z, with the property that: X and Y give the same outcome (both heads or both tails) 99% of the time Y and Z also give the same outcome 99% of the time, then X and Z must also yield the same outcome at least 98% of the time. The number of mismatches between X and Y (1/100) plus the number of mismatches between Y and Z (1/100) are together the maximum possible number of mismatches between X and Z (a simple Boole–Fréchet inequality). Imagine a pair of particles that can be measured at distant locations. Suppose that the measurement devices have settings, which are angles—e.g., the devices measure something called spin in some direction. The experimenter chooses the directions, one for each particle, separately. Suppose the measurement outcome is binary (e.g., spin up, spin down). Suppose the two particles are perfectly anti-correlated—in the sense that whenever both measured in the same direction, one gets identically opposite outcomes, when both measured in opposite directions they always give the same outcome. The only way to imagine how this works is that both particles leave their common source with, somehow, the outcomes they will deliver when measured in any possible direction. (How else could particle 1 know how to deliver the same answer as particle 2 when measured in the same direction? They don't know in advance how they are going to be measured...). The measurement on particle 2 (after switching its sign) can be thought of as telling us what the same measurement on particle 1 would have given. Start with one setting exactly opposite to the other. All the pairs of particles give the same outcome (each pair is either both spin up or both spin down). Now shift Alice's setting by one degree relative to Bob's. They are now one degree off being exactly opposite to one another. A small fraction of the pairs, say f, now give different outcomes. If instead we had left Alice's setting unchanged but shifted Bob's by one degree (in the opposite direction), then again a fraction f of the pairs of particles turns out to give different outcomes. Finally consider what happens when both shifts are implemented at the same time: the two settings are now exactly two degrees away from being opposite to one another. By the mismatch argument, the chance of a mismatch at two degrees can't be more than twice the chance of a mismatch at one degree: it cannot be more than 2f. Compare this with the predictions from quantum mechanics for the singlet state. For a small angle θ, measured in radians, the chance of a different outcome is approximately f = θ^2/2 as explained by small-angle approximation. At two times this small angle, the chance of a mismatch is therefore about 4 times larger, since 2^2 =4. But we just argued that it cannot be more than 2 times as large. This intuitive formulation is due to David Mermin. The small-angle limit is discussed in Bell's original article, and therefore goes right back to the origin of the Bell inequalities.” ---------------------------------- We can agree that Quantum Theory predicts that the chance of a different outcome is approximately f = θ^2/2 and that experimental results have agreed with it. A 2 degree rotation should agree with the f = θ^2/2 number. However, Two 1 degree rotations should just add because they are independent. The question is “Were the experiments performed with a 2 degree rotation of one measuring device or 1 degree rotations of each measuring device?”.

Hooray! We finally agree on something.

The measuring device’s design determines the relationship between the angle of rotation and the results, not probability theory. Since s measuring device can be constructed that will match Quantum Theory results, Bell’s impossibility claim is wrong and Spooky Entanglement does not exist. Einstein’s contention that “Hidden Variables” really exist is consistent with this scenario. Schroeder’s cat is out of the bag. (or box)

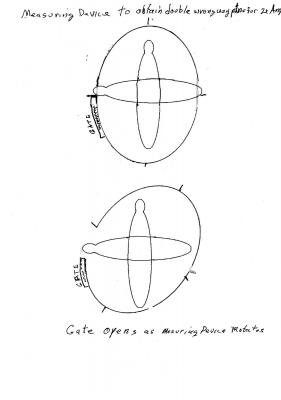
The reason to assume that doubling the angle doubles the wrong way photons is that probabilities add if they are not independent of each other. A measuring device can be constructed to match that assumption. The measuring device can be constructed to match Quantum Theory or something entirely different. To match the probability assumption, using orthogonal bowling pins fired at the device with a slight random spread, construct an ellipse with a door on the side that opens as the device is rotated. The long axis is slightly longer than the length of the bowling pin. The short axis is slightly shorter than the length of the pin. A pin that passes through is considered detected. A pin that hits the device is considered undetected. So doubling the angle will double the wrong way pins. To match the Quantum Theory result, use a flat sheet with a rectangular hole. Same rules, passing through hole is considered detected. The long dimension of the hole is slightly greater than the pin and the short dimension is slightly shorter than the pin. The distance available for wrong way pin to pass through quadruples when the angle is doubled. The relationship between the angle and the number of misses is dependent on the construction of the device so the assumption that doubling the angle always doubles the misses is flawed.

Rule # 92: If you can't answer a question, invoke "Authority".

Swansont said: polarized photons are 2.0001 meters long" because that's utter nonsense. Lazarus said: A photon with a frequency of149992500.3749812509374531 Hertz has a wavelength of 2.0001 meters, microwave range. Swansont said: said: You double the angle (according to the small angle approximation) and you double the counts in the orthogonal axis. Lazarus said: Why would that necessarly translate to twice as many wrong way detections. The difference in the length of the unorthogonal axis quadruples, which matches QM's numbers. The still is a "leap of faith" in the theory.

The mesurement is not in question. The Bell's contention that it is impossible to have a physical explanation is dependent upon his assumption that doubling the angle of rotation cannot cause more than double the wrong way photons. That is the point of contention.

Please, if you would, answer the double assumption question.

If doubling the angle = doubling the wrong way photons is not linear, it doesn’t matter. There has to be an excuse for assuming that to be the relationship. Also, 2 hundred years ago nobody cared about entanglement. The cosine thing does nothing to justify the assumption. It is fair to ask for a reason for assuming that doubling the angle doubles the wrong way photons.

Whether this example uses photons or sticks, the resultant pattern is comparable to the experimental results and to Quantum theory predictions. IMPOSSIBLE is a very strong condition but the Bell’s Inequality theory makes a questionable assumption about the relationship of the angle of rotation of one of the measuring devices and the number of wrong way protons detected. The assumption justification claims that no more than twice as many wrong way photons will be detected at 2 degrees of rotation than at 1 degree of rotation. Look at the way you and Bell justify it. “The length isn't what matters. The transmitted intensity depends on cos2(Ω) if Ω is the angle between the polarizer axis and the polarization direction. A classical measurement depends on cos(Ω). Plug in some small-angle numbers. You will see the variations are different by about a factor of two. e.g. 1- cos2(1º) = 0.000305 but 1- cos(1º) =0.000152” What is the evidence of a linear correlation between the cosine of the angle and the number of wrong way photons?