tmpst
Members-
Posts
21 -
Joined
-
Last visited
Content Type
Profiles
Forums
Events
Everything posted by tmpst
-
How is the spectral peak of a 2D wave spectrum defined when calculating e.g. the peak period or the mean direction at the spectral peak? Do you a) pick the point in the two dimensional frequency-direction space with the most energy, or do you b) integrate over all direction (thus turning the whole thing to a 1D-spectrum, and then pick the frequency with the most energy from there? For example in the spectrum with mock values: 0 deg 90 deg 180 deg 270 deg 0.1 Hz 0 0 0 0 0.5 Hz 0.1 0.3 0.5 0.2 1.0 Hz 0 0 1 0 method a) whould result in a peak period of 1s (1 Hz), and method b) in a peak period of 2s (0.5 Hz). The mean direction at the spectral peak would also differ, because it would be calculated over different frequancy bands.
-
Yes and yes. Constant atmospheric pressure will of course not show up in any partial derivates. But if the atmospheric pressure would drop at some point x, would that show as an decrease in the [math]\dfrac{\partial p}{\partial x}[/math] term, and thus inducing an increase in the [math]\dfrac{\partial u_x}{\partial x}[/math] term? This would mean a decrease in atmospheric pressure on the left side of the channel would induce a flow away from that area. I find this counterintuitive, as one would think that "pressing down" on the left side would cause the water to flow away from the area, not the other way around? In addition to the gauge pressure we have the dynamic pressure if we have any flow present, right? This is true, but here we have a flow entering the channel. This flow is due to some external force (e.g. wind, elevation) outside the channel. The external forces do not exist inside the channel. So we have a constant flow entering the channel, and we want to know how it is affected by the friction. Then I have to add the gravitational term to the NS-equation, right? This is interesting, but this case is about the attenuation of the flow due to the friction. Adding a gravitational term will not solve the question concerning the balance between the change in velocity and pressure, and the friction. After a quick glance, the Poiselle's equation is not applicable for my exact scenario, because it does not allow for acceleration of the fluid (an I assume a negative acceleration due to friction). That said, it is closely related and seems very interesting. Will definitely read up on it. Thank you.
-
Sorry about tha absence of a picture. I now have a picture of a scenario know. Please don't mind if this contradicts something I have said previously. I constructed this scenario to isolate the the terms I'm having problem with. So we have a constant flow that enters a bay. Because there is no driving force, the fluid will slow down due to the friction of the walls and the bottom. The fluid is incompressible, and we have no flow in the y-direction. The continuity equation is [math]\dfrac{\partial u_x}{\partial x} + \dfrac{\partial u_z}{\partial z}=0[/math]. We have no sink, so a change in velocity must mean a change in pressure, right? if the change of the velocity is negative, the pressure must rise. The change in velocity is due to the friction. In the x-direction the NS-simplifies to: [math]u_x \dfrac{\partial u_x}{\partial x} = -\dfrac{1}{\rho}\dfrac{\partial p}{\partial x} + \nu \nabla^2 u_x[/math] and in the z-direction to: [math]u_z \dfrac{\partial u_z}{\partial z} = -\dfrac{1}{\rho}\dfrac{\partial p}{\partial z} + \nu \nabla^2 u_z[/math] Now if we concentrate on the x-direction, how should I understand it? I'm pretty sure I'm not able to ask the right questions, but what exactly is the "pressure" here? Is it the dynamic pressure, the static pressure or the total pressure? How would a change in air pressuare be accounted for? My guts tell me that an increase in air pressure would result in an increase in velocity, so do you have to switch the sign when accounting for outer pressure? The viscosity term is reducing the velocity, but the reduction in velocity must then again increase the pressure. In my mind I would like to write then in two separate equations. The friction reduces the velocity [math]u_x \dfrac{\partial u_x}{\partial x} = \nu \nabla^2 u_x[/math], and the reduction in velocity increases the pressure [math]u_x \dfrac{\partial u_x}{\partial x} = -\dfrac{1}{\rho}\dfrac{\partial p}{\partial x}[/math]. When written in the same equation, the friction term is actually smaller then the reduction in velocity, which doesn't make any senso to me. Am I understanding the pressure wrong, or am I switching some sign somewhere? The second part that I find confusing is the value of the viscosity term. At the edges the shear stress is just the friction, but how do I get the shear stress [math]\tau_y[/math], say, 1m from the edge? By definition it follows from knowing the gradient of [math]u_x[/math] as a function of [math]y[/math], but that is exactly what I am trying to calculate. Is there some law or rule that says what kind of relationship there is between the shear stress and the distance from the wall? It can't be linear, because then the shear stress would be constant in the whole bay due the symmetrical situation. It feels that I am making some wrong assumption, or misunderstanding something. Then I'm just going thrue the same steps over and over, but they don't add up, and I can't really put my finger on the problem. PS. The increase in pressure could manifest itself as a rise in water level, right? Would the whole term then be accounted for by change in the static pressure, or should I always use the total pressure (unless I decide to use an approximation). If no rise in water level is possible, would the change in pressure then reduce to a change only in the dynamic pressure?
-
I have come to see that I have to allow for difference in pressure, so [math]\dfrac{\partial p}{\partial x}[/math] is not assumed to be trivial. I can obviously assume a wind forcing [math]\tau_w[/math] within the viscosity term in the x-direction instead, right? It all comes down to, that I can't seem to wrap my head around how the term [math]\nu \nabla^2 u_x[/math], which reduces to just a [math]\dfrac{\partial}{\partial y}[/math] term, affects the [math]u_x\dfrac{\partial u_x}{\partial x}[/math]-term. If we have no friction, then e.g. it makes perfect sense to me, that a reduce in pressure (so an increase in the [math]-\dfrac{\partial p}{\partial x}[/math]) would be balanced out by an increase in the velocity. In our case that increase in in velocity will be thwarted by the viscosity term in some proportion to the distance to the edge. But I don't "see" the connection between the derivate of the velocity in the x-direction, and the second derivate of the velocity in the y-direction. How do those cancel out? Should I be thinking of the viscosity term as being a "profile" of the the magnitude of the friction near the edge? I really appreciate everyones help this far.
-
Ah, thank you. It's obvious now.
-
The significant wave height is defined as [math]H_s = 4 \sqrt{\sigma^2}[/math], where [math]\sigma^2[/math] is the variance of the surfave elevation. The variance of a sine wave is [math]\dfrac{a^2}{2}[/math], where [math]a[/math] is the amplitude of the wave. A single wave [math]sin(t)[/math] thus has a variance of [math]\sigma^2 = \dfrac{1}{2}[/math], and a significant wave height of [math]H_s = 4 \sqrt{\sigma^2} = 4 \sqrt{\dfrac{1}{2}} \approx 2.83 m[/math], while the wave height of the sine wave is only [math]2 \cdot a = 2 m[/math]. How is this possible?
-
You are still missing the [math](u \cdot \nabla)u = u_x \dfrac{\partial u_x}{\partial x}[/math] term on the left, which is not zero. Assuming stationary conditions, the term on the left in your equation should be zero i.e. [math]\dfrac{{\partial u}}{{\partial t}}=0[/math]. Then the left term is not independent of x, and I guess we might get a [math]\dfrac{\partial p}{\partial x}[/math] term . My question is, how does the convective derivate (describing only change in the x-direction) relate to the viscosity term (describing only change (or actually acceleration of the speed) in the y-direction). I can understand that the closer we are the edge of the bay, the more the friciton affects the flow, and the smaller the change in the speed in the x-direction. What i dont "see", is how that follows from the balance in the NS-equation, and I'm hoping someone could nudge me in the right direction.
-
I am assuming [math]\dfrac{\partial}{\partial t}=0[/math], so [math]\dfrac{{\partial u}}{{\partial t}}=0[/math], and [math]\frac{{\partial p}}{{\partial t}}=0[/math], What I am not assuming is, that [math](u \cdot \nabla)u = u_x \dfrac{\partial u_x}{\partial x}=0[/math]. Assuming one layer (i.e. no z-direction), my NS simplifies to: [math]u_x \dfrac{\partial u_x}{\partial x} = \nu \dfrac{\partial^2 u_x}{\partial y^2}[/math] The question is, what is the connection between those terms? Is this equation even possible if I assume no [math]\nabla p = 0[/math]? Of course if we add the z-direction we have to add the hydrostatic pressure [math]\frac{{\partial p}}{{\partial z}}[/math] right? I will also need to account for the bottom friction and possible wind stress by adding a term [math]\nu \frac{{{\partial ^2}u_x}}{{\partial {z^2}}}[/math]. The question still stands: On the left I have no other terms then one describing the change in the x-direction [math]\frac{{\partial}}{{\partial x}}[/math]. What is the interpretation to get these balanced out with the terms consisting only of changes in the y- [math]\frac{{\partial}}{{\partial y}}[/math] and z- direction [math]\frac{{\partial}}{{\partial z}}[/math]?
-
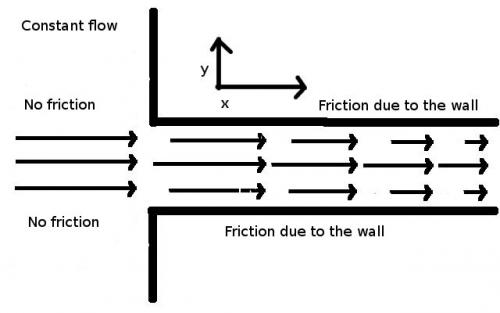
Consider a flow in a one layer, two dimensional tunnel/bay. Assume edges in the y-direction across the bay, but no edges in the x-direction of the flow. If we assume the velocity across the bay to be 0, and the situation to be stationary ([math]\dfrac{\partial}{\partial t} = 0 [/math]), the the left side simplifies to a one dimensional directional derivative [math]u_x \dfrac{\partial u_x}{\partial x}[/math]. Assuming constant pressure, then the right side simplifies to [math]\nu {\nabla}^2 u_x[/math]. We only have friction from the edges, so the viscosity term further reduces to [math]\nu \dfrac{\partial}{\partial y}(\dfrac{\partial u_x}{\partial y})[/math], or [math]\dfrac{1}{\rho}(\dfrac{\partial \tau_y}{\partial y})[/math], depending on how you want to write it. The question is: How can these be in balance, when on the left side there is no [math]\dfrac{\partial u_x}{\partial y}[/math] term, but on the right there is only a term dependant on [math]\dfrac{\partial u_x}{\partial y}[/math]? To make things clearer I left out the continuity equation, which means that we might have a sing at the "end" of the bay so we are not assuming [math]\dfrac{\partial u_x}{\partial x}=0[/math]. If we want [math]\nabla \cdot U = 0[/math], we can reconstruct the scenario by adding depth. Then the directional derivative will still not have any [math]\dfrac{\partial u_x}{\partial y}[/math] term, but the the viscosity term will. EDIT: This might fit better under Earth Scienses or Engineering. Sorry if it ended up in the wrong place.
-
This might be heading for an off-topic, but... I am sure many people would be happy to speculate, but you need an idea worth the speculation. In most of the presented ideas (or "theories"), this is just not the case. When an idea is presented, it is natural for anyone to try to shoot it down with easy arguments as a part of an "feeling out" process. If the original writer has convincing answers to present, then the thing might get interesting. In most cases it is painfully obvious that the idea is shot down by the first, very elementary arguments. Then there is really nothing left to speculate about.
-

Why (science) world is afraid of paradigm changes?
tmpst replied to illuusio's topic in Speculations
It is pretty obvious to me that you are confusing the scientific process with unwanted and unfounded resistance. -

Why (science) world is afraid of paradigm changes?
tmpst replied to illuusio's topic in Speculations
Did he present his work in 1992? It seems like the paper has been published in 2012, so where did you get the twenty years? And who has resisted his work? -
Yes. To pick an arbitrary point is not the same as to pick any specific point. You have to show continuity at a point, and the only thing you can assume about the point is that it is in the set (eg. [0,1]). The point of this is that when you have shown how the argument is done, then you can use the same argument for any specific point. In other words you have shown that the arguments works for all points in the set, thus the continuity of the function is proved.
-
Ah, but by picking an arbitrary number you are not showing that the function is continuous at a single point, you are showing that the function is continuous at every point in the set you picked your point from (think about it!). This, however, is just the definition of the function being continuous on the whole interval, because continuity is a property that is defined pointwise. If you want to show that the function is not continuous, you can of course just pick a specific point, and show that it is not continuous at that point. Observe that you (usually) can't pick an arbitrary point when doing this. You have to look at the function and try to figure out where is behaves "badly". Pick that point, and show that it is not continuous. Observe that then you have shown only that the function is not continuous at that specific point. We still don't know anything about the continuity of the function at any other point. This is still enough to show that the function is not continuous on any set containing that specific point, because (again) the continuity was defined pointwise.
-
You just have to prove that it is continuous for every [math]x \in [a,b][/math]. In the proof just pick an arbitrary number [math]x \in [a,b][/math] and show that the funktion [math]f[/math] is continuous at that point. Also if you know that the funktion [math]f: \mathbb{R} \rightarrow X[/math] is continuous, then the restriction [math]f_{\vert [a,b]}[/math] is automatically also continuous.
-
Ah, you'r right. Seems like I didn't think it through on the finite groups. I am familiar with homological algebra, so I will definitely look up the Ext functor. Thanks for your help!
-
This has kind of been bugging me fo a while. Let's say we have two groups and an isomorhism [math]\varphi: G_1 \cong G_2[/math]. If [math]H_1 \lhd G_1[/math] is a normal subgroup and we denote [math]H_2 = \varphi(H_1)[/math], then surely the quotient groups [math]G_1/H_1 \cong G_2/H_2[/math] are isomorphic as well. But what if we have a different isomophism [math]\theta: H_1 \cong H_3 \lhd G_2[/math]. Now we can't draw the conclusion that [math]G_1/H_1 \cong G_2/H_3[/math]. For example [math]\mathbb{Z} \cong \mathbb{Z}[/math] and [math]2\mathbb{Z}\cong 3\mathbb{Z}[/math], but clearly [math]\mathbb{Z}/2\mathbb{Z} \cong \mathbb{Z}_2 \ncong \mathbb{Z}_3 \cong \mathbb{Z}/3\mathbb{Z}[/math]. When can we substitute isomorphic groups when making quotient groups? If the groups are finite then nothing can conceivably can go wrong. But what about infinite groups?
-
Please read my first answer. By giving 0/0 the value 1, you are in face giving 0 the value 1. If you combine my two posts, you can see that I have shown that [math](\frac{0}{0}=1) \Rightarrow (0=1) \Rightarrow (\mathbb{R} = \lbrace 0 \rbrace)[/math]. If you can find a flaw in my deduction, please feel free to point it out. If not, then I am done.
-
I just did, because [math]1=0[/math] is a contradiction you can't solve. The number 1 has the property [math]x \cdot 1 = x[/math], and the number 0 has the property [math]x \cdot 0 = 0[/math] for all [math]x \in \mathbb{R}[/math]. If [math]0=1[/math] then [math]x = x \cdot 1 = x \cdot 0 = 0[/math] for all [math]x \in \mathbb{R}[/math]. From defining [math]\frac{0}{0} = 1[/math] it follows that there is only one real numbe, e.g. [math]\mathbb{R} = \lbrace 0 \rbrace[/math]. You can't make this work. (And now I gave it two shots...)
-
Ok, I'm only going to give this one shot. Suppose [math]\frac{0}{0} = 1[/math]. Because of the property of [math]0[/math] it follows that: [math]0 = 0 \cdot 1 = 0 \cdot \frac{0}{0} = \frac{0 \cdot 0}{0} = \frac{0}{0} = 1 [/math]. So by claiming that [math]\frac{0}{0} = 1[/math] you are actually claiming that [math]0 = 1[/math]. This is a contradiction, because we know that they have different properties in the ring of the real numbers, and as such they are unique. So if you want to keep the algebraic structure of the real numbers as a ring, then you can not claim that [math]\frac{0}{0} = 1[/math]. And if you are thinking in the lines of "Fine, I can live with losing the ring structure of the real numbers", then you are not really defining [math]\frac{0}{0}[/math] as we know the number [math]0[/math], because, well, you just lost the meaning of the number [math]0[/math], so you have nothing to define. Makes sense?