Gareth56
Senior Members-
Posts
279 -
Joined
-
Last visited
Retained
- Atom
Recent Profile Visitors
The recent visitors block is disabled and is not being shown to other users.
Gareth56's Achievements

Atom (5/13)
11
Reputation
-
Oh right. Even more confused now as to how someone/something can have Angular Momentum when moving in a straight line.
-
So if I've understand the above replies correctly the runner only posses L when they land on the edge of the rotating platform and not before. Therefore only the angular momentum of the platform should be considered in Lbefore. Thanks
-
Can someone setting a friendly argument? The conservation of angular momentum says the angular momentum of a system before must equal the angular momentum after. That is Lbefore = Lafter So, if a runner has linear momentum just before they jump onto a rotating circular platform does this have to be taken into account when calculating the Lbefore ? One argument is that the Lbefore only comprises the rotating circular platform because the runner who only has linear momentum hasn't landed on the platform and the Lafter should include the runners angular momentum using their l converted linear speed to angular speed and their Moment of Inertia at the edge of the rotating platform. So in essence the Lbefore = Lplatform and Lafter = Lplatform + Lrunner The alternative argument is that Lbefore = Lplatform + Lrunner and Lafter = Lplatform + runner I'm inclined to opt for the first argument because the only thing that has angular momentum before is the rotating platform, the runner doesn't have any angular momentum just linear momentum. It's only when they jump onto the platform do they then possess angular momentum. Sorry to be a tad long winded but if someone could adjudicate I'd be very grateful.
-
It's the definition that's given in my University Physics textbook!! However, many thanks for you patience and explantations. It's appreciated.
-
Isn't it the case that by definition mu = F(friction)/Normal Force and again by definition Normal Force = mg Therefore mu depends on the value of g.
-
If I could take what I've underlined. Again apologies for my dense understanding of this matter. You say that mu is a constant but if mu depends on the value of g (as we've established above) then given that g can vary e.g. g on the Earth > g on the Moon how can mu be classified as a constant? I agree that N is a variable because N varies with the value of g. Had mu been experimentally determined on the Moon would it have had a different value from that experimentally determined on the Earth? I appreciate your patience, but I will understand if you give up!
-
Hi Still a tad confused I'm afraid. If the Force (static friction) = μs N (and N = mg) then μs = Force (static friction)/ N = Force (static friction)/ mg However if the value of g is different then surely the value μs will be correspondingly different, same goes for μk. Sorry for coming across as thick on this but it really does confuse me as why the values should be the same on both the Earth and the Moon when μs and μk are dependent on the value of g from the equation μs = Force (static friction)/ N = Force (static friction)/ mg Thanks
-
I'm having some difficulty understanding why the coefficients of static and kinetic friction are constant e.g. they are the same on the Earth and the Moon. For example if μs = Friction Force/Normal Force then because the Normal Force is acceleration due to gravity dependent (mg) and the acceleration due to gravity on the Moon is less than that on Earth wouldn't this change the value of μs or μk, so they would be different on the Earth and the Moon? Here's the question that's causing my confusion;- A crate of 45.0 kg tools rests on a horizontal floor. You exert a gradually increasing horizontal push on it and observe that the crate just begins to move when your force exceeds 313N. After that you must reduce your push to 208N to keep it moving at a steady 25.0 cm/s. B.) What push must you exert to give it an acceleration of 1.10 m/s^2? © Suppose you were performing the same experiment on this crate but were doing it on the moon instead, where the acceleration due to gravity is 1.62m/s^2. (i) what magnitude push would cause it to move? (ii) What would its acceleration be if you maintained the push in part (b)? I would have thought that on Earth where g = 9.81m/s^2 to calculate μs & μk you would use 313 N = μs*m*g = μs*45kg*9.81m/s^2 μs = 313/(45*9.81) = 0.709 208 N = μk*45*9.81 μk = 208/(45*9.81) = 0.471 However on the Moon the value of g = 1.62m/s^2 making μs = 313/(45*1.62) = 5.33 and μk = 208/(45*1.62) = 2.85 However the answer leaves μs & μk the same on both the Earth and the Moon???? Thanks
-
So it's all about the electrons wanting to be in a lower energy state and it's easier in energetic terms for Na to give Cl its lone electron than for Na to be given and electron (as in a reduction reaction). Thank you John.
-
I thought I taken that into account above by saying that Na likes to combine with say Cl to form NaCl making NaCl (each atom has a full shell of electrons). However that does't explain why Na prefers to do this rather than exist as Na. That is because it's so easily oxidised why is Na so difficult to reduce. The OIL part is easy by the RIG is difficult!! I suppose it's a deeper question.
-
Can someone explain why if a metal is readily oxidized why the resulting ions or compounds are difficult to reduce? I understand why something like sodium wants to loose its lone 3s electron to form say NaCl but then can't associate this fact with the difficulty in obtaining Na metal. Is it because Na prefers to exist in nature as as ionic compound rather than exist as metallic Na? Thanks
-
Never mind, it's obviously a very challenging torque problem. By the way swansont the angle is 80deg!!! Thanks anyway.
-
Thanks for that. I think I understand now how the torque about the shark is taken. You drop a line down from the shark's weight to the base then calculate the lever arm. Torque shark = 10000 x 4 x sin 30. Where I'm having difficulty is seeing where the Tension Torque = T x 4 x sin 80 comes from. I'm lead to understand that it's the perpendicular component of the force that acts on the pivot point is the one that counts.
-
In the example below it's the length of the rod (4m) that is taken as the lever arm to calculate the torques around the top where the shark and tension rope is attached. Can I ask why? Because in a ladder against the wall [torque] problem the length of the ladder isn't taken as the lever arm it's the perpendicular distance from the pivot point (usually where the leader meets the ground) to a point on the ladder. Thanks.
-
Gareth56 started following Torque and lever arm query.
-
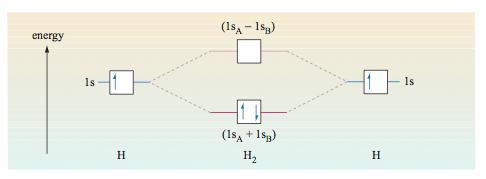
I read that an electron in a molecular anti-bonding orbital is at a higher energy compared to the atomic orbital than an electron in a bonding orbital however it does not explain why an electron in an anti-bonding orbital is at a higher energy. See attached image. Without going into advanced chemical principles could someone explain why this is the case? Thanks.