dalgoma

It has to be Meccano!

Assuming that the air in tyres is at 2 bars, you would be releasing twice the volume into the atmosphere and replacing it with CO2 would isolate quite a lot of CO2!

If all the tyres of all the vehicles in the world was replaced with CO2, what would it do for global warming?

A falling weight. And the power available need not necessarily cease when the weight reaches the end of its travel ... http://monologues.co.uk/004/Bricklayers_Story.htm

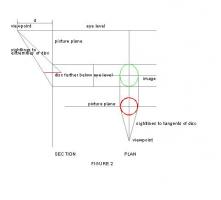
Regarding the disc viewed edge on:- Although the line has no width, it does have length - and that is information, not nothing. Viewed from the disc edge, the line is a tangent of infinite length. Unless viewed from infinity its length is always greater than the diameter of the disc. When viewed from infinity it is nothing.

Joining the 8 vertices of one cube on top of another has got a certain logic :- View a square to a corner you see 2 lines View a cube to an edge you see 2 squares View a 4D cube from a chosen location you see 2 cubes. By choosing the viewpoint we seem to be able to obscure a dimension.

4 D CUBES<BR style="mso-special-character: line-break"><BR style="mso-special-character: line-break"> To construct a cube, we join 2 squares together with 4 lines each the same length as the side of the square to each of the vertices. If we put one cube on top of another, we can join the 8 vertices with lines of the same length as the side of the cube. Is this a 4D cube? If not why not!

Wow, I like the link. But I don't think it is much to do with the focal length of the lens. Can we agree that, apart from the obvious grain, a photo taken with a long focus lens is indistinguishable from the centre of one taken with a wide angle lens at the same location. The only way to change the perspective is to move.

The following was written by Peter Hilton, Mathematician at Bletchley Park in 1943, one of the Emigma codebreakers. "Doc note, I dissent. A fast never prevents a fatness. I diet on cod" A coincidence- I have just noticed that Peter Hilton died on Dec. 2. http://www.guardian.co.uk/science/2010/dec/02/peter-hilton-obituary

Yes. And if you drilled a 1 metre long hole through the middle of a earth sized sphere, the volume left would be equal to that of a 1 metre diameter sphere without a hole.

I put the picture plane at the centre of the circle to make the maths easier when evolving the formula. This figure shows another circle as well as their surrounding squares - and yes indeed, the centres are at the intersection of the diagonals of the squares.

For Tony. Absolutely right! For Michel- The construction is my own and seems to me simple, have a certain mathematical elegance and satisfies observatioin. However, I cannot at the moment relate it to the projection of a particular circle at a particular location. What it does do is predict the tilt angle of an elliptical image whose centre P is in that position in relation to O whatever its size. Also I cannot establish major an minor axes. For instance, if we plot the image of concentric circles, They would not share the same common centre. Hence, they would have their own tilt angles if the were not on CoV. Can I suggest that you view CiP 2. This produces circular images! and they are generated by projection from plan and section in the traditional way. I would be interested in your comments.

Yes, I should have said "without so much loss of definition" Like the old days you chose a slow speed film for a fine grain if you wanted to enlarge. Ah, there is the rub! In all my constructions I have assumed a flat picture plane normal to the line of sight in both planes. Just like a camera that does not move.

Michel, Thank you very much for your input, I very much appreciate it. Is that what we call anamorphism? - Like the skull in Holbein's "The Ambassadors". If magnification does occur why does a raptor not use it? Merely focusing does not make things bigger, having more rods or whatever in its retina dosen't either - it just makes magnificatiion possible without loss of definition. As you know log. spirals are closely allied to the fibronacci series used so much in nature from the breeding cycle of rabbits to the arrangments of tree branches and dare I say, architecture, apporoaching the proportion 1:1.6180933... I posted to a falconry forum a received this reply - Great post ! I do not believe they see things at a distance as larger due to the fact of calibrating the distance to acquire the quarry. I have to agree that maybe in fact the eye Zooms in and out like the Lens theory. This has often fascinated myself. But also as I have hawked over many years and I have often wondered when you kick up a Rabbit and it does a wing over and crashes the brush after a snake ? I have certainly have seen some odd things while hunting with a BOP. Surley, the bird would not have seen the snake if it was solely focused on the rabbit. We may have exhusted this subject. I only raised it when looking at the views of Circles in Perspective. It is fun though! .

no we don't! see for example http://www.math.utah.edu/~treiberg/Perspect/Perspect.htm#circle

For Michel - Thanks for reply. If you move towards an object looking at him sideways, your path will be a logarithmic spiral. I guess that's what the "behavioural studies" tend to show. But if a bird looks sideways, it is probably to avoid the phenomena described by dalgoma, not to use it as a magnifying trick. Log. spiral only if the line of sight is maintained with respect to the axis of the bird in flight. Which is a pretty good definition of a log spiral. - the tangent to the curve making the same angle with respect to the origin.

For Michel - Your construction of the central axes of the cups, rightly going to a vanishing point, confirms that they are not at right angles to the major axes of the elliptical images of their rims. I contend that my contruction provides a more accurate result for the tilt. for Tony - The link shows the traditional rough & ready method of constructing the image. How does the circle know that it is surrounded by a square? My post (CiP) I think, supplies the answer without recourse to circumscriptions. Thank you all for your interest.

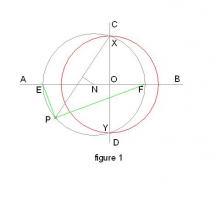
CIRCLES IN PERSPECTIVE 3 When you are not looking at them! When we view the rim of a cup on a table directly in front of us, the major axis of the elliptical image we see is always horizontal from whatever angle we view it. However, it does tilt if the cup is positioned to left or right of our centre of vision. Here is a way to establish that tilt angle. On essentially a picture plane - a. Draw a horizontal line AB representing eye level and the vertical centre line of vision CD intersecting at O. b. Describe a "boundary" circle radius d centred on O intersecting CD at X and Y. "d" is equivalent to the distance of the viewpoint in front of this picture plane and is that self same circle as the "bubble" circle used in CiP2 to generate those truly circular images. c. Now pick a point P that is the centre of an elliptical image. d. Join PX (or PY) and construct its perpendicular bisector to meet AB at N. e. Describe a circle centre N and radius PN intersecting AB at E and F. f. Join PE and PF. These are the axes of an elliptical image centred on P viewed from distance d. Note that for a series of locations for point P on a horizontal line, the tilt goes from zero at CoV, to a maximum at the boundary circle, gradually returning to zero again at infinity!

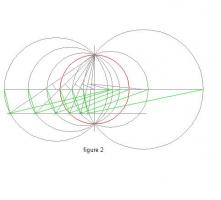
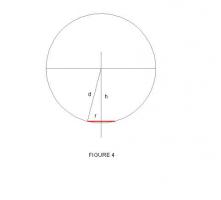
Circular Circles in Perspective We know that a circle in perspective is an ellipse. Here is the traditional method of constructing such a view. With a viewpoint a horizontal distance d from the centre of a target circle of radius r (Fig 1) The eye (camera) is horizontal and viewing a target circle on a horizontal surface directly in front but a vertical dimension h below eye level The resultant image is – an ellipse. If however the circle is further below, using the same construction, the image rotates 90 degrees. (Fig 2) Could there be therefore, a location for the target circle where the image is a true circle? Consider that your eye (camera) is located on the circumference of a circular "bubble" of diameter d. The target circle of radius r settles in the bowl of the bubble. (Fig 3) Distance h is therefore sq rt (d^2 – r^2) (Fig 4) The resultant image is a true circle and its radius is dependant upon radius of the target circle r, viewing distance d and viewing height h being Pythagorean. It follows then that if you stand say 354 mm back from the edge of a circular pool of 3 metres radius and take a photo of the opposite bank with camera horizontal, 1500 mm above the water. The image of the opposite bank will be the arc of a true circle!

Here is a way of visualising what is going on. Imagine one of those flat circular lollipops and hold it directly in front of you, then lean it away from you at say 8 degrees. Now spin the stick in your fingers so that the lollipop rotates 360 degrees. The effect will be seen by clicking on the attachment which has been constructed by animating 18 frames with a rotation interval of 10 degrees, using the method as previously described. OK I know it wobbles a bit. The stick that is embedded in the lollipop (albeit foreshortened) remains the same length throughout the rotation, it also remains vertical and becomes the common chord to all the ellipses. As I know the length of the axes of each I can locate their centres, calculate eccentricities and hence foci. That is what those dancing spots are...* *See what I have done there? Those three dots are also called ellipses!

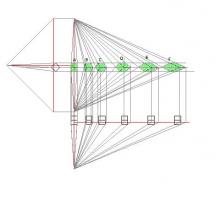
This is a perspective projection of a cube at various positions from the line of sight. It will be seen that the footprint of each image gets progressively larger the further to the right it becomes and in this instance the further away it is. This is against all common sense. Objects are supposed to get smaller as they get further away! Just suppose though, that this is true and the construction is valid, we could not possibly discern it. Just try reading a line of text when you are concentrating on the one above. Hawks however have a reputed 270 degree angle of vision. Is it possible that they use this phenomenon to magnify their prey when they stoop? If I look through a pair of binoculars I would not be safe moving around, I would bump into things. And raptores do it travelling at 100mph in 3 dimensional space! However, if they looked straight ahead but "took in the view" of their prey at, to them a constant optimum angle, they would need to fly in a curve to maintain it. I am informed by falconers that hawks do indeed stoop in a curve and it has been established that this curve is a logarithmic spiral. Could this be a reason?

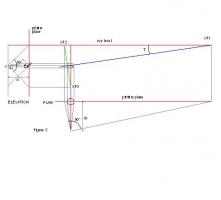
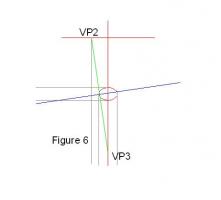
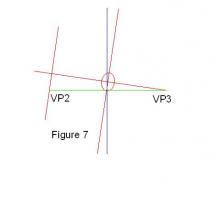
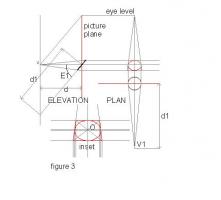
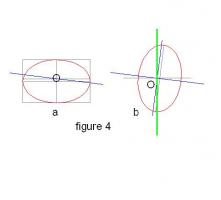
"The puck stops here". Misread in the Oval Office. Eye Level Figure 5 shows the setup that created the ellipse in figure 4a. Using inclination E1 and distance on plan d1. 1 We just have to add the tilt angle T (the blue line) and extend it to meet eye level at VP1. 2 Use this to orientate a square on the plan that would generate this VP from viewpoint V1. 3 Hence position VP2 from the right angle to this line. 4 Similarly, locate VP3 by drawing the line at right angles to the inclination (E1) on elevation. 5 Now connect VP2 and VP3 with a straight line. The result is shown at Figure 6 Now rotate the whole so that the blue tilt line is vertical. (Figure 7) It will be seen that the tilt line has become the centre of vision and the line joining VP1 and VP2 has become the eye level! Finally superimpose the construction on the view from upon Westminster Bridge ... "Earth has not anything to show more fair, Dull would he be of soul who could pass by, A sight so touching in its majesty"

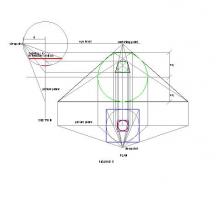
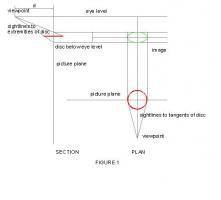
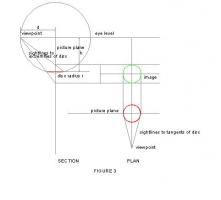
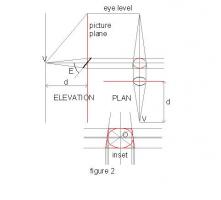
"Heed thy ellipse, note two axes" misheard in the Oval Office. Major and minor axes. The one time we can be sure that we are creating the right image of a circle in perspective is when the major axis is horizontal and we are looking directly at its centre as in the case of the cup on the table in front of us. Draw the side view of the setup viewing the disc edge on from the viewpoint V, at angle E and distance d. The picture plane, where the image is projected, can be at any anywhere but we know it is always at right angles to the line of sight. Eye level is established by drawing a line from viewpoint V, parallel to the disc to meet the picture plane. We can now draw sightlines from V to the extremities of the disc and extend to the picture plane as necessary. Horizontals from these two points will determine the top and bottom of the image – the MINOR AXIS. Looking directly down on the disc we know that it will appear to be foreshortened to an Ellipse. The major axis of it will be its diameter 2*r. The minor axis will be cos(E1)*2*r Place the plan at right angles and again draw sightlines from V, this time to the tangents of the ellipse. Again extend to the picture plane and project vertically. The distance apart of these lines will be the MAJOR AXIS of the perceived image. The elliptical image can now be drawn. See Figure 2 But there is an easier way (figure 3) The side elevation is as figure 2 but for the plan, we draw a circle of radius r centred on O. And compensate by moving V to V1 a distance d1 = d/cos(E) Sightlines are projected in the same way and the resultant image is exactly the same It makes the maths a lot easier! See Figure 3 Now we can return to the image of the London Eye. We proceed as figure 3, but instead of angle E, we use angle E1 (figure 1) for the inclination. It only remains to transfer angle T (figure 1) to the image passing through O and rotate to obtain the required tilt and add the centre of vision through O. See Figure 4

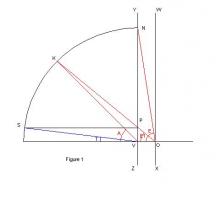
Here is a way to establish what that "funny angle" is. Naturally it all depends on the location of the viewpoint. I took the picture of The London Eye from the north end of Westminster Bridge, the camera was inclined at about 8 degrees. I estimate that the distance to the centre of the wheel to be 400 metres and the angle to the plane of it approx. 45 degrees. I know that The London eye is 62.5 metres radius. Hence d (for distance) = 400 A (for Azimuth) = 45 degrees E (for Elevation) = 82 degrees (90-8) r (for radius) = 62.5 Referring to Figure 1 1 Draw verticals WX and YZ any distance apart, together with horizontal baseline intersecting the verticals at O and V 2 Draw line at angle E from O to meet YZ at N 3 Describe arc centred on V and radius VN 4 Draw line at angle A from V to meet arc at K 5 Join OK and label point P where it intersects with YZ, and label angle KOV, E1 6 Draw horizontal from P to meet arc at S 7 Join SV. THIS IS THE REQUIRED TILT ANGLE T Distance d and radius r have no bearing on the tilt angle, as long as d is not zero. Angle E1 is required to establish the ratio of major to minor axis and thence show that the approach is a correct one. That is if anybody is interested.

Have you noticed that when you look at a clock on the wall above you, the axis of the perceived elliptical image is at a "funny angle" and it moves when you move, yet the major axis of the rim of a cup on a table in front of you is always horizontal - and you cannot move to a position where it is not so. Why?