h4tt3n

Hello all, Here's an update on the iron slab. These photos were taken one month ago: And these photos were taken today: As you can see, there is practically no change. Still no rust. There's also still non-corroded metal on the surface, although the areas with shiny metal seems to shrink very slowly. Salt has been added regularly to keep water salinity high in the container. Cheers, Mike

Hi Enthalpy, Yes, that is perfectly true. As far as I know, this is in fact one of the method used by archaeometallurgists. The thing is, prehistoric and medieval iron - having never been molten - often contains many layers of different iron alloys. Knives and axes were deliberately forged in soft iron, and then a piece of hard steel or phosphorus iron were welded into the edge. Also, old tools and weapons were recycled again and again, so that f.inst. inside an axe you may find the remains of an older sword or other artefact of importance. The point is, you can't just do one surface analysis and then conclude that the entire artefact is of that particular alloy. You would risk to lose invaluable information about the history of the object and the process of crafting it. Therefore, artefacts are usually cut up, and then both microscopic and evaporative analysis is done on each layer - both metal and slag inclusions - is done seperately. But apart from that, for modern, completely homogenous steel, the method you describe would be perfectly fine

Hi Studiot, Indeed this method is very similar to the (many different) ones used in Britain and northern Europe throughout the iron age. Formally, the iron lump made in this process is called a bloom, whereas ingot refers to something than has been molten. Liquid cast iron or pig iron is a result of the "modern" direct iron production method and was unknown in European prehistoric times. Bloomery iron has not been liquid at any time and is very, very different from cast iron. Bloomery iron is usually very heterogene, consisting of ferrite crystals of very different size with quite a lot of slag inclusions in it. I'll look into this Blackdown place, sounds interesting. Maybe we could do a smelt together someday Cheers, Mike Hi Enthalpy, Carbon content is a difficult one. We know that quenched, tempered steel was used in northern Europe deliberately sometime in the middle iron age onwards, but the process wasn't common everywhere before early middle ages. Unfortunately, the preservation process used on iron artefacts include heating the object to a glowing red, thereby forever erasing any detail about how the metal was treated. Also measuring the carbon content of an artefact is a destructive process, since you need to cut out a piece, grind it and do microscopy on it. So it's not done as often as one could wish for. In the iron age there were other ways to make a knife hard than by using steel. One is by using phosphoric iron, which gets very hard and brittle, similar to carbon steel, but harder to work with. Phosporus is very common in bog iron ore, and all the iron I have ever made contains phosporus. Another way is to cold-hammer the edge of a soft iron knife. This deforms the structure of the iron and makes it harder and more brittle. This is used both for thinning and sharpening, and was commonly used on schythes up until about 60 years ago. So, long story short, I simply don't know the carbon content of the knife, it was never analysed, but it is very likely that there isn't any carbon in it. Cheers, Mike

I think it's about time I explain the process in a bit more detail. In the attached pictures you can see the process from raw ore to finished object. First, the bog iron ore is dug out of the ground. It has a very rusty color, ranging from greyish black over brown to yellowish red. The ore is roasted on a fire to make it porose, and is then crushed to a fine powder. The crushed ore is put into a smelter with charcoal, usually in a 1 / 1 ratio. Air is blown into the bottom of the smelter to increase temperature. Usually, the smelter is about 700-800 degrees celsius in the top (glowing a dull red) and 1200 - 1300 degrees in the bottom (glowing an incandescent yellowish white). Iron oxide is reduced to metallic iron by carbon monoxide, and the remains of the ore is molten into an iron-rich slag, which protects the iron from re-oxidation and taking up too much carbon. When the slag has filled up the bottom of the smelter, it is tapped from the furnace so it won't clog up the air inlet. Please note that the iron does not melt. At no point in the process from ore to tool is the iron liquid. Once the so-called bloom has grown big enough, the process is stopped and the iron extracted from the smelter. The bloom is then usually forged on a large rock by 2-3 people with sledge hammers. This consolidates the iron, removes excess slag, and shapes the iron so it's easier to work with. Finally, the bloom is cut into two or three "klimps" each weighing 1-2 kilograms. Finally, the klimps are heated in the forge and worked into bars, tools, or weapons. Cheers, Mike

Hi Enthalpy, With the iron-age process it is indeed possible to produce very low-carbon iron - almost pure ferrite. So that's a possibility, yes. I don't know about precipitation of carbon in iron - will have to investigate on that one. I know of the properties of steel with silicon, but generally these alloys aren't forged for the very reason you mention. I have seen several analyses of both pre-historic iron and modern iron made with prehistoric methods, and I've never seen any trace of silica in them. The metal often contains silicates in the form of slag, but that's an entirely different story. There simply isn't heat enough in the smelter (800-1300 degrees celsius) to reduce silicates into free metallic silica. In the museum where I work as a blacksmith there's an iron age knife on display with the exact same smooth black surface as the iron slab in the photos. No thrace of rust or corrosion, nothing's missing, it's just shiny black. It's from the first centuries AD, making it at least 1800 years old. When I first saw it I thought it was bronze, which in the right conditions can be perfectly preserved. When I talked to the archaeologer supervising the dig, he told me that it was indeed iron, and that he was as baffled about it's extremely fine condition as I was. Things like these just pokes my curiosity!

Hello again, Now it's been more than an month since I started this post. In the mean time the iron slab has been lying in a bucket of salt water in the garden, fully exposed to wind and weather. As you can see in the images, there is still no sign of rust. Most of the surface is covered in a thin, black film that can be rubbed off with a cloth. As before, a considerable part of the iron is still shining like fresh polished silver, with no sign of rust, oxidation or corrosion of any kind. I still haven't found any satisfying explanation to the phenomenon. Cheers & merry christmas, Mike

Hello everyone, Will try to answer some of the questions that have come up... @Moontanman Yes, it is quite probable that this iron contains phosporus. There is often quite a lot of Phosphates in the ore, 1-10% is not uncommon. So, the anti-rust mechanism we see here may be the same as in the Delhi Pillar. What makes this interesting is that I know how to produce the material. @Endy0816 Raw iron bloom contains some silicates that come from the ore, but I don't think they play a large role here. The slag is very brittle and porose, and it doesn't cover the iron particles. If they did, I wouldn't be able to forge it. Been there, done that - when the metal is hot, it's like trying to forge porridge. @Enthalpy Hi there, and thanks! I know for sure that this iron contains absolutely no silica, nickel, cobalt, or chromium - not even the slightest trace. Also no manganese, although this metal is abundantly present in the local ore. The smelting process is happening at such low temperatures, 800-1300 degrees celsius, that other metals cannot be smelted. And yes, it is very ferromagnetic - it's almost pure ferrite. The explanation of the anti-rust mechanism must be somewhere else. Cheers, Mike

Hello John, Well okay, considering that my "laboratory" consists of a grass field with clay furnaces, and ill defined bog ore - and no measuring equipment whatsoever - my understanding of the term "pure" may differ a bit from that of a scientist, I'll grant you as much. Having said that, I think you might be surprised how pure the iron made in this process actually is according to analyses. As a blacksmith I have come to prefer the home made iron over at least some of the cheaper irons available on the market. It is more ductile, easier to forge weld, and can withstand beeing worked at both lower and higher temperatures than off-the-shelf bar iron from the local hardware store. Of course, none of this matters if you are just going to electro-weld it into a grid and cast it into a concrete element, but it matters if you intend to really work with the material. Among fellow blacksmiths it is a common saying about iron and steel that the older it is, the better the quality. As far as I know, this is mainly due to the ever-increasing amount of poorly sorted scrap beeing meltet into virgin iron before shipping. That's good for the environment, but bad for steel quality. It cracks and breaks easily upon forging, and melts or burns easily upon heating. I have often seen - and heard from other blacksmiths - how chunks of un-molten high-alloy steel appears inside raw steel bars, ruining both the tools used and the project at hand. So again, which material is the purer one? As for the lack of rust, I think your theory about anodic protection might at least in part explain what is going on. At least when it comes to the salt water experiment because of the presence of a good electrolyte. Still, does this explain how it didn't rust while laying outside for six months directly exposed to the weather? Rain water is a poor conductor of electricity, and thus a poor electrolyte. Also, the iron slab was often moistened by rain, but never submerged (we get a lot of rain, but not that much). I know for a fact that this metal does not contain even the slightest trace of chromium, so it has to be something else. I'm meeting with some colleagues this weekend, mostly smiths and archaeologers, to do some more experiments. I'll see if I can get one of them to do an analysis of the metal, aiming specifically for an explanation why it resists corrosion. Cheers, Mike

Hello, I would like to show you this interesting phenomenton I came across by pure chance. The attached photos show a slab of pure iron that I have made from bog iron ore in a clay furnace, exactly like iron was made several thousand years ago in the european iron age. The slab is approx. 21 cm (8.3 in) wide and 6 cm (2.4 in) high and has been cut out of a larger bloom weighing about 7.5 kg (16.5 lbs) with an angle grinder. I have had it lying outside the entire summer in an iron age heritage center as part of a display on prehistoric ironsmelting. Now, after some time I noticed that the iron slab did not rust, even though we've had quite a bit of rain. Parts of the slab remained fresh and shiny as the day I cut it. Out of curiosity I threw it in a wooden tub of water, where it stayed for several days, still with no sign of rust. Finally I threw it in salt water roughly as salty as sea water to force start rust formation. As you can see in the photos, it didn't work. Just prior to capturing these photos I've taken the slab out of the salt water and gently brushed it over with a soft cloth, nothing more. Parts of the iron slab still shines with a silvery shimmer, completely unaffected by the corrosive environment. The rest is covered with a thin, dark brown to black film that can easily be rubbed away. The reddish brown sections is iron silicate slag that got stuck inside the bloom during its formation in the furnace. Could someone here please explain how come this particular block of iron does not rust? Mind you, as opposed to stainless steel this is very pure iron without any alloy elements, except perhaps for a little bit of phosphorus and/or carbon. Also, doesn't this have some interesting application possibilities in the field of engineering? Thanks in advance, Mike

@Swansont. Yes I noticed this when repeating the soot-in-water mirror experiment last night. The effect was much better when looking along a line near-parallel to the soot-covered surface than when looking along a perpendicular line. I don't think the soot method will work, but I need to do a few more experiments to be sure. Also, you have a very good point in mentioning that reflective materials are so because of their conductivity, which explains why a non-metallic mirror is difficult to make. Also, wouldn't it be possible to make a perfect mirror with a huge prism? Imagine it is shaped as a right angled isosceles triangle (correct term?) and you look into it through the side opposite to the right angle. I even think this prism would reflect the image correctly, and not "mirror" it. Here's an image: Cheers, Mike

Well, it's complicated. First of all, I am an old-fashioned blacksmith, and I even smelt my own iron viking age style, in a clay furnace. Metal - and especially iron and steel - is my life. I litteraly think in metal. I supposed this has backfired and made me very interested in how to make everyday tools without using metal. Also, a few years back I read a very fascinating sci-fi short story about a society that had no access to metal and thus had to come up with all sorts of alternatives, like bone, cheramics, glass, and so on. I don't know if it makes any sense or if you think I'm weird. I have just found it a very thought provoking mental practice to not think in metal

John, I want to make a metal-free mirror because metals are not available to me ;-) Stringjunkie & Moontanman - sorry, that won't work for me, but nice tries!

Thanks, both of you. These mirrors do seem to be used for very specialized tasks and require expensive equipment to make. Do you know if it is possible to make a typical bathroom mirror of more every-day materials (except metals)? For instance, I remember a "trick" where you can make any object shine like polished metal by first covering it with soot by holdig it into the flame of a candle and then lower it into a glass of water. Surely it must be possible to make a mirrior using similar techniques.

Hello folks, Does anyone here know a method to make a mirror entirely without the use of metals? Cheers, Mike

Nolan, try google "metallic glass" or "amorphous metal". That's probably the closest we get to UFO-metal or adamantium or whatever you want to call this stuff. In short, metallic glasses can be just about any metal or combination of metals and non-metals that have been cooled down so fast that it didn't have time to crystallize. The "glass" part simply means that it is amorphous, ie. without crystal structure (it doesn't mean you can see through it). Metals without crystal structure are *extremely* tough, but tecnically speaking they are not necessarily hard. This means you can deform them a lot without building up tension and breaking it. When "regular" metals deform, the tiny metal crystals slip on each others surfaces, or the usually well aligned atoms inside the crystals shift along different planes. More possiple slip planes means you can deform it more easily without braking it. Now, amorphous metal does not have any structure at all. The atoms are placed in a non-repeating random pattern. That's why metallic glasses are very very difficult to deform compared to "regular" metal. The problem is, these metallic glasses are very hard to make in large quantities, because you can't cool it fast enough. Metallic glass made in labs is usually very thin sheets of alloy sprayed or shot onto very cold surfaces. A few links to articles: http://link.springer.com/search?query=metallic+glass&showAll=false http://link.springer.com/search?query=amorphous+metal&showAll=false Hope this helps! Cheers, Mike

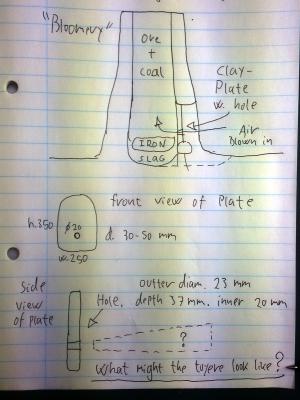
Enthalpy, thank you very much for your reply. You have given me some very tangible answers that I can work with. I'm not quite sure what you mean by "slowly convergent taper". Are you suggesting a tube that narrows in a lot at the far end and gets closer to beeing cylindrical at the near end? As you mention, the purpose of the tuyere is getting a relatively small volume of air / time moving as fast as absolutely possible. Slower air means more uneven furnace combustion, which again means worse result. In my experience, faster moving air also always implicitely means a more even air distribution across the furnace bottom. So, in that respect my question might be reformulated into: "How do you make a given volume of air / time move as fast as possible through a tapering hole approx. 20-30 mm in diameter?" When running at its best the furnace consumes 0.30-0.40 g charcoal / minute / cm2 furnace area. With a diameter of 25 cm the furnace thus consumes 150-170 g of charcoal per minute. This may give you an idea of the air volume / time needed. And yes, among other languages I read german. Will look for the Sigloch book. I've attached an image where you can see the size and shape of the original air inlets. Cheers, Mike

Thanks for your replies, both of you. I can see that I haven't quite explained the process well enough. I've attached an image showing the furnace. First, bone is a clear no-go, partly because it's much easier to make a tube of other materials like clay or metals like iron and copper. Secondly because of the phosphorus content, as Enthalpy mentions. P is a huge problem because it is also in the ore and results in large-grained brittle iron. Second, the iron is not liquid. It never melts but consolidates into a lump of solid iron just below the air inlet. The liquid slag flows into the bottom of the furnace, so you don't have to "blow through" either. The only obstruction for the air beam is charcoal sized like small rock or gravel and powdered ore as fine as sand. Third, the air is not blown into the furnace by blowing with your mouth into the tube. I am using hand operated double bellows or (mostly) a lab-grade electric blower. I am trying to understand what correlation there is between the shape and size of a tuyere and the air beam produced by it at a given air velocity / pressure. For instance if we have a conic tube that is 35 mm at one end and 20 mm at the other, you would still get very different air beams if the tuyere was 600 mm long or just 100 mm long. What is the optimal angle at which the tuyere narrows in? What is the optimal diameter in each end? What is the optimal length? I need some mathematical tools to work with this problem. I know about the Venturi effect and Bernoulli's law, but i feel I'm still missing a few pieces to complete the puzzle. Cheers, Mike

Hello, I'm hoping someone here might be able to shed some light on a prehistoric engineering problem that I am struggling with: I'm working with the reconstruction of prehistoric iron smelting techniques. In short, what I do is build a clay furnace and fill it with various amounts of charcoal and iron ore while blowing air into it at the bottom. Coal and ore is transformed into solid iron that stays inside the furnace and liquid slag that runs out of the furnace. When the smelt is over, I pull out the iron and forge it into bars on a large rock. The furnaces are roughtly 30 cm in diameter and 70-100 cm high. One of the major problems is getting the furnace content to burn evenly despite the fact that there is only blown air into the furnace through one small hole. Many different setups have been tried with various results. Very recently a bit of interesting iron age furnace slag has been excavated in Denmark. It seems to be a exact cast of the hole through which air was forced into the furnace. Liquid slag simply ran out of the hole and solidified in situ, preserving the shape of the hole to this day. The slag is a conic section with a length of 37 mm. the diameter in one end is 20 mm, and the diameter in the other end is 23 mm. Several other similar slags have been found, although less well preserved. The diameter of these varied between 20 and 30 mm. I am assuming that the bigger end of the hole was on the outside of the furnace and the smaller end was inside. So, here comes the questions: (1) Based on the above described hole size and shape, what would be the optimal tuyere size and shape if you want to force air all the way to the back of the furnace, 30 cm behind the hole? (2) Based on the above, what approximate air pressure / volume per time / velocity is this air inlet designed to work with? If my description of the problem seems unclear, then I can upload some photos or drawings of the setup. Thanks in advance, Mike

In the article both m and t seem to represent a tangent which defines the shape of the spline, but what is the difference between them? In the data set, (tk, Pk) for k = 1,...,n, does tk represent a set of arbitrarily chosen tangent vectors? Cheers, Mike

Thanks for replying, DrRocket First, a few words from the heart of a frustrated person trying to grasp a new field of math: While probably beeing perfectly clear to someone already understanding the concepts of the article, I hope you understand that it may still be unclear to someone still in the process of trying to understand them - which probably includes a good part of the people reading this article. I've seen this too often - the author of an article assumes the reader to know as much or nearly as much about the article topic as he does himself and therefore doesn't see the importance of explaining the used notation or the meaning of used variables, and wether they represent scalars, vectors, matrices and so on. I think this is one mayor reason so many people find math a hard nut to crack, as it can make simple concepts look more difficult than they are. Please have this in mind. And back on topic again: What I still don't understand is this: In the first equation, t is used as a unit interval defining how close the spline point defined by function P(t) is to either of the end points P0 and P1. If t = 0 then P(t) = p0, if t = 1 then p(t) = p1. So, if you want to do a smooth interpolation of p0 and p1 by calculating the - say - 9 equally spaced points on the Hermite spline laying between p0 and p1, you solve p(t) for t = 1/10, ... 9/10. Further down, the article mentions a data set (tk, pk), and this is what's confusing me. Here, t appears to represent something else or beeing used in a different way. The tk values are used to calculate the tangents in different ways - finite difference, cardinal spline, and Catmull-Rom spline. But what exactly are they and how are they calculated? Cheers, Mike

Hello, While learning about splines I've run into some confusion about the wikipedia article on cubic hermite splines: http://en.wikipedia.org/wiki/Cubic_Hermite_spline A few lines from the top of the article it reads: "The subinterval (xk,xk + 1) is normalized to (0,1) via t = (x − xk) / (xk + 1 − xk)." This is causing me some trouble. What does the "x" represent in the (x - xk) term? Also, if xk and xk+1 are vectors, then what does the division mean, since dividing two vectors is undefined? Is the t value a scalar or vector? In the article t seems to be used as a scalar term between (0, 1) which defines where the interpolated point on the spline is relative to the endpoints. A few pages down (Interpolating a data set) it says: "A data set (tk, pk) for k = 1, ..., n (...)" Here t seems to represent something different than the t in the equations in the first part of the article. What does the tk part of the data set represent? tangent vectors or scalar t values? I would appreciate if someone could clarify this a bit. Cheers, Mike

Tin foil hat alert!

After implementing a number of more or less sophisticated iterators, the Newton-Raphson and Halley's have clearly come out on top. Especially when using Danby's initial guess E = M + ( sign(M) - (M / Pi) ) * (e/2). I find it interesting that both methods are of considerable age. So far I think I'll stick to these, but sooner or later I'll have to look at the bisection method as well, thanks for describing it in such a straight-forward way. Also, I couldn't help making a little experiment. I made an orbit simulation which is a sort of intermediate between Kepler's and Newton's ways. I describe the movement on the orbiting body with angular velocity and calculate movement based on conservation of angular momentum. Angular velocity is a function of distance, since w = L/m*r^2, where w is angular velocity, L is constant angular momentum, m is orbiting body mass, and r is distance. True anomaly at time T is simply found by integrating with time: v(t+1) = v(t) + w(t) * dt, where v is true anomaly, and dt is delta time. The new distance can be found from v, since r = a*(1-e^2/1+e*cos v), where a is semimajor axis, and e is eccentricity. Finally, the cartesian position can be found from distance and angle. Although very simple and computationally cheap, this method conserves energy and momentum perfectly and prevents the orbit from "drifting" off like other simulations based on integration algorithms. I think it has some potential, but it can probably be improved and there may be some undiscovered issues. cheers, Mike

This is really a form of perpetuum mobile. I remember spending hours and hours as a kid designing stuff like this

Ok, I gave it a try. For the following values: E0 = 0, eccentricity <= 0.99999, M <= 1.99999*pi, the iterator converges at a value of E < 2*pi, but it goes haywire beyond that. For E0 = M, on the other hand, it behaves perfectly for the highest values possible with double precision variables and converges in <= 34 iterations. I'd say this is as much a lesson in the importance of picking the right starting value as in the limits of the iterator. Yes, I noticed strange behaviour with values of M > 2*pi, got that fixed. Please help me understand this right. If if the sign of En+1 is different from En or En+1 > pi, then I should throw away the value of En+1 and continue iterating from En with the fixed point iterative method En+1 = M + e * sin(En)? Am I supposed to continue using the slower iterator until it converges or switch back to Newton-Raphson when the above conditions are met? Cheers, Mike