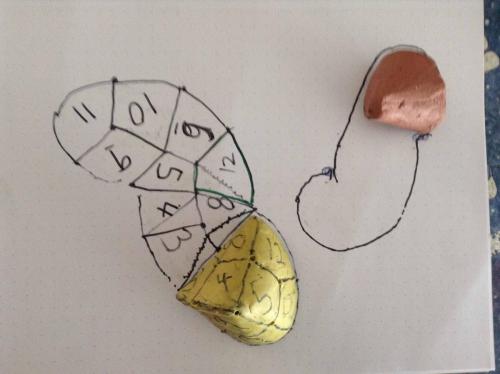Everything posted by tar
-
Dividing a sphere into twelve "identical" shapes.
I cut out the drawing in #114, leaving the shaded parts in, and if folded at the four points into 4 equal sections, you can tape the thing easily together as a tetrahedron, and see how the hexagonal planes are exactly intact. If you have a printer handy and a scissors and some scotch tape, its easy to do. 'course when I did it I redid the color and arrow directions as per the correct one. Perhaps I will repost that good one, without the pink Januses on it, for cutout purposes. Have something else to try that I might add as well, later. Actually, I already did the 3 point in the center in #113 "outside looking in" which you could printout and cutout and tape into a tetrahedron as well. So I don't need to do that again, except for shading the open part of the shields.
-
Dividing a sphere into twelve "identical" shapes.
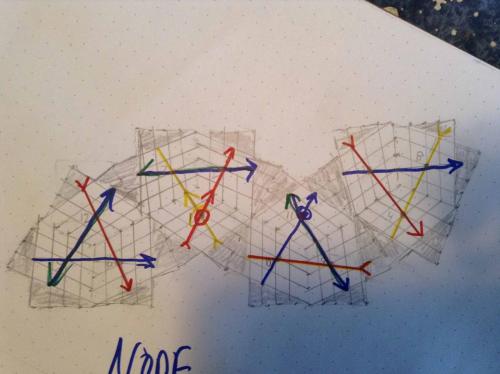
Thread, Cut a sphere up into the twelve sections (Januses) and laid them next to a proper drawing of the shaded open shields, with the arrows the right color and going the right direction. Interesting is that the surfaces of the Januses "fit" on the unshaded parts. Fit, when you "roll" them on the shape. It does not look it, but if you take a Janus and put it against the page at one end of an unshaded diamond and roll it to the other corner it gets there perfectly (or at least what looks close enough to be actual.) Same if you roll it from 120 to 120 degree corner. And the length of the edge of the unshaded diamond is 59 and the radius of the sphere is 59 so it seems that the unshaded parts should actually be the same area as the surface of the sphere (maybe.) Regards. TAR The twelve pink peices make up a sphere the same size as the green one shown whole.
-
Dividing a sphere into twelve "identical" shapes.
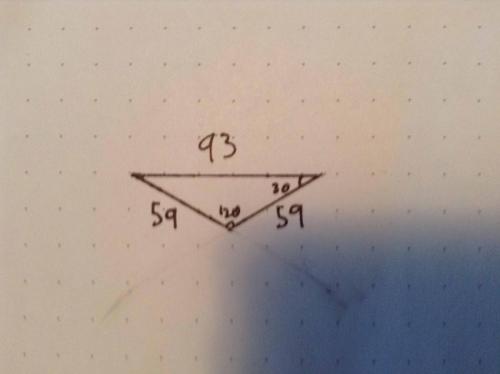
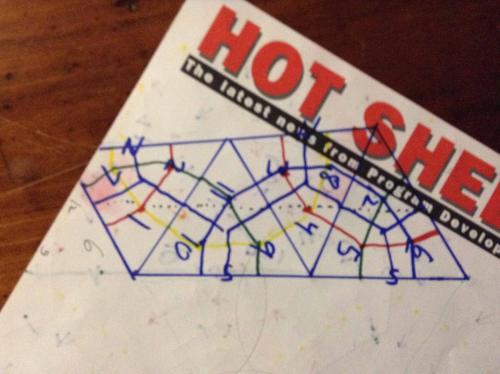
Thread, The open shield arrangement is good because it shows you where you cannot place a diamond, because it would overlap another on the sphere. In the 2d renditions of the sphere given by the equilateral triangle, the sides of the large triangle actually fold in half to touch themselfves around a three point. The use of the open shields shows where you cannot physically fit a fourth diamond because three 120 degree angles is all the three point has to offer. Anyway, ignore the color mistakes I made in the arrows, and check out how things look when you grey out the "unused" portions of the shields. (Not really unused because they show where the diamonds touch the next diamond on the sphere.) Also, I found this interesting triangle on the "Outside Looking Toward center" (posted yesterday) depiction using the "open shields" Look at the triangle below the red 4. It has a little r in it. It has these characteristics. The raidus of the sphere I am depicting is 59 (sixtiests of a inch) the diameter is 118, the circumference is 371 and 1/4C would be 93. The equator exactly bisects the 4 equatorial diamonds, so the length of the long axis of the diamond, on the surface of the sphere, should be 93. This also is what I measure on the depiction (although there might be a little confirmation bias, my lines being thick and slightly inaccurately angled). So, two interesting points. These 30 60 90 triangles can be found in the same places on both the 2D depiction and the 3D sphere, and in both cases are exactly 30 120 30 (two 30 60 90 triangles). Do not know yet what that means, in terms of where the depiction is accurate and where it deviates, but it is interesting to note that 93 divided by 59 is 1.58. Double this is 3.16 which is in the neighborhood of Pi. Regards, TAR
-
Dividing a sphere into twelve "identical" shapes.
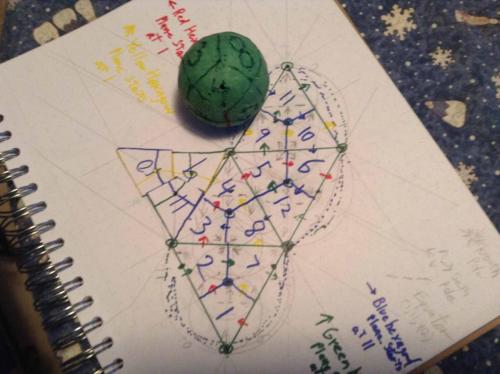
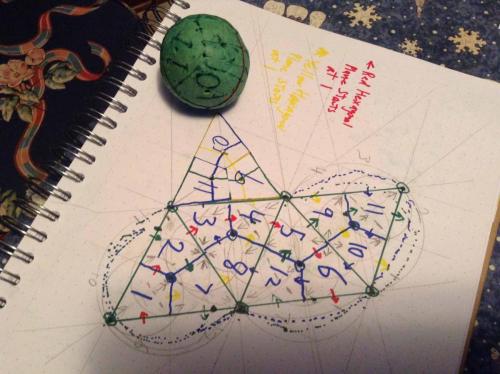
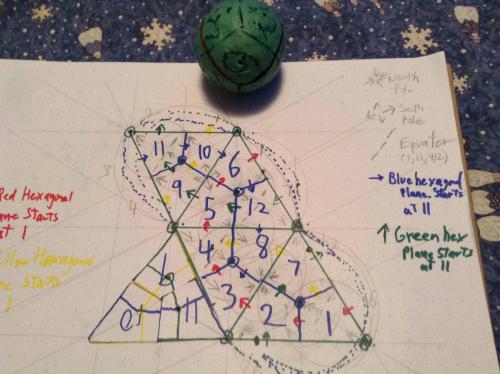
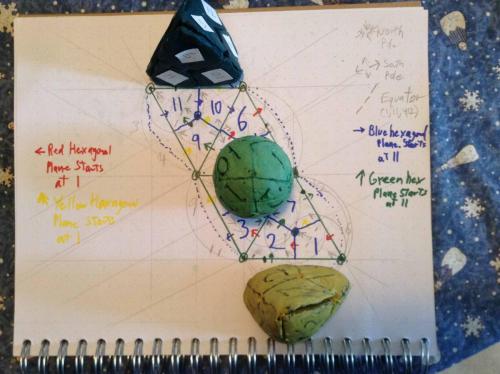
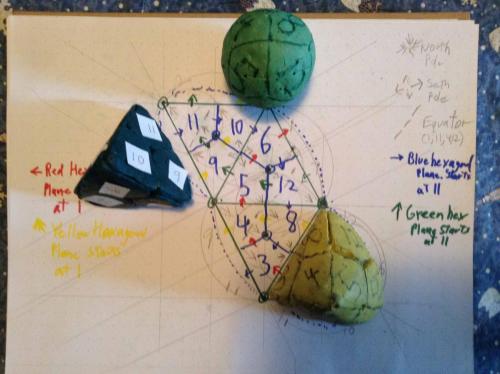
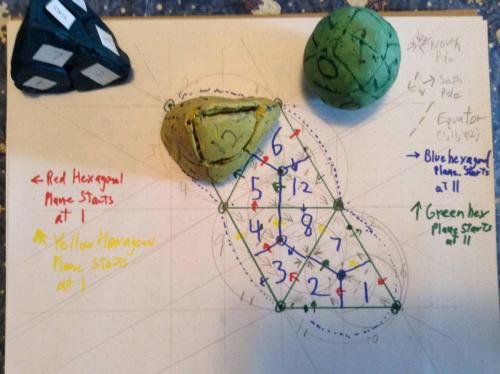
Thread, Beautiful layout of the open shields came to me this morning (actually yesterday, or Friday morning). (open shields are made only of lines one diameter or one radius long, excluding the two short lines indicating the "open" part of the shield.) Presented here looking at the sphere from the outside. The old picture of the triangle is perfectly valid, as a stamp image, or as looking at the sphere from the center of the sphere, outward. Studying the new layout of the spheres gave me two insights. One, what looks wrong at first, is not, and two, my confusion with the green and blue hexagonal planes comes from the fact that the green is not continuous in the presentation, and is divided up into three thirds of a great circle. This combined with the fact that I switched 11 and 12 conceptually, in terms of how the direction of increasing degrees on the plane leaves the diamond. In the case of 11 blue goes up and to the right (conceptually going with the first layout I presented with the four equatorial diamonds, the four diamonds touching the North Pole, and the four touching the South,) whereas in the case of 12 the blue goes down and to the right and the green goes down and to the left.) This is because 11 and 12 are directly opposed and the blue and green planes cross at both 11 and 12. Interesting to note that 11 and 12 are therefore the only two diamonds that are not included on either the red or yellow hexagonal plane. In my original convention I tried to take this potential confusion into consideration by having each color plane have three diamonds with a capital letter, indicating "heading North" and three with a little letter indicating "heading South" and then added another convention where the order of the two colors addressed in a diamond would be the one whose arrow was running SW to NE or NE to SW and the second letter would be that of the color running SE to NW or NW to SE. While I am sticking to these conventions, it is easy to get fouled up with your directions because once you leave the vantage point of looking at diamond 1 with diamond 2 up and to your right, the ideas of up and down and left and right, change as you proceed the 360 degrees around the plane. Again, enough words. Study these pictures of looking at the sphere from the inside and the outside, and after a few minutes, what looked wrong at first, will make perfect sense, once you get inside/outside, up/down, left/right, clockwise/counterclockwise, North/South, and East/West all put in their proper places. Regards, TAR
-
Dividing a sphere into twelve "identical" shapes.
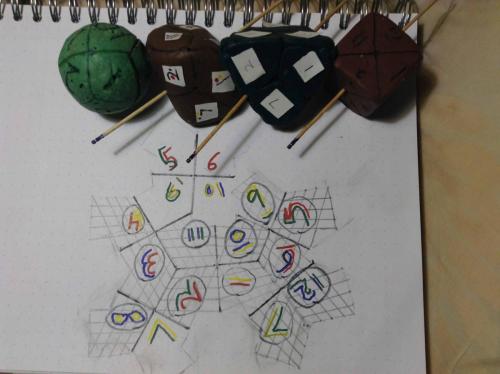
Thread, Here I have taken a toothpick cut to the length of one diameter of my 1/4lb sphere (118 sixtieth of an inch, almost 2inches) and made a cross on the paper, which is identical to such a straight line on the sphere, except for, on the sphere, the line is curved as a segment of a great circle around the center of the sphere. I then proceeded to make six such crosses, which is exactly how many of such crosses there are on the sphere. On the sphere the ends of the crosses touch exactly, as exhibit by the Spherical Rhomic Dodecahedron. They do not touch exactly on a 2d surface, because the 90 degree angles and the 120 degree angles work out differently on a sphere than they do on paper. But here is a nice application of the 12 segments of the sphere, and the numbering system I have stuck to in this thread. The 15 degree grids of the diamonds of the SRD have been drawn on the 2d surface, making sort of an open diamond shape. The twelve sections of the sphere, numbered 1 to 12 are circled in black (as there are some duplicate numbers so you can imaginarily wrap the crosses around to touch the proper end of the next cross in the proper orientation.) The grids are drawn from one side of the diamond on the SRD to the other, and with this you can visualize the distortion, and thus the correction when seeing the grid on the diamond, the shield shape on the equilateral triangle, and the "open" shield shape here. Regards, TAR note the alternation between three points and four points is exactly the same as on the SRD. Every four point has four radius long line each extending to a three point. Every three point, has three radius long lines, each extending to a four point.
-
Dividing a sphere into twelve "identical" shapes.
Or I can just keep posting the ground I am covering and people can take it for what it is, old or new.
-
Dividing a sphere into twelve "identical" shapes.
Thread, I was searching around the web today to see what, if anything is "new" about this thread. Every component of the thread is pretty much already noticed in one way or another, and in that there is nothing new here. After all a shape is a shape and its geometry is not dictated by imagination. The four hexagonal planes have already been noticed. The Spherical Rhombic Dodecahedron has been know for a long time. Same with the cubic octahedron, the close packed spheres and everything else mentioned in the thread. Projections of the Earth onto tetrahedra and equilateral triangles has already been done. In that this thread is just having fun discovering all those things for myself, (ourselvers). Where I have not found anything exactly alike is in three areas. My late December insight of labeling every point on the sphere in accordance to the 360 degrees of each of the 4 hexgonal plane circles. The Sedge. Finding that dividing up the diamonds into grids can be exactly matched on an equilateral triangle. Other projections of the globe onto a tetrahedron I found were similar, but did not exactly match and use the same scheme. I think they are all fine, but the difference I see with this scheme is that its a projection of the sphere onto a 2d rendition of a sphere, not the projection of the sphere, onto a flat surface. What I mean is that this scheme has a grid that can be transferred exactly from the 2d version to the surface of the sphere, or from the surface of the sphere to the 2d triangle. It's like projecting the surface arrangement of the sphere, with a light at the center of the sphere onto a larger sphere. All the symmetries and relationships are maintained. All the points on the tetrahedron could be named with exactly the same 360 degree four hexagonal plane scheme I presented in December. This I just demostrated by drawing my grids of the SRD's diamonds, onto the equilateral triangle. I could not find any images on the web of the equilateral triangle divided up into the shields exactly like that. It surprises me that I do not find it, because it is so simple and beautiful, I would have expected to find it. My conclusion, is that I may have, over the last month or so, actually made a contribution to humanity. Which is something I have wanted to do for 5 years now, starting one day when I suddenly realized I was 56 years old and if I was going to make a contribution to humanity, I better start soon. I had begun with CDs and books trying to learn Arabic, Russian, Brazilian Portuguese, Chinese, Japanese, and Hindi, on an investigation to find the meaning behind language. I have, as you can tell, sort of switched my focus, playing with clay balls, and these twelve sections of the sphere (cube, octahedron,tetrahedron) and thinking about the ways this scheme helps understand the way the geometry of the world is, as well as the way we internalize the world and build an analog model of it, in the synapes and structures of our brains. This particular post is a question to anyone reading this. Are you finding this particular investigation as fun and interesting and rewarding as I am? Am I doing something here? Or am I just going over old ground? Regards, TAR
-
Dividing a sphere into twelve "identical" shapes.
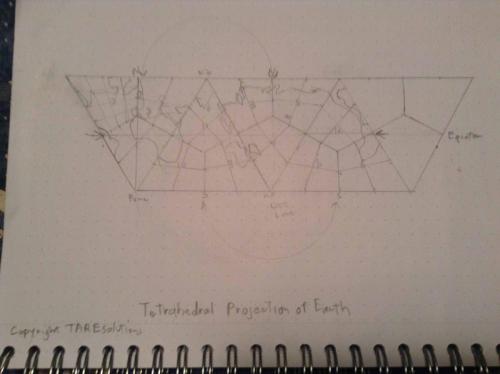
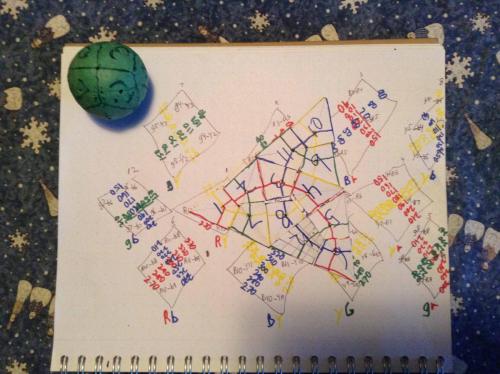
Spherical Rhombic Dodecahedron divisions made of Earth and transferred to the exactly related shields of the twelve divisions of the tetrahedron, and placed on the Sedge pattern in accordance to the scheme being discussed. Angles and distances maintained with minimal distortion.
-
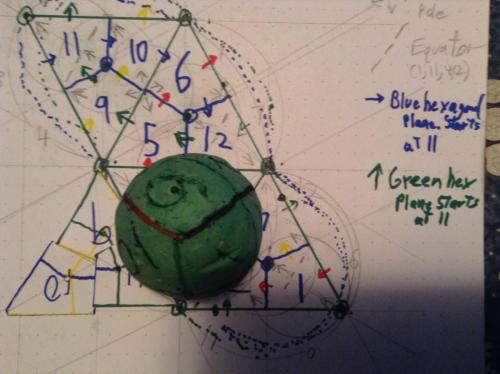
Dividing a sphere into twelve "identical" shapes.
Thread, I am really liking this scheme. Built out into a really interesting hexagonal plane with several sorts of hexogonal symetries. Allowed me to verify that my green and blue are correct (still did something wrong, but have not isolated it yet.) And allowed me to pick a way to orient it nicely to the globe, with North up and South down, and the equator through the middle. Flipped the page over to get the right "outside" orientations, to match my 10 degree divided ping pong ball, with 1 showing the red plane up and to the right, and the yellow up and to the left. And 11 showing blue going up and to the right and green going up and to the left. (0-360 in each case.) Will make a nicer one later, have to go to bed, but wanted to show this because it allows for the projection of the sphere onto 2D with litle distortion, and keeping distances and angles fairly true. Same scheme allows projecting the surface of a sphere onto a cube or tetrahedron or octahedron (or Sedge), and even to give a name to every direction in the galaxy (from here, or from the center). Just a darn nice scheme, that looks nicer and nicer the more I play with it. Thread, Woke up and was looking back in the thread a few posts at the 8 sided figure I made in response to Commander's challenge. It reminded me of an arrangement I made two nights ago (but did not post), trying to figure out why you can draw a triangle on a sphere, but not larger than the equator, but the whole sphere is in the shape of an equilateral triangle. I had started with the three lines each a diameter long (may be a third of the circumference, I am not sure yet) and thought if this was a triangle then a six sided figure made on the surface of a sphere with the same three lines drawn on it, made by drawing a great circle line on each side of each of the original lines, of the same length, would be a slightly smaller triangle. I kept making a smaller and six side figure (Like your thumb and first two finger with thick gloves on, your thumb and first to fingers without gloves on, just the bones, and then three toothpicks touching at one end and making a triangle with the other,) 'til I wound up with the exact three tooth picks coming from the other end of the sphere. If you are have trouble visualizing, take the thumb and first two fingers of your right hand an make a little one inch equilateral triangle with the tips of your fingers. Do the same with your left hand. Then put the thumb of your right hand in the triangle you made on you left and keep going until your right thumb hits the crouch between your left thumb and your left pointer. Anyway, made me realize that the 2d equilateral triangle has yet another purpose. If its marked out with the twelve sections of the sphere, and you want to do something mentally with the sphere, do the thing with the triangle, which is the surface of the sphere, and then mark the thing you did on the surface of a sphere laid out with a numbered spherical rhombic dodecahedron pattern. It will be exactly right, down to the precision with which you marked the surface of the sphere and the equilateral triangle. Regards, TAR or vice a versa
-
Dividing a sphere into twelve "identical" shapes.
Thread, OK, here is the finished product. Same scheme, with the 360 degrees on the four hexagonal planes, but instead of the 12 disconnected diamonds showing the scheme in 2d we have now 12 connected shields, so there there is no question how the one point relates to another. The triangle actually folds in four pieces and if you make the three points touch, you have your tetrahedron (or sphere). Its upside down and backward, being a stamp of the spherical rhombic dodecahedron inspired Sedge, but I am wondering if it works if you connect the points by pulling them up, so that you are looking at the inside of the sphere. Not sure but that might be good. Notice, because of the dual nature of the figure we have been working with, that you can see the 6 squares and 8 triangles of the cubic octahedron. I give you TAR Spherical Coordinates. Regards, TAR Thread, The 2d triangle layout is what you would see on the inside of the sphere, should the outside be layed out like a spherical rhombic dodecahedron with the diamonds. (more or less) The pattern is the same. I took my clay and cut it in quarters and made 1/4-3/8 inch thic equilateral triangles and drew the shields and hexagonal planes on it, as in the last post. Then I squeezed the bases of the triangles to lengthen the short lines and then rounded the point a bit to shorten that line, so the shields where diamonds and the quarters were in the shape depicted earlier, two making a Pacman. Then I put the Pacmen together and formed it into a sphere, (after putting the inside lines of each piece on the outside exactly where they were). Then I cut open the sphere into the triangle. Regards, TAR Ok, not a finished product. I screwed up and crossed the green and blue planes somewhere along the line. I absolutely did not want to do that, since I was setting the conventions, they had to stay correct. So, as pretty as it is, I have to withdraw it, because its wrong...or it's right, and the 12 pictures I took of each of the twelve diamonds laid out in 10 degree grids, is wrong... Let's do this. Call it a draft, with the basic idea, but with blue and green crossed up.
-
Dividing a sphere into twelve "identical" shapes.
Thread, Summary of thread so far, in a picture. 1. Six pennies around a central penny forming a hexagon. (not shown) 2. 12 balls dense packed around a central ball forming 4 hexagonal planes and 3 square planes. (cubic octahedron)(Pink) 3. Position of twelve balls placed on the surface of a sphere. (Spherical Rhombic Dodecahedron, light green) 4. Same twelve sections oriented to a cube. (Brown cube)Leading to the grid divisions and then the numbering of the divisions according to the 360 degrees of each of the hexagonal planes. (not shown) 5. The twelve sections placed on an octahedron (not shown) and then a tetrahedron. (Dark green) 6. The tetrahedron rounded into a Sedge (brown one faced, one edged, two verticed item on bottom right.) 7. Stamp image of the Sedge laid out in two dimensions. (central image) 8. Top equalateral triangle rotated down to lower left to form one large equilateral triangle, which can be drawn on a sphere with three straight lines along three great circles eminating from one point (possibly one diameter long each). (light green) Regards, TAR (all clay figures same volume made with 1/4lb of clay, exception is 13 ball arrangement, 12 balls made from 1/4lb of clay, one central dark pink ball presumeably 1/48lb from different stick)
-
Dividing a sphere into twelve "identical" shapes.
Thread, I took a purple, orange and lime green marker to follow the lines around my equilateral triangle, on the surface of the green sphere I made, marked out with the spherical rhombic dodecahedron diamonds. Was expecting the lines to meet in some funny zig zag way, like following the lines around the tetrahedron. Little did I know, that I did not have to make any twists or turns at the three points. Simply drew three straight lines through three of the four points on the sphere. Turns out, the point of the 1,6 and 10 diamonds(shields) is the same point and the three lines that define the equilateral triangle are a line from this point to the tip of the 8 a line to the tip of the 3, and a line to the tip of the 4. Enough words. Take a look. Its so simple and beautiful I don't know why I was not taught this in school.
-
Dividing a sphere into twelve "identical" shapes.
OK thread, This is getting really neat. I redrew the 2D Sedge layout and cut it out, and it of course made a tetrahedron when you fold it on the three internal lines. (Upside down and backward from the layout on a sphere, but otherwise perfectly related.) But then I cut out the shield shapes and found I could rearrange them, taking one whose outside edge touched the outside edge of a distant shield in the same association as found on the numbered diamond sphere, and I continued to do it, and it made this nice equilateral triangle. Who knew that the surface of the sphere was in the shape of a triangle! Measured my pieced together triangle a few times and averaged out the base to 320 and the height to 279. This multiplied out to 44640. using 118 as the diameter and figuring the surface area of the sphere, I got 43743. These are .98 and 1.02 of each other. Pretty close. As if perhaps pi might be found within the proportions of an equilateral triangle. And within the proportions of a spherical rhombic dodecahedron's diamond.
-
Dividing a sphere into twelve "identical" shapes.
But back to the Spherical Rhombic Dodecahedron and how to transfer it to a 2d surface. Create the 12 sections of the tetrahedron and each SRD section correlates exactly to one section of the tetrahedron. Using the Sedge (three tetrahedron edges rounded) the transfer of the tetrahedron faces to a 2d (four triangle) shape becomes evident. Of course everything is backward and upside down, and the choice of where to start (which diamond in what orientation in what position is to correspond with what position on the sphere) is arbitrary. But once you start, every other position transform from the sphere to the 2d surface is exactly determined. (provided the grid system is drawn on both the sphere and the 2d surface, on the diamonds (and shields) shown. Sphere Area= 4pi r squared = 4 pi 59 squared = 43,744 (using crude measuring with the 1/60th of an inch unit, and an approximately 1 inch diameter sphere) (actual square degrees in a sphere 41,250. Triangle Area = 1/2 base times height. The triangles shown measured all over the map, so better precision is definitely possible, but going by a base of 145 and a height of 140, with 4 of them, it comes to 40,600. Close enough to imagine a 1 to one correspondence between a division of a diamond on the sphere and a division of a shield on the 2d diagram. The boundry lines between the diamonds on the sphere are all 1r. The boundry lines on the tetrahedrons are different, with a different length touching three points than touching 4 points, but it looks regular and forgiving. Would be interesting to see what a globe would look like projected onto this. Or twelve photos taken in twelve directions and pasted on the tetrahedron or the 2d scheme...lots of thoughts.
-
Dividing a sphere into twelve "identical" shapes.
Attempt one not shown. Attempt 2 and three shown twice, repositioning the figures between shots. These are divisions into 8 sections and not directly related to the thread (perhaps, but I have not seen the connection.) Its (the eight) is two square planes on top of each other, rotated 45 degrees from each other. Have not "seen" if that builds out to the same matrix behind the spherical rhombic dodecahedron. (talking about attempt 3 with the eight large diamonds, four touching at the North and four at the south) I think the eight start a different matrix. the square planes in the 12 have each ball touching 4 balls in the next plane, where here it looks like two here. Sorry, those are lousy and confusing pictures. Each of the two balls is showing something different. The one with the toothpicks is the eight diamonds with a pick at the North pole, the south, four equal distance from each other in the Northern Hemisphere, and four in the South. They form the vertices of the diamonds. Two four points at the poles and eight three points, four each equal distance from the respective poles and spun around the axis of the poles 45 degrees from each other. The other ball is eight tangerine slices, but four form a hemisphere as do the other four, but the one hemisphere is spun 90 degrees to illustrate how the great circles are imaginarily cut in quarters, so that one can say the unseen vertex is there, cutting the one semi great circle into two "sides" of the diamond (the 180 degree angles of the elongated diamonds with the 45 degree angles being at opposite podal points.) Confusing the picture even more is the fact that of the eight tangerine sections I drew a grid in two of them to indicate the opposite nature of the "sides" of the diamonds.
-
Dividing a sphere into twelve "identical" shapes.
Actually my figure worked except the sides might not have been on great circles. When I forced them onto great circles I got a tangerine section set up so the "diamonds" had four points, two with internal angles of 45 degrees and 2 at 180 degrees (two sides on a great circle and the other two sides on another great circle. So you might disallow both those attempts, but then on a third I found you could simply make four diamonds touching at the North Pole and 4 touching at the South pole, the bottom tip of the North ones being way in the southern hemisphere and vice a versa.
-
Dividing a sphere into twelve "identical" shapes.
Commander, "Strangely, there is no way of producing 8 equal Square faces on the Sphere, Using 2 tetrahedrons in a mirror tilt may produce 8 equidistant points on the surface of the Sphere but connecting them may again result in Triangular shapes and not squares." I took this as a challenge and was thinking this morning about it. I think I succeeded in making such an "Impossible" division of the sphere into 8 four sided figures, with all four sides being the same length, and on the surface of the sphere, and I believe each line is on a great circle. I will make it again and take pictures of it, tonight. TAR
-
Dividing a sphere into twelve "identical" shapes.
Commander, Post 70 in this thread shows my version of your roofed cube. The divisions are the same in terms of internal angles (90 at the 4 points and 120 at the three points.) Except to retain the 12 divisions you ignore the edges of the cube, and count half a diamond as your 1/4 roof on one side, and combine that with its neighboring 1/4 roof on the touching side. I will have to accept your statement that you can not make 8 equal diamonds. Seems the 12 sections work out so nicely to divide the tetrahedron, the octahedron, the cube and the sphere, it would be unlikely to suspect that another number, other than 12 would work as well. I had not been able to see the relationship of the cube octahedron I started with, to the dodecahedron with the pentagonal sides. Perhaps now that using 10 out of the twelve tetraheral sections to make that five sided figure a few posts ago, there might be a relationship, after all. However, the spherical rhombic dodecahedron, is still the better of two dodecahedrons, as far as I am concerned. It has the cube, octahedron and tetrahedron built in. It has the 4 intersecting hexagonal planes. It has the 3 intersecting square planes. The diamonds can be divided in a grid pattern, seemingly proportionally around the hexagonal planes, into degrees, minutes, seconds and fractions of seconds, which you can not do with the pentagonal dodecahedron. If you imagine a ball at the center of the figure, 12 balls of the same diameter will fit exactly around the center one, if placed exactly in the middle of each of the 12 diamonds. This pattern of hexagonal and square planes, that is thusly indicated, can be extended outward indefinitely. Each of the sides of the diamonds appears to be exactly one radius of the sphere that the spherical rhombic dodecahedron is drawn onto. Any one of the said 12 sections of the sphere can replace any one of the 12 sections of the cube, the octahedron and the tetrahedron, in terms of the sections' internal angles. Because of this, mapping the surface of any of the shapes to the other could be done, in terms of the designations of position on the sphere according to the hexagonal plane 360 degree grid model shown earlier. Regards, TAR
-
Dividing a sphere into twelve "identical" shapes.
somehow the sections wind up with that 36 degree angle. Two make 72 degrees, 5 make 180 and 10 make 360.
-
Dividing a sphere into twelve "identical" shapes.
Thread, Cut up a 1/4 pound clay tetrahedron into the 12 sections and replaced one Sedge section with one Tetrahedron section and vise-a-versa. Show the twelve sections. Then the surprise. I put the sections outside face to outside face to see how they would pack, and got six peices that unexpectedly fit together as shown. 10 of the pieces completed a circular pattern with a flat side. The other two pieces made the 6th piece which fit nicely upside down in any one of the five "places" for it. Seems the sections will pack nicely. Regards, TAR
-
Dividing a sphere into twelve "identical" shapes.
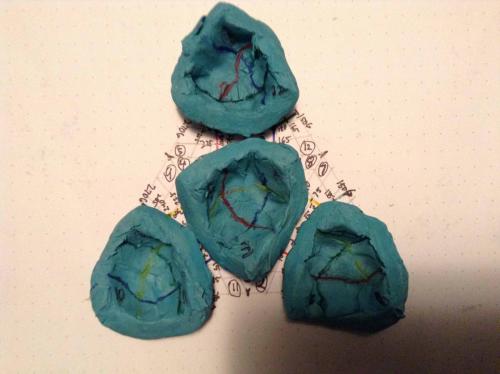
Thread, Was cutting a Sedge into its 12 sections. Just got the first section cut out and realized they were not going to all be identical. Then I thought that was because some edges of a Sedge section were cut from the edge and some from the face. Then I realized I could not have that issue if I never rounded the three edges required to make the Sedge in the first place... Don't remember if I ever made the 12 sections of the tetrahedron. If not, I will soon and post them. Seems those twelve sections should be very interesting with interesting properties. Might even be a way to pack space with them. Just a waking thought. Will pursue it later. Regards, TAR
-
Dividing a sphere into twelve "identical" shapes.
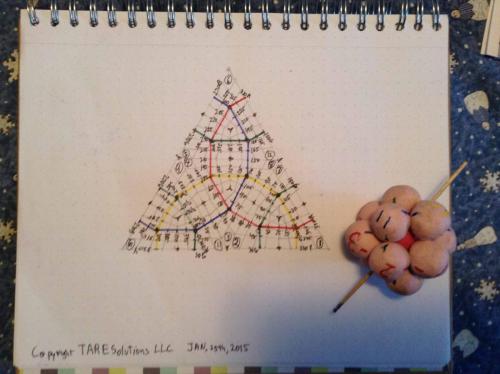
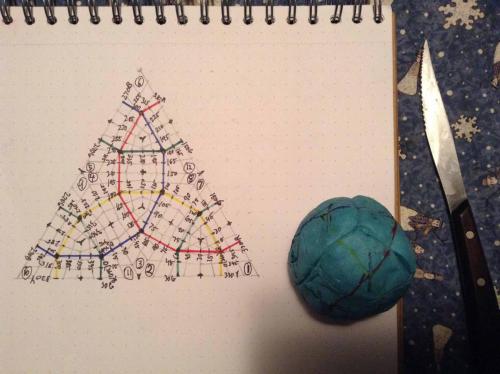
Thread, While cutting the diamonds off the surface of a sphere I accidently came up with a 1 faced, 1 edged, 2 verticed figure that I started a thread on, and continued to investigate. I can make it at will now (based on a tetrahedron,) and it has a definite relationship to the twelve sections of the sphere. There are left handed and right handed versions of the thing, and you can "start" the thing on any of the twelve sections, in each of the four orientations possible. The numbering scheme I suggested earlier can be readily applied to this figure, and the imprint of this figure on a 2D surface. The Red hexagonal plane describes a nice semicircular arc (open to the NW) (1,6,5,4,3,2) The Blue hexagonal plane describes a nice semicircular arc (open to the SE) (11,3,8,12,6,10) The Yellow hexagonal plane describes an S to the left and down (1,7,8,4,9,10) And the Green hexagonal plane describes a S tilted to the right and up (11,9,5,12,7,2) Regards, TAR (copyright TAResolutions LLC) (sorry my NW and SE, up and to the right is all 90 degrees off, I took the picture after rotating the book 90 degrees CW)
-
Dividing a sphere into twelve "identical" shapes.
Imatfaal, I thought it interesting today to think of the various shapes and trials and thinking that led me to the pingpong ball close packing and the cubic octohedron, and the figure I learned through this thread was the Spherical Rhombic Dodecahedron, and the Janus and the 12 sections of the sphere, and the cube and the octahedron, and finally the tetrahedron sphere and the six pennies around a central penny that I started with. Interesting, because I realized I had made the tetrahedron sphere when I was 10 years old, taking the the ball of gum out of my mouth and pressing it between the thumb and forefinger of both hands. And here your picture is of the interlocking tetrahedron. Long way to go, to get to the figure so easily and naturally formed by a 10 year old. Regards, TAR
-
Dividing a sphere into twelve "identical" shapes.
Thread, Here are two unillustrated methods to make the pattern (spherical rhombic dodecahedron) on the surface of a sphere. 1. Place a mark anywhere on a sphere, call it your North Pole. 2. Flip it 180 so that your mark is directly down and place another mark at what is now the very top, and call this mark your South. 3.Hold your poles level to the ground, for bearings and place a third mark directly between. 4. Place a 4th mark opposite your third. 5.Place a 5th mark directly centered between your current 4 and a 6th mark directly opposite this, so you wind up with a Norh Pole mark, a South Pole mark, and 4 equally spaced marks around the equator. 6. Now you need eight more marks to fully describe the vertices of the diamonds. You have just placed the 6 four-point vertices and need to now place the 8, 3 point vertices. 7. Take the sphere and put North directly up, you will see the North Pole and any two of the equatorial marks make a triangle. Place a mark in the center of this triangle, equal distance from the North Pole, the one equatorial point and the other. 8. Repeat this procedure three more times related to the North Pole and the equatorial points as you turn the Sphere 90 degrees each time. 9. Flip so the South pole is up, and place your next four in the same manner as in steps 7 and 8. 10. Now draw four lines down from the North pole, one to each of the marks you made in steps 7 and 8. 11. Flip and draw four lines down from the South pole to the marks you made in step 9. 12. Pick an equatorial mark, which is a four point and visualize an x on this mark extending to the two nearest ends of the lines coming down from the North, and the two nearest ends of the lines coming up from the south. Draw this x. 13 Turn 90 degrees along the equator to the next mark and draw the x again. 14. Turn 90 degress along the equator and draw the x again. 15. Turn 90 degress and draw the x again. Second procedure. 1. Create an object, (like a string or toothpick) that is one diameter of your sphere, long, with a reference mark at its middle. 2. Make an X on your sphere, marking the length of your object and the middle and then an other line crossing the first at 90 degrees. Calll this your North 4 point, with attending lines. 3. Make a South Pole X in the same manner, so that the lines are headed for, but of course will not reach, the North Pole lines (Visualize two great circles bisecting each other) 4. You will find your diameter marking object exactly reaches between the tip of a line extending from the North Pole, and the next line 90 degrees over, coming up from the South. Draw this line, and make an X out of it, by placing your marker at its center turned 90 degrees. (You will see this conviently, also lines up with the ends of a line coming down from the North and one up from the South.) 5. Make the other three Xs around the equator. In both cases you should wind up with the 12 diamonds describing the Spherical Rhombic Dodecahedron. There are other ways of course to get to the figure, as we have described, finding the center points of the diamonds with the vertices of the cubic octahedron and so forth, but these two methods are the quickest and easiest I have found so far. Regards, TAR
-
Dividing a sphere into twelve "identical" shapes.
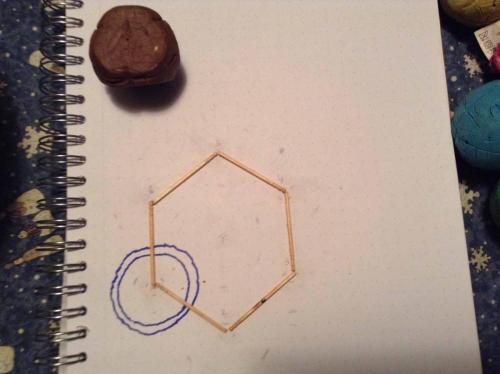
Taking the tetrahedral figure, with the edges being exactly two r long, and rolling it along the edges, you can describe a perfect hexagon on a 2D surface. Notice that 6 balls, placed exactly on the vertices of this hexagon, will fit exactly, as securely as 6 pennies around a central penny. The 118D toothpick lengths were placed on this track to prove that the toothpick lengths are 2r or one D, each. The spherical rhombic dodecahedron can be completely described on a sphere with 6 orthogonal crosses made with toothpicks of this diameter length. Quite interesting that three Janus sections, make a 1/4 of a sphere, and each edge of one of these quarter sphere shapes, along the surface of the sphere, is exactly on diameter in length.