jalaldn

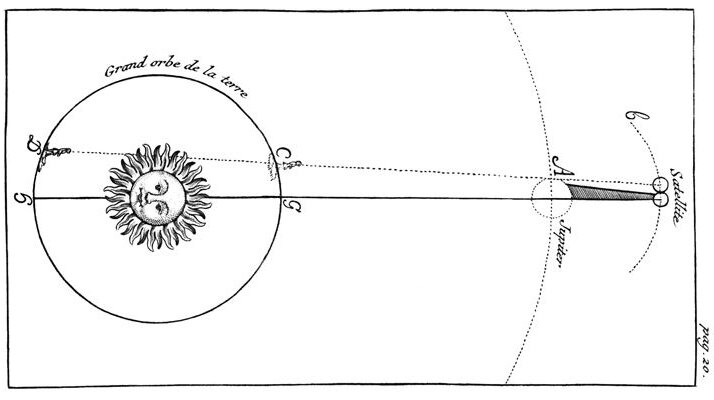
Even if we accept that errors are natural to humans, why, after so many years, have they still not corrected them? Error one According to Rømer, light took approximately 22 minutes to cross the diameter of Earth’s orbit. Error two Earth–Sun distance (1 AU) light takes to travel → 11 minutes What did Rømer actually measure: the Sun or Jupiter's moon Io? Error three Can't they even write properly whether it is 5:35:45 pm or 5:35:45 am? The single most important observation (the one Rømer quoted most): November 9, 1676: The moment Io began to disappear behind Jupiter Actually observed time → 5:35:45 PM (Paris local time) Expected time according to existing tables → 5:25:15 PM Difference = +10 minutes 30 seconds (delayed) In August 1676, when Earth was closest to Jupiter, Io's eclipses happened on time (or slightly early). But on the same year, November 9, 1676, when Earth was farthest from Jupiter: Expected time for Io to emerge from shadow: around 5:25 PM Actually observed emergence time: 5:35:45 PM (Paris time) → Delay = about 10 minutes 45 seconds If they wanted to confirm whether Io would appear at 5:25 or 5:35, they had to start observing Io at least 3.5 hours earlier, because the countdown starts only from the moment Io disappears; only then can the re-emergence time be measured. Looking at this, they could not have started at 2:30 in the afternoon. Because even today it is difficult to see Jupiter at 2:30 pm in daylight; with the technology of that time, it would have been impossible to observe Jupiter's Io at 2:30 pm during the day. From this it becomes clear that when they say 5:25 or 5:35, it cannot be evening; it must actually be early morning. That day's sunrise was at 6:29 am. Moreover, Ole Rømer decided to measure the time light takes to cross the diameter of Earth's orbit. Looking at this, he would have tried his observations only when Jupiter was as close as possible to the Sun (i.e., in opposition or near it), because only at those times does the light from Io cover the full diameter of Earth's orbit to reach us. Only then could he say “what I measured is the time across the full diameter of Earth's orbit.” Look at this picture. In this image, it may appear that GS (the Sun) looks smaller than CD (Earth), but in reality, that's not the case. Why? Because you can line up 215 Suns across the diameter of Earth's orbit. Therefore, the thickness/blocking by the Sun wouldn't be enough to reduce the size of Earth's diameter (in the way it might seem in the image). discussion link https://www.researchgate.net/post/Ole_Romers_discovery_is_a_historically_significant_discovery_Why_are_there_so_many_errors_in_recording_uploading_the_data_of_this_discovery

Even if I don't fully understand what you're trying to say here, I'm responding with the thought that this answer might be correct. If you believe that when a light source is 11 minutes away (in light-travel time), it takes 11 minutes to notice when the light is turned off, and similarly it takes 11 minutes to notice when the light is turned on, then Ole Rømer could never have discovered that roughly 11-minute discrepancy. The very fact that Ole Rømer was able to discover it means: Even though light takes time to travel, everything we see is happening in real time — no matter how far away it is.

If you believe that it takes 11 minutes to sense when light is blocked from an object that is at a distance light travels in 11 minutes, and similarly, it takes 11 minutes to sense when light is emitted, then you will never be able to make this calculation.

If the Sun's diameter were reduced to just 1 centimeter, here's what Earth's orbit would look like in the same scaled model: - Actual Sun diameter: ≈ 1,391,000 km - Actual average distance from Earth to Sun (1 AU): ≈ 149.6 million km Scale factor: Real Sun diameter ÷ Model Sun diameter = 1,391,000 km ÷ 0.00001 km = 139.1 billion times smaller Applying the same scale to Earth’s orbit: Model distance from the Sun to Earth = 149,600,000 km ÷ 139,100,000,000 ≈ 1.075 meters So, in this model: - The Sun is a sphere only 1 cm in diameter (about the size of a small marble or a peanut M&M). - Earth orbits at an average distance of roughly 1.08 meters from the Sun’s center. - The full diameter of Earth’s orbit (from one side of the orbit to the opposite side, passing through the Sun) would be about 2.15–2.16 meters. In everyday terms: If you placed a 1-cm Sun in the middle of a small room, Earth would be circling it at about arm’s length — roughly 1 meter away! If the Sun were one centimeter in diameter, the Earth would be one meter away, while Jupiter would be 5 meters away on the other side of the Sun. (Looking at this, even if the Sun is between Earth and Jupiter, it won't cause any major obstacles.)

Eclipses visible on the eastern horizon just before sunrise will be on the opposite side of the Sun. Similarly, eclipses visible on the western horizon after sunset will be on the opposite side of the Sun. How did he discover the speed of light? Okay, in the calculation you're going to give, you can add or subtract 10 percent. Give me that amount, I need to get 11 minutes out of it.

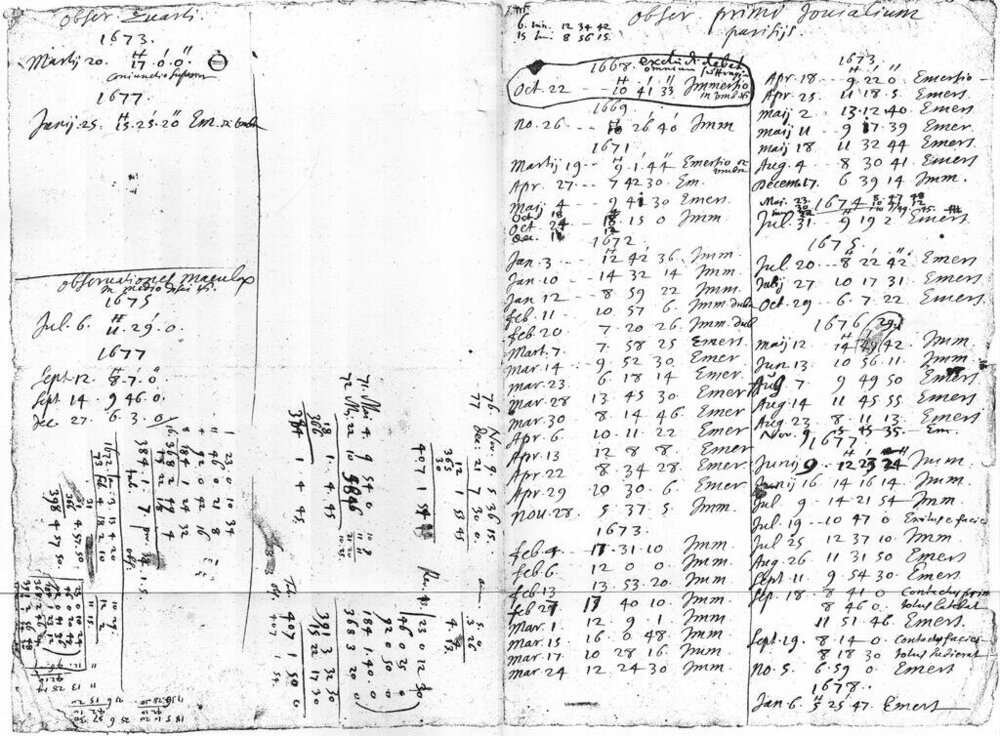
The text in the image appears to be handwritten meteorological or observational data from 1673, possibly recording conditions such as temperature, precipitation, or other measurements. The phrase "11 minutes io not visible" refers to a specific observation, indicating that on a particular date (possibly April 18, 1673, as mentioned in the data), an event or object labeled "io" was not visible for 11 minutes. Here, "io" could be a typo, abbreviation, or misinterpretation. It might refer to an astronomical event (e.g., Jupiter’s moon Io, observed by astronomers at the Paris Observatory during that period) or a concealed instrument reading or condition. Without additional context or a clear definition in the document, "io" cannot be precisely identified. The surrounding data includes dates, times, and measurements (e.g., "9:22:0 Emero"), which may relate to time intervals or meteorological events. With my current tools, I cannot search the internet or further analyze the document, so this is the best understanding based on the provided content. If you’d like to learn more context, I can assist with a search—would you like me to do that? https://commons.wikimedia.org/wiki/File:Ole_R%C3%B8mer_-_Obser._Primi_Jovialium_Parisiis_-_pp1%2B4.jpg (The people who came after Ole Rømer didn't write the data properly, they didn't even consider what he could have seen. Ole Rømer saw an 11-minute variation. Consider what he could have seen. Even in the data here, they mention the radius of the Earth's orbit instead of the diameter.) The top of page 4 lists observations of the fourth moon of Jupiter (Callisto). At the lower half are a couple of attempts to match the number of revolutions ("Rev.") of Io with an average orbiting time for three periods, 76-77, 71-72 and 72-73. Next to them are what according to Meyer p. 19 appears to calculations of an average value of the time it takes light to travel a distance equal to the Earth orbit radius (ca. 11 minutes). At the bottom, written upside down, are calculations of eclipses in Paris based on observed eclipses at Uranienborg.https://commons.wikimedia.org/wiki/File:Ole_R%C3%B8mer_-_Obser._Primi_Jovialium_Parisiis_-_pp1%2B4.jpg

Ole Rømer did not mention the number 22 anywhere, he only mentioned 11. The confusion arose because later people wrote Astronomical AU (Astronomical Unit) instead of the diameter in the orbit of the Earth. He calculated that it takes light 11 minutes to cross the diameter of Earth's orbit around the Sun. If we calculate at that point with this speed, the speed of light would be 460,606,060 m/s. In that case, the already accepted speed of light, which is 299,792,458 m/s, would become wrong. But I am not saying that it is wrong. What I am saying is: in the very first second from the beginning, the speed of light was 299,792,458 m/s, and then it gradually increased (with acceleration) and rose to a speed of 460,606,060 m/s. In that case, before light even enters the diameter of Earth's orbit, it has already traveled a distance of about ~4.2 AU . At that time, it would have roughly taken around 20 minutes just for that distance. On that basis, I mentioned that (because of the acceleration) the speed is higher than the currently accepted speed of light. Tell me in full how he found those eleven minutes by calculation, and only then will you understand its depth. No history is needed, just calculation is enough I agree that no measurements were precise in his time, but I cannot accept that time was not precise. (Even then, there were only 24 hours in a day.) Now that we have measurements, we discuss them based on them. When we think that the distance from Earth determines Jupiter's Io orbital period, we are making a mistake in our math. Jupiter's Io orbital period cannot be changed by its distance from Earth.

Did Ole Rømer measure the speed of light by looking at the Sun or at Jupiter's Io? If he measured it by looking at the Sun, it would be the radius. Or if he measured it by looking at Jupiter's Io, it would be the diameter.

The speed of light is not a constant value. Its speed involves acceleration Ole Rømer conducted a study. Based on the time he studied, there is a possibility that the Earth's orbital path and distances could be incorrect. In fact, they were incorrect. However, the times he specified were not wrong, and there is no necessity or possibility for them to be wrong. When the Earth's orbit diameter is larger, it is 3.04 × 10¹¹ m ; when it is smaller, it is 2.94 × 10¹¹ m The time taken for light to cross the Earth's orbital diameter when it is larger is 16.898 minutes, and when it is smaller, it is 16.342 minutes. Based on the current speed of light, it takes 16 minutes to cross the Earth's orbital diameter. Ole Rømer specified 11 minutes. However, light covered that distance in just 11 minutes, meaning the speed of light at this point is 1.45 times faster. Although it is traveling at a rate of 1.45, considering the distance from Jupiter to Earth, only one-third of the total journey comes to our attention. 9.68 × 10⁸ km ÷ 3.04 × 10⁸ km ≈ 3.184 That is, due to the presence of acceleration before entering Earth's orbit, it would have entered at a speed greater than the speed of light. Therefore, it can only be called acceleration, but for now, I am not in a position to specify what its ratio is. ( Maybe even if I set it to 25% for at least a quarter of an hour, its speed will double in hour. ) Let's look at it from another angle to prove that the measurements we are currently using are wrong. "What is the true speed of light: 299,792,458 m/s or 460,606,060 m/s? Based on Io’s orbital period (approximately 1.769 days), Ole Rømer observed that eclipses occurred 11 minutes earlier when Earth was closer to Jupiter and 11 minutes later when Earth was farther away. Using this time difference, he calculated that light takes 11 minutes to cross the diameter of Earth’s orbit around the Sun (approximately 186 million miles). From this, he estimated the speed of light to be about 220,000 kilometers per second. Ole Rømer stated that light takes 11 minutes to cross the diameter of Earth’s orbit. At that time, the distances of Earth’s orbit might not have been accurately calculated, but now we know them precisely, don’t we? Now, if we calculate using the correct measurements we know today, the speed of light comes to 460,606,060 m/s. This means one of these three must be wrong: Ole Rømer’s 11 minutes, the diameter of Earth’s orbit (304,000,000 km), or the speed of light (299,792,458 m/s). Which of these do you think is wrong?" Assuming that light travels at this speed (299,792,458 m/s) , it takes 16 minutes to cross the diameter of the Earth. But here the light has crossed in 11 minutes He may have been wrong about the speed of light or diameter of Earth’s orbit, but he had no chance of being wrong about time.

(~4.2 AU) When Earth is close to Jupiter → SD (~6.2 AU) When Earth is far from Jupiter ) → BD The time is yours, there must be an 11-minute difference. Now tell me your idea.

The second one is not finished yet. Let's not get distracted now. Let's finish the second thing first. Give everything a scale with a numerical score. It doesn't have to be exact. Just an average is enough. Only then can we make a decision about where to discuss.

In this picture, you know the time when the light started, but Rama didn't know that. He was in a place where he could receive the light. He could only see the light that was stopped by him and the light that was received again. Okay, now let’s imagine you are placed exactly in Ole Rømer’s position. Suppose you have been given the responsibility of discovering the travel time of light between Jupiter and Earth. Tell me step by step how you would find it. Let’s discuss it. (Anyone who believes light is delayed can do this too.)

The time interval between when light is stopped at a point and when it is received again

Your question doesn't seem to point out my mistake, I'll avoid repeating the answer I've already given. Nothing else. I have given you a map. That map is right in front of you. There are many features in it that you can study. Before you answer me, will you check whether what I have said is true or not? There are lines from 2 to 8 on it. There is a stopwatch on your phone. Use it to measure and tell me what difference you see. Okay, now let’s imagine you are placed exactly in Ole Rømer’s position. Suppose you have been given the responsibility of discovering the travel time of light between Jupiter and Earth. Tell me step by step how you would find it. Let’s discuss it. (Anyone who believes light is delayed can do this too.)

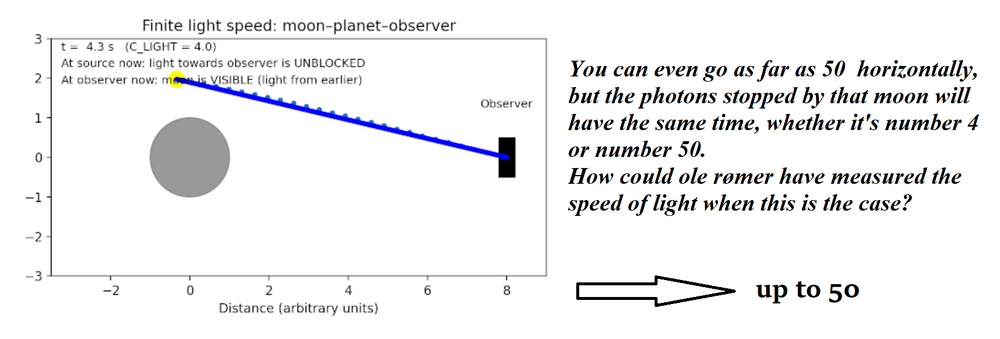
If light had the property you think it has, this is exactly how it would behave. This graph ends at 8; extend it to the right up to 100. No matter which number you pick between 4 and 100, the amount of time Jupiter blocks the light at that point will always be the same, because distance does not change the duration of the blocking. But what Ole Rømer observed was different. He started counting time from the moment Io disappeared. When Earth was very close to Jupiter, it took 2 hours and 10 minutes for Io to disappear and reappear. Six months later, when he recorded it again (with Earth on the opposite side of the Sun, very far from Jupiter), it took Io 2 hours and 21 minutes to disappear and reappear. He subtracted the first measurement from the second and said the remaining 11 minutes was the delay.

Okay, now let's talk in a different way. Instead of talking about how much time is delayed, let's talk about how much time it was visible. When Earth is close to Jupiter, for each full orbit of Io, Io was visible for 2,419 minutes. When Earth was far from Jupiter, for each full orbit of Io, Io was visible for 2,408 minutes. If, as you say, there is a delay, then the amount of time Io is visible should not change. The actual time for Io to complete one full orbit is 2,549 minutes. If, as you say, we measure using the first minute when Io becomes visible: When Earth is close to Jupiter, the time for Io to complete one full orbit becomes 2,549 minutes. When Earth is far from Jupiter, the time for Io to complete one full orbit becomes 2,559 minutes.

You can even go as far as 50 horizontally, but the photons stopped by that moon will have the same time, whether it's number 4 or number 50. How could ole rømer have measured the speed of light when this is the case?

It takes 2,549 minutes for Io to complete one orbit around Jupiter. Let us start from the moment Io disappears behind Jupiter. We will consider the exact minute when Io goes behind Jupiter as minute 1. We have a telescope pointed at Jupiter, and it takes one photo every minute. In the first 120 photos, Io is not visible because Io is behind Jupiter (we know this). When Earth is close to Jupiter , Io starts becoming visible again from the 130th photo onward. That is, out of the total 2,549 photos taken in one full orbit, Io is recorded in 2,419 photos. Six months later, when Earth is far from Jupiter , Io starts becoming visible only from the 141st minute. That is, out of the total 2,549 photos, Io is recorded in only 2,408 photos. 11 minutes of Io were visible — we ourselves are the witness. 11 minutes of Io were missing — we ourselves are the witness again. (Pay close attention to the 11 photos in this place. I'm not saying they arrived late, I'm saying they disappeared.) If you say that those same 11 minutes that were visible when Earth was close to Jupiter appear delayed when Earth is far away, you are effectively claiming that Io’s orbital period increases by 11 minutes every single orbit. That is impossible. When Io does not change its orbital period due to the delay of light. When Earth is close to Jupiter → Io reappears at position 2. When Earth is far from Jupiter → Io reappears at position 3. We call them light waves, we call them photons. Using these, how will you explain this phenomenon?

There's nothing wrong with using AI to confirm whether the event I'm telling you is false or not.

Ask an AI to confirm the truth.

It takes Io 1.77 Earth days (42 hours 29 minutes) or 2,548.8 minutes to complete one orbit around Jupiter. We know where Io is in these 2,548.8 minutes, including being behind Jupiter. Those minutes that disappeared after coming out are lost and will never be get again.

Io takes two hours to pass behind Jupiter. After that, all the remaining occulted times depend on the distance. That is, when Jupiter and Earth are close together, Io will be hidden by Jupiter for two hours. After those two hours, when Io comes out, it will be occulted again for about ten minutes (when there is nothing between Io and Earth), depending on the distance. Moreover, when Jupiter and Earth are very far apart, Io will be hidden by Jupiter for two hours, and additionally for about 20 minutes when there is nothing between Earth and Io. If we were perhaps watching from Neptune, Io would be hidden by Jupiter for two hours, and the remaining 4 hours would be occulted depending on the distance.

Ole Romer's study also says the same thing. He says that light was hidden for 11 minutes in addition to crossing the diameter of our Earth's orbit.

It takes Io 1.77 Earth days (42 hours 29 minutes) or 2,548.8 minutes to complete one orbit around Jupiter. If Earth is close to Jupiter, Io will be occulted for an average of 2 hours and 10 minutes. If Earth is far from Jupiter, it will be occulted for up to 2 hours and 20 minutes. When Jupiter and Neptune are on opposite sides of the Sun, Io will be occulted for 6 hours and 15 minutes when viewed from Neptune. During those four hours and 10minuts, what happens to the sunlight that normally falls on Io?

I can guess what all of you haven’t understood. If it doesn’t click for you immediately, there’s no mistake—it’s the very same thing that nobody understood for 350 years. If light had the properties you think it has, Ole Rømer would never have had any chance to measure its speed. Let me give an example with balls: Imagine you’re inside a room, and right above your head there’s a hole through which balls fall into a basket via a pipe. You’re inside the room. You tell your friend outside: “Throw a ball in every five minutes. The distance is up to you, but once you start throwing, don’t change your position.” You, inside the room, will see a ball arrive exactly every five minutes. Just from that, can you tell how far away he was when he sent the balls? Let’s look at it from another angle: You throw 10 balls toward me. If I tell you that the first four balls never reached me—they vanished on the way—how would that feel? That’s exactly what those eleven minutes are.