Ethan Every

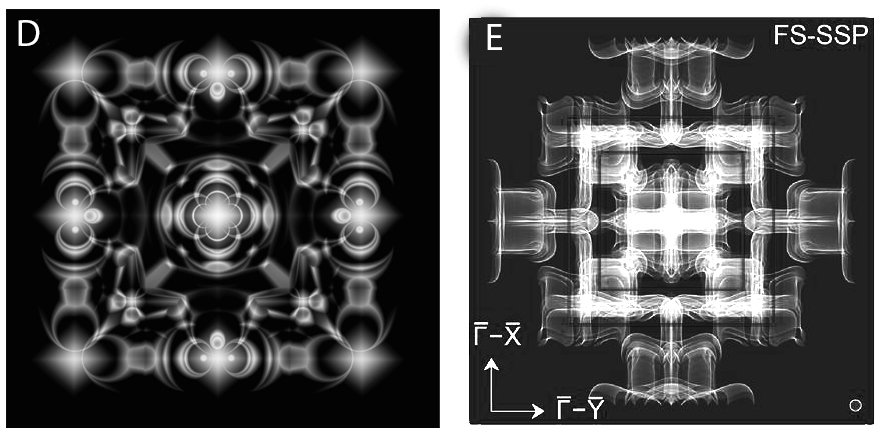
I’ve isolated the orbitals of the object as a whole (Ex D). The closest thing I’ve found to this structure is also interference based, in this case the object sort of resembles these Quasiparticle interference of TaAs surface states (Ex E, Ref A). The fresnel zone images emerge in a particular area of the interior of the object rather than on the surface which is why I’m having a difficult time defining the geometry of that particular space, but ultimately it emerges from the structure pictured here (ex D) . Looks like maybe sphere folding Ex E might give me something close to Ex D but I can only express that as code, I've no idea how that would be done in calculus at this point (Sphere or ball folding Ex F). Obviously my goal would be to translate the geometry of the object into something practically useful. Ref A : https://science.sciencemag.org/content/351/6278/1184?rss=1

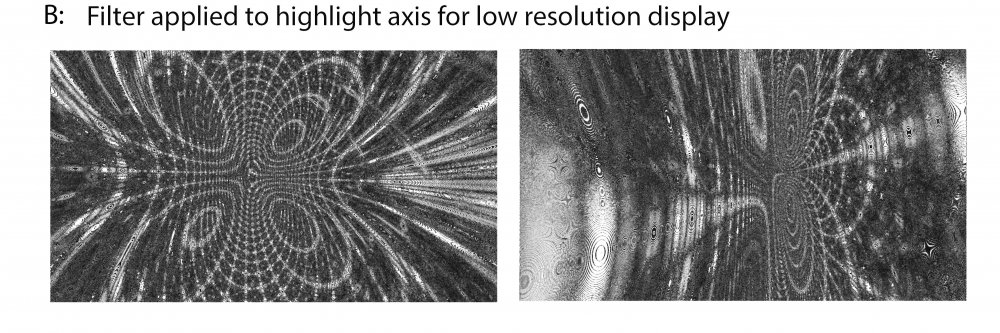
There are certainly significant similarities. The images I posted have an edge filter on to highlight the axis as they are difficult to identify with lower resolution photos. In a high resolution render (Ex. C) you can see the particulars of this model as it transitions from a traditional 2d representation of a fresnel zone out to the larger 3 dimensional space. The footage phases from frame to frame and produces some interesting overtones as the space becomes more defined. While the image changes depending on what percentage of your screen is used to display it there appear to be specific low interference axis that underlay the image at any scale, I'm trying to use these to define the geometry that produces the interference. Example C : https://mega.nz/file/5Ux0hDJa#HoppqGXb8m7dm1EQyj1jTmo-QYwmei7XwevLPpBhL_g

Thanks for the clarification! Although they look incredibly similar I wasn’t sure if it was appropriate to label the similar properties of this 3d object as fresnel zones because I am not deriving them the traditional way. Additionally as the field of vision gets broader than the first example I posted the object reveals some new characteristics that I’ve been apprehensive to label without verification (Ex. A). I’ve been attempting to define the geometry here so I can properly measure it but it’s difficult as it warps and lenses depending on how it is observed (Ex. B).

Yea its certainly not displaying any orbitals associated with massive particle. I guess I thought maybe it was related to massless objects like photons/light or other physical waves. Seems like maybe the similarity is from the juxtaposition of a flat axis surrounded by a curved surface in the 3d object, im guessing that just mimics the way a curved lense interacts with light rays or other waves. Still I suppose its interesting to create interference like that with a single mathematical object rather than multiple interacting elements. Maybe i'll find some useful application for it. Thanks for the feedback

So would it make sense to presume some version of the schrodinger equation is present in this structure or can we make these fringes a bunch of ways?

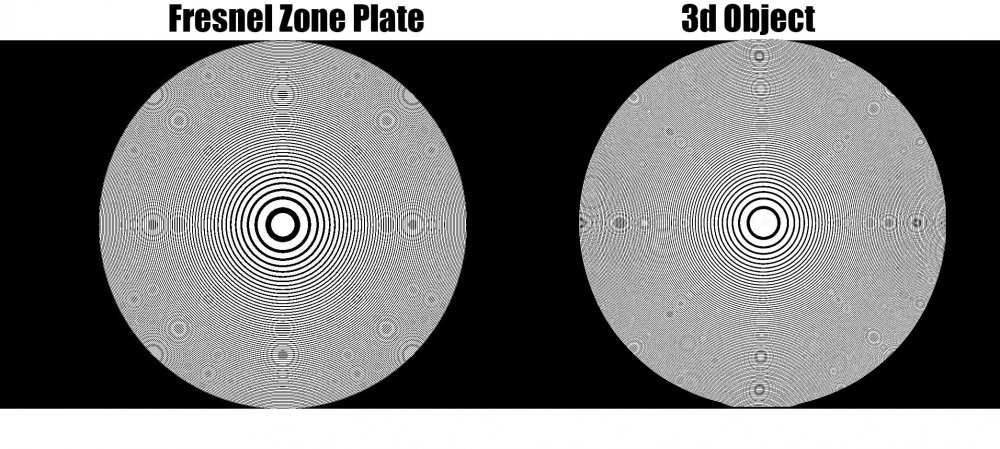
I’ve been wondering about the significance of generating interference fringes of 3d representations of “fresnel zones”. Would the parameters used in generating high res fresnel zones be useful in describing wave functions in the same way an actual zone plate would be? It's hard to imagine the math in the code wouldn’t be in some way related to the actual physical phenomena if the result is visually identical, but perhaps I’m mistaken. I’ve been exploring a 3d object and stumbled upon some emergent interference fringes (the fringes are not programmed intentionally) and I’m wondering if that means the object could be useful for modeling waves, wave interactions etc. Here’s some examples of what I mean, I’d be grateful for any feedback. Thanks

Heres the easiest way I can summarize this idea: My wording will general here. Many physicists believe that all the forces unified in a singularity before the big bang. There's an assumption that whatever that primal state is it has some infinite dimension allowing it to avoid the necessity of an external cause as well as some finite dimension allowing for a potential non-uniform distribution of energy. Perhaps if we would like to model what’s inside that singularity we could use a unified structure with some infinite points and some finite points. If this structure could also recreate the properties we observe in our physical reality as emergent properties we might have some additional explanation for the trend toward complexity. Time escape folding fractals have some points that extend to infinity and some that do not and the mandelbox specifically is capable of replicating a number of complex properties including the geometries of photons found in quantum holography from a variety of perspectives, interference based reconstruction of fresnel lense zone plates, aberrated zone plates, gravitational lensing, diffraction and a miriad of other properties. I’m suggesting this is a model worth exploring when discussing basic structures. Thanks all for the feedback, I'll have formalized versions of all this in a few months and will update as soon as I do. Cheers

I’ve seen folding space most often referenced in physics regarding einstein-rosen bridge (theoretical wormholes) and more recently the ideas wormed their way (pun intended) into some explorations of quantum tunneling and entanglement (https://arxiv.org/pdf/1604.02589.pdf for example). Tom Lowe said regarding the Mandelbox “Since escape-time fractals need some points that do not escape to infinity and some points that do, it follows that the way to provide this is to fold space on top of itself and then enlarge it”. This seemed like an intriguing way to model how information might interact with singularities, entanglement, tunneling etc. In a general sense I’m interested in the possibility that any constant in a complex system (like the speed of light in the physical universe) might be expressed as a geometry and that this structure may act as an attractor on the evolution of the system. Physics and light seem like a great domain to test these ideas because not only do we have the interaction of a constant with a complex system but advances in simulation and visual detection through quantum holography may make successful models easy to identify. Attractors in other systems are often buried under layers of abstraction and are rarely visible as isolated objects in the system as observed. The Mandelbox has an interesting relationship with scale. Unlike the mandelbrot set zoom and scale don’t replicate the geometry of the previous render. I’ve prepared some visuals to illustrate the point. Here I use the 1st iteration Mandelbox where the geometry is easiest to identify. With the software I use here it seems to have 3 distinct phases related to scale: -3 to 0, 0 to 1, and 1 to 5. 0 to 1 has some interesting properties. 0 to 1 has some interesting properties. As the scale increases the center sphere projects fringe lobes away from the center as the interference pattern in the center increases in frequency. Throughout that transformation the center sphere extends resembling (though with obvious distinctions) a sphere with chaotic geodesic flow which is the first known example of a sphere in 3 dimensions whose geodesic flow is chaotic (Image on right created by Bryn Mawr math major Louisa Winer using Mathematica, Surface Evolver and Geomview.) At 1 beams along the axis extend and a container like object encompasses the previous state, this is reversed with rot angle 180. Specifically regarding the entangled like representation found within the object an increase in scale presents 3 successive representations of the geometry while an external view of that transformation shows a flickering interference pattern, I've uploaded videos of these transformations that contain much more information in the transformations. If there is a dm option you can ask for a link as we're not allowed to post to external links

Well put, I'll continue to put some time into this and hopefully have something more substantial to offer next time. Thanks

Agreed! Thanks for the feedback. I agree about the explanation being the most important part, thats a much longer process I'm working on. Among other things at this point I've noticed the Fresnel lense distortion that appears to be recreated is a direct result of the folded geometry, in fact basic diffraction/interference patterns emerge in the simplest iteration of the fractal which is encouraging. However in higher iterations it appears capable of modeling a large variety of phase diagrams. - a simple illustration of a little phase fluctuation Aside from the the textbooks, any ideas on formulating emergence? That's the real headache... goodness

I see. Well perhaps not. Actually what interested me in fractals in the first place was that the way they deal with infinities, I hoped they might answer some identity problems in the philosophical world . I assume there are a wide variety of fractal representations that might be useful for modeling physical objects. What I'm hoping is that the folded geometry of the mandelbox may shed some light (pun intended) on a possible structure of light, I'm exploring the idea that it's properties are perhaps emergent from a folded geometry. Thanks for the feedback, I'm getting into the nitty gritty work on it. Perhaps I got a little over excited and shared the preview prematurely

Certainly. In fact I've had zero success representing any of these objects with Kalibox, mandelbulbs etc. Although I've been able to generate interference patterns in some of these large scale properties like lensing never materialized. What I find compelling about the mandelbox specifically is the simple way it models folding and the fact that 1st iteration representations of the fractal can replicate the rather specific geometries of photons from multiple perspectives.

There are plenty of physicists arguing that the geometry of spacetime is folded. This model is largely in support of those views, being able to recreate a large variety of these properties with a single fractal is what I find interesting I'm aware of the gaussian similarity, however in this case the internal view of the mandelbox fractal has orbitals that are in the same position as the representations in the entangled photon state. In addition the external view of the low iteration mandelbox fractal is capable of recreating the geometry found in the single photon hologram shown above.

I'd insert the link to the article if I could The images are of the mandelbox fractal Thanks for the feedback btw

na