butovsv

The immutability of a human impulse is the immutability of a zero human momentum. And the immobility of the Varipend systems looks like this: The total momentum of this system is zero. You can try to depict this system with a constant CM and a constant total momentum. You won’t succeed.

The center of the mass system of bodies is a function of 2 (two) time-dependent variables. [math]{{\vec R}_c}(t) = \frac{{\sum {{m_i}(t){r_i}(t)} }}{{\sum {{m_i}} (t)}}[/math] The velocity of the Center of Mass is a derivative of the radius vector: [math]{v_c}(t) = \frac{{d{R_c}(t)}}{{dt}} = \frac{{\sum {{m_i}{{\dot r}_i}(t)} }}{{\sum {{m_i}} }} + \frac{{\sum {{{\dot m}_i}{r_i}(t)} }}{{\sum {{m_i}} }}[/math] If you want to know the antiderivative of a function, try to integrate the derivative of this function: [math]{R_c}(t) = \int {{v_c}(t)} dt = \int {\left( {\frac{{\sum {{m_i}{{\dot r}_i}(t)} }}{{\sum {{m_i}} }} + \frac{{\sum {{{\dot m}_i}{r_i}(t)} }}{{\sum {{m_i}} }}} \right)} dt = \int {\left( {\frac{{\sum {{m_i}{{\dot r}_i}(t)} }}{{\sum {{m_i}} }}} \right)} dt + \int {\left( {\frac{{\sum {{{\dot m}_i}{r_i}(t)} }}{{\sum {{m_i}} }}} \right)} dt[/math] The radius vector of the CM of the system of bodies is the result of the addition of two "vectors" - the radius vector of inertial displacement and the pseudovector of deformation of the system of bodies.

F=ma It is very, very, very, very WRONG. Have I explained in sufficient detail? What is the failure of my answer? The total momentum of this system is zero. There is no other solution to the balance of the total momentum of this system! But if you see with your own eyes the center of mass of this system, you see how the CM moves, violating the laws of conservation, then this is exclusively your personal problem! This beautiful task should not be sent to the "trash can". You need to throw your naive childish sensations of "banal physics" into the basket! The knowledge "twice two is always four" is very good knowledge! Right! But it will not help in extrapolating the function of the CM of the system of bodies in which the parts change masses!

I apologize! I have said this many times already! The center of Mass is not a material object! The CM does not have mass! Newton’s second law cannot be applied to the Center of Mass! The Mass Center is calculated as follows: [math]{{\vec R}_c}(t) = \frac{{\sum {{m_i}(t){r_i}(t)} }}{{\sum {{m_i}} (t)}}[/math] But like this: [math]{{\vec R}_c}(t) = {{\vec R}_c}(0) + {{\vec V}_c}(t)t + \frac{1}{2}\frac{{{{\vec F}^e}}}{M}{t^2}[/math] coordinates of a single material body with mass are calculated. Whatever the total mass is. This is your example. I don't know the value. Stop stalling and answer the questions that have been asked of you.  Here are the coordinates of the Mass Center of a certain system: [math]\vec R = \frac{{\sum {{m_i}{{\vec r}_i}} }}{{\sum {{m_i}} }} = \frac{{{m_1}{{\vec r}_1} + {m_2}{{\vec r}_2} + {m_3}{{\vec r}_3} + ... + {m_i}{{\vec r}_i}}}{{{m_1} + {m_2} + {m_3} + ... + {m_i}}}[/math] Please help me find the "total mass." That "total mass", which cannot move in any way without the "acceleration" caused by "external force"! The unit of measurement of the Center of Mass of the system of bodies is the unit of length of the selected Reference System. Meters, feet, inches, elbows, yards, miles ..... I would be very grateful to you, “atomic clock specialist,” if you would explain to me, deeply illiterate, how to apply Sir Newton’s second law to “miles”. Thank you in advance!

Your attempts would not be permissible for a student who wished to pass their course. Then correct your phrase! Just take it and write the Tsetra Mass equation of the system of bodies! And look at what this value depends on! In order not to disgrace ....

F=ma And what is the mass of the "Center of the Mass of the system of bodies" equal to?

Still wrong. hM-m..... It's good that you are literate - you all know! You know where the truth is, and where the lie! Watch attentively! Law of Conservation of Momentum The law of conservation of momentum states that the vector sum of the momenta of all the bodies of the system is constant if the vector sum of the external forces acting on the system of bodies is zero. In the language of mathematics, this law is written like this: [math]\vec P(t) = \sum {{m_i}(t){{\dot r}_i}(t)} = const[/math] [math]\frac{{d\vec P(t)}}{{dt}} = \frac{{d(\sum {{m_i}(t){{\dot r}_i}(t)} )}}{{dt}} = \sum {{m_i}{{\ddot r}_i}} + \sum {{{\dot m}_i}{{\dot r}_i}} = 0[/math] If: [math]\frac{{d\vec P(t)}}{{dt}} = \frac{{d(\sum {{m_i}(t){{\dot r}_i}(t)} )}}{{dt}} = \sum {{m_i}{{\ddot r}_i}} + \sum {{{\dot m}_i}{{\dot r}_i}} \ne 0[/math] - this means that the system is "affected by external forces." Do you know what these "external forces" are, dear "atomic clock specialist?" They are equal to this: [math]{{\vec F}^e} = \frac{{d\vec P(t)}}{{dt}} = \frac{{d(\sum {{m_i}(t){{\dot r}_i}(t)} )}}{{dt}} = \sum {{m_i}{{\ddot r}_i}} + \sum {{{\dot m}_i}{{\dot r}_i}} [/math] This is Physics. The science is ....

Is that not enough?

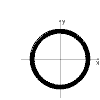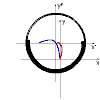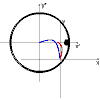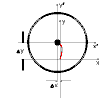
I beg your pardon if I did not answer any question. Ready to answer any question! There are no secrets! True?! [math]\vec F = \frac{{{\rm{d}}\vec p}}{{{\rm{d}}t}} = \frac{{d(m\vec v)}}{{dt}} = m\frac{{d\vec v}}{{dt}} = m\vec a[/math] Something is wrong? Butov did not study well at school ?! In general, the change in momentum looks like this: [math]\vec F = \frac{{{\rm{d}}\vec p}}{{{\rm{d}}t}} = \frac{{d(m\vec v)}}{{dt}} = m\frac{{d\vec v}}{{dt}} + {{\vec v}_r}\frac{{dm}}{{dt}} = m\vec a + {{\vec F}^{jet}}[/math] And, once again, you have failed to explain what is going on in your diagrams, that people might have a chance to make some sense out of them. I will show how the Mass Center of the Varipend system is calculated: [math]{r_c}(t) = \frac{{{m_{liquid}}(t){r_1}(t) + {m_{case}}(t){r_2}(t)}}{M}[/math] In order to calculate the coordinates of the CM system at any time, it is necessary to know the masses and coordinates of the parts of the system. And the masses and coordinates of the parts of the system change over time. These CHANGES are subject to conservation laws: the Law of Conservation of Momentum and the Law of Conservation of Energy. In order to calculate the coordinates of the system at any time , it is enough to solve the differential equation of the momentum balance of the parts of the system: [math]{p_{var}}(t) = {m_{liquid}}(t){{\vec v}_1}(t) + {m_{case}}(t){{\vec v}_2}(t)=0[/math] Oh! Or maybe you want to solve the differential equation of a "brick" of the same mass as the Varipend system? [math]{m_{brik}}{{\vec v}_{brik}} = 0[/math] Because there is a very respectable competent reason for this - is this equation a little easier?

Nothing complicated! The device shows you the Law of Conservation of Momentum. In your head is the "Mechanics of the material body." [math]{{\vec R}_c}(t) = {{\vec R}_c}(0) + {{\vec V}_c}(t)t + \frac{1}{2}\frac{{{{\vec F}^e}}}{M}{t^2}[/math] And nothing but this! But I explain to you the Mechanics of the system of bodies. I remind you that the Mass Center of the body system is not a material object. [math]{{\vec R}_c}(t) = \frac{{\sum {{m_i}(t){r_i}(t)} }}{{\sum {{m_i}} (t)}}[/math] The result of the CM function is not subject to the laws of conservation, because it does not have mass. Let's! The graph of the total momentum, that is, the momentum of the entire system, coincides with the abscissa of the graph. If at any moment in time the relative motion of the system of moving elements ceases, the entire mechanical system will have an initial velocity. If at the initial moment of time the whole mechanical system had zero velocity in the system ... then after stopping the system of moving elements the velocity of the entire mechanical system will also be zero! Graph of the overall momentum of the system. Moving the Varipend system can be called a "linear precession". This movement is inertialess. The total momentum of the system and the kinetic energy of the entire system, reduced to the CM of the system, are zero. At every moment in time, the system is formally motionless. The system does not have inertia to continue moving. In order for the system to move rectilinearly and evenly - it is necessary to expend energy. Did you notice that pesky little "dt" in those equations? What are the fundamental units of force? Of momentum? Are they equal?  Of course! Add! [math]{{\vec F}_1} = {{\vec F}_2}[/math] [math]\frac{{{\rm{d}}{{\vec p}_1}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}{{\vec p}_2}}}{{{\rm{d}}t}}[/math] This is Physics. The science is ...

Look in every physics textbook or for example the barycentre for the Earth Sun system. The Centre of mass is off centre of the sun due to the gravitational force of attraction of other planets such as Jupiter If you wish confirmation study Kepler's laws. The centre of mass is always the vectoral sum of forces. From your own link Choose a reference point R in the volume and compute the resultant forceand torque at this point, what do you think a resultant force is ? "Resulting force" is the change in the total momentum of a mechanical system. Write the dependence of the "center of mass of the system of bodies" on the "resulting force". All equations in this branch are given in vector form. I cannot give a calculation in the projections of vectors on the axis of the corresponding coordinates here. Very little space. I can give a link to these calculations! ! Moderator Note Dr Swanson is a working atomic physicist, not a "layman". His atomic clocks help regulate our global GPS system. Perhaps you should examine your own failings instead. Please focus on answering some of the questions you've been asked, and leave the professional qualifications out of it. It's clear you need some help with your concept, and you won't get it by rejecting mainstream physics. Focus on the details of your idea, and stop trying to teach physics.  A very serious argument! And I am a specialist in powerful technological lasers. But we will not talk about lasers here! I hope that after Dr Swanson remembers the basic concepts of Mechanics, his "atomic clock" will work even better! "Dr Swanson" wrote: Such a phrase is permissible for a student. But VERY embarrassing for an "atomic clock specialist"!

Oh?! "Force" = "change in momentum" [math]\vec F = \frac{{{\rm{d}}\vec p}}{{{\rm{d}}t}} = \frac{{{\rm{d}}\left( {m\vec v} \right)}}{{{\rm{d}}t}}[/math] This is Physics. The science is ... Bad answer. The response of the layman. I repeat again. Watch and read carefully. Material Point System: The total momentum of this point system is defined as follows: [math]\vec P = \sum {{{\vec p}_i}} = \sum {{m_i}{v_i}} = {m_1}{{\vec v}_1} + {m_2}{{\vec v}_2} + {m_3}{{\vec v}_3} + ... + {m_i}{{\vec v}_i}[/math] If all these points would have the same speed, then this speed could be taken out of the sign of the sum, and sum the mass: And it would turn out like this: [math] \ vec P = M {\ vec V_c} [/math] In order for the speeds of all points of the system to become equal, all these points need to be simply connected! Connect inelastically! [math]{m_1}{{\vec v}_1} + {m_2}{{\vec v}_2} + {m_3}{{\vec v}_3} + ... + {m_i}{{\vec v}_i} \to Boom!!! \to ({m_1} + {m_2} + {m_3} + ... + {m_i}){V_c} = M{V_c}[/math] Actually, what you schoolchildren only know how to do! .... But here is the misfortune in this "simple" task .... As the author of this task, I came up with an inelastic connection of system components according to a special law. Like this: And in the total momentum for this system, the following regularity was determined: [math]{m_1}{{\vec v}_1} + {m_2}{{\vec v}_2} + {m_3}{{\vec v}_3} + ... + {m_n}{{\vec v}_n} = ({m_{i1}} + {m_{i2}} + {m_{i3}} + ... + {m_{in}}){{\vec V}_{ic}} + ({m_{k1}} + {m_{k2}} + {m_{k3}} + ... + {m_{kn}}){{\vec V}_{kc}}[/math] And what is very curious - the masses of particle systems with the same velocity (i.e. material points, material bodies!) - are constantly changing! Look: [math]{m_1}{{\vec v}_1} + {m_2}{{\vec v}_2} + {m_3}{{\vec v}_3} + ... + {m_n}{{\vec v}_n} = ({m_{i1}} + {m_{i2}} + {m_{i3}} + ... + {m_{in}}){{\vec V}_{ic}}({t_1}) + ({m_{k1}} + {m_{k2}} + {m_{k3}} + ... + {m_{kn}}){{\vec V}_{kc}}({t_1})[/math] [math]{m_1}{{\vec v}_1} + {m_2}{{\vec v}_2} + {m_3}{{\vec v}_3} + ... + {m_n}{{\vec v}_n} = ({m_{i1}} + {m_{i2}} + {m_{i3}} + ... + {m_{in - 1}}){{\vec V}_{ic}}({t_2}) + ({m_{k1}} + {m_{k2}} + {m_{k3}} + ... + {m_{kn + 1}}){{\vec V}_{kc}}({t_2})[/math] [math]{m_1}{{\vec v}_1} + {m_2}{{\vec v}_2} + {m_3}{{\vec v}_3} + ... + {m_n}{{\vec v}_n} = ({m_{i1}} + {m_{i2}} + {m_{i3}} + ... + {m_{in - 2}}){{\vec V}_{ic}}({t_3}) + ({m_{k1}} + {m_{k2}} + {m_{k3}} + ... + {m_{kn + 2}}){{\vec V}_{kc}}({t_3})[/math] Therefore, the total momentum of the entire system as a whole can be written as follows: [math]{p_{var}}(t) = {m_{liquid}}(t){{\vec v}_1}(t) + {m_{case}}(t){{\vec v}_2}(t)[/math] And this total momentum cannot change without an external energy source. This is the Law! Called: Law of Conservation of Momentum. [math]{p_{var}}(t) = {m_{liquid}}(t){{\vec v}_1}(t) + {m_{case}}(t){{\vec v}_2}(t)=const=0[/math] if [math]{{\vec F}^e} = 0[/math] Can anyone solve this differential equation? Or is it not necessary to solve it, because instead of this equation it is possible to solve the "brick equation" easily, even in the mind? [math]{{\vec R}_c}(t) = {{\vec R}_c}(0) + {{\vec V}_c}(t)t + \frac{1}{2}\frac{{{{\vec F}^e}}}{M}{t^2}[/math] Just because this equation is much simpler and more understandable to any student? Write this mathematical dependence, "a connoisseur of physics"! Write, please! I really hope that I will be able to explain to you what Real Physics is.

No! Where did you see the dependence of the Center of Mass on "forces" ?!

If brick 1 (one), then the path of the brick is determined like this: [math]{{\vec R}_c}(t) = {{\vec R}_c}(0) + {{\vec V}_c}(t)t + \frac{1}{2}\frac{{{{\vec F}^e}}}{M}{t^2}[/math] If inside the brick, “something” “somewhere” moves relative to the brick For example, like this: Then the Mass Center of such a "brick" is calculated like this: [math]{r_c}(t) = \frac{{{m_{liquid}}(t){r_1}(t) + {m_{case}}(t){r_2}(t)}}{M}[/math] Yes! Parts of the system can interact! Their pulses can change in very large limits! They can accelerate and slow down! But at the same time, the total momentum of the system remains unchanged. The force is not the change in momentum.  oh wow ..... You do not confuse Mechanics with "Star Wars": "May the force be with you"? Let's look at the ABC book? In Mechanics - just like that and no other way! Are we talking about Mechanics here? Why do you have a variable called mliquid? You described this as a pendulum, and have not said anything about a liquid.  good question... Material Point System: The total momentum of this point system is defined as follows: [math]\vec P = \sum {{{\vec p}_i}} = \sum {{m_i}{v_i}} = {m_1}{{\vec v}_1} + {m_2}{{\vec v}_2} + {m_3}{{\vec v}_3} + ... + {m_i}{{\vec v}_i}[/math] If all these points would have the same speed, then this speed could be taken out of the sign of the sum, and sum the mass: And it would turn out like this: [math] \ vec P = M {\ vec V_c} [/math] In order for the speeds of all points of the system to become equal, all these points need to be simply connected! Connect inelastically! [math]{m_1}{{\vec v}_1} + {m_2}{{\vec v}_2} + {m_3}{{\vec v}_3} + ... + {m_i}{{\vec v}_i} \to Boom!!! \to ({m_1} + {m_2} + {m_3} + ... + {m_i}){V_c} = M{V_c}[/math] Actually, what you schoolchildren only know how to do! .... But here is the misfortune in this "simple" task .... As the author of this task, I came up with an inelastic connection of system components according to a special law. Like this: And in the total momentum for this system, the following regularity was determined: [math]{m_1}{{\vec v}_1} + {m_2}{{\vec v}_2} + {m_3}{{\vec v}_3} + ... + {m_n}{{\vec v}_n} = ({m_{i1}} + {m_{i2}} + {m_{i3}} + ... + {m_{in}}){{\vec V}_{ic}} + ({m_{k1}} + {m_{k2}} + {m_{k3}} + ... + {m_{kn}}){{\vec V}_{kc}}[/math] And what is very curious - the masses of particle systems with the same velocity (i.e. material points, material bodies!) - are constantly changing! Look: [math]{m_1}{{\vec v}_1} + {m_2}{{\vec v}_2} + {m_3}{{\vec v}_3} + ... + {m_n}{{\vec v}_n} = ({m_{i1}} + {m_{i2}} + {m_{i3}} + ... + {m_{in}}){{\vec V}_{ic}}({t_1}) + ({m_{k1}} + {m_{k2}} + {m_{k3}} + ... + {m_{kn}}){{\vec V}_{kc}}({t_1})[/math] [math]{m_1}{{\vec v}_1} + {m_2}{{\vec v}_2} + {m_3}{{\vec v}_3} + ... + {m_n}{{\vec v}_n} = ({m_{i1}} + {m_{i2}} + {m_{i3}} + ... + {m_{in - 1}}){{\vec V}_{ic}}({t_2}) + ({m_{k1}} + {m_{k2}} + {m_{k3}} + ... + {m_{kn + 1}}){{\vec V}_{kc}}({t_2})[/math] [math]{m_1}{{\vec v}_1} + {m_2}{{\vec v}_2} + {m_3}{{\vec v}_3} + ... + {m_n}{{\vec v}_n} = ({m_{i1}} + {m_{i2}} + {m_{i3}} + ... + {m_{in - 2}}){{\vec V}_{ic}}({t_3}) + ({m_{k1}} + {m_{k2}} + {m_{k3}} + ... + {m_{kn + 2}}){{\vec V}_{kc}}({t_3})[/math] Therefore, the total momentum of the entire system as a whole can be written as follows: [math]{p_{var}}(t) = {m_{liquid}}(t){{\vec v}_1}(t) + {m_{case}}(t){{\vec v}_2}(t)[/math]