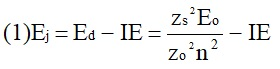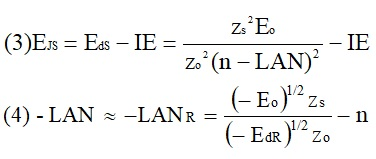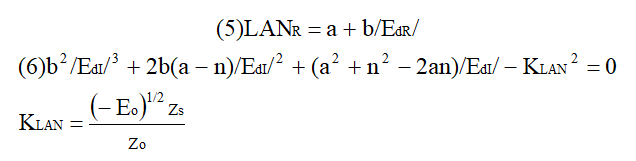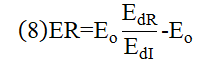Javier Silvestre

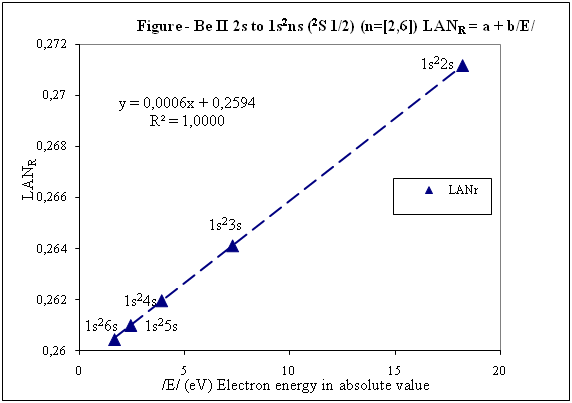
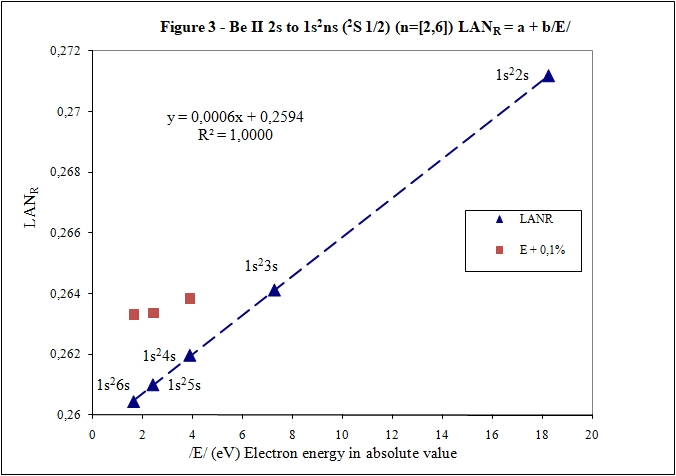
What "reference data"? This sounds an awful lot like a fudge factor, to make your theory align with experiment. National Institute of Standards and Technology (NIST) is not on the list of organizations created to do fudge factor Reference data included in these posts is consulted in NIST. z0 and zs is nuclear charge of this theory and is the net positive charge experienced by an electron in atom. For this reason (positive charge) is with positive sign in this introduction. A complicated value of this nuclear charge (such as that of effective nuclear charge) could be associated with a trick to make this theory seem correct. This fact does not happen since the nuclear charge of this theory is very simple to know for calculations of LANR factor. In first post there is an example: And in the last post there are 4 examples. In these 4 examples are charge values (z0 and zs), ionization energies of the electron 1s and excited electron. For example: n is the main quantum number where excited electron is and whose associated energy (Es) is included in LANR factor formula. LANR factor is also interesting to calculate for ground state in jumps ns → n's because is the only case where ground state meets linearity of LANR vs. Energy of the excited electron (this is one of LANR properties) and can be checked in Figures 2 and 3 of the previous post. Yes, correct, as you are calculating LAN factor for 2P state, n is 2. I have seen that LANR factor you have calculated (0.85) is very high for Hydrogen and it is because there is an error. Energy that must be included to calculate LANR factor is energy of excited electron and not energy required to pass from 1s (ground state) to 2p. LANR vs. Enery is a linear relationship of high sensitivity to energy variations and for this reason energy data to be entered to calculate LANR must be more precise, with more decimal places. For that lack of decimals, result is 0 with energies that you have indicated and it is not exactly 0. For this high sensitivity is a tool that provides energy data of excited states with precision. Hydrogen is as simple as the rest. Hydrogen is included in following steps that I will explain, but I want LANR calculation and linearity of LANR vs. Energy of excited electron are well understood previously. These are important points to be able to continue with this explanation. Whoever wants to can calculate LANR and check linearity of LANR vs. Electron energy excited for any of the 5 examples of the previous post with NIST data (data are online on NIST website). For example, I fully develop one of them: Example Beryllium Be II: 2s → 1s2ns (2S 1/2) (n=[2,4]) Positive charge experienced by electrons in Beryllium: Spectrum name Electron zs Be I 2s2 1 Be II 2s 2 Be III 1s2 3 Be IV 1s zo = 4 zs = 2 because is going to be studied Be II zo Beryllium is 4 (zo is always equal to its atomic number) Charges that I have just commented together with ionization energies of electron 1s and electron 2s contributed by NIST data: E (eV) zs Be II Eo (1s) (eV) zo (1s Be) -18,21115 2 -217,7185843 4 Energies compiled in NIST data are energies necessary to reach excited state. With ionization energy, energy that electron has in each excited state is easily obtained. Electron energies in absolute value /E/ in eV for each n are: n Configuration /E/ (eV) 2 1s22s (ground state) 18,21115 3 1s23s 7,2717868 4 1s24s 3,895384 5 1s25s 2,423607 6 1s26s 1,652262 n Configuration X Axis /E/ (eV) Y Axis LANR 2 1s22s (ground state) 18,21115 0,27118282 3 1s23s 7,2717868 0,26411911 4 1s24s 3,895384 0,26197142 5 1s25s 2,423607 0,26100057 6 1s26s 1,652262 0,26044400 Any questions, please consult. If everything goes well explained, I will continue. Thank you. Have a good day.

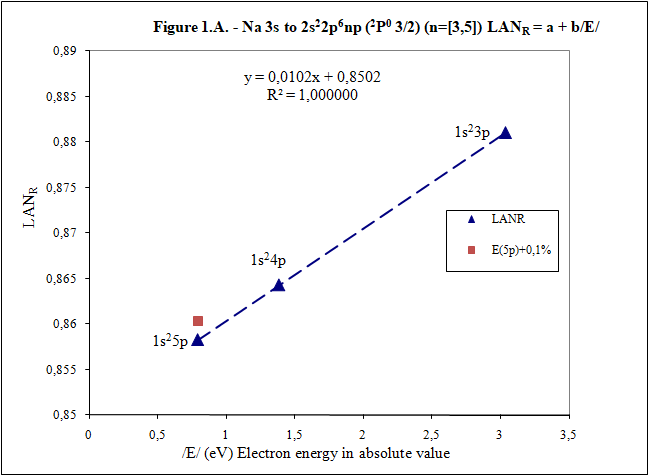
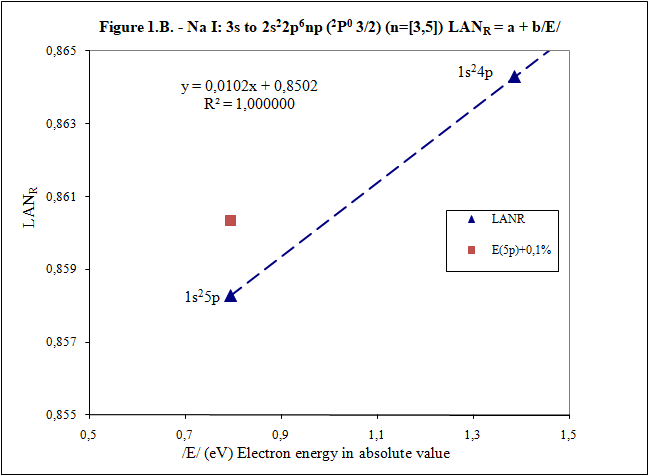
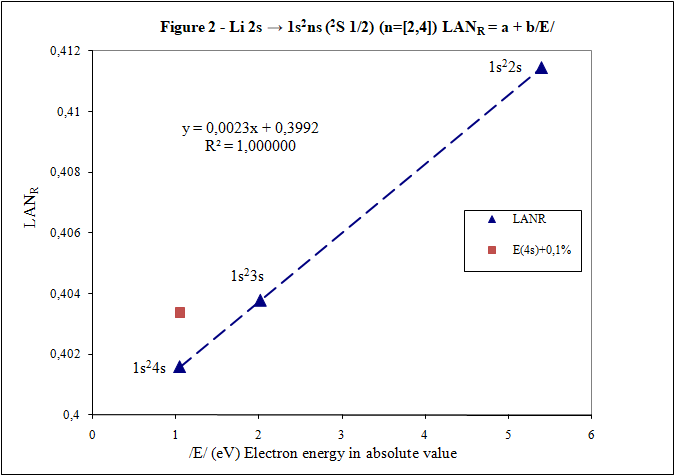
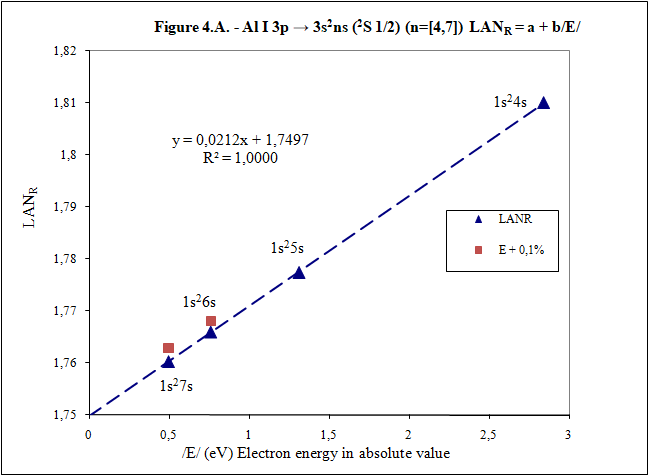
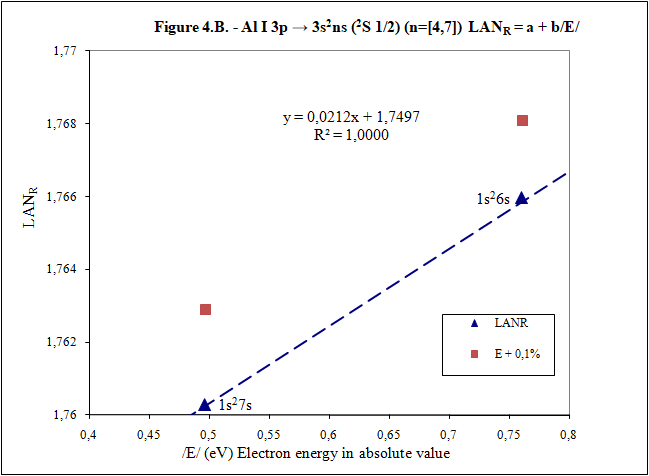
Thank you for your answers What is main conclusion of this introduction? Energy of excited electron (E) as increases n fulfills linear equation with LAN factor. That is, there is a relation type y = a + bx between energy of excited electron (E) and LAN factor (1): (1) LAN = a + b /E/ Note: Energy of excited electron has been indicated in absolute value in (1) (/E/) to be represented in first quadrant of representations LAN vs. Electron energy. How important can this lineal representation LAN vs. Electron energy? In addition to the importance of having and studying a linear relationship (such as V = IR), this linear relationship is fulfilled by every atom and excited state. Two facts can be highlighted: 1) This linear relation allows to calculate energy of excited electron 2) LAN factor of different atoms and different excited states are related to each other. This fact allows having another tool for assigning energy lines of excited states. What is LAN? LAN is an easily calculable factor for each excited state and depends mainly on quantum numbers l and n (hence its name, l and n, LAN). How can I calculate LAN factor for any excited state? LAN depends on energy and charge of excited electron and first electron in every atom that is electron 1s (2). Data that will be used to calculate LAN (2) are those provided by reference data in order to check whether, according to the reference data, linearity between energy of excited state and LAN factor is fulfilled (1). Therefore, LANR is LAN with reference data. Eo Ionization energy of electron 1s zo 1s electron charge (equal to atomic number) zs Start charge of excited electron E Energy of excited electron Examples to check linearity between energy of excited electron and LAN Linearity between energy of excited electron and LAN is going to be proven with several examples where different atoms and excited states are used. Initial notes: * Although LAN vs. Energy of excited electron is not the best representation to detect errors, deviations of 0.1% from reference data of energy of excited electron are also included to check sensitivity of this representation. * Reference values with lower n are used for these representation. Highest n values can also be represented by linearity, but point 4) of initial post must be considered, especially when atomic number is not low. Example 1: Sodium Na I: 3s → 2s22p6np Table 1. Reference data for Na I: 3s → 2s22p6np (2P0 3/2) (n=[3,5]) LANR = a + b/E/ E (eV) zs Na I Eo (1s) (eV) zo (1s) -5,1390769 1 -1648,70218 11 n /E/ (eV) LANR LANR with E(5p)+0,1% 3 3,034647716 0,88103258 4 1,3857554 0,86429549 5 0,7943173 0,85827356 E(5p)+0,1% 0,7951116 0,860342874 Example 2: Lithium Li I: 2s → 1s2ns (2S 1/2) (n=[2,4]) Table 2. Reference data for Li I: 2s → 1s2ns (2S 1/2) (n=[2,4]) LANR = a + b/E/ E (eV) zs Li I Eo (1s) (eV) zo (1s) -5,39171495 1 -122,454358 3 n /E/ (eV) LANR LANR with E(4s)+0,1% 2 5,391715 0,4114444 3 2,018586 0,4037755 4 1,050773 0,4015835 E(4s)+0,1% 1,051824 0,4033814 Example 3: Beryllium Be II: 2s → 1s2ns (2S 1/2) (n=[2,4]) Table 3. Reference data for Be II: 2s → 1s2ns (2S 1/2) (n=[2,6]) LANR = a + b/E/ E (eV) zs Be II Eo (1s) (eV) zo (1s) -18,21115 2 -217,7185843 4 n /E/ (eV) LANR LANR with E(xs)+0,1% 2 18,21115 0,27118282 3 7,2717868 0,26411911 4 3,895384 0,26197142 5 2,423607 0,26100057 6 1,652262 0,26044400 E(4s)+0,1% 3,899279 0,26383904 E(5s)+0,1% 2,426031 0,26336830 E(6s)+0,1% 1,653914 0,26331162 Example 4: Aluminum Al I: 3p → 3s2ns (2S 1/2) (n=[4,7]) Table 4. Reference data for Al I: 3p → 3s2ns (2S 1/2) (n=[4,7]) LANR = a + b/E/ E (eV) zs Al I Eo (1s) (eV) zo (1s) -5,985769 1 -2304,14005 13 n /E/ (eV) LANR LANR with E(xs)+0,1% 4 2,8430478 1,8101266 5 1,3128781 1,7774558 6 0,7605280 1,7659744 7 0,4966001 1,7602848 E(6s)+0,1% 0,7612885 1,7680898 E(7s)+0,1% 0,4970967 1,7629027 Additionally, example of Helium: 1s2 → 1sns (Term=3S J=1) can be seen in first post. Many more examples can be included, but I think they are enough to demonstrate existence of linearity between LAN and energy of excited electron. I have focused on an important part of first post to try to clarify it. Is it better this way? Thank you

Good Morning It may be that information is missing and is somewhat complex to understand also because of its novelty. I have tried to summarize to meet their rules: 2. Huge "walls of text" are usually difficult to get through and discourage participation. Present an abstract - a distillation of your idea first. Get into the details afterwards. I apologize if it was my fault. Anyway, there are questioned aspects that have been explained. LAN is not a constant since the beginning of point 3) indicates: Where LANR is: That is, LAN is a factor that varies linearly with energy of excited electron. Figure 4 and 5 are contributed in initial post to be able to corroborate this linearity. It is also noted that sensitivity to variations in energy is high (Figure 5.B.) Many examples of atoms and atomic electron transition can be indicated where this relation of linearity between LAN and energy of excited electron can be corroborated with reference data (considering point 4) when atomic number increases) so is "just arbitrary curve fitting", rather a linearity, which all meet. An advantage is that also allows predicting energy values of excited electron for high n. If you want I can develop calculations made. Regards

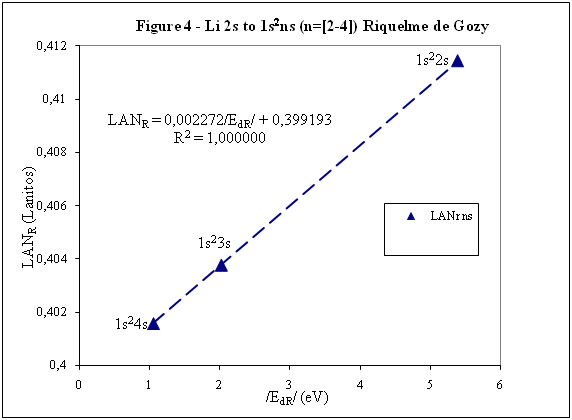
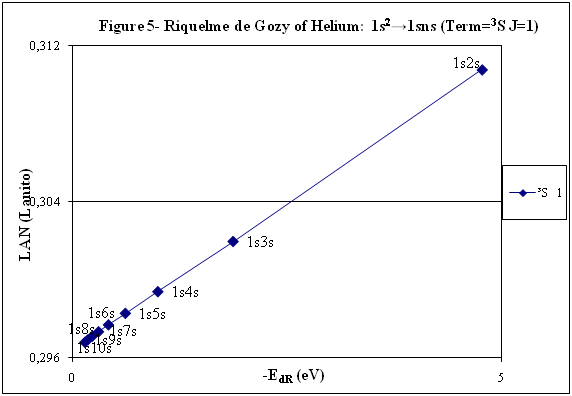
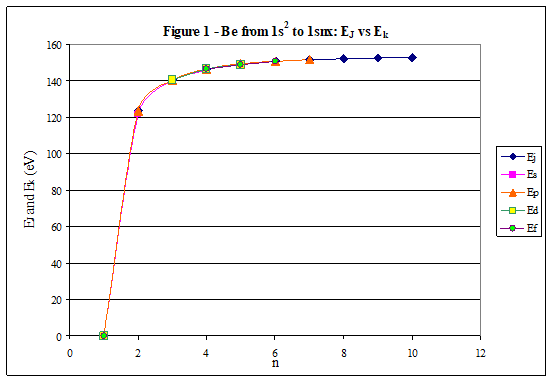
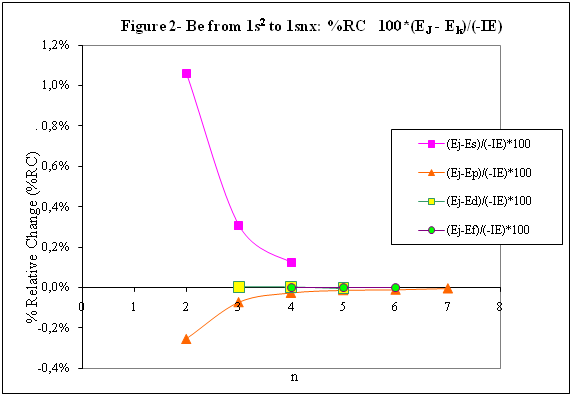
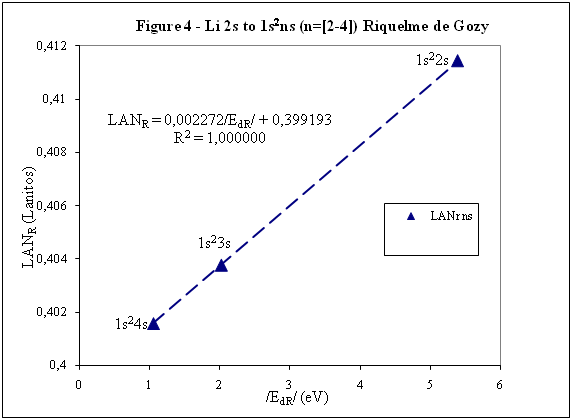
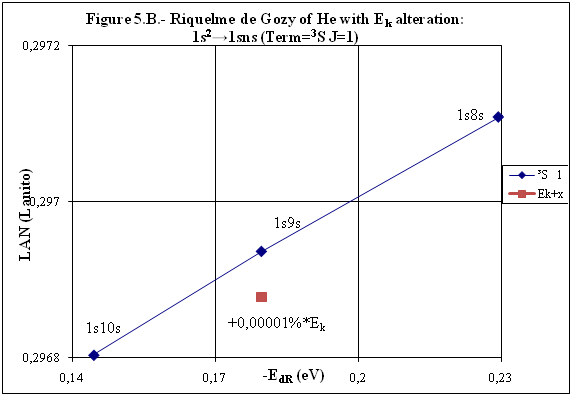
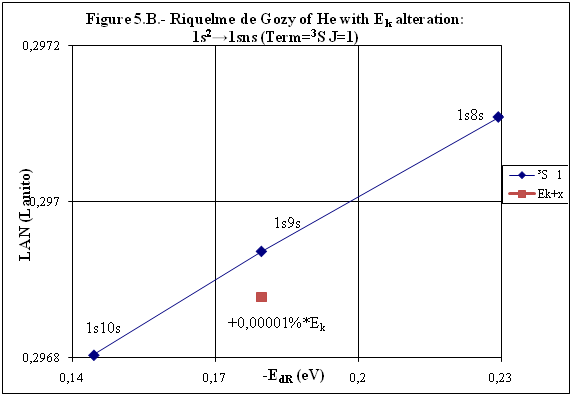
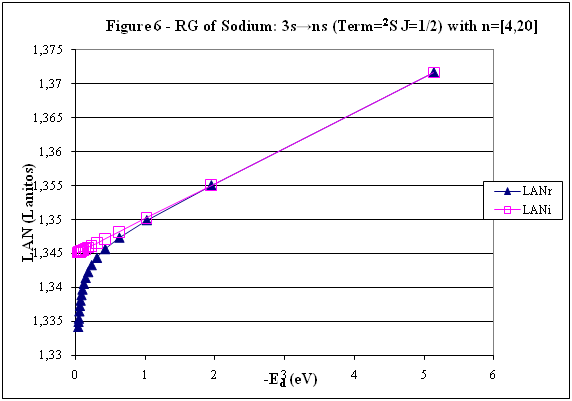
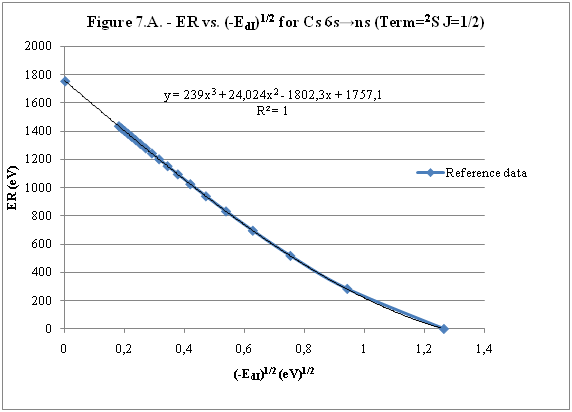
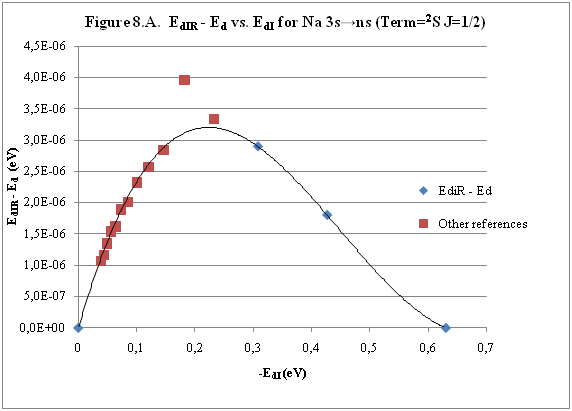
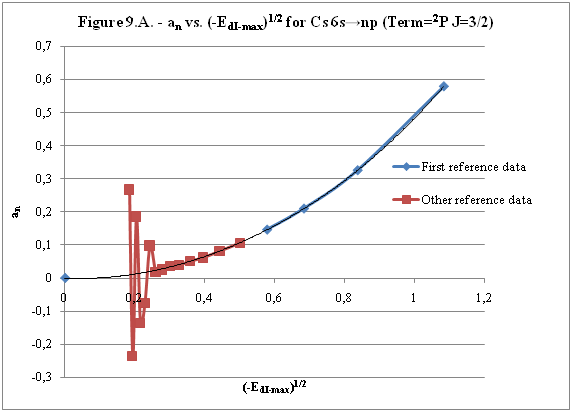
ABSTRACT Topic is centred in Relation of Riquelme de Gozy that is part of relations fulfilled by electrons excited (LAN Theory). Article exposes a new concept of excitation lines based on orbital quantum number and, after relativistic effect inclusion, progressively increases sensitivity in energetic values of electronic jumps to be able to predict said values and discern possible errors included in the references. KEYWORDS: Excited electron, Energy level, Relativistic effect, LAN, Relation of Riquelme de Gozy. SUMMARY 1) Central or Main Line Excited states of electron are born referenced to central line, always originating in Electronic Origin System (OES) of every atom: electron 1s (1) Ej (Jump energy in Central Line) Jumping energy to reach excited state in Central Line Ed (Excited state destiny energy) Destiny energy of excited state. IE (Ionization Energy) Ionization energy of excited electron zs (Start charge according to P46) Output charge of excited electron according to P46 Eo (1s OES Ionization energy) Electron ionization energy 1s zo (1s Origin charge according to P46) 1s electron charge according to P46 "P46 non-excited electronic extreme charge" provides charge for (1) very simply by subtracting directly one charge for each electron that reaches atom (Boron example: 1s electron zo=5, 1s2 zs=4, 2s zs=3, 2s2 zs=2 and 2p zs=1). Be III example is studied with jump from 1s2 (Term 1S; J=0) to 1snx and where x is s, p, d and f. First impression (Figure 1) is that there is, at first glance, overlap between excited states with reference data (Lines Es, Ep, Ed and Ef) and Central Line (Ej) Overlap is not such and there is a differential between lines of excited states with reference data and Central or Man Line and this differential is reduced as quantum numbers n and l are increased. 2) Serelles Secondary Line - LAN Factor LAN factor arises to create secondary lines through which electrons flow, increasing the destination n as a function of the excited state, and is solution to what is seen in point 1. LAN is included in (1) to create Serelles secondary lines where inclusion of the suffix s in EJ and Ed refers to Serelles Secondary Line (3). LAN can be estimated from reference data as LANR (4): 3) Riquelme de Gozy Relation LAN has a linearity relationship with destiny energy. Figure 4 represents LANR for two excited states and initial state not excited in the jump from Li I 1s22s to 1s2ns. Linearity is perfect for these first 3 points (P50 establishes that non-excited state is linear with excited ones for jumps ns → ns. In the rest of jumps, linearity is demonstrated exclusively with excited jumps since the LANR calculated with ionization energy is not linear with them). LAN sensitivity is high with small variations in energy and allows jump energy to be provided with high accuracy. This energies predictive fact can be realized through LAN equation (4) and Riquelme de Gozy relation (5). Development leads to grade three equation (6) where destiny n for which energy wants to be estimated is selected since the only unknown is ideal destiny energy or EdI (following linearity of Riquelme de Gozy Relation) EdI data already show a high concordance with the experimental ones and in most of the cases with those calculated or estimated in the references. 4) Relativistic excess of the electron 1s LAN equation must consider relativistic excess of 1s OES (origin electronic system).1s relativistic excess (1s ER) (7) is energy that there is of difference between theoretical value (-13.6056899 eV * Z2) and experimental value (Eo). (7) 1s ER = ERo(EdR→0)= EoT - Eo = -13.6056899 eV * Z2 - Eo Relativistic excess, as indicated in (7), tends to be eliminated when destiny energy tends to zero and therefore the electron is located outside nucleus influence. Therefore, when electron is far from the nucleus, electron sees 1s electron with theoretical energy (-13.6056899 eV * Z2) and as approaches, excited electron feels 1s electron with a higher energy (in absolute value) until becomes Eo (experimental ionization energy for 1s electron) when Riquelme de Gozy Relation is calculated.This relativistic effect can be ignored when relativistic Excess value is comparatively low to Eo. This fact occurs when atomic number (Z) is low as in lithium case previously seen or in helium example where linearity of Riquelme de Gozy relation is very good using (4) (Figure 5) Small deviations of experimental energy imply visible alterations with respect to linearity of Riquelme de Gozy relation. Energy jump to 1s9s is increased by 0.00001% and implies linearity modification observable by the naked eye (Figure 5.B.).This linearity situation is no longer as optimal when Z increases and curvature of Riquelme de Gozy relation is observed for Na I (Figure 6). Differences are low between reference energies and those calculated by linearity of Riquelme de Gozy without considering variation of relativistic excess because LAN variation is not high (consequence of fact that sodium atomic number is still relatively low) and LAN is high sensitivity parameter. Curvature is increased when atomic number is greater as can be appreciated in this same jump made for following alkaline metals (K, Rb and Cs) Relativistic Excess (ER) necessary to adjust the curvature is given by (8), where EdR and EdI are reference and ideal destiny energies respectively and where EDI is provided by extrapolation to n higher realized with Riquelme de Gozy relation (6): ER calculation (8) is represented as function of (-EdI)1/2 and approximate curvature with polynomial of degree 3 or 4 is obtained (Figure 7). Regression coefficients tend to 1 and ordinate at origin agrees with relativistic excess of origin electron 1s (7). This tendency can be corroborated with any atom and electronic jump. Further representations (as Figure 8, 9...) are used to adjust energy values and find reference data that can be considered as susceptible to error when committing discontinuities in said representations. Note Figure 8.A. n = 9 is approximately correct, but n = 10 show a deviation of ≈ 10-6 eV and consequently n=10 is reference data with possible error Note Figure 9.A. Cs 6s → np (2P J=3/2) where can be checked as most of reference data are correctly located in curve except for three points (n = 20 n = 22 and n = 24). These 3 n of the reference are those that have the least significant figures.