Jan Slowak

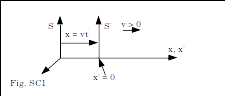
I really want to understand how Lorentz Transformations come about! I have analyzed the derivation of Lorentz Transformations (LT) in [3] The special and general theory of relativity; Albert Einstein; The first part; About the special theory of relativity; 2006; swedish [7] Modern Physics; Second edition; Randy Harris; Chapter 2; Special Relativity; 2008 I believe that the derivation in these two books is not self-consistent. Why? I explain below and would like help with this. Both in [3] and [7] one uses three special cases to derive LT. You start from two linear equations (I use my own notations to more easily refer to different parts of the derivation): LEx': x' = Ax + Bt LEt': t' = Cx + Dt To determine the constants A, B, C, D, three special cases are used: SC1: x' = 0, x = vt SC2: x = 0, x' = -vt' SC3: x' = ct', x = ct We look at the first one that I depict in Fig. SC1. SC1: x' = 0, x = vt My comment: At the time (t' > 0), an event occurs in the S'-origo (x' = 0). The literature states that the distance between S and S' is x = vt. I think this is wrong: It should be x = vt'. Why? S has no knowledge that the event occurred and where somewhere it happened! S' instead knows that the event occurred when its clock showed time t'. Then S' can definitely say that the distance between S and S' is vt'!

I do not want such discussions. I wrote at the beginning of this thread: I really want to understand how Lorentz Transformations work! I think I do not make a mistake in Fig. 4-06b, Fig. 4-07b. If you think I'm wrong then I want an explanation! Specifically, no deviation from the main subject. So: Where are the errors I make in the pictures Fig. 4-06b, Fig. 4-07b and how I describe the phenomenon?

I can also write in the same way as you: Note: you are obviously wrong, you just need to learn to accept that and then understand why. What are you doing? But I do not want to engage in such discussions. I wanted to talk about the derivation of Lorentz Transformations.

Where are the errors I make in the pictures Fig. 4-06b, Fig. 4-07b and how I describe the phenomenon? I do not ignore what you write. I read everything and think and answer. Refer to the pictures Fig. 4-06b, Fig. 4-07b and say where am I wrong.

Where are the errors I make in the pictures Fig. 4-06b, Fig. 4-07b and how I describe the phenomenon?

Thanks. I've watched the video before. So you cannot prove that I am wrong in the pictures Fig. 4-06, Fig. 4-07!

You jump between different pictures and do not logically follow our disclaimer. An event is denoted by E = (x, t) for S and E'= (x', t') for S'. In Fig. 4-05, it should be E '= (x', t '). But don't forget that E is identical to E '. Where are the errors I make in the pictures Fig. 4-06, Fig. 4-07 and how I describe the phenomenon?

If you mean your question At the same time in whose frame? then my answer is as follows: in S, this should be obvious. I write in my explanation of the picture Fig. 4-05: At the same time, an event, a light signal, occurs in the point Px. Px is in the reference system S (x refers to S, x' refers to S'). Once again: we talk about the pictures Fig. 4-06 and 4-07 (or Fig. 4-06b and 4-07b, in these are also S depicted). Can you be more specific and write what are the errors I do? What is incompatible with the first postulate?

From Wikipedia: 1) The special theory of relativity postulates that the speed of light in vacuum is constant equal to c for all observers in uniform relative motion. 2) All systems, where observers move at a constant speed, inertial systems, are equivalent and therefore the laws of physics must give the same results for all of them. I didn't want to complicate pictures unnecessarily. But in my description of Figs. 4-06 and 4-07 one could read what applies to S' and what applies to S. I attach copies of these two pictures where I draw S in the point P0.

Fig. 4-06, Fig. 4-07: When S' in its motion is in the S-origo, when t = t' = 0, then the event in S arises at a distance x from the S-origo. You can use the same postulates used in the literature: [3] The special and general theory of relativity; Albert Einstein; The first part; About the special theory of relativity; 2006; swedish [7] Modern Physics; Second edition; Randy Harris; Chapter 2; Special Relativity; 2008 Fig. 4-06, Fig. 4-07: Can you be more specific and write what are the errors I do? Please check my answers to Ghideon and swansont.

I do not mix with reference systems. I use them in the same way as in [3] The special and general theory of relativity; Albert Einstein; The first part; About the special theory of relativity; 2006; swedish [7] Modern Physics; Second edition; Randy Harris; Chapter 2; Special Relativity; 2008 You make measurements in a reference system and equate the result with the variable from the other. For example: x = Ax' + Bt'; LTx': x' = (x – vt)γ; LTt': t' = (t – vx/c2)γ What is the problem? Where are the errors I make in the pictures Fig. 4-06, Fig. 4-07 and how I describe the phenomenon? We have only one reality, but each of the observers expresses and describes their measurements with their own variables. We have an event somewhere on the x-axis of S. S denotes the event with E = (x, t). S' denotes the event with E' = (x', t'). But for both reference systems, it's all about one and the same event! What is the problem with this? I ask you the same question that I asked to swansont. Where are the errors I make in the pictures Fig. 4-06, Fig. 4-07 and how I describe the phenomenon? Be specific, please.

It is not a similar problem, but it is exactly the same problem with clearer explanations and pictures. I was going to help Ghideon move on. The sum of the two lengths for S' is vt' + ct' and it is the same length as x in S. We have two reference systems but we have only one reality!

Another explanation for the same phenomenon. A reference system S' moves on the x-axis to the right at a constant speed v > 0. When S' passes the point P0, its clock is reset, t' = 0. At the same time, an event, a light signal, occurs in the point Px. Px is at a distance x from the point P0. While the light signal moves towards S', S' moves to the right. When the light signal reaches S', two distances occur on the x-axis. Distance [P0, S'] and distance [S', Px]. The length of these two distances is: Distance [P0, S'] = vt' Distance [S', Px] = ct' Then we have the following relationship: x = vt'+ ct'. Is this right?

When I describe a physical phenomenon, make a mathematical model of it, presents my ideas, arguments, then I do not want to deviate from the main track. It's not possible! I present something, ask if I am right or wrong, then I want either an approval, Yes, or a No, but then you have to counter-argument. It should not be more difficult than that!

This is no answer. If you answer NO, you must counter-argument.