Kuyukov Vitaly

In multidimensional models, the behavior of the string and membrane is considered. The membrane is not suitable for the role of quantum particles. You can consider information membranes based on the Fisher metric. B.pdf

The nature of the time is counterdiced. On the one hand, the disappearance of time in Wheeler's equation. On the other hand, Penrose talks about the reality of time. There is another definition, in the form of a holographic hypothesis $$ t=\frac{Gh}{c^2} \int \frac{dS}{r} $$22.pdf

Solution for space-time metric $$ S = \frac{dV}{dt}=g_{ik}^|g_{ik}V+ π_{ik}g_{ik}V $$

Thickness axons ( L ) in the neural network limits speed signal transmission $$ v = \frac{Gh}{c^2} \frac{1}{L^2} $$

I fully agree with the concept of gravity based on quantum theory. I offer you your point of view. In general, my work is based on a Cotton flow for a gauge field. Let's see further. The theory of everything is mainly associated with the general theory of relativity and the standard model. On the one hand, the equivalence principle and on the other hand the gauge principle. The two principles are completely opposite to use, one for space-time geometry, the other for quantum fields. For the union is looking for a way called quantum gravity. Canonical quantization of gravity is called Wheeler equation. However, there are difficulties, lack of time and the inability to combine with quantum fields. The equation is purely wave and geometric. All fundamental laws are usually symmetrical in time, even the gauge fields of the standard model are reversible. However, in the real world, time has a strict direction to the future. This is another problem. We believe that the quantum gravity equation is not linear in time. This trip is supported by Roger Penrose and Lee Smolin. At the fundamental level on the scale of the Planck, time is real and has an arrow due to the nonlinearity of the quantum gravity equation. In the recent work we generalized the concept of Cotton Flow is not in the form of a metric, but in the form of a gauge field. This equation describes the behavior of nonlinear in the time of the gauge field on the scale of the Planck. $$ \frac{\partial S}{\partial t}= kC $$ $$ A_{i}=\partial_{i} S$$ $$ K_{in}=\partial_{i} A_{n}+A_{i}A_{n}$$ $$ C=e^{inj}C_{inj}=e^{inj}\partial_{i} K_{nj}$$ $$ k=\frac{Gh}{c^2}$$ In this equation for the gauge field, the solution itself is interesting in the form of finding the local phase of the wave function. $$ S=S(x,y,z,t) $$ $$ \psi=e^{iS} $$ The general solution of the nonlinear equation in time will be $$ S=k\int Cdt + \int A^{i}dx_{i} + f(x,y,z,t)$$ Thus, a series of compounds and splitting of cylindrical pipelines together creates a topological structure of a gauge field as a web or in the form of neural networks on the scale of the Planck. The neural network of the gauge field is subject to a nonlinear equation so that it develops in the future and expanded. This neural network is dynamic in time. Consider some solutions for special cases. Gravity and gauge field the scale Planck. In this chapter, we will show how the gauge neural network on the scale of the Planck creates gravity on a large scale, where there is a classic world. Consider the equation of the neural field. We make an assumption that on a large scale curvature of the field due to the least $$\frac{\partial S}{\partial t}=kC=e^{inj} A_{i}\partial_{n} A_{j}$$ Can be determined in the form of a function from the local phase. Decision in the form of a reduction in the rule of differentiation of derivatives $$\frac{\partial S}{\partial t}=ke^{inj} \partial_{n}S \partial_{n}\partial_{j}S $$ Decision in the form of a reduction in the rule of differentiation of derivatives $$v_{i}=\frac{dx_{i}}{dt}=ke^{inj} \partial_{n}\partial_{j}S $$ As can be seen, there is some idea of the speed of movement, that is, the initial concept of kinematics. We introduce the transverse surface in the form of an area $$ dF_{i}=e^{inj} dx_{n}dx_{j} $$ As a result, an additional solution for the local phase of the gauge neural field will be $$ S=k\int Cdt + \int A^{i}dx_{i} +\frac{1}{k} \int v_{i}dF^{i}+ f(x,y,z,t)$$ Moreover, now we will see the appearance of gravity. Consider the kinematic action for the gauge neural network $$ S=\frac{1}{k} \int v_{i}dF^{i}$$ Let the reference system accelerates $$ a_{i}=\int v_{i}dt $$ Then the action will be accelerated $$ S=\frac{1}{k} \int a_{i}dF^{i}dt $$ This definition of action in the form of a function of time, besides, if there is matter in this gauge neural network, the overall action will be $$ S=\frac{1}{k} \int a_{i}dF^{i}dt+ \int Mc^2dt$$ As a result, when variations are obtained, the Gauss theorem is obtained for the source of the gravitational field. $$ \int a_{i}dF^{i} =-4\pi G M$$ Thus, we have the Poisson equation for the gravitational field, which is true in the classical world, when taking into account the signal transmission limit at the speed of light the theory of gravity is described by the general theory relativity. Gravity is a curvature of space-time. On the other hand, our theory also describes gravity as a dynamic state of the gauge neural network. Thus, the source quantum state of space-time is like a neural network on a scale Planck based on a gauge principle. In fact, quantum gravity is a non-linear quantum field theory on the scale of the Planck. WG.pdf

Renormalization problem for two-dimensional objects in string theory. Membranes are unstable at the quantum level. I propose to consider membranes as information structures, and not just the geometry of surfaces. It is based on information metric Fisher. Mathematical analysis based on the holographic principle allows one to determine the flow formula for a quantum membrane. This formula is similar to Gauss theorem for the flow of a gravitational field. This removes instability and allows membranes to be viewed as fundamental units of information. B.pdf

The Bousso limit is a holographic hypothesis, the maximum amount of information on the border of the light sphere is equal to its surface area. I = A / 4 I propose to generalize this result for all cases of motion, for fixed and light holographic screens. Information equals speed times screen area I = v A / 4 This result is interesting because it gives a different interpretation of the velocity addition theorem based on the Fisher metric 24.pdf

You are absolutely right. The vacuum energy near the GUT makes the main contribution to the braid topology (monopole mass). There are two solutions 1. The super scalar Higgs field at the GUT scale affects the braid topology Ф ~ A ~ B ~ C 2 Braid size increases to GUT scale due to cosmological inflation I'm interested in the second option.

The model completely dispenses with supersymmetry, instead reducing the number of components and parameters for the rigidity of the theory.

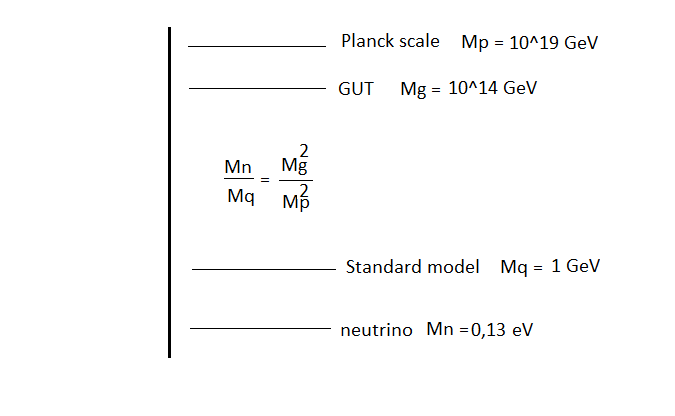
Proposed on the basis of the model preons, I obtained an empirical formula for all energy scales (neutrinos, standard model, theories of great unification, planck scale). Mn / Mq = (Mg / Mp) 2 Mn = 0.13 eV Mq = 1 GeV Mg = 10^14 GeV Mp = 10^19 GeV The great thing is the relationship between these scales based on this one formula. E = 1 / Mp2 ∫dA dB dC Where A, B, C are parameters of the braid topology in the form of gravitational field lines. This formula shows that the energy of the particles is a combination of the field fluxes A, B, C in the spit topology. In general, the uniform dimensions of the braids are the same A = B = C = 1 / L Then the energy will be E = 1/Mp2 ∫dA dB dC = Lp2 / L3 = 10 ^ -70 / 10 ^ -84 = 1 GeV At a proton energy E = 1 GeV, the size of the topological structure is L = 10 ^ - 28 m, which corresponds to the scale of the theory of great unification (the mass of the monopole is 10 ^ 14 GeV). vb.pdf

Some aspects of special relativity can be defined through the geometry of entanglement, such quantities as holographic screens, speed, time. The main focus is on the entangled empty space entropy as the basis for the emergence of holography in special relativity sp.pdf

There is an interesting fact, if the de Broglie wavelength is equal to the Planck length, then the momentum is determined on the Planck scale L= 10 {-35} m p = m v = h k = h / L = 60 ( kg m/s) A person lives with such an momentum (60 kg, 1 m / s) , intelligent creature. I think this is not a simple coincidence, on the Planck scale the concept of space-time is replaced by quantum gravity, moreover, the quantum theory is modified (generalized uncertainty principle). This means that the wave properties on the Planck scale should disappear (the many-worlds interpretation disappears, a single self remains), the border between the quantum world and the classical world passes on a human scale. Moreover, I am formulating the idea of a wave filter. Any sentient being must have momentum in the area of the Planck scale (not less than this value). If the momentum is less, then wave properties prevail, then the mind splits into many worlds branches, a single rational self will not arise. Human momentum fits perfectly into the Planck scale (on the border between the quantum and the classical world). Fermi paradox, where are the civilizations in the galaxy. Quantum gravity responds, an intelligent creature exists with momentum in the region of the Planck scale, where the wave properties of the body disappear. This is a very small detection range. This is a wave filter.

Tighter restrictions on supersymmetry (string theory) at the detector https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=newssearch&cd=&cad=rja&uact=8&ved=0ahUKEwjO8JKP9qzrAhVVmMMKHRndCooQxfQBCC0wAA&url=https%3A%2F%2Fphys.org%2Fnews%2F2020-08-heavy-higgs-bosons-tau-leptons.html&usg=AOvVaw1RyKbcd9pPiTRo0OV2IZXl It looks like it smells like a grave for string theory (and higher dimensional models).

The best idea in quantum gravity is the holographic principle. Holographic equivalence between gravity in volume and quantum theory on the surface (AdS / CFT). For example, a black hole encodes quantum information on the horizon. In this theory, matrix objects are more fundamental than the strings themselves. Here a topological formula for calculating the energy of a matrix object is obtained (equivalent to the Gauss theorem for gravitational mass). More details here. B.pdf

After all, string theory was originally a boson theory. Fermions were obtained only due to the expansion of supersymmetry. 1.pdf