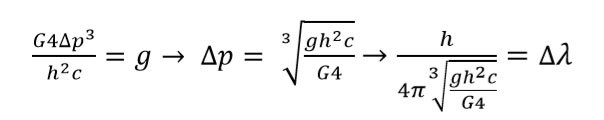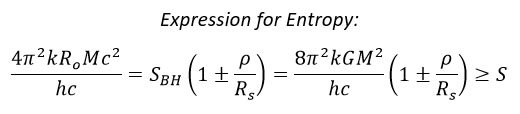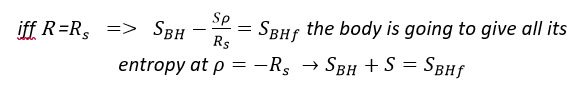RedShiftam

An average human brain in rest relative to me has a mass of 1.5 kg and a volume of 1260 cm3. If the brain is approximated by a sphere, then the radius will be 6.7 cm.The informational Bekenstein bound will be about 2.6×10 42 bits and represents the maximal information needed to perfectly recreate an average human brain. If this brain start moving relative to me with high speed, because of the length contraction of the brain and its relativistic mass the formula for the upper limit of information will stay constant. Because all correction terms of gamma in the formula will cancels out.

Is it possible to observe a region of space that has information density greater than what the Bekenstein Bound will allow when length contraction is involved? I.e. An object travels through the region of space close enough to the speed of light relative to the observer to appear more information dense than what the limit would permit. Or does it only make sense to calculate the Bekenstein Bound based off of an object's rest frame? I've copied it this question from another place because it is the same thing that I wanted to ask. I didn't see any replies so i decide to post it here.

Maybe the best way to understand and to have a some mental picture for what is time is the second law of thermodynamics. Consider that time maybe is not fundamental. Time measure change and if you are traveling only thru the time dimension it's a measure how you as a system change. All the stuff you are made of are little clocks and honestly i think that we can't not move only in the time dimension. We are made of form many subsystems and if the main system don't move that doesn't mean that the subsystems doesn't move. They are moving relative to each other. If i imagine a thing which doesn't have subsystems and a freeze that thing what your thing is going to happen? I think that the concept of time disappears!

Thanks a lot man!

Can somebody share an a articles or something related with this topic. I want to understand well the main problem (the root and the details) and why it is so difficult. I've come across many videos and news that give you some kind of metaphorical picture (made for the public), which in some cases is quite misleading. I don't need the approaches (string theory, loop quantum gravity), i need just the problem! Thank you for your time!

My original thought was if I start to constrain a particle in less and less space, is it that going to change the gravitational force of that particle, which is acting on a object? So that more uncertainty in momentum will correspond to more G-force. Apparently my thought experiment is not well constructed!

Now, as you say it, I think you are right that I confused them. I don't know what you mean by that? This is the momentum formula h/wavelength=p!

G is the gravitational constant. I think is clear that. Maybe i don't understand your question. You can see above and see from where it comes. Photons are also a type of elementary particle.

Momentum of a photon is h/wavelength! L/n =wavelength (this n doesn't mean the number of a particles). So the formula is not wrong!

In this case I do not need two or more objects! In this formula I use frequency as a source of energy. Derivation is logical. This formula It's just the end result. Apparently I had to put the whole line. I'm sorry fo that! The walls of the box may be visualised as regions of space with an infinitely large potential energy. Conversely, the interior of the box has a constant, zero potential energy.This means that no forces act upon the particle inside the box and it can move freely in that region.

Let’s we imagine a particle that is in a box and it hits the walls of the box with a certain frequency. Let's say that the energy of the box comes from the frequency with which the particle hits the walls. If we start to shrink, the box frequency will become bigger and the energy of the box will rise. But the smaller the box, the better we will know where the particle is, from where it follows that the uncertainty in momentum is going to get bigger. On the other hand, if we have a test object close enough to the box, this object will experience a greater gravitational pull from the box. I made a derivation using the Newtonian laws of gravity and I got this formula. So where am wrong?

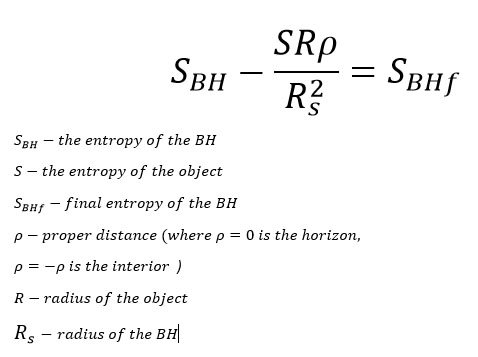
I recently tried to imagine a different kind of BH. For Ex.: the entropy of the BH grows gradually as the body enters the interior. But there is a problem with this formula, if the object is small, it will give all its entropy much after the center of the BH. So if we decide that the object has radius equal of the BH is going to be better. This is just a quick thought and nothing more!

I read the article and the conclusion is that if we want information not to be lost one of the ways is to say that the late radiation is entangled with the early radiation. As far as I understand the whole problem is to find a way to preserve the entanglement (between the particles). Honestly, I don't like very much this idea that the particle into the black hole is connected through a wormhole with the particle out of the hole.

The virtual pairs of particles are also entangled. Hawking radiation is gained by particle–antiparticle radiation emitted from just beyond the event horizon. This radiation does not come directly from the black hole itself, but rather is a result of virtual (entangled) particles being "boosted" by the black hole's gravitation into becoming real particles. The positive one (Hawking radiation) escapes but the negative one lowers the mass of the hole. So if the black hole evaporates over time why does the late radiation have to be highly entangled with the early radiation? They are already entangled with their partners who are in the black hole's interior.

I am a bit confused. There are virtual particles in the space, that are entangled and thanks to that the space is not breaking apart. According to the thought experiment (28min to 40min), we create from some material a pair of particles that are entangled(Bell pairs). Then we divide them, and we make from them two black holes. These black holes are also entangled. So if the holes are made of some material and not from the virtual particles, it follows that the material from which the black holes are made can not be entangled with the virtual particles that are outside the event horizon. So the virtual particles, outside event horizon must remain entangled with those who find themselves in the black hole's interior. On the other hand, if the black holes are made of the virtual particles, then I understand why this monogamy problem comes out. Lecture :

Ok and why is that? Clearly the formula doesn't say that. You can put any value for a radius.I mean that there are so many possible configurations of Energy and radius in the formula. My point is that the Bekenstein Bound formula must be written in some other way in which you can see the conservation of the entropy of a black hole.

Yeah i know that! But the Bekenstein Bound doesn't tell you this. I mean the Schwarzschild radius is a special case. The mass still collapses. I thing that the formula must be writen in some other way in wich it keeps the entropy a constant even after the Schwarzschild radius and preserv all other cases.

Hi I'm writing in the hope that someone can help me to understand my confusion on a question. It's about the upper limit of entropy S or information I, which can be contained in a limited region of space that has a finite amount of energy. I looked at the formula and thought that if my energy is constant (say it is a one solar mass) and the radius, for example, starts approaching the zero, entropy it will be quite small. At some point, when the radius becomes equal to the Schwarzschild Radius, the object will become a black hole which it has a certain entropy. But In General Theory of Relativity mass will continue to shrink into a smaller and smaller region, which means smaller and smaller entropy. But it is known that the black hole has defined entropy, as long as something does not come into it. In this line of thought, does this mean that after we passes the Schwarzschild Radius, the Bekenstein bound is not a solution for the BH interior? Or everything is fine the value for the entropy is preserved and all we need is а better understanding for what is happening with the mass after the Schwarzschild Radius? Thank you for your attention! Greetings!